2025年中考数学几何压轴题解题方法突破--等腰三角形与中点(含解析)
文档属性
| 名称 | 2025年中考数学几何压轴题解题方法突破--等腰三角形与中点(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 129.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 14:14:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
等腰三角形与中点
【题目】
如图1所示,在△ABC中,AB=AC,∠BAC=α,点 D在边BC上,以点A 为中心,将线段AD顺时针旋转α得到线段AE,连接 BE.
(1)求证:BA 平分∠EBC.
(2)连接DE交AB 于点F,过点C作CG∥AB,交ED的延长线于点G.补全图形,用等式表示线段 EF 与DG 之间的数量关系,并证明.
【读题】
本题属于等腰三角形和旋转变换的类型.(1)很简单,由等腰和全等两个条件即可证得结论成立.(2)考查两条线段的数量关系,先画图,再构造全等三角形.分析图形如图2~7所示.
【分析】
(1)由△ABC为等腰三角形,可得∠ABC=∠ACB.再证△ABE≌△ACD,可得∠ABE=∠ACD.于是可得结论成立.
(2)可如图2所示补全图形.
由几何直观可得EF=DG,并考虑构造全等三角形.考虑到第一问的结论,可以采用角平分线的构造模型进行分析.
方法一:
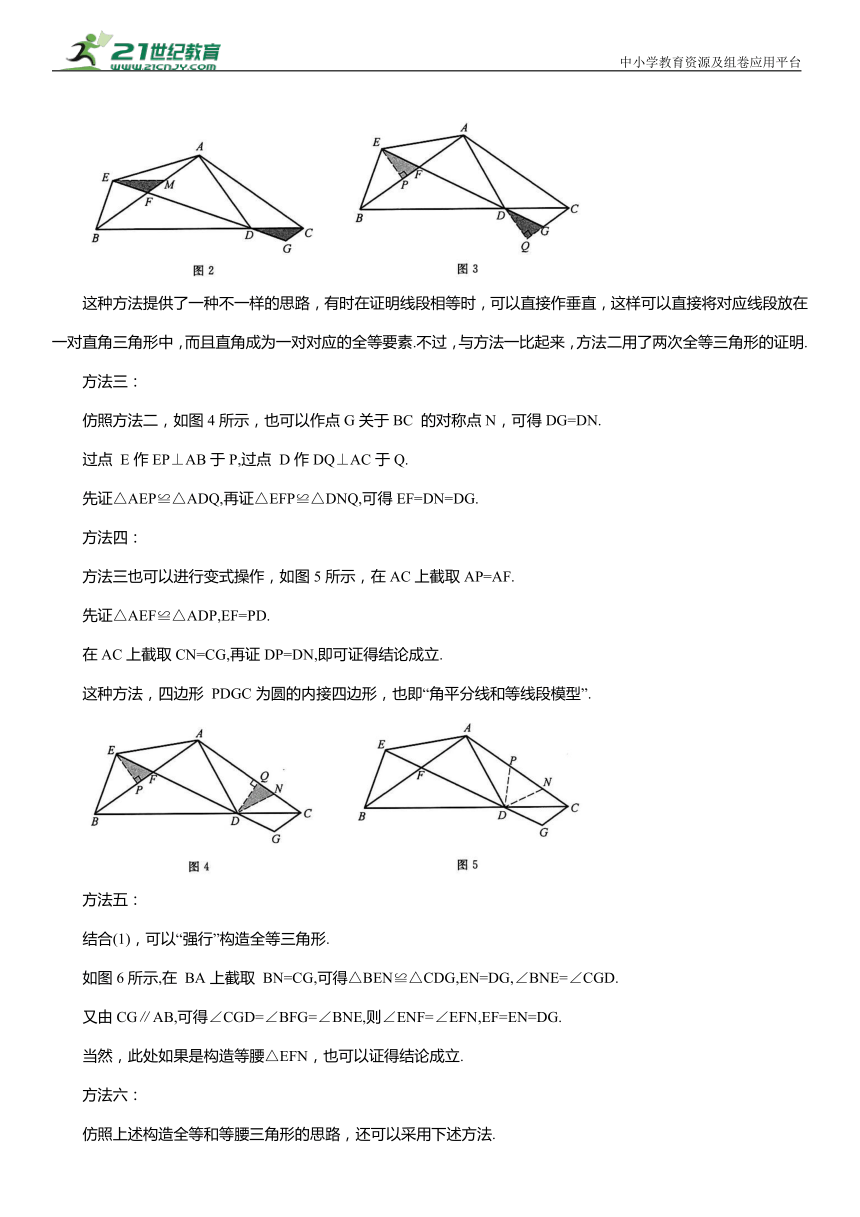
如图2所示,过点 E作EM∥BC,可得△BEM为等腰三角形,BE=EM=CD.
由CG∥AB,可得∠DCG=∠ABC=∠FME,∠CGD=∠BFG=∠EFM.
于是可得△EFM≌△DGC,EF=DG.
本题还有其他方法,上述方法是较为直接的一种.
方法二:
如图3所示,过点 E作EP⊥AB于P,过点 D作DQ⊥CG于Q.
先证△BEP≌△CDQ,再证△EFP≌△DGQ,可得结论成立.
这种方法提供了一种不一样的思路,有时在证明线段相等时,可以直接作垂直,这样可以直接将对应线段放在一对直角三角形中,而且直角成为一对对应的全等要素.不过,与方法一比起来,方法二用了两次全等三角形的证明.
方法三:
仿照方法二,如图4所示,也可以作点G关于BC 的对称点N,可得DG=DN.
过点 E作EP⊥AB于P,过点 D作DQ⊥AC于Q.
先证△AEP≌△ADQ,再证△EFP≌△DNQ,可得EF=DN=DG.
方法四:
方法三也可以进行变式操作,如图5所示,在AC上截取AP=AF.
先证△AEF≌△ADP,EF=PD.
在AC上截取CN=CG,再证DP=DN,即可证得结论成立.
这种方法,四边形 PDGC为圆的内接四边形,也即“角平分线和等线段模型”.
方法五:
结合(1),可以“强行”构造全等三角形.
如图6所示,在 BA上截取 BN=CG,可得△BEN≌△CDG,EN=DG,∠BNE=∠CGD.
又由CG∥AB,可得∠CGD=∠BFG=∠BNE,则∠ENF=∠EFN,EF=EN=DG.
当然,此处如果是构造等腰△EFN,也可以证得结论成立.
方法六:
仿照上述构造全等和等腰三角形的思路,还可以采用下述方法.
如图7所示,延长CG 至 N 使CN=BF,可证△BEF≌△CDN,EF=DN,∠BFE=∠CND.
又由CN∥AB,可得∠AFG=∠FGN,于是∠BFE=∠AFG=∠FGN=∠CND,DG=DN=EF.
【答案】
(1)证明:因为将线段AD顺时针旋转α得到线段AE,所以∠EAD=α,AD=AE
因为∠BAC=α,
所以∠BAC=∠EAD
∠BAC-∠BAD=∠EAD-∠BAD
∠DAC=∠EAB
在△ACD 和△ABE中
△ACD≌△ABE (SAS)
∠ABE=∠C
因为AB=AC,所以
∠ABC=∠C
∠ABE=∠ABC
因此 BA 平分∠EBC.
(2)补全图形如图8所示,EF=DG.理由如下.
证明:在AB上取一点M,使得 BM=CG,连接EM.
因为CG∥AB,所以
∠ABC=∠DCG,∠BFG=∠CGD
∠EBM=∠DCG
由(1)知△ACD≌△ABE,因此
EB=CD
在△EBM和△DCG中
△EBM≌△DCG (SAS)
EM=DG,∠EMB=∠DGC
因为
∠EMB+∠EMF=180°
∠EFM+∠DFM=180°
∠EMB=∠DGC=∠DFM
所以∠EMF=∠EFM
EM=EF
EF=DG
【反思】
1.本题的基本模型是等腰三角形的“手拉手”模型.
2.做题时注意问题之间的衔接和铺垫.前一问的结果,可能是后一问全等三角形的一个条件,或者是过渡的条件.
3.线段相等,最朴素的思想是构造相应线段所在的全等三角形,也可以通过中间量构造全等三角形.
等腰三角形与中点
【题目】
如图1所示,在△ABC中,AB=AC,∠BAC=α,点 D在边BC上,以点A 为中心,将线段AD顺时针旋转α得到线段AE,连接 BE.
(1)求证:BA 平分∠EBC.
(2)连接DE交AB 于点F,过点C作CG∥AB,交ED的延长线于点G.补全图形,用等式表示线段 EF 与DG 之间的数量关系,并证明.
【读题】
本题属于等腰三角形和旋转变换的类型.(1)很简单,由等腰和全等两个条件即可证得结论成立.(2)考查两条线段的数量关系,先画图,再构造全等三角形.分析图形如图2~7所示.
【分析】
(1)由△ABC为等腰三角形,可得∠ABC=∠ACB.再证△ABE≌△ACD,可得∠ABE=∠ACD.于是可得结论成立.
(2)可如图2所示补全图形.
由几何直观可得EF=DG,并考虑构造全等三角形.考虑到第一问的结论,可以采用角平分线的构造模型进行分析.
方法一:
如图2所示,过点 E作EM∥BC,可得△BEM为等腰三角形,BE=EM=CD.
由CG∥AB,可得∠DCG=∠ABC=∠FME,∠CGD=∠BFG=∠EFM.
于是可得△EFM≌△DGC,EF=DG.
本题还有其他方法,上述方法是较为直接的一种.
方法二:
如图3所示,过点 E作EP⊥AB于P,过点 D作DQ⊥CG于Q.
先证△BEP≌△CDQ,再证△EFP≌△DGQ,可得结论成立.
这种方法提供了一种不一样的思路,有时在证明线段相等时,可以直接作垂直,这样可以直接将对应线段放在一对直角三角形中,而且直角成为一对对应的全等要素.不过,与方法一比起来,方法二用了两次全等三角形的证明.
方法三:
仿照方法二,如图4所示,也可以作点G关于BC 的对称点N,可得DG=DN.
过点 E作EP⊥AB于P,过点 D作DQ⊥AC于Q.
先证△AEP≌△ADQ,再证△EFP≌△DNQ,可得EF=DN=DG.
方法四:
方法三也可以进行变式操作,如图5所示,在AC上截取AP=AF.
先证△AEF≌△ADP,EF=PD.
在AC上截取CN=CG,再证DP=DN,即可证得结论成立.
这种方法,四边形 PDGC为圆的内接四边形,也即“角平分线和等线段模型”.
方法五:
结合(1),可以“强行”构造全等三角形.
如图6所示,在 BA上截取 BN=CG,可得△BEN≌△CDG,EN=DG,∠BNE=∠CGD.
又由CG∥AB,可得∠CGD=∠BFG=∠BNE,则∠ENF=∠EFN,EF=EN=DG.
当然,此处如果是构造等腰△EFN,也可以证得结论成立.
方法六:
仿照上述构造全等和等腰三角形的思路,还可以采用下述方法.
如图7所示,延长CG 至 N 使CN=BF,可证△BEF≌△CDN,EF=DN,∠BFE=∠CND.
又由CN∥AB,可得∠AFG=∠FGN,于是∠BFE=∠AFG=∠FGN=∠CND,DG=DN=EF.
【答案】
(1)证明:因为将线段AD顺时针旋转α得到线段AE,所以∠EAD=α,AD=AE
因为∠BAC=α,
所以∠BAC=∠EAD
∠BAC-∠BAD=∠EAD-∠BAD
∠DAC=∠EAB
在△ACD 和△ABE中
△ACD≌△ABE (SAS)
∠ABE=∠C
因为AB=AC,所以
∠ABC=∠C
∠ABE=∠ABC
因此 BA 平分∠EBC.
(2)补全图形如图8所示,EF=DG.理由如下.
证明:在AB上取一点M,使得 BM=CG,连接EM.
因为CG∥AB,所以
∠ABC=∠DCG,∠BFG=∠CGD
∠EBM=∠DCG
由(1)知△ACD≌△ABE,因此
EB=CD
在△EBM和△DCG中
△EBM≌△DCG (SAS)
EM=DG,∠EMB=∠DGC
因为
∠EMB+∠EMF=180°
∠EFM+∠DFM=180°
∠EMB=∠DGC=∠DFM
所以∠EMF=∠EFM
EM=EF
EF=DG
【反思】
1.本题的基本模型是等腰三角形的“手拉手”模型.
2.做题时注意问题之间的衔接和铺垫.前一问的结果,可能是后一问全等三角形的一个条件,或者是过渡的条件.
3.线段相等,最朴素的思想是构造相应线段所在的全等三角形,也可以通过中间量构造全等三角形.
同课章节目录
