2025年中考数学二轮专题复习 等腰三角形的存在性问题 专项练习 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 等腰三角形的存在性问题 专项练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 14:18:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
等腰三角形的存在性问题
1. 如图1,抛物线 经过点A(-2,5),与x轴相交于点B(-1,0),C(3,0)两点.
(1) 求抛物线的函数表达式;
(2) 点D 在抛物线的对称轴上,且位于x轴的上方,将△BCD 沿直线BD 翻折得到△BC'D,若点C'恰好落在抛物线的对称轴上,求点 C'和点D 的坐标;
(3) 设P 是抛物线上位于对称轴右侧的一点,点Q 在抛物线的对称轴上,当△CPQ 为等边三角形时,求直线 BP 的函数表达式.
2. 如图1,抛物线与 x 轴交于A、B两点,与y 轴交于点C(0,—2),点A 的坐标是(2,0), P 为抛物线上的一个动点,过点 P 作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.
(1)求抛物线的函数表达式;
(2) 若点 P 在第二象限内,且 求△PBE 的面积;
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD 为腰的等腰三角形 若存在,求出点 M 的坐标;若不存在,说明理由.
3如图1,矩形ABCD中,AB=6,BC=8,P、E分别是线段AC、BC上 A的点,四边形 PEFD 是矩形,连结CF.
(1) 若△PCD 为等腰三角形,求 AP 的长;
(2)若 求CF 的长.
4. 抛物线L: 经过点A(0,1),与它的对称轴直线x=1交于点 B.
(1) 直接写出抛物线L 的解析式;
(2)如图1,过定点的直线y= kx-k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k 的值;
(3)如图2,将抛物线L 向上平移m(m>0)个单位长度得到抛物线L ,抛物线L 与y轴交于点C,过点C作y轴的垂线交抛物线L 于另一点D. F为抛物线L 的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF 相似,并且符合条件的点P恰有2个,求m的值及相应点P 的坐标.
思路点拨
1. 第(2)题探究定点的方法,可以把解析式的中含k的项提取k,就可以看到当x=1时,不论k 为何值,y的值都为4.
2. 探究得到的定点Q 也在对称轴上,这样求不规则△BMN 的面积就可以割补了.
3. 第(3)题恰有2个点 P 的意义,就是∠DPF 等于90°只存在一种情况.
5如图1,在半径为2的扇形AOB中,∠AOB =90°,点C 在半径OB 上,AC 的垂直平分线交OA 于点D,交弧AB 于点E,联结BE、CD.
(1) 若C 是半径OB 中点,求∠OCD 的正弦值;
(2) 若E 是弧AB 的中点,求证:
(3) 联结CE,当△DCE 是以CD 为腰的等腰三角形时,求CD 的长.
6如图1,已知在平面直角坐标系中,抛物线. 与x轴交于点 A 和点B(1,0),与y轴相交于点C(0,3).
(1) 求抛物线的解析式和顶点 D 的坐标;
(2)求证:∠DAB=∠ACB;
(3) 点Q 在抛物线上,且△ADQ 是以AD 为底的等腰三角形,求点Q的坐标.
7如图1,抛物线 与x轴交于A、B两点(点A 在点B 的左侧),与y轴交于点C,连接AC、BC.点P 是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为M, PM交BC于点Q,过点P作PE∥AC交x轴于点E,交 BC 于点F.
(1)求A、B、C三点的坐标;
(2) 试探究在点 P 运动的过程中,是否存在这样的点 Q,使得以A、C、Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;
(3) 请用含 m 的代数式表示线段QF 的长,并求出m 为何值时QF 有最大值.
8如图1,在平面直角坐标系中,已知点A 的坐标为(3,1),点B 的坐标为(6,5),点C 的坐标为(0,5),某二次函数的图像经过A、B、C三点.
(1) 求这个二次函数的解析式;
(2)假如点Q在该二次函数图像的对称轴上,且△ACQ 是等腰三角形,请直接写出点 Q 的坐标;
(3) 如果点 P 在(1)中求出的二次函数的图像上,且 求∠PCB 的正弦值.
专题直击
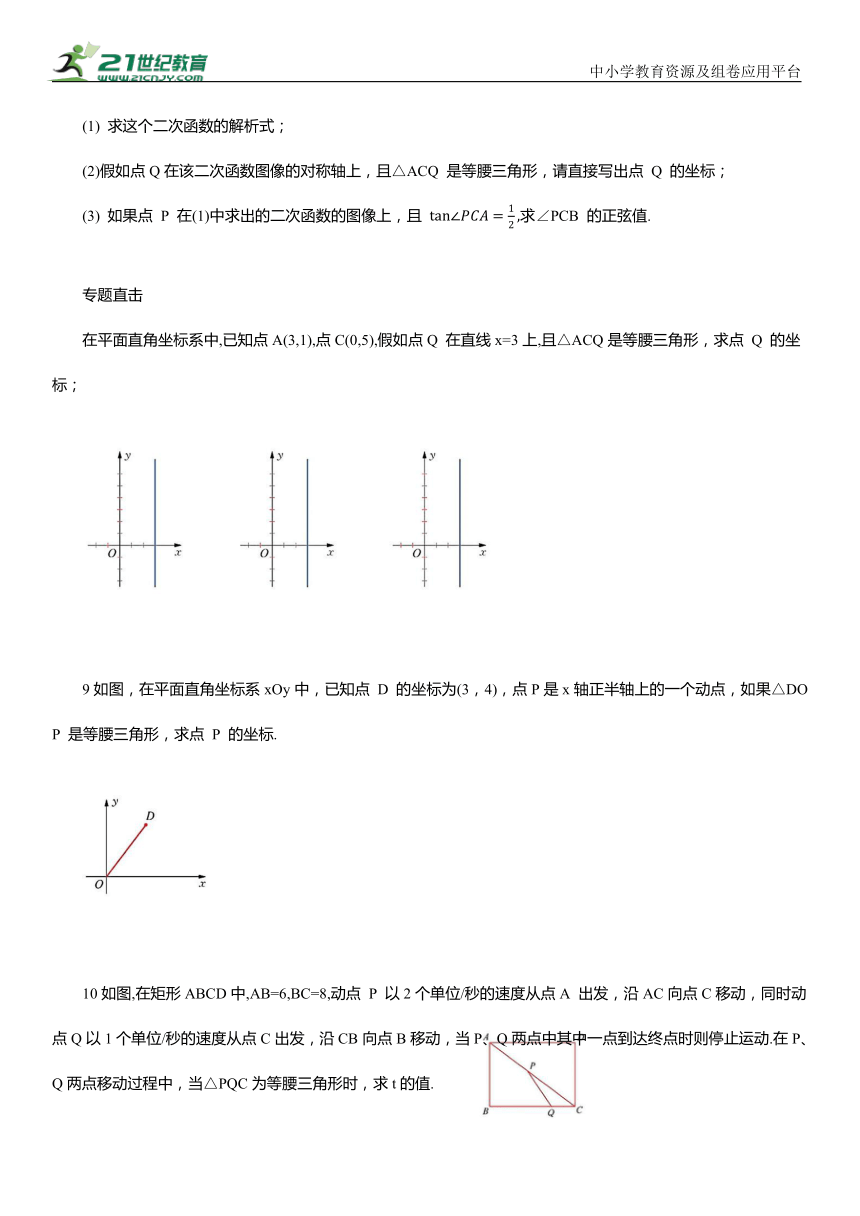
在平面直角坐标系中,已知点A(3,1),点C(0,5),假如点Q 在直线x=3上,且△ACQ是等腰三角形,求点 Q 的坐标;
9如图,在平面直角坐标系xOy中,已知点 D 的坐标为(3,4),点P是x轴正半轴上的一个动点,如果△DOP 是等腰三角形,求点 P 的坐标.
10如图,在矩形ABCD中,AB=6,BC=8,动点 P 以2个单位/秒的速度从点A 出发,沿AC向点C移动,同时动点Q以1个单位/秒的速度从点C出发,沿CB向点B移动,当P、Q两点中其中一点到达终点时则停止运动.在P、Q两点移动过程中,当△PQC为等腰三角形时,求t的值.
1满分解答
(1)设抛物线的交点式为y=a(x+1)(x--3),代入点A(--2,5),得5=5a.
解得a=1.所以 .对称轴是直线x=1.
(2)如图2,因为点C'落在抛物线的对称轴上,所以(
因为翻折前后的对应线段相等,所以(
所以△C'BC 是等边三角形.
因为对称轴BD 平分∠C'BC,所以∠DBC=30°.
设抛物线的对称轴与x 轴交于点 H.
在等边三角形C'BC中,BH=2,所以( 所以C'(1, 2
在Rt△BDH 中,∠DBH=30°, BH =2,所以 所以
(3) 等边三角形 BCC'与等边三角形QCP 有一个公共顶点C.分两种情况讨论.
①如图3,当点 P 在x轴上方时,∠BCQ绕着点C顺时针旋转60°与△C'CP 重合.
所以PC'=QB,PC=QC.
当点 Q 落在对称轴上时,QB=QC.
等量代换,得 所以点 P 在线段CC'的垂直平分线上.
又因为直线BD 垂直平分线段CC',所以直线BP 就是直线BD.
由B(-1,0), D(1,2 ),得直线 BP 的解析式为
② 如图4,当点 P 在x轴下方时,△BCP 绕着点C顺时针旋转60°与△C'CQ重合.
所以∠PBC=∠QC'C.
当点 Q落在对称轴上时, 等量代换,得
设直线BP 与y轴交于点E,那么
由 得直线 BP 的解析式为
考点伸展
第(3)题两种情况的解法不同,是因为“手拉手”模型中,旋转全等的三角形不同.根本原因是两个等边三角形 PCQ 不同,图3中线段CP 绕点C 逆时针旋转60°得到等边三角形 PCQ,图4中线段CP 绕点C 顺时针旋转60°得到等边三角形 PCQ.
2.满分解答
(1)点A(2,0)关于对称轴x=-1的对称点为B(-4,0),设y=a(x-2)(x+4).
代入点C(0,-2),得--2=-8a.
解得 所以抛物线的解析式为
(2)由B(-4,0)、C(0, - 2),可得直线 BC 的解析式为
设
所以
由 得 解得x=-5,或x=0(舍去).
所以
所以
(3) 如图2,
分两种情况讨论以BD 为腰的等腰三角形BDM.作MH⊥x 轴于H.
①如图3,BM=BD=1.在 Rt△MBH中,
所以 此时
②如图4,DB=DM=1.设MH=m,BH=2m,那么在Rt△MDH中,由勾股定理,得 解得
所以 此时
考点伸展
第(3)题如果没有以BD 为腰的限定,还存在第③种情况:如图5,当MD=MB 时,点M在DB 的垂直平分线上.所以
此时
讨论等腰三角形BDM,用代数法方便一些.已知B(-4,0)、D(-5,0),设
所以
然后分三种情况 列方程求解.
3.满分解答
(1) 在 Rt△ACD中,CD=6,AD=8,所以.
等腰三角形 PCD 存在三种情况:
①如图2,当PC=PD时,点 P 在CD的垂直平分线上,此时P是AC的中点,AP=5.
②如图3,当CP=CD=6时,AP=10-6=4.
③如图4,当DP=DC时,由 得 所以
(2)如图5,过点P作PM⊥AD 于M,交BC于N,那么△PNE∽△DMP.
所以 所以
如图6,由∠PDF=∠ADC=90°,得∠CDF=∠ADP.
所以△CDF∽△ADP.所以 所以
考点伸展
在本题情景下,点P 从点A 向点C 运动的过程中,点F 运动的路径长是多少
由于△DCF∽△DAP,所以∠DCF=∠DAP 为定值,所以点 F 的路径为一条线段.
如图7,当点 E 与点C重合时,点F 运动停止.
此时 ,即点 F 运动的路径长是
4.满分解答
(1) 抛物线L 的解析式是
(2)如图3,由y= kx--k+4=k(x--1)+4,可知不论k为何值,当x=1时,y=4.
所以直线 MN 过定点Q(1,4),点Q 在抛物线的对称轴上.
由 得B(1,2).所以QB=2.
联立 和y= kx-k+4,消去y,整理,得x +(k-2)x+3-k=0.
解得 所以.
过点 M、N分别向对称轴作垂线,垂足分别为M′、N′.
所以
解方程 得k=-3,或k=3(不符合题意,舍去).
(3) 第一段,说理、计算,求m 的值.
首先,如图4,∠OPF =∠CPD 总是存在的,且 所以
因此∠OPF 与∠CPD 互余只能存在一种情况.
已知OC=1+m.设PO=n,那么CP=1+m-n.
如图5,由 得 整理,得
解 得 或 (舍去).
所以当 时,恰有2个点 P 符合△PCD 与△POF 相似.
此时
第二段,分两种情况求点 P 的坐标.
①如图4,当∠OPF=∠CPD时, 所以
②如图5,当∠OPF 与∠CPD 互余时, 解得 所以P(0, ).
考点伸展
第(3)题的几何意义就是以DF 为直径的⊙G与y轴相切于点P 时,△PCD与 相似,并且符合条件的点 P 恰有2个.如果⊙G与y轴相交,那么有3个点 P 符合△PCD与 相似.如果⊙G与y轴相离,那么只有1个点 P 符合△PCD 与△POF 相似.
5满分解答
(1)如图2,设AD=CD=x.
在Rt△DOC 中,DO=2-x,CO=1,由勾股定理,得
解得 所以 所以
(2)如图3,若E是弧AB的中点,那么EA=EB.
又因为EA=EC,所以EB=EC.
联结OE,那么OE=OB.
又因为∠B 是两个等腰三角形的公共底角,所以△OBE∽△EBC.
所以 于是得到
(3)如图4,因为△DCE≌△DAE,我们讨论以AD 为腰的等腰三角形DAE:
①如图5,当AD=AE时,由于AD=CD,AE=CE,所以四边形ADCE 是菱形此时EC⊥OB.
因为 所以4x-
整理,得 解得
②如图6,当DA=DE时,点 D 在AE 的垂直平分线上.
而弦AE 的垂直平分线一定经过原点O,所以点 D 与点O 重合.
此时点C与点B 重合,CD=2.
考点伸展
等腰三角形 DAE 的第3种情况EA =ED 怎么讨论呢
如图7,讨论ED=DC比较方便.此时点 E 在CD 的垂直平分线上.
由垂径定理,可知半径OE 垂直平分弦AB,所以DC ∥AB.
所以△DOC 是等腰直角三角形.此时
解方程 得
6满分解答
(1) 将B(1,0)、C(0, 3)分别代入. 得解得 所以.y=-x -2x+3=-(x+3)(x-1)=-(x+1) +4.
所以A(-3,0),顶点 D(-1,4).
(2) 如图2,设抛物线的对称轴与x轴交于点E.
在 Rt△DAE 中,
如图3,作BF⊥AC于F.
在Rt△AOC中,OA=OC=3,所以∠A=45°, AC=3
在等腰直角三角形ABF中,AB=4,所以.
在Rt△BCF中,( 所以
由tan∠DAB=∠ACB=2,得∠DAB=∠ACB.
(3)如图4,作AD 的垂直平分线,与抛物线交于点Q,垂足为H,那么△ADQ是以AD 为底的等腰三角形.
由A(-3,0)、D(-1,4),得中点 H(-3,2).设(
过点 H 作y轴的平行线,过D、Q分别作y轴的垂线,构造 Rt△DNH ∽Rt△HMQ.
由 得 整理,得
解得
所以 或
考点伸展
第(3)题也可以联立方程组求点 Q 的坐标.
设AD的垂直平分线与x轴交于点G,垂足为H,那么.
由于 的三边比为 由此可计算出AG 的长,得到G(2, 0).
由 H(-3,2)、G(2,0)得到直线 HG 的解析式为
然后联立直线 HG 与抛物线的解析式,解方程组得到两个点 Q 的坐标.
7满分解答
(1) 由 得A(-3,0),B(4,0),C(0,-4).
(2) 点Q 的坐标为 或(1,-3).
(3)第一段,说理.
如图2,由 PE ∥AC,得∠1=∠2.
又因为∠2与∠3互余,所以∠3与∠1互余.
因为∠1为定值,所以∠3为定值.
如图3,由 PM∥y轴,所以∠PQF =∠BCO=45°为定值.
所以△QFP 的形状是确定的.当QP 取得最大值时,QF 也取得最大值.
第二段,用m 表示QP.
由B(4,0)、C(0,-4),得直线BC 的解析式为y=x-4.
所以
所以
第三段,用m 表示QF.如图4,作FH⊥QP 于H.
由 所以
在△QFP中,设FH=3a, PH=4a,那么QH=3a.所以(
由QP=7a,得 所以
所以当m=2时,QP 和QF 都取得最大值.
考点伸展
第(2)题的思路是这样的:已知A(-3,0),C(0, - 4),所以AC=5.
因为点Q在直线BC:y=x-4上,设Q(m,m-4).
分三种情况讨论等腰三角形ACQ:
①如图5,如果AQ=AC=5,|由 得 解得m=1,或m=0(Q与C重合,舍去).
②如图6,如果CQ=CA=5,那么 解得 舍去负值).
③如图7,如果QA=QC,由 得 解得m=12.5(此时点Q在CB 的延长线上,舍去).
8满分解答
(1)由B(6,5)、C(0,5),可知抛物线的对称轴是直线x=3.
由 A(3,1),可知点 A 是抛物线的顶点.
设二次函数的解析式为 代入点B(6,5),得9a+1=5.
解得 所以
(2)点Q的坐标为(3,6),(3,—4), (3,9)或(3,
(3)如图2,绕着点A 将线段AC的中点旋转90°得到点D,那么射线CD 与抛物线的交点就是要求的点 P.
当点 D 在CA 左侧时,射线CD 与抛物线没有交点.
如图3,当点 D 在CA 右侧时,作DE⊥x 轴于E,那么∠DCE 就是∠PCB.
过点A 作x轴的平行线交y轴于M,过点 D 作DN⊥AM于N.
由△CMA∽△AND,得
所以
在 Rt△CDE 中,CE=MA+AN=3+2=5,ED=CM-ND=4- = 所以tan∠DCE= 所以 即
考点伸展
第(2)题分三种情况讨论等腰三角形ACQ:
①如图4,当AQ=AC=5时,以A为圆心、以AC为半径的圆与对称轴有两个交点,所以点Q的坐标为(3,6)或(3,-4).
②如图5,当CQ=CA 时,点C在AQ 的垂直平分线上,此时点Q 的坐标为(3,9).
③如图6,当QA=QC时,点Q在AC 的垂直平分线上,此时
所以 此时点 Q 的坐标为
9.满分解答
因为 D(3, 4),所以
①如图1,当PD=PO时,作 PE⊥OD 于E.
在 Rt△OPE中, 所以
此时点 P 的坐标为
②如图2,当OP=OD=5时,点 P 的坐标为(5,0).
③如图3,当DO=DP 时,点D 在OP 的垂直平分线上,此时点 P 的坐标为(6,0).
10满分解答
在Rt△ABC中, 因此 在△PQC中,CQ=t,CP=10--2t.
①如图1,当CP=CQ时,t=10-2t,解得 (秒).
②如图2,当QP=QC时,过点Q作QM⊥AC 于M,则 在Rt△QMC 中, 解得 (秒).
③如图3,当PQ=PC时,过点 P 作PN⊥BC于N,则
在 Rt△PNC 中, 解得 (秒).
综上所述,当t 为 秒、 秒、 秒时,△PQC 为等腰三角形.
等腰三角形的存在性问题
1. 如图1,抛物线 经过点A(-2,5),与x轴相交于点B(-1,0),C(3,0)两点.
(1) 求抛物线的函数表达式;
(2) 点D 在抛物线的对称轴上,且位于x轴的上方,将△BCD 沿直线BD 翻折得到△BC'D,若点C'恰好落在抛物线的对称轴上,求点 C'和点D 的坐标;
(3) 设P 是抛物线上位于对称轴右侧的一点,点Q 在抛物线的对称轴上,当△CPQ 为等边三角形时,求直线 BP 的函数表达式.
2. 如图1,抛物线与 x 轴交于A、B两点,与y 轴交于点C(0,—2),点A 的坐标是(2,0), P 为抛物线上的一个动点,过点 P 作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.
(1)求抛物线的函数表达式;
(2) 若点 P 在第二象限内,且 求△PBE 的面积;
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD 为腰的等腰三角形 若存在,求出点 M 的坐标;若不存在,说明理由.
3如图1,矩形ABCD中,AB=6,BC=8,P、E分别是线段AC、BC上 A的点,四边形 PEFD 是矩形,连结CF.
(1) 若△PCD 为等腰三角形,求 AP 的长;
(2)若 求CF 的长.
4. 抛物线L: 经过点A(0,1),与它的对称轴直线x=1交于点 B.
(1) 直接写出抛物线L 的解析式;
(2)如图1,过定点的直线y= kx-k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k 的值;
(3)如图2,将抛物线L 向上平移m(m>0)个单位长度得到抛物线L ,抛物线L 与y轴交于点C,过点C作y轴的垂线交抛物线L 于另一点D. F为抛物线L 的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF 相似,并且符合条件的点P恰有2个,求m的值及相应点P 的坐标.
思路点拨
1. 第(2)题探究定点的方法,可以把解析式的中含k的项提取k,就可以看到当x=1时,不论k 为何值,y的值都为4.
2. 探究得到的定点Q 也在对称轴上,这样求不规则△BMN 的面积就可以割补了.
3. 第(3)题恰有2个点 P 的意义,就是∠DPF 等于90°只存在一种情况.
5如图1,在半径为2的扇形AOB中,∠AOB =90°,点C 在半径OB 上,AC 的垂直平分线交OA 于点D,交弧AB 于点E,联结BE、CD.
(1) 若C 是半径OB 中点,求∠OCD 的正弦值;
(2) 若E 是弧AB 的中点,求证:
(3) 联结CE,当△DCE 是以CD 为腰的等腰三角形时,求CD 的长.
6如图1,已知在平面直角坐标系中,抛物线. 与x轴交于点 A 和点B(1,0),与y轴相交于点C(0,3).
(1) 求抛物线的解析式和顶点 D 的坐标;
(2)求证:∠DAB=∠ACB;
(3) 点Q 在抛物线上,且△ADQ 是以AD 为底的等腰三角形,求点Q的坐标.
7如图1,抛物线 与x轴交于A、B两点(点A 在点B 的左侧),与y轴交于点C,连接AC、BC.点P 是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为M, PM交BC于点Q,过点P作PE∥AC交x轴于点E,交 BC 于点F.
(1)求A、B、C三点的坐标;
(2) 试探究在点 P 运动的过程中,是否存在这样的点 Q,使得以A、C、Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;
(3) 请用含 m 的代数式表示线段QF 的长,并求出m 为何值时QF 有最大值.
8如图1,在平面直角坐标系中,已知点A 的坐标为(3,1),点B 的坐标为(6,5),点C 的坐标为(0,5),某二次函数的图像经过A、B、C三点.
(1) 求这个二次函数的解析式;
(2)假如点Q在该二次函数图像的对称轴上,且△ACQ 是等腰三角形,请直接写出点 Q 的坐标;
(3) 如果点 P 在(1)中求出的二次函数的图像上,且 求∠PCB 的正弦值.
专题直击
在平面直角坐标系中,已知点A(3,1),点C(0,5),假如点Q 在直线x=3上,且△ACQ是等腰三角形,求点 Q 的坐标;
9如图,在平面直角坐标系xOy中,已知点 D 的坐标为(3,4),点P是x轴正半轴上的一个动点,如果△DOP 是等腰三角形,求点 P 的坐标.
10如图,在矩形ABCD中,AB=6,BC=8,动点 P 以2个单位/秒的速度从点A 出发,沿AC向点C移动,同时动点Q以1个单位/秒的速度从点C出发,沿CB向点B移动,当P、Q两点中其中一点到达终点时则停止运动.在P、Q两点移动过程中,当△PQC为等腰三角形时,求t的值.
1满分解答
(1)设抛物线的交点式为y=a(x+1)(x--3),代入点A(--2,5),得5=5a.
解得a=1.所以 .对称轴是直线x=1.
(2)如图2,因为点C'落在抛物线的对称轴上,所以(
因为翻折前后的对应线段相等,所以(
所以△C'BC 是等边三角形.
因为对称轴BD 平分∠C'BC,所以∠DBC=30°.
设抛物线的对称轴与x 轴交于点 H.
在等边三角形C'BC中,BH=2,所以( 所以C'(1, 2
在Rt△BDH 中,∠DBH=30°, BH =2,所以 所以
(3) 等边三角形 BCC'与等边三角形QCP 有一个公共顶点C.分两种情况讨论.
①如图3,当点 P 在x轴上方时,∠BCQ绕着点C顺时针旋转60°与△C'CP 重合.
所以PC'=QB,PC=QC.
当点 Q 落在对称轴上时,QB=QC.
等量代换,得 所以点 P 在线段CC'的垂直平分线上.
又因为直线BD 垂直平分线段CC',所以直线BP 就是直线BD.
由B(-1,0), D(1,2 ),得直线 BP 的解析式为
② 如图4,当点 P 在x轴下方时,△BCP 绕着点C顺时针旋转60°与△C'CQ重合.
所以∠PBC=∠QC'C.
当点 Q落在对称轴上时, 等量代换,得
设直线BP 与y轴交于点E,那么
由 得直线 BP 的解析式为
考点伸展
第(3)题两种情况的解法不同,是因为“手拉手”模型中,旋转全等的三角形不同.根本原因是两个等边三角形 PCQ 不同,图3中线段CP 绕点C 逆时针旋转60°得到等边三角形 PCQ,图4中线段CP 绕点C 顺时针旋转60°得到等边三角形 PCQ.
2.满分解答
(1)点A(2,0)关于对称轴x=-1的对称点为B(-4,0),设y=a(x-2)(x+4).
代入点C(0,-2),得--2=-8a.
解得 所以抛物线的解析式为
(2)由B(-4,0)、C(0, - 2),可得直线 BC 的解析式为
设
所以
由 得 解得x=-5,或x=0(舍去).
所以
所以
(3) 如图2,
分两种情况讨论以BD 为腰的等腰三角形BDM.作MH⊥x 轴于H.
①如图3,BM=BD=1.在 Rt△MBH中,
所以 此时
②如图4,DB=DM=1.设MH=m,BH=2m,那么在Rt△MDH中,由勾股定理,得 解得
所以 此时
考点伸展
第(3)题如果没有以BD 为腰的限定,还存在第③种情况:如图5,当MD=MB 时,点M在DB 的垂直平分线上.所以
此时
讨论等腰三角形BDM,用代数法方便一些.已知B(-4,0)、D(-5,0),设
所以
然后分三种情况 列方程求解.
3.满分解答
(1) 在 Rt△ACD中,CD=6,AD=8,所以.
等腰三角形 PCD 存在三种情况:
①如图2,当PC=PD时,点 P 在CD的垂直平分线上,此时P是AC的中点,AP=5.
②如图3,当CP=CD=6时,AP=10-6=4.
③如图4,当DP=DC时,由 得 所以
(2)如图5,过点P作PM⊥AD 于M,交BC于N,那么△PNE∽△DMP.
所以 所以
如图6,由∠PDF=∠ADC=90°,得∠CDF=∠ADP.
所以△CDF∽△ADP.所以 所以
考点伸展
在本题情景下,点P 从点A 向点C 运动的过程中,点F 运动的路径长是多少
由于△DCF∽△DAP,所以∠DCF=∠DAP 为定值,所以点 F 的路径为一条线段.
如图7,当点 E 与点C重合时,点F 运动停止.
此时 ,即点 F 运动的路径长是
4.满分解答
(1) 抛物线L 的解析式是
(2)如图3,由y= kx--k+4=k(x--1)+4,可知不论k为何值,当x=1时,y=4.
所以直线 MN 过定点Q(1,4),点Q 在抛物线的对称轴上.
由 得B(1,2).所以QB=2.
联立 和y= kx-k+4,消去y,整理,得x +(k-2)x+3-k=0.
解得 所以.
过点 M、N分别向对称轴作垂线,垂足分别为M′、N′.
所以
解方程 得k=-3,或k=3(不符合题意,舍去).
(3) 第一段,说理、计算,求m 的值.
首先,如图4,∠OPF =∠CPD 总是存在的,且 所以
因此∠OPF 与∠CPD 互余只能存在一种情况.
已知OC=1+m.设PO=n,那么CP=1+m-n.
如图5,由 得 整理,得
解 得 或 (舍去).
所以当 时,恰有2个点 P 符合△PCD 与△POF 相似.
此时
第二段,分两种情况求点 P 的坐标.
①如图4,当∠OPF=∠CPD时, 所以
②如图5,当∠OPF 与∠CPD 互余时, 解得 所以P(0, ).
考点伸展
第(3)题的几何意义就是以DF 为直径的⊙G与y轴相切于点P 时,△PCD与 相似,并且符合条件的点 P 恰有2个.如果⊙G与y轴相交,那么有3个点 P 符合△PCD与 相似.如果⊙G与y轴相离,那么只有1个点 P 符合△PCD 与△POF 相似.
5满分解答
(1)如图2,设AD=CD=x.
在Rt△DOC 中,DO=2-x,CO=1,由勾股定理,得
解得 所以 所以
(2)如图3,若E是弧AB的中点,那么EA=EB.
又因为EA=EC,所以EB=EC.
联结OE,那么OE=OB.
又因为∠B 是两个等腰三角形的公共底角,所以△OBE∽△EBC.
所以 于是得到
(3)如图4,因为△DCE≌△DAE,我们讨论以AD 为腰的等腰三角形DAE:
①如图5,当AD=AE时,由于AD=CD,AE=CE,所以四边形ADCE 是菱形此时EC⊥OB.
因为 所以4x-
整理,得 解得
②如图6,当DA=DE时,点 D 在AE 的垂直平分线上.
而弦AE 的垂直平分线一定经过原点O,所以点 D 与点O 重合.
此时点C与点B 重合,CD=2.
考点伸展
等腰三角形 DAE 的第3种情况EA =ED 怎么讨论呢
如图7,讨论ED=DC比较方便.此时点 E 在CD 的垂直平分线上.
由垂径定理,可知半径OE 垂直平分弦AB,所以DC ∥AB.
所以△DOC 是等腰直角三角形.此时
解方程 得
6满分解答
(1) 将B(1,0)、C(0, 3)分别代入. 得解得 所以.y=-x -2x+3=-(x+3)(x-1)=-(x+1) +4.
所以A(-3,0),顶点 D(-1,4).
(2) 如图2,设抛物线的对称轴与x轴交于点E.
在 Rt△DAE 中,
如图3,作BF⊥AC于F.
在Rt△AOC中,OA=OC=3,所以∠A=45°, AC=3
在等腰直角三角形ABF中,AB=4,所以.
在Rt△BCF中,( 所以
由tan∠DAB=∠ACB=2,得∠DAB=∠ACB.
(3)如图4,作AD 的垂直平分线,与抛物线交于点Q,垂足为H,那么△ADQ是以AD 为底的等腰三角形.
由A(-3,0)、D(-1,4),得中点 H(-3,2).设(
过点 H 作y轴的平行线,过D、Q分别作y轴的垂线,构造 Rt△DNH ∽Rt△HMQ.
由 得 整理,得
解得
所以 或
考点伸展
第(3)题也可以联立方程组求点 Q 的坐标.
设AD的垂直平分线与x轴交于点G,垂足为H,那么.
由于 的三边比为 由此可计算出AG 的长,得到G(2, 0).
由 H(-3,2)、G(2,0)得到直线 HG 的解析式为
然后联立直线 HG 与抛物线的解析式,解方程组得到两个点 Q 的坐标.
7满分解答
(1) 由 得A(-3,0),B(4,0),C(0,-4).
(2) 点Q 的坐标为 或(1,-3).
(3)第一段,说理.
如图2,由 PE ∥AC,得∠1=∠2.
又因为∠2与∠3互余,所以∠3与∠1互余.
因为∠1为定值,所以∠3为定值.
如图3,由 PM∥y轴,所以∠PQF =∠BCO=45°为定值.
所以△QFP 的形状是确定的.当QP 取得最大值时,QF 也取得最大值.
第二段,用m 表示QP.
由B(4,0)、C(0,-4),得直线BC 的解析式为y=x-4.
所以
所以
第三段,用m 表示QF.如图4,作FH⊥QP 于H.
由 所以
在△QFP中,设FH=3a, PH=4a,那么QH=3a.所以(
由QP=7a,得 所以
所以当m=2时,QP 和QF 都取得最大值.
考点伸展
第(2)题的思路是这样的:已知A(-3,0),C(0, - 4),所以AC=5.
因为点Q在直线BC:y=x-4上,设Q(m,m-4).
分三种情况讨论等腰三角形ACQ:
①如图5,如果AQ=AC=5,|由 得 解得m=1,或m=0(Q与C重合,舍去).
②如图6,如果CQ=CA=5,那么 解得 舍去负值).
③如图7,如果QA=QC,由 得 解得m=12.5(此时点Q在CB 的延长线上,舍去).
8满分解答
(1)由B(6,5)、C(0,5),可知抛物线的对称轴是直线x=3.
由 A(3,1),可知点 A 是抛物线的顶点.
设二次函数的解析式为 代入点B(6,5),得9a+1=5.
解得 所以
(2)点Q的坐标为(3,6),(3,—4), (3,9)或(3,
(3)如图2,绕着点A 将线段AC的中点旋转90°得到点D,那么射线CD 与抛物线的交点就是要求的点 P.
当点 D 在CA 左侧时,射线CD 与抛物线没有交点.
如图3,当点 D 在CA 右侧时,作DE⊥x 轴于E,那么∠DCE 就是∠PCB.
过点A 作x轴的平行线交y轴于M,过点 D 作DN⊥AM于N.
由△CMA∽△AND,得
所以
在 Rt△CDE 中,CE=MA+AN=3+2=5,ED=CM-ND=4- = 所以tan∠DCE= 所以 即
考点伸展
第(2)题分三种情况讨论等腰三角形ACQ:
①如图4,当AQ=AC=5时,以A为圆心、以AC为半径的圆与对称轴有两个交点,所以点Q的坐标为(3,6)或(3,-4).
②如图5,当CQ=CA 时,点C在AQ 的垂直平分线上,此时点Q 的坐标为(3,9).
③如图6,当QA=QC时,点Q在AC 的垂直平分线上,此时
所以 此时点 Q 的坐标为
9.满分解答
因为 D(3, 4),所以
①如图1,当PD=PO时,作 PE⊥OD 于E.
在 Rt△OPE中, 所以
此时点 P 的坐标为
②如图2,当OP=OD=5时,点 P 的坐标为(5,0).
③如图3,当DO=DP 时,点D 在OP 的垂直平分线上,此时点 P 的坐标为(6,0).
10满分解答
在Rt△ABC中, 因此 在△PQC中,CQ=t,CP=10--2t.
①如图1,当CP=CQ时,t=10-2t,解得 (秒).
②如图2,当QP=QC时,过点Q作QM⊥AC 于M,则 在Rt△QMC 中, 解得 (秒).
③如图3,当PQ=PC时,过点 P 作PN⊥BC于N,则
在 Rt△PNC 中, 解得 (秒).
综上所述,当t 为 秒、 秒、 秒时,△PQC 为等腰三角形.
同课章节目录
