枣庄市阴平中学2024-2025学年七年级上期末数学模拟试卷(含解析)
文档属性
| 名称 | 枣庄市阴平中学2024-2025学年七年级上期末数学模拟试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 739.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年枣庄市阴平中学七年级上数学期末模拟试卷
时间120分钟 满分120分
一.选择题(每小题3分,共36分)
1.﹣2024的相反数是( )
A.﹣2024 B.2024 C. D.﹣
2.一个正方体的棱长之和是6dm,这个正方体的体积是( )
A.1dm3 B.0.25dm3 C.0.125dm3 D.12.5cm3
3.学习了“点动成线,线动成面,面动成体”,下列说法不正确的是( )
A.将长方形沿一边旋转一周一定会得到一个圆柱
B.将半圆形沿直径旋转一周一定会得到一个球体
C.将直角三角形沿一边旋转一周一定会得到一个圆锥
D.将正方形沿一边旋转一周一定会得到一个圆柱
4.如图,一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示,则C对面的字母是( )
A.A B.B C.D D.F
5.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A.3.84×104 B.3.84×105 C.3.84×106 D.38.4×105
6.已知|a|=5,|b|=4,且a+b<0,则a﹣b的值是( )
A.9或1 B.﹣1或﹣9 C.9或﹣1 D.﹣9或1
7.下列各组单项式中,不是同类项的是( )
A.4a2n与﹣7an2 B.与
C.2abx2与 D.4a2y与
8.已知M=4x2﹣3x﹣2,N=6x2﹣3x+6,则M与N的大小关系是( )
A.M<N B.M>N C.M=N D.以上都有可能
9.如图,点D是线段AC上一点,点C是线段AB的中点,则下列结论:①AD+BD=AB;②BD﹣CD=AC;③AB=2AC;④AD=AC.其中正确的个数为( )
题9 题12 题13
A.4个 B.3个 C.2个 D.1个
10.下列说法错误的是( )
A.9时30分时钟表的时针和分针的夹角是105°
B.若AB=BC,则点B是线段AC的中点
C.直线AB和直线BA表示同一条直线
D.过七边形一个顶点的所有对角线将七边形分成5个三角形
11.下列等式变形,不一定正确的是( )
A.由2x+5=﹣1,得2x=﹣1﹣5 B.若a﹣3=b﹣3,则a=b
C.如果,那么x=﹣8 D.若a=b,则
12.正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1.若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,转1次后,点B所对应的数为2;则翻转2024次后,数轴上数2024所对应的点是( )
A.点C B.点D C.点A D.点B
二.填空题(每小题3分,共18分)
13.如图,将三角形沿虚线剪去一个角,剩下的四边形周长小于原三角形的周长,理由是 .
14.由百色站至南宁站的某趟动车,运行途中停靠的车站依次是:百色站—田阳站—田东站—平果站—隆安站—南宁站,那么铁路运营公司要为这条路线制作的往返车票有 种.
15.小红在解关于x的方程:﹣3x+1=3a﹣2时,误将方程中的“﹣3”看成了“3”,求得方程的解为x=1,则原方程的解为 .
16.若(x+1)2+|y﹣2024|=0,则xy= .
17.某公交车上原有22人,经过3个站点时上、下车情况如下(上车记为正,下车记为负):(+3,﹣7),(+6,﹣4),(+2,﹣1),则车上还有 人.
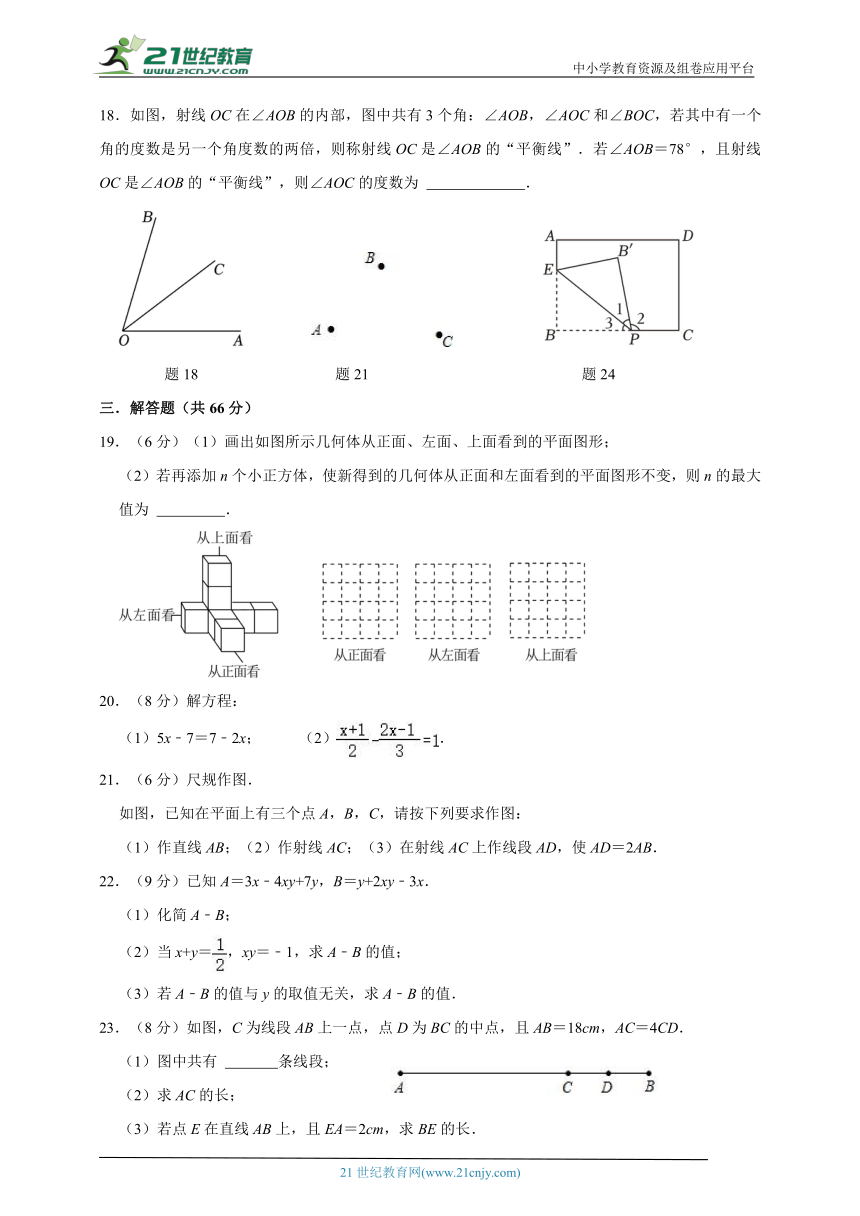
18.如图,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“平衡线”.若∠AOB=78°,且射线OC是∠AOB的“平衡线”,则∠AOC的度数为 .
题18 题21 题24
三.解答题(共66分)
19.(6分)(1)画出如图所示几何体从正面、左面、上面看到的平面图形;
(2)若再添加n个小正方体,使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为 .
20.(8分)解方程:
(1)5x﹣7=7﹣2x; (2).
21.(6分)尺规作图.
如图,已知在平面上有三个点A,B,C,请按下列要求作图:
(1)作直线AB;(2)作射线AC;(3)在射线AC上作线段AD,使AD=2AB.
22.(9分)已知A=3x﹣4xy+7y,B=y+2xy﹣3x.
(1)化简A﹣B;
(2)当x+y=,xy=﹣1,求A﹣B的值;
(3)若A﹣B的值与y的取值无关,求A﹣B的值.
23.(8分)如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
24.(8分)若∠α和∠β均为大于0°小于180°的角,且|∠α﹣∠β|=60°,则称∠α和∠β互为“伙伴角”.根据这个约定,解答下列问题:
(1)若∠α和∠β互为“伙伴角”,当∠α=130°时,求∠β的度数;
(2)如图,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点B',若∠1与∠2互为“伙伴角”,求∠3的度数.
25.(9分)目前,某市市区居民用管道天然气继续执行阶梯价格制度.各阶梯价格水平如下:
一户居民一年用气量(单位:立方米) 电价(单位:元/立方米)
第1档 不超过300立方米的部分 2.8
第2档 300立方米以上至600立方米(含)部分 3.2
第3档 600立方米以上的部分 4
(1)小明家2023年用气100立方米,小明家2023年应缴费 元.
(2)若某户2023年用气量为x立方米,当x>600时,则应缴费 元(用含x的代数式表示).
(3)按照此方案结算,某户2023年实际缴纳燃气费1640元,求该户2023年实际用气量为多少立方米?
26.(12分)对有理数a,b定义了一种新的运算,叫“乘加法”,记作“a b”.并按照此运算写出了一些式子:2 3=5,(﹣2) 3=﹣5,2 (﹣3)=﹣5,(﹣2) (﹣3)=5,(﹣2) (﹣2)=4,2 (﹣2)=﹣4,2 0=2,(﹣2) 0=2,
(1)根据以上式子特点将“乘加法”法则补充完整:
同号得 ,异号得 ,并把绝对值 ;一个数与0相“乘加”等于 ;
(2)根据法则计算:(﹣4) 2= ; (﹣3)= ;
(3)若括号的作用与它在有理数运算中的作用相同,请计算:
①[(﹣11) 0] (﹣4); ②[6 (﹣1)] [(﹣1) ].
阴平中学2024-2025学年七年级上数学期末模拟考试试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B C C A B B A. A B B D
题号 12
答案 B
一.选择题
1.﹣2024的相反数是( )
A.﹣2024 B.2024 C. D.﹣
【解答】解:﹣2024的相反数是2024,
故选:B.
2.一个正方体的棱长之和是6dm,这个正方体的体积是( )
A.1dm3 B.0.25dm3 C.0.125dm3 D.12.5cm3
【解答】解:∵正方体的棱长之和是6dm,
∴每一条棱长为0.5dm,
∴体积为0.5×0.5×0.5=0.125(dm3).
故选:C.
3.学习了“点动成线,线动成面,面动成体”,下列说法不正确的是( )
A.将长方形沿一边旋转一周一定会得到一个圆柱
B.将半圆形沿直径旋转一周一定会得到一个球体
C.将直角三角形沿一边旋转一周一定会得到一个圆锥
D.将正方形沿一边旋转一周一定会得到一个圆柱
【解答】解:A.将长方形沿一边旋转一周一定会得到一个圆柱,故不符合题意;
B.将半圆形沿直径旋转一周一定会得到一个球体,故不符合题意;
C.将直角三角形沿直角边旋转一周一定会得到一个圆锥,故符合题意;
D.将正方形沿一边旋转一周一定会得到一个圆柱,故不符合题意.
故选:C.
4.如图,一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示,则C对面的字母是( )
A.A B.B C.D D.F
【解答】解:由图可知,A相邻的四个面上的字母是B、D、E、F,
所以,字母C的对面是字母A.
故选:A.
5.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A.3.84×104 B.3.84×105 C.3.84×106 D.38.4×105
【解答】解:384000=3.84×105.
故选:B.
6.已知|a|=5,|b|=4,且a+b<0,则a﹣b的值是( )
A.9或1 B.﹣1或﹣9 C.9或﹣1 D.﹣9或1
【解答】解:∵|a|=5,|b|=4,
∴a=±5,b=±4,
∵a+b<0,
∴a=﹣5,b=4或a=﹣5,b=﹣4,
∴a﹣b=﹣5﹣4=﹣9或a﹣b=﹣5﹣(﹣4)=﹣1,
∴a﹣b的值为﹣9或﹣1.
故选:B.
7.下列各组单项式中,不是同类项的是( )
A.4a2n与﹣7an2 B.与
C.2abx2与 D.4a2y与
【解答】解:A、相同字母的指数不相同,不是同类项;
B、符合同类项的定义,是同类项;
C、符合同类项的定义,是同类项;
D、符合同类项的定义,是同类项;
故选:A.
8.已知M=4x2﹣3x﹣2,N=6x2﹣3x+6,则M与N的大小关系是( )
A.M<N B.M>N
C.M=N D.以上都有可能
【解答】解:∵M﹣N=(4x2﹣3x﹣2)﹣(6x2﹣3x+6)
=4x2﹣3x﹣2﹣6x2+3x﹣6
=﹣2x2﹣8<0,
所以M<N.
故选:A.
9.如图,点D是线段AC上一点,点C是线段AB的中点,则下列结论:①AD+BD=AB;②BD﹣CD=AC;③AB=2AC;④AD=AC.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
【解答】解:由图形可知,AD+BD=AB,故①正确;
∵点C是线段AB的中点,
∴AC=BC=AC,
∴BD﹣CD=BC=AC,故②正确;
∵点C是线段AB的中点,
∴AB=2AC,故③正确;
∵D是不是线段AC的中点,
∴AD≠AC,故④错误..
故选:B.
10.下列说法错误的是( )
A.9时30分时钟表的时针和分针的夹角是105°
B.若AB=BC,则点B是线段AC的中点
C.直线AB和直线BA表示同一条直线
D.过七边形一个顶点的所有对角线将七边形分成5个三角形
【解答】解:9时30分时,钟表的时针指向9和10中间,分针指向6,因此时针和分针的夹角=,故A选项说法正确;
当A,B,C不在同一条直线上时,若AB=BC,则点B不是线段AC的中点,故选项B说法错误;
两点确定一条直线,可知直线AB和直线BA表示同一条直线,故选项C说法正确;
从n边形的一个顶点引出的所有对角线把这个n边形分成了(n﹣2)个三角形,因此过七边形一个顶点的所有对角线将七边形分成5个三角形,故选项D说法正确;
故选:B.
11.下列等式变形,不一定正确的是( )
A.由2x+5=﹣1,得2x=﹣1﹣5
B.若a﹣3=b﹣3,则a=b
C.如果,那么x=﹣8
D.若a=b,则
【解答】解:A、由2x+5=﹣1,得2x=﹣1﹣5,故选项正确,不符合题意;
B、若a﹣3=b﹣3,则a=b,故选项正确,不符合题意;
C、如果,那么x=﹣8,故选项正确,不符合题意;
D、若a=b,则(c≠0),故选项错误,符合题意.
故选:D.
12.正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1.若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,转1次后,点B所对应的数为2;则翻转2024次后,数轴上数2024所对应的点是( )
A.点C B.点D C.点A D.点B
【解答】解:正方形连续翻转了4次,第一次翻转A对应1,第二次翻转B对应2,第三次翻转C对应3,第四次D对应4,…,四次一个循环,
∵=506,
∴数轴上数2024所对应的点是D;
故选:B.
二.填空题
13.如图,将三角形沿虚线剪去一个角,剩下的四边形周长小于原三角形的周长,理由是 两点之间,线段最短 .
【解答】解:将三角形沿虚线剪去一个角,剩下的四边形周长小于原三角形的周长,理由是:两点之间,线段最短.
故答案为:两点之间,线段最短.
14.由百色站至南宁站的某趟动车,运行途中停靠的车站依次是:百色站—田阳站—田东站—平果站—隆安站—南宁站,那么铁路运营公司要为这条路线制作的往返车票有 30 种.
【解答】解:如图:
图中线段的条数为5+4+3+2+1=15(条),
15×2=30(种),
即铁路运营公司为这条路线制作的往返车票有30种.
故答案为:30.
15.小红在解关于x的方程:﹣3x+1=3a﹣2时,误将方程中的“﹣3”看成了“3”,求得方程的解为x=1,则原方程的解为 x=﹣1 .
【解答】解:把x=1代入3x+1=3a﹣2,
得3+1=3a﹣2,
解得a=2,
故原方程为﹣3x+1=6﹣2,
﹣3x=3,
解得x=﹣1.
故答案为:x=﹣1.
16.若(x+1)2+|y﹣2024|=0,则xy= 1 .
【解答】解:∵(x+1)2+|y﹣2024|=0,(x+1)2≥0,|y﹣2024|≥0,
∴x+1=0,y﹣2024=0,
∴x=﹣1,y=2024,
则xy=(﹣1)2024=1,
故答案为:1.
17.某公交车上原有22人,经过3个站点时上、下车情况如下(上车记为正,下车记为负):(+3,﹣7),(+6,﹣4),(+2,﹣1),则车上还有 21 人.
【解答】解:22+(﹣7)+3+(﹣4)+6+(﹣1)+2=21(人),
故答案为:21.
18.如图,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“平衡线”.若∠AOB=78°,且射线OC是∠AOB的“平衡线”,则∠AOC的度数为 26°或39°或52° .
【解答】解:由题意,分以下四种情况:
①当∠AOB=2∠AOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,
∴;
②当∠AOB=2∠BOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,
∴,
∴∠AOC=∠AOB﹣∠BOC=39°;
③当∠AOC=2∠BOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,∠AOC+∠BOC=∠AOB,
∴,
解得∠AOC=52°;
④当∠BOC=2∠AOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,∠AOC+∠BOC=∠AOB,
∴∠AOC+2∠AOC=78°,
解得∠AOC=26°;
综上,∠AOC的度数为26°或39°或52°,
故答案为:26°或39°或52°.
三.解答题
19.(1)画出如图所示几何体从正面、左面、上面看到的平面图形;
(2)若再添加n个小正方体,使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为 6 .
【解答】解:(1)三视图如图所示:
(2)使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为6.
故答案为:6.
20.解方程:
(1)5x﹣7=7﹣2x;
(2).
【解答】解:(1)5x﹣7=7﹣2x,
5x+2x=7+7,
7x=14,
x=2;
(2),
3(x+1)﹣2(2x﹣1)=6,
3x+3﹣4x+2=6,
3x﹣4x=6﹣3﹣2,
﹣x=1,
x=﹣1.
21.尺规作图.
如图,已知在平面上有三个点A,B,C,请按下列要求作图:
(1)作直线AB;
(2)作射线AC;
(3)在射线AC上作线段AD,使AD=2AB.
【解答】解:(1)连接AB,并延长AB、BA,得到直线AB;
(2)连接AC,延长AC,得到射线AC;
(3)以A点为圆心,线段AB长为半径作圆,交射线AC于点E,再以E点为圆心,线段AB长为半径作圆,交射线AC于点D,线段AD即是所求.
图形如下:
22.已知A=3x﹣4xy+7y,B=y+2xy﹣3x.
(1)化简A﹣B;
(2)当x+y=,xy=﹣1,求A﹣B的值;
(3)若A﹣B的值与y的取值无关,求A﹣B的值.
【解答】解:(1)∵A=3x﹣4xy+7y,B=y+2xy﹣3x,
∴A﹣B=3x﹣4xy+7y﹣(y+2xy﹣3x)
=3x﹣4xy+7y﹣y﹣2xy+3x
=6x﹣6xy+6y;
(2)∵x+y=,xy=﹣1,
∴A﹣B=6(x+y)﹣6xy
=6×﹣6×(﹣1)
=3+6
=9;
(3)∵A﹣B=6x﹣6xy+6y
=6x﹣6y(x﹣1),
∵A﹣B的值与y的取值无关,
∴x﹣1=0,
∴x=1,
∴A﹣B=6×1﹣0=6.
23.如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 6 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
【解答】解:(1)图中有四个点,线段有=6(条).
故答案为:6;
(2)由点D为BC的中点,得
BC=2CD=2BD,
由线段的和差,得
AB=AC+BC,即4CD+2CD=18cm,
解得CD=3cm,
AC=4CD=4×3=12(cm);
(3)①当点E在线段AB上时,由线段的和差,得
BE=AB﹣AE=18﹣2=16(cm),
②当点E在线段BA的延长线上,由线段的和差,得
BE=AB+AE=18+2=20(cm).
综上所述:BE的长为16cm或20cm.
24.若∠α和∠β均为大于0°小于180°的角,且|∠α﹣∠β|=60°,则称∠α和∠β互为“伙伴角”.根据这个约定,解答下列问题:
(1)若∠α和∠β互为“伙伴角”,当∠α=130°时,求∠β的度数;
(2)如图,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点B',若∠1与∠2互为“伙伴角”,求∠3的度数.
【解答】解:(1)∵∠α和∠β互为“伙伴角”,
∴|∠α﹣∠β|=60°,
∴∠α﹣∠β=60°或∠β﹣∠α=60°,
∴∠β=∠α﹣60°或∠β=∠α+60°,
∵∠α=130°,
∴∠β=70°或∠β=190°,
∵∠α和∠β均为大于0°小于180°的角,
∴∠β=70°;
(2)由折叠的性质得:∠1=∠3,
∵∠1与∠2互为“伙伴角”,
∴|∠1﹣∠2|=60°,
∴∠1﹣∠2=60°或∠2﹣∠1=60°,
∴∠2=∠2﹣60°或∠2=∠1+60°,
∵∠1+∠2+∠3=180°,∠1=∠3,
∴2∠3+∠2=180°,
∴2∠3+∠3﹣60°=180°或2∠3+∠3+60°=180°,
由2∠3+∠3﹣60°=180°,解得:∠3=80°,
由2∠3+∠3+60°=180°,解得:∠3=40°,
综上所述:∠3的度数为80°或40°.
25.目前,某市市区居民用管道天然气继续执行阶梯价格制度.各阶梯价格水平如下:
一户居民一年用气量(单位:立方米) 电价(单位:元/立方米)
第1档 不超过300立方米的部分 2.8
第2档 300立方米以上至600立方米(含)部分 3.2
第3档 600立方米以上的部分 4
(1)小明家2023年用气100立方米,小明家2023年应缴费 280 元.
(2)若某户2023年用气量为x立方米,当x>600时,则应缴费 (4x﹣600) 元(用含x的代数式表示).
(3)按照此方案结算,某户2023年实际缴纳燃气费1640元,求该户2023年实际用气量为多少立方米?
【解答】解:(1)∵小明家2023年用气100立方米,且100<300,
∴小明家2023年应缴费:100×2.8=280(元),
故答案为:280;
(2)∵某户2023年用气量为x立方米,且x>600,
∴应缴费:300×2.8+300×3.2+4(x﹣600)=(4x﹣600)(元),
故答案为:(4x﹣600);
(3)当用天然气300立方米时,费用为:300×2.8=840(元),
当用天然气600立方米时,费用为:300×2.8+300×3.2=1800(元),
∵840<1640<1800,
∴缴纳天然气费1640元,使用量大于300且小于600立方米,
设该户2023年用气量为a立方米,
依题意,得:300×2.8+3.2×(a﹣300)=1640,
解得:a=550,
∴该户2023年实际用气量为550立方米.
26.对有理数a,b定义了一种新的运算,叫“乘加法”,记作“a b”.并按照此运算写出了一些式子:2 3=5,(﹣2) 3=﹣5,2 (﹣3)=﹣5,(﹣2) (﹣3)=5,(﹣2) (﹣2)=4,2 (﹣2)=﹣4,2 0=2,(﹣2) 0=2,
(1)根据以上式子特点将“乘加法”法则补充完整:
同号得 正 ,异号得 负 ,并把绝对值 相加 ;一个数与0相“乘加”等于 这个数的绝对值 ;
(2)根据法则计算:(﹣4) 2= ﹣6 ; (﹣3)= ;
(3)若括号的作用与它在有理数运算中的作用相同,请计算:
①[(﹣11) 0] (﹣4);
②[6 (﹣1)] [(﹣1) ].
【解答】解:(1)同号得正,异号得负,并把绝对值相加;一个数与0相“乘加”等于这个数的绝对值,
故答案为:正,负,相加,这个数的绝对值.
(2)(﹣4) 2=﹣(|﹣4|+|2|)=﹣6;
(﹣3)=||+|﹣3|=3,
故答案为:﹣6;3.
(3)①[(﹣11) 0] (﹣4)
=(11) (﹣4)
=﹣15;
②[6 (﹣1)] [(﹣1) ]
=(﹣7) (﹣1)
=8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年枣庄市阴平中学七年级上数学期末模拟试卷
时间120分钟 满分120分
一.选择题(每小题3分,共36分)
1.﹣2024的相反数是( )
A.﹣2024 B.2024 C. D.﹣
2.一个正方体的棱长之和是6dm,这个正方体的体积是( )
A.1dm3 B.0.25dm3 C.0.125dm3 D.12.5cm3
3.学习了“点动成线,线动成面,面动成体”,下列说法不正确的是( )
A.将长方形沿一边旋转一周一定会得到一个圆柱
B.将半圆形沿直径旋转一周一定会得到一个球体
C.将直角三角形沿一边旋转一周一定会得到一个圆锥
D.将正方形沿一边旋转一周一定会得到一个圆柱
4.如图,一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示,则C对面的字母是( )
A.A B.B C.D D.F
5.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A.3.84×104 B.3.84×105 C.3.84×106 D.38.4×105
6.已知|a|=5,|b|=4,且a+b<0,则a﹣b的值是( )
A.9或1 B.﹣1或﹣9 C.9或﹣1 D.﹣9或1
7.下列各组单项式中,不是同类项的是( )
A.4a2n与﹣7an2 B.与
C.2abx2与 D.4a2y与
8.已知M=4x2﹣3x﹣2,N=6x2﹣3x+6,则M与N的大小关系是( )
A.M<N B.M>N C.M=N D.以上都有可能
9.如图,点D是线段AC上一点,点C是线段AB的中点,则下列结论:①AD+BD=AB;②BD﹣CD=AC;③AB=2AC;④AD=AC.其中正确的个数为( )
题9 题12 题13
A.4个 B.3个 C.2个 D.1个
10.下列说法错误的是( )
A.9时30分时钟表的时针和分针的夹角是105°
B.若AB=BC,则点B是线段AC的中点
C.直线AB和直线BA表示同一条直线
D.过七边形一个顶点的所有对角线将七边形分成5个三角形
11.下列等式变形,不一定正确的是( )
A.由2x+5=﹣1,得2x=﹣1﹣5 B.若a﹣3=b﹣3,则a=b
C.如果,那么x=﹣8 D.若a=b,则
12.正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1.若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,转1次后,点B所对应的数为2;则翻转2024次后,数轴上数2024所对应的点是( )
A.点C B.点D C.点A D.点B
二.填空题(每小题3分,共18分)
13.如图,将三角形沿虚线剪去一个角,剩下的四边形周长小于原三角形的周长,理由是 .
14.由百色站至南宁站的某趟动车,运行途中停靠的车站依次是:百色站—田阳站—田东站—平果站—隆安站—南宁站,那么铁路运营公司要为这条路线制作的往返车票有 种.
15.小红在解关于x的方程:﹣3x+1=3a﹣2时,误将方程中的“﹣3”看成了“3”,求得方程的解为x=1,则原方程的解为 .
16.若(x+1)2+|y﹣2024|=0,则xy= .
17.某公交车上原有22人,经过3个站点时上、下车情况如下(上车记为正,下车记为负):(+3,﹣7),(+6,﹣4),(+2,﹣1),则车上还有 人.
18.如图,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“平衡线”.若∠AOB=78°,且射线OC是∠AOB的“平衡线”,则∠AOC的度数为 .
题18 题21 题24
三.解答题(共66分)
19.(6分)(1)画出如图所示几何体从正面、左面、上面看到的平面图形;
(2)若再添加n个小正方体,使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为 .
20.(8分)解方程:
(1)5x﹣7=7﹣2x; (2).
21.(6分)尺规作图.
如图,已知在平面上有三个点A,B,C,请按下列要求作图:
(1)作直线AB;(2)作射线AC;(3)在射线AC上作线段AD,使AD=2AB.
22.(9分)已知A=3x﹣4xy+7y,B=y+2xy﹣3x.
(1)化简A﹣B;
(2)当x+y=,xy=﹣1,求A﹣B的值;
(3)若A﹣B的值与y的取值无关,求A﹣B的值.
23.(8分)如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
24.(8分)若∠α和∠β均为大于0°小于180°的角,且|∠α﹣∠β|=60°,则称∠α和∠β互为“伙伴角”.根据这个约定,解答下列问题:
(1)若∠α和∠β互为“伙伴角”,当∠α=130°时,求∠β的度数;
(2)如图,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点B',若∠1与∠2互为“伙伴角”,求∠3的度数.
25.(9分)目前,某市市区居民用管道天然气继续执行阶梯价格制度.各阶梯价格水平如下:
一户居民一年用气量(单位:立方米) 电价(单位:元/立方米)
第1档 不超过300立方米的部分 2.8
第2档 300立方米以上至600立方米(含)部分 3.2
第3档 600立方米以上的部分 4
(1)小明家2023年用气100立方米,小明家2023年应缴费 元.
(2)若某户2023年用气量为x立方米,当x>600时,则应缴费 元(用含x的代数式表示).
(3)按照此方案结算,某户2023年实际缴纳燃气费1640元,求该户2023年实际用气量为多少立方米?
26.(12分)对有理数a,b定义了一种新的运算,叫“乘加法”,记作“a b”.并按照此运算写出了一些式子:2 3=5,(﹣2) 3=﹣5,2 (﹣3)=﹣5,(﹣2) (﹣3)=5,(﹣2) (﹣2)=4,2 (﹣2)=﹣4,2 0=2,(﹣2) 0=2,
(1)根据以上式子特点将“乘加法”法则补充完整:
同号得 ,异号得 ,并把绝对值 ;一个数与0相“乘加”等于 ;
(2)根据法则计算:(﹣4) 2= ; (﹣3)= ;
(3)若括号的作用与它在有理数运算中的作用相同,请计算:
①[(﹣11) 0] (﹣4); ②[6 (﹣1)] [(﹣1) ].
阴平中学2024-2025学年七年级上数学期末模拟考试试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B C C A B B A. A B B D
题号 12
答案 B
一.选择题
1.﹣2024的相反数是( )
A.﹣2024 B.2024 C. D.﹣
【解答】解:﹣2024的相反数是2024,
故选:B.
2.一个正方体的棱长之和是6dm,这个正方体的体积是( )
A.1dm3 B.0.25dm3 C.0.125dm3 D.12.5cm3
【解答】解:∵正方体的棱长之和是6dm,
∴每一条棱长为0.5dm,
∴体积为0.5×0.5×0.5=0.125(dm3).
故选:C.
3.学习了“点动成线,线动成面,面动成体”,下列说法不正确的是( )
A.将长方形沿一边旋转一周一定会得到一个圆柱
B.将半圆形沿直径旋转一周一定会得到一个球体
C.将直角三角形沿一边旋转一周一定会得到一个圆锥
D.将正方形沿一边旋转一周一定会得到一个圆柱
【解答】解:A.将长方形沿一边旋转一周一定会得到一个圆柱,故不符合题意;
B.将半圆形沿直径旋转一周一定会得到一个球体,故不符合题意;
C.将直角三角形沿直角边旋转一周一定会得到一个圆锥,故符合题意;
D.将正方形沿一边旋转一周一定会得到一个圆柱,故不符合题意.
故选:C.
4.如图,一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示,则C对面的字母是( )
A.A B.B C.D D.F
【解答】解:由图可知,A相邻的四个面上的字母是B、D、E、F,
所以,字母C的对面是字母A.
故选:A.
5.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A.3.84×104 B.3.84×105 C.3.84×106 D.38.4×105
【解答】解:384000=3.84×105.
故选:B.
6.已知|a|=5,|b|=4,且a+b<0,则a﹣b的值是( )
A.9或1 B.﹣1或﹣9 C.9或﹣1 D.﹣9或1
【解答】解:∵|a|=5,|b|=4,
∴a=±5,b=±4,
∵a+b<0,
∴a=﹣5,b=4或a=﹣5,b=﹣4,
∴a﹣b=﹣5﹣4=﹣9或a﹣b=﹣5﹣(﹣4)=﹣1,
∴a﹣b的值为﹣9或﹣1.
故选:B.
7.下列各组单项式中,不是同类项的是( )
A.4a2n与﹣7an2 B.与
C.2abx2与 D.4a2y与
【解答】解:A、相同字母的指数不相同,不是同类项;
B、符合同类项的定义,是同类项;
C、符合同类项的定义,是同类项;
D、符合同类项的定义,是同类项;
故选:A.
8.已知M=4x2﹣3x﹣2,N=6x2﹣3x+6,则M与N的大小关系是( )
A.M<N B.M>N
C.M=N D.以上都有可能
【解答】解:∵M﹣N=(4x2﹣3x﹣2)﹣(6x2﹣3x+6)
=4x2﹣3x﹣2﹣6x2+3x﹣6
=﹣2x2﹣8<0,
所以M<N.
故选:A.
9.如图,点D是线段AC上一点,点C是线段AB的中点,则下列结论:①AD+BD=AB;②BD﹣CD=AC;③AB=2AC;④AD=AC.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
【解答】解:由图形可知,AD+BD=AB,故①正确;
∵点C是线段AB的中点,
∴AC=BC=AC,
∴BD﹣CD=BC=AC,故②正确;
∵点C是线段AB的中点,
∴AB=2AC,故③正确;
∵D是不是线段AC的中点,
∴AD≠AC,故④错误..
故选:B.
10.下列说法错误的是( )
A.9时30分时钟表的时针和分针的夹角是105°
B.若AB=BC,则点B是线段AC的中点
C.直线AB和直线BA表示同一条直线
D.过七边形一个顶点的所有对角线将七边形分成5个三角形
【解答】解:9时30分时,钟表的时针指向9和10中间,分针指向6,因此时针和分针的夹角=,故A选项说法正确;
当A,B,C不在同一条直线上时,若AB=BC,则点B不是线段AC的中点,故选项B说法错误;
两点确定一条直线,可知直线AB和直线BA表示同一条直线,故选项C说法正确;
从n边形的一个顶点引出的所有对角线把这个n边形分成了(n﹣2)个三角形,因此过七边形一个顶点的所有对角线将七边形分成5个三角形,故选项D说法正确;
故选:B.
11.下列等式变形,不一定正确的是( )
A.由2x+5=﹣1,得2x=﹣1﹣5
B.若a﹣3=b﹣3,则a=b
C.如果,那么x=﹣8
D.若a=b,则
【解答】解:A、由2x+5=﹣1,得2x=﹣1﹣5,故选项正确,不符合题意;
B、若a﹣3=b﹣3,则a=b,故选项正确,不符合题意;
C、如果,那么x=﹣8,故选项正确,不符合题意;
D、若a=b,则(c≠0),故选项错误,符合题意.
故选:D.
12.正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1.若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,转1次后,点B所对应的数为2;则翻转2024次后,数轴上数2024所对应的点是( )
A.点C B.点D C.点A D.点B
【解答】解:正方形连续翻转了4次,第一次翻转A对应1,第二次翻转B对应2,第三次翻转C对应3,第四次D对应4,…,四次一个循环,
∵=506,
∴数轴上数2024所对应的点是D;
故选:B.
二.填空题
13.如图,将三角形沿虚线剪去一个角,剩下的四边形周长小于原三角形的周长,理由是 两点之间,线段最短 .
【解答】解:将三角形沿虚线剪去一个角,剩下的四边形周长小于原三角形的周长,理由是:两点之间,线段最短.
故答案为:两点之间,线段最短.
14.由百色站至南宁站的某趟动车,运行途中停靠的车站依次是:百色站—田阳站—田东站—平果站—隆安站—南宁站,那么铁路运营公司要为这条路线制作的往返车票有 30 种.
【解答】解:如图:
图中线段的条数为5+4+3+2+1=15(条),
15×2=30(种),
即铁路运营公司为这条路线制作的往返车票有30种.
故答案为:30.
15.小红在解关于x的方程:﹣3x+1=3a﹣2时,误将方程中的“﹣3”看成了“3”,求得方程的解为x=1,则原方程的解为 x=﹣1 .
【解答】解:把x=1代入3x+1=3a﹣2,
得3+1=3a﹣2,
解得a=2,
故原方程为﹣3x+1=6﹣2,
﹣3x=3,
解得x=﹣1.
故答案为:x=﹣1.
16.若(x+1)2+|y﹣2024|=0,则xy= 1 .
【解答】解:∵(x+1)2+|y﹣2024|=0,(x+1)2≥0,|y﹣2024|≥0,
∴x+1=0,y﹣2024=0,
∴x=﹣1,y=2024,
则xy=(﹣1)2024=1,
故答案为:1.
17.某公交车上原有22人,经过3个站点时上、下车情况如下(上车记为正,下车记为负):(+3,﹣7),(+6,﹣4),(+2,﹣1),则车上还有 21 人.
【解答】解:22+(﹣7)+3+(﹣4)+6+(﹣1)+2=21(人),
故答案为:21.
18.如图,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“平衡线”.若∠AOB=78°,且射线OC是∠AOB的“平衡线”,则∠AOC的度数为 26°或39°或52° .
【解答】解:由题意,分以下四种情况:
①当∠AOB=2∠AOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,
∴;
②当∠AOB=2∠BOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,
∴,
∴∠AOC=∠AOB﹣∠BOC=39°;
③当∠AOC=2∠BOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,∠AOC+∠BOC=∠AOB,
∴,
解得∠AOC=52°;
④当∠BOC=2∠AOC时,射线OC是∠AOB的“平衡线”,
∵∠AOB=78°,∠AOC+∠BOC=∠AOB,
∴∠AOC+2∠AOC=78°,
解得∠AOC=26°;
综上,∠AOC的度数为26°或39°或52°,
故答案为:26°或39°或52°.
三.解答题
19.(1)画出如图所示几何体从正面、左面、上面看到的平面图形;
(2)若再添加n个小正方体,使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为 6 .
【解答】解:(1)三视图如图所示:
(2)使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为6.
故答案为:6.
20.解方程:
(1)5x﹣7=7﹣2x;
(2).
【解答】解:(1)5x﹣7=7﹣2x,
5x+2x=7+7,
7x=14,
x=2;
(2),
3(x+1)﹣2(2x﹣1)=6,
3x+3﹣4x+2=6,
3x﹣4x=6﹣3﹣2,
﹣x=1,
x=﹣1.
21.尺规作图.
如图,已知在平面上有三个点A,B,C,请按下列要求作图:
(1)作直线AB;
(2)作射线AC;
(3)在射线AC上作线段AD,使AD=2AB.
【解答】解:(1)连接AB,并延长AB、BA,得到直线AB;
(2)连接AC,延长AC,得到射线AC;
(3)以A点为圆心,线段AB长为半径作圆,交射线AC于点E,再以E点为圆心,线段AB长为半径作圆,交射线AC于点D,线段AD即是所求.
图形如下:
22.已知A=3x﹣4xy+7y,B=y+2xy﹣3x.
(1)化简A﹣B;
(2)当x+y=,xy=﹣1,求A﹣B的值;
(3)若A﹣B的值与y的取值无关,求A﹣B的值.
【解答】解:(1)∵A=3x﹣4xy+7y,B=y+2xy﹣3x,
∴A﹣B=3x﹣4xy+7y﹣(y+2xy﹣3x)
=3x﹣4xy+7y﹣y﹣2xy+3x
=6x﹣6xy+6y;
(2)∵x+y=,xy=﹣1,
∴A﹣B=6(x+y)﹣6xy
=6×﹣6×(﹣1)
=3+6
=9;
(3)∵A﹣B=6x﹣6xy+6y
=6x﹣6y(x﹣1),
∵A﹣B的值与y的取值无关,
∴x﹣1=0,
∴x=1,
∴A﹣B=6×1﹣0=6.
23.如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 6 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
【解答】解:(1)图中有四个点,线段有=6(条).
故答案为:6;
(2)由点D为BC的中点,得
BC=2CD=2BD,
由线段的和差,得
AB=AC+BC,即4CD+2CD=18cm,
解得CD=3cm,
AC=4CD=4×3=12(cm);
(3)①当点E在线段AB上时,由线段的和差,得
BE=AB﹣AE=18﹣2=16(cm),
②当点E在线段BA的延长线上,由线段的和差,得
BE=AB+AE=18+2=20(cm).
综上所述:BE的长为16cm或20cm.
24.若∠α和∠β均为大于0°小于180°的角,且|∠α﹣∠β|=60°,则称∠α和∠β互为“伙伴角”.根据这个约定,解答下列问题:
(1)若∠α和∠β互为“伙伴角”,当∠α=130°时,求∠β的度数;
(2)如图,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点B',若∠1与∠2互为“伙伴角”,求∠3的度数.
【解答】解:(1)∵∠α和∠β互为“伙伴角”,
∴|∠α﹣∠β|=60°,
∴∠α﹣∠β=60°或∠β﹣∠α=60°,
∴∠β=∠α﹣60°或∠β=∠α+60°,
∵∠α=130°,
∴∠β=70°或∠β=190°,
∵∠α和∠β均为大于0°小于180°的角,
∴∠β=70°;
(2)由折叠的性质得:∠1=∠3,
∵∠1与∠2互为“伙伴角”,
∴|∠1﹣∠2|=60°,
∴∠1﹣∠2=60°或∠2﹣∠1=60°,
∴∠2=∠2﹣60°或∠2=∠1+60°,
∵∠1+∠2+∠3=180°,∠1=∠3,
∴2∠3+∠2=180°,
∴2∠3+∠3﹣60°=180°或2∠3+∠3+60°=180°,
由2∠3+∠3﹣60°=180°,解得:∠3=80°,
由2∠3+∠3+60°=180°,解得:∠3=40°,
综上所述:∠3的度数为80°或40°.
25.目前,某市市区居民用管道天然气继续执行阶梯价格制度.各阶梯价格水平如下:
一户居民一年用气量(单位:立方米) 电价(单位:元/立方米)
第1档 不超过300立方米的部分 2.8
第2档 300立方米以上至600立方米(含)部分 3.2
第3档 600立方米以上的部分 4
(1)小明家2023年用气100立方米,小明家2023年应缴费 280 元.
(2)若某户2023年用气量为x立方米,当x>600时,则应缴费 (4x﹣600) 元(用含x的代数式表示).
(3)按照此方案结算,某户2023年实际缴纳燃气费1640元,求该户2023年实际用气量为多少立方米?
【解答】解:(1)∵小明家2023年用气100立方米,且100<300,
∴小明家2023年应缴费:100×2.8=280(元),
故答案为:280;
(2)∵某户2023年用气量为x立方米,且x>600,
∴应缴费:300×2.8+300×3.2+4(x﹣600)=(4x﹣600)(元),
故答案为:(4x﹣600);
(3)当用天然气300立方米时,费用为:300×2.8=840(元),
当用天然气600立方米时,费用为:300×2.8+300×3.2=1800(元),
∵840<1640<1800,
∴缴纳天然气费1640元,使用量大于300且小于600立方米,
设该户2023年用气量为a立方米,
依题意,得:300×2.8+3.2×(a﹣300)=1640,
解得:a=550,
∴该户2023年实际用气量为550立方米.
26.对有理数a,b定义了一种新的运算,叫“乘加法”,记作“a b”.并按照此运算写出了一些式子:2 3=5,(﹣2) 3=﹣5,2 (﹣3)=﹣5,(﹣2) (﹣3)=5,(﹣2) (﹣2)=4,2 (﹣2)=﹣4,2 0=2,(﹣2) 0=2,
(1)根据以上式子特点将“乘加法”法则补充完整:
同号得 正 ,异号得 负 ,并把绝对值 相加 ;一个数与0相“乘加”等于 这个数的绝对值 ;
(2)根据法则计算:(﹣4) 2= ﹣6 ; (﹣3)= ;
(3)若括号的作用与它在有理数运算中的作用相同,请计算:
①[(﹣11) 0] (﹣4);
②[6 (﹣1)] [(﹣1) ].
【解答】解:(1)同号得正,异号得负,并把绝对值相加;一个数与0相“乘加”等于这个数的绝对值,
故答案为:正,负,相加,这个数的绝对值.
(2)(﹣4) 2=﹣(|﹣4|+|2|)=﹣6;
(﹣3)=||+|﹣3|=3,
故答案为:﹣6;3.
(3)①[(﹣11) 0] (﹣4)
=(11) (﹣4)
=﹣15;
②[6 (﹣1)] [(﹣1) ]
=(﹣7) (﹣1)
=8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
