2024-2025学年河北省承德市圣泉高级中学高一(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河北省承德市圣泉高级中学高一(上)期中数学试卷(含答案) | 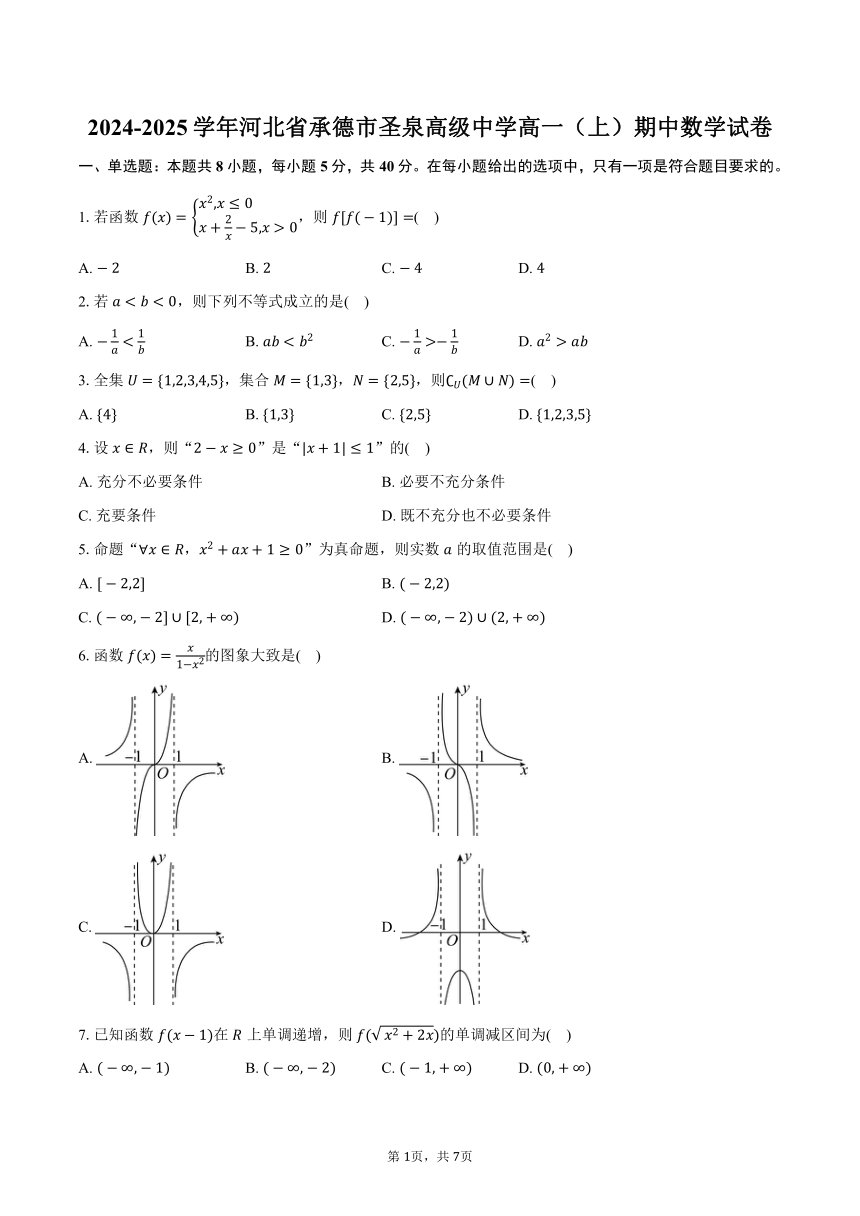 | |
| 格式 | docx | ||
| 文件大小 | 84.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 16:00:06 | ||
图片预览



文档简介
2024-2025学年河北省承德市圣泉高级中学高一(上)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若函数,则( )
A. B. C. D.
2.若,则下列不等式成立的是( )
A. B. C. D.
3.全集,集合,,则( )
A. B. C. D.
4.设,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.命题“,”为真命题,则实数的取值范围是( )
A. B.
C. D.
6.函数的图象大致是( )
A. B.
C. D.
7.已知函数在上单调递增,则的单调减区间为( )
A. B. C. D.
8.已知函数,若对任意,恒成立,则的取值范围为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 函数的图象是一条直线
B. 命题“,都有”的否定是“,使得”
C. 当时,的最小值是
D. ,是的充分不必要条件
10.下列说法正确的有( )
A. 命题“,”的否定是“,”
B. “”是“”的必要条件
C. 命题“,”是假命题
D. “”是“关于的方程有一正一负根”的充要条件
11.已知函数,则下列说法正确的是( )
A. 的对称中心为
B. 的值域为
C. 在区间上单调递增
D. 的值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,,,则的最小值为______.
13.函数在区间上是增函数,则的取值范围是______.
14.设函数,若,则实数的取值范围是______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知:关于的方程有实数根,:.
若命题是真命题,求实数的取值范围;
若是的必要不充分条件,求实数的取值范围.
16.本小题分
已知是定义在上的奇函数.
求的解析式.
证明:在上单调递增.
求不等式的解集.
17.本小题分
已知二次函数,,不等式的解集为或.
求的解析式;
设,不等式的解集为,求实数的取值范围.
18.本小题分
安徽省人民政府办公厅在关于深入开展消费扶贫助力打赢脱贫攻坚战的实施意见中提出要打造区域性特色农产品品牌推动市县或集中连片特殊困难地区制定区域性扶贫产品标识,合力打造区域性特色农产品品牌,提高贫困地区特色农产品辨识度引导各类媒体通过新闻报道、公益广告等多种方式,广泛宣传贫困地区发展特色农产品的经验做法,推介农产品品牌某地区在政策指导下,根据当地气候、土质等条件,推广种植某种市场畅销水果果树经调研发现该果树的单株产量单位:千克与施肥量单位:千克满足函数关系:,且单株果树的肥料成本投入为元,其他成本投入如培育管理、施肥人工费等费用为元已知这种水果的市场售价为元千克,且销路畅通供不应求,记该果树的单株利润为单位:元.
求函数的解析式;
当单株施肥量为多少千克时,该果树的单株利润最大?最大利润是多少?
19.本小题分
已知函数.
当时,求解关于的不等式;
若不等式对于任意的上恒成立,求实数的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解::关于的方程有实数根,:.
因为命题是真命题,则命题是假命题,即关于的方程无实数根,
因此,解得,
所以实数的取值范围是.
由知,命题是真命题,即:,
因为命题是命题的必要不充分条件,则,
因此,解得,
所以实数的取值范围是.
16.解:因为为定义在上的奇函数,
由奇函数性质可得,,
解得,,
又,故,
故,所以,解得,
故,经检验,满足要求;
证明:任取,且,所以且,
则,
所以,故在上单调递增;
因为为定义在上的奇函数,且在上单调递增,
所以在上单调递增,
因为,故,解得,
的解集为.
17.解:二次函数,,不等式的解集为或.
则,则的解集为或,
所以,可得,故;
由的解集为,
所以恒成立,
当时,不恒成立,
所以,可得,
故的范围为
18.解:根据题意知
,
整理得:;
当时,,
由一元二次函数图象可知在时取得最大值,
当时,,
当且仅当,即时等号成立,
所以,
所以的最大值是,
所以当单株施肥量为千克时,该果树的单株利润最大,最大利润是元.
19.解:令,
,,,
当,即时,,原不等式可化为,解得;
当,即时,,解得或;
当,即时,,解得或;
综上:当时,不等式的解集为或.
当时,不等式的解集为或.
,
即对于任意的恒成立,
令,,
当时,,,
不符合题意;
当时,无最小值,不符合题意;
当时,的对称轴为,
当,即时,
,
,
又,不符合题意;
当,即时,
,
,
又,符合题意;
综上,实数的取值范围是.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若函数,则( )
A. B. C. D.
2.若,则下列不等式成立的是( )
A. B. C. D.
3.全集,集合,,则( )
A. B. C. D.
4.设,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.命题“,”为真命题,则实数的取值范围是( )
A. B.
C. D.
6.函数的图象大致是( )
A. B.
C. D.
7.已知函数在上单调递增,则的单调减区间为( )
A. B. C. D.
8.已知函数,若对任意,恒成立,则的取值范围为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 函数的图象是一条直线
B. 命题“,都有”的否定是“,使得”
C. 当时,的最小值是
D. ,是的充分不必要条件
10.下列说法正确的有( )
A. 命题“,”的否定是“,”
B. “”是“”的必要条件
C. 命题“,”是假命题
D. “”是“关于的方程有一正一负根”的充要条件
11.已知函数,则下列说法正确的是( )
A. 的对称中心为
B. 的值域为
C. 在区间上单调递增
D. 的值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,,,则的最小值为______.
13.函数在区间上是增函数,则的取值范围是______.
14.设函数,若,则实数的取值范围是______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知:关于的方程有实数根,:.
若命题是真命题,求实数的取值范围;
若是的必要不充分条件,求实数的取值范围.
16.本小题分
已知是定义在上的奇函数.
求的解析式.
证明:在上单调递增.
求不等式的解集.
17.本小题分
已知二次函数,,不等式的解集为或.
求的解析式;
设,不等式的解集为,求实数的取值范围.
18.本小题分
安徽省人民政府办公厅在关于深入开展消费扶贫助力打赢脱贫攻坚战的实施意见中提出要打造区域性特色农产品品牌推动市县或集中连片特殊困难地区制定区域性扶贫产品标识,合力打造区域性特色农产品品牌,提高贫困地区特色农产品辨识度引导各类媒体通过新闻报道、公益广告等多种方式,广泛宣传贫困地区发展特色农产品的经验做法,推介农产品品牌某地区在政策指导下,根据当地气候、土质等条件,推广种植某种市场畅销水果果树经调研发现该果树的单株产量单位:千克与施肥量单位:千克满足函数关系:,且单株果树的肥料成本投入为元,其他成本投入如培育管理、施肥人工费等费用为元已知这种水果的市场售价为元千克,且销路畅通供不应求,记该果树的单株利润为单位:元.
求函数的解析式;
当单株施肥量为多少千克时,该果树的单株利润最大?最大利润是多少?
19.本小题分
已知函数.
当时,求解关于的不等式;
若不等式对于任意的上恒成立,求实数的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解::关于的方程有实数根,:.
因为命题是真命题,则命题是假命题,即关于的方程无实数根,
因此,解得,
所以实数的取值范围是.
由知,命题是真命题,即:,
因为命题是命题的必要不充分条件,则,
因此,解得,
所以实数的取值范围是.
16.解:因为为定义在上的奇函数,
由奇函数性质可得,,
解得,,
又,故,
故,所以,解得,
故,经检验,满足要求;
证明:任取,且,所以且,
则,
所以,故在上单调递增;
因为为定义在上的奇函数,且在上单调递增,
所以在上单调递增,
因为,故,解得,
的解集为.
17.解:二次函数,,不等式的解集为或.
则,则的解集为或,
所以,可得,故;
由的解集为,
所以恒成立,
当时,不恒成立,
所以,可得,
故的范围为
18.解:根据题意知
,
整理得:;
当时,,
由一元二次函数图象可知在时取得最大值,
当时,,
当且仅当,即时等号成立,
所以,
所以的最大值是,
所以当单株施肥量为千克时,该果树的单株利润最大,最大利润是元.
19.解:令,
,,,
当,即时,,原不等式可化为,解得;
当,即时,,解得或;
当,即时,,解得或;
综上:当时,不等式的解集为或.
当时,不等式的解集为或.
,
即对于任意的恒成立,
令,,
当时,,,
不符合题意;
当时,无最小值,不符合题意;
当时,的对称轴为,
当,即时,
,
,
又,不符合题意;
当,即时,
,
,
又,符合题意;
综上,实数的取值范围是.
第1页,共1页
同课章节目录
