三角形全等的复习课
图片预览



文档简介
课件19张PPT。全等三角形复习平田学校: 叶祥永同一张底片洗出的照片是
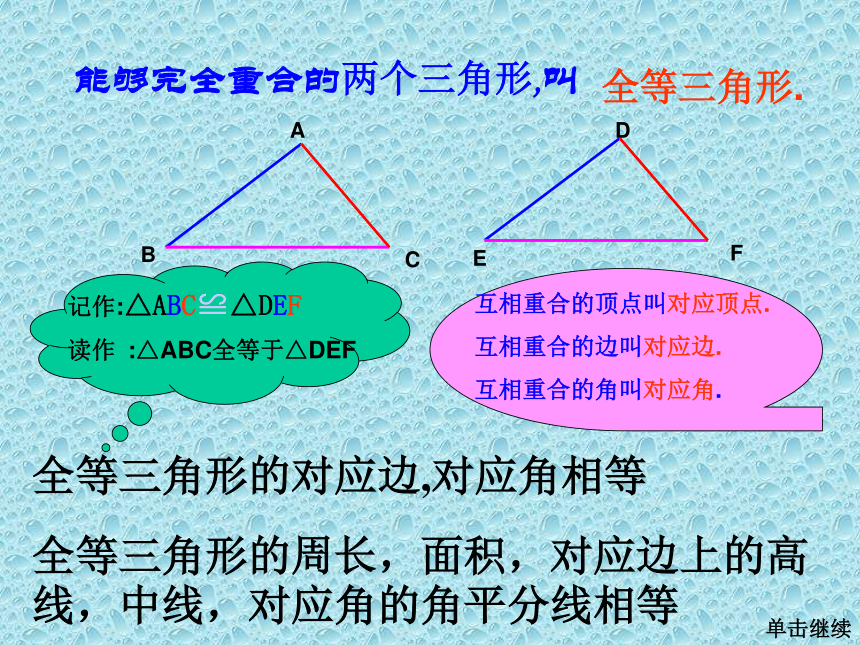
能够完全重合的(1)(2)(3) 能够完全重合的两个图形叫做全等形能够完全重合的两个三角形,叫单击继续全等三角形.全等三角形的对应边,对应角相等
全等三角形的周长,面积,对应边上的高线,中线,对应角的角平分线相等
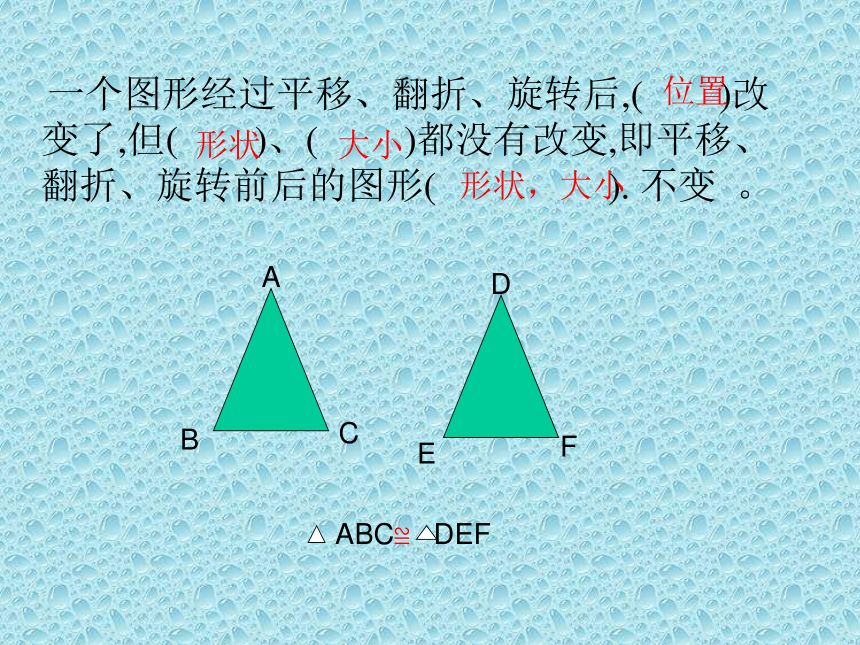
一个图形经过平移、翻折、旋转后,( )改变了,但( )、( )都没有改变,即平移、翻折、旋转前后的图形( ). 不变 。
ABC≌ DEF位置形状 大小形状,大小
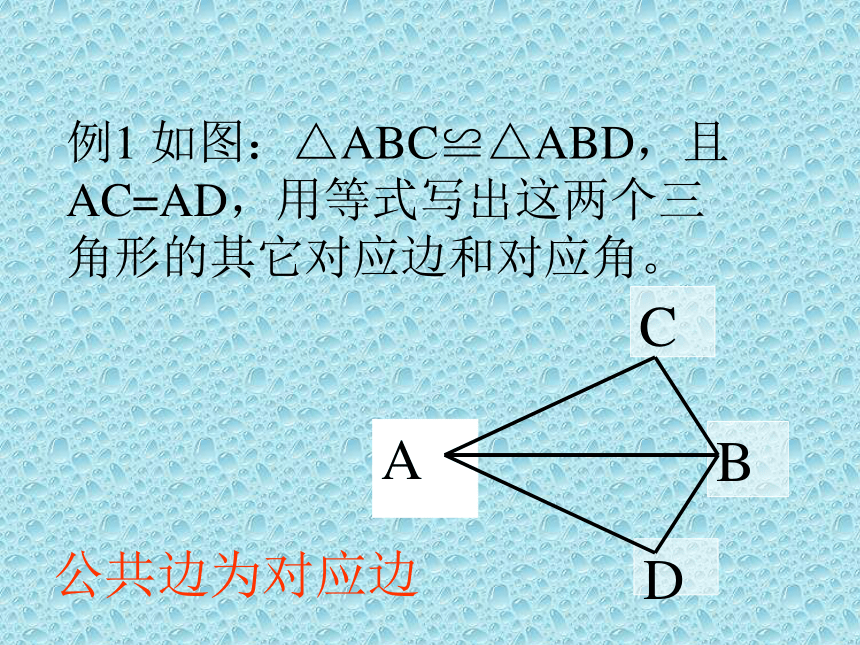
CBA例1 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边找全等三角形对应边和对应角的方法:1、从长短大小两个全等三角形的一对最长边(最大角)是对应边(角);一对最短边(最小角)是对应边(角)2、从对应边与对应角的关系对应角所对的边为对应边;对应边所对的角为对应角;两个对应角所夹的边为对应边;两条对应边所夹的角为对应角。3、从位置公共边为对应边;公共角为对应角;对顶角为对应角 1、 已知如图△ABC≌△DFE,∠A=96o,∠B=25o,DF=10cm。
求 ∠E的度数及AB的长。
BACEDF练习:回忆判定三角形全等有那些方法?SSSSASASA(AAS)直角三角形HL思考题
例2 如图,E,D是⊿ABC中BC边上的两点,AD=AE,
要证明⊿ABE≌⊿ACD,还应该补充一个什么条件。
BDECA解:(1)BE=CD
(2) BD=CE
(3)AB=AC(7)S⊿ABE=S⊿ACD
(8)S⊿ABD=S⊿ACD
(9)⊿ABD≌⊿ACE (4)∠B= ∠ C
(5)∠BAE=∠CAD
(6)∠BAD=∠CAE 练习
2. 测量如图河的宽度,某人在河的对岸找到一参照物树木A, 视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。
15ABODC例3阅读题:已知,如图,BC=BD,∠C=∠D,
求证:AC=AD.
?
答:证法错误。 SAS定理应用错误。有一同学证法如下:
证:连结AB
在⊿ABC和⊿ABD中
BC=BD
∠C=∠D
AB=AB
∴⊿ABC≌⊿ABD ( SAS )
∴AC=AD
你认为这位同学的证法对吗?如果错误,
错在哪里,应怎样证明?
例4:如图A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于点F,DC交BE于G,
(1) 求证:AE=DC (1)证:∵ΔABD和ΔBCE是正三角形∴ΔABE≌ΔDBC∴AB=BD,BC=BE, ∠ABD=∠CBE=600∴∠ABD+∠DBE =∠CBE+∠DBE
即∠ABE=∠DBC∴AE=DC例:如图,A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于点F,DC交BE于点G, (2)求证:BF=BG(2)证:∵ΔABE≌ΔDBC 又∵∠ABD=∠DBE=600
AB=DB∴∠BAE=∠BDC∴ΔAFB≌ΔDGB∴BF=BG例:如图A,B,C三点在同一直线上,分别
以AB,BC为边在AC同侧作等边⊿ABD和
等边⊿BCE,AE交BD于点F,DC交BE
于点G,(3)求∠AHC的度数(3)解:由(1)得,ΔABE≌ΔDBC
∴∠BAE=∠BDC而∠AHC=∠DAH+∠ADH
=∠DAH + ∠ADB +∠BDC∴∠AHC =∠DAH + ∠ADB + ∠BAE∴∠AHC =∠ADB+∠DAB∴∠AHC =1200例:如图,A,B,C三点在同一直线上,分别以AB,
BC为边在AC同侧作等边⊿ABD和等边⊿BCE,
AE交BD于点F,DC交BE于点G,(4)若取AE的中点M, CD的中点N,求证:⊿BMN是等边三角形。∴ BM=BN,∠ABM =∠DBN∴∠MBN =∠MBD+∠DBN
=∠MBD+∠ABM
=∠ABD=600∴ΔBMN是正角形∴CD=AE, M,N分别是AE和DC的中点∴AM=DN(4)证∵ ΔABE≌DBC ∴∠BAM =∠BDN∵ AB=BD∴ ΔABM≌ΔDBN知识点?1. 定义:能够互相重合的两个三角形叫做全等三角形。?2. 基本性质:全等三角形的对应边相等,对应角相等。3. 性质定理:全等三角形对应角的平分线,
对应边上的高线,中线对应相等。4.判定定理:SAS ASA AAS SSS HL 5.应用: 利用全等三角形性质证明两条线段
或两个角相等。小结: 本节利用全等三角形的性质和三角形全等的判定的知识,通过对几何图形的分析和判定,几何图形的移动,旋转变换,探索运动变化过程中不变的量, 进行问题的转化和发展,找出问题的实质来证明和计算,最后解决问题。
请多指教
再 见
能够完全重合的(1)(2)(3) 能够完全重合的两个图形叫做全等形能够完全重合的两个三角形,叫单击继续全等三角形.全等三角形的对应边,对应角相等
全等三角形的周长,面积,对应边上的高线,中线,对应角的角平分线相等
一个图形经过平移、翻折、旋转后,( )改变了,但( )、( )都没有改变,即平移、翻折、旋转前后的图形( ). 不变 。
ABC≌ DEF位置形状 大小形状,大小
CBA例1 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边找全等三角形对应边和对应角的方法:1、从长短大小两个全等三角形的一对最长边(最大角)是对应边(角);一对最短边(最小角)是对应边(角)2、从对应边与对应角的关系对应角所对的边为对应边;对应边所对的角为对应角;两个对应角所夹的边为对应边;两条对应边所夹的角为对应角。3、从位置公共边为对应边;公共角为对应角;对顶角为对应角 1、 已知如图△ABC≌△DFE,∠A=96o,∠B=25o,DF=10cm。
求 ∠E的度数及AB的长。
BACEDF练习:回忆判定三角形全等有那些方法?SSSSASASA(AAS)直角三角形HL思考题
例2 如图,E,D是⊿ABC中BC边上的两点,AD=AE,
要证明⊿ABE≌⊿ACD,还应该补充一个什么条件。
BDECA解:(1)BE=CD
(2) BD=CE
(3)AB=AC(7)S⊿ABE=S⊿ACD
(8)S⊿ABD=S⊿ACD
(9)⊿ABD≌⊿ACE (4)∠B= ∠ C
(5)∠BAE=∠CAD
(6)∠BAD=∠CAE 练习
2. 测量如图河的宽度,某人在河的对岸找到一参照物树木A, 视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。
15ABODC例3阅读题:已知,如图,BC=BD,∠C=∠D,
求证:AC=AD.
?
答:证法错误。 SAS定理应用错误。有一同学证法如下:
证:连结AB
在⊿ABC和⊿ABD中
BC=BD
∠C=∠D
AB=AB
∴⊿ABC≌⊿ABD ( SAS )
∴AC=AD
你认为这位同学的证法对吗?如果错误,
错在哪里,应怎样证明?
例4:如图A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于点F,DC交BE于G,
(1) 求证:AE=DC (1)证:∵ΔABD和ΔBCE是正三角形∴ΔABE≌ΔDBC∴AB=BD,BC=BE, ∠ABD=∠CBE=600∴∠ABD+∠DBE =∠CBE+∠DBE
即∠ABE=∠DBC∴AE=DC例:如图,A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于点F,DC交BE于点G, (2)求证:BF=BG(2)证:∵ΔABE≌ΔDBC 又∵∠ABD=∠DBE=600
AB=DB∴∠BAE=∠BDC∴ΔAFB≌ΔDGB∴BF=BG例:如图A,B,C三点在同一直线上,分别
以AB,BC为边在AC同侧作等边⊿ABD和
等边⊿BCE,AE交BD于点F,DC交BE
于点G,(3)求∠AHC的度数(3)解:由(1)得,ΔABE≌ΔDBC
∴∠BAE=∠BDC而∠AHC=∠DAH+∠ADH
=∠DAH + ∠ADB +∠BDC∴∠AHC =∠DAH + ∠ADB + ∠BAE∴∠AHC =∠ADB+∠DAB∴∠AHC =1200例:如图,A,B,C三点在同一直线上,分别以AB,
BC为边在AC同侧作等边⊿ABD和等边⊿BCE,
AE交BD于点F,DC交BE于点G,(4)若取AE的中点M, CD的中点N,求证:⊿BMN是等边三角形。∴ BM=BN,∠ABM =∠DBN∴∠MBN =∠MBD+∠DBN
=∠MBD+∠ABM
=∠ABD=600∴ΔBMN是正角形∴CD=AE, M,N分别是AE和DC的中点∴AM=DN(4)证∵ ΔABE≌DBC ∴∠BAM =∠BDN∵ AB=BD∴ ΔABM≌ΔDBN知识点?1. 定义:能够互相重合的两个三角形叫做全等三角形。?2. 基本性质:全等三角形的对应边相等,对应角相等。3. 性质定理:全等三角形对应角的平分线,
对应边上的高线,中线对应相等。4.判定定理:SAS ASA AAS SSS HL 5.应用: 利用全等三角形性质证明两条线段
或两个角相等。小结: 本节利用全等三角形的性质和三角形全等的判定的知识,通过对几何图形的分析和判定,几何图形的移动,旋转变换,探索运动变化过程中不变的量, 进行问题的转化和发展,找出问题的实质来证明和计算,最后解决问题。
请多指教
再 见
