第五章 圆 阶段性检测二(第4、5节)(含答案)
文档属性
| 名称 | 第五章 圆 阶段性检测二(第4、5节)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 19:22:58 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
阶段性检测二(第4、5节)
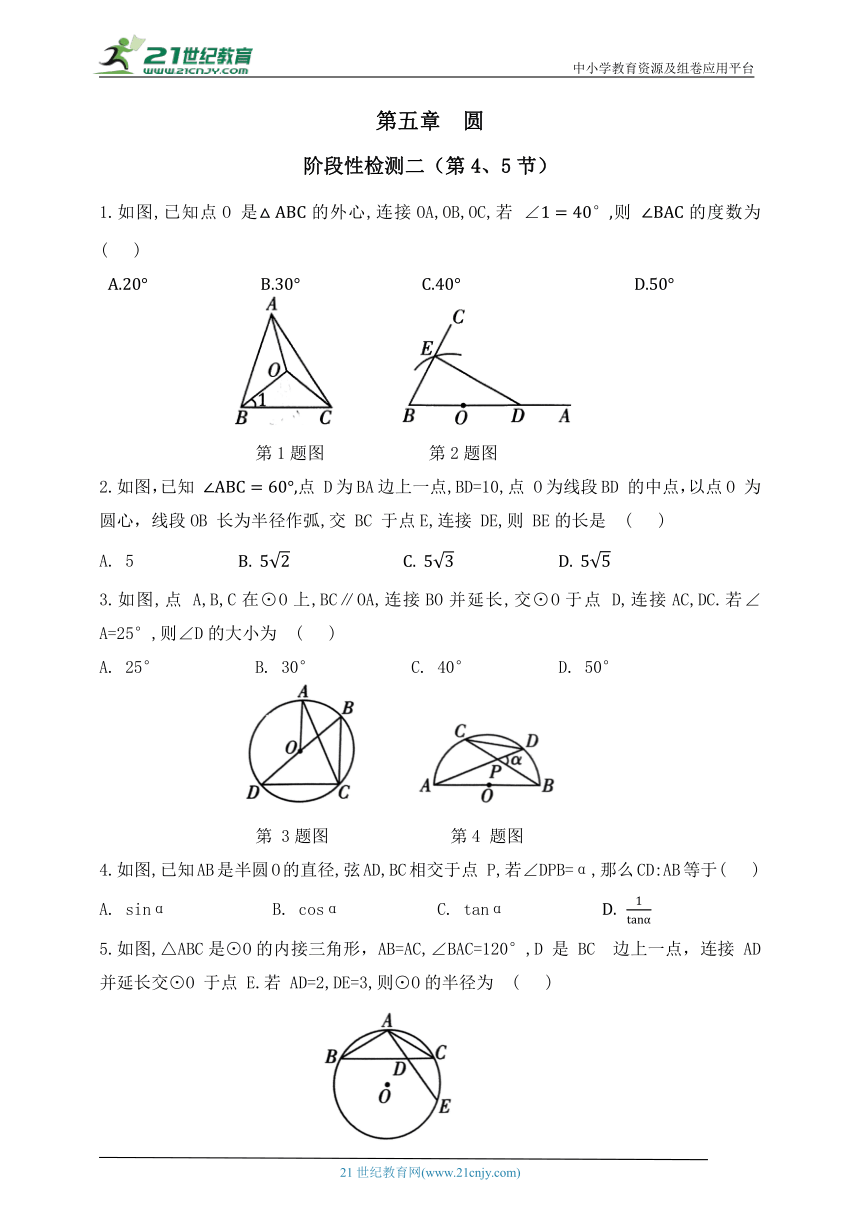
1.如图,已知点O 是的外心,连接OA,OB,OC,若 则 的度数为 ( )
第1题图 第2题图
2.如图,已知 点 D为BA边上一点,BD=10,点 O为线段BD 的中点,以点O 为圆心,线段OB 长为半径作弧,交 BC 于点E,连接 DE,则 BE的长是 ( )
A. 5
3.如图,点 A,B,C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点 D,连接AC,DC.若∠A=25°,则∠D的大小为 ( )
A. 25° B. 30° C. 40° D. 50°
第 3题图 第4 题图
4.如图,已知AB是半圆O的直径,弦AD,BC相交于点 P,若∠DPB=α,那么CD:AB等于( )
A. sinα B. cosα C. tanα
5.如图,△ABC是⊙O的内接三角形,AB=AC,∠BAC=120°,D 是 BC 边上一点,连接 AD 并延长交⊙O 于点 E.若 AD=2,DE=3,则⊙O的半径为 ( )
6.已知A,B,C是⊙O上的三个点,且 60°,那么∠ACB的度数是 ( )
A.30° C.30°或120° D.30°或
7.如图,⊙O是等边的外接圆,点D 是弧AC 上一动点(不与 A,C 重合),下列结论:①∠ADB=∠BDC ②DA=DC ③当DB最长时,DB=2DC ④DA+DC=DB.其中一定正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中 B 点坐标为(4,4),则该圆弧所在圆的圆心坐标为____________.
第8题图 第9题图
9.如图,AB 是圆的直径,∠1,∠2,∠3,∠4 的顶点均在 AB上方的圆弧上,∠1,∠4 的一边分别经过点 A,B,则∠1+∠2+∠3+∠4=___________°.
10.如图,量角器的直径与直角三角板ABC的斜边AB 重合,其中量角器0刻度线的端点 N 与点A 重合,射线CP从CA 处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点 E,第35 秒时,点 E 在量角器上对应的读数是___________度.
11.如图所示,在的正方形网格图中,已知点 A,B,C,D,O均在格点上,其中 A,B,D 又在⊙O上,点 E 是线段 CD与⊙O的交点.则 的正切值为____________.
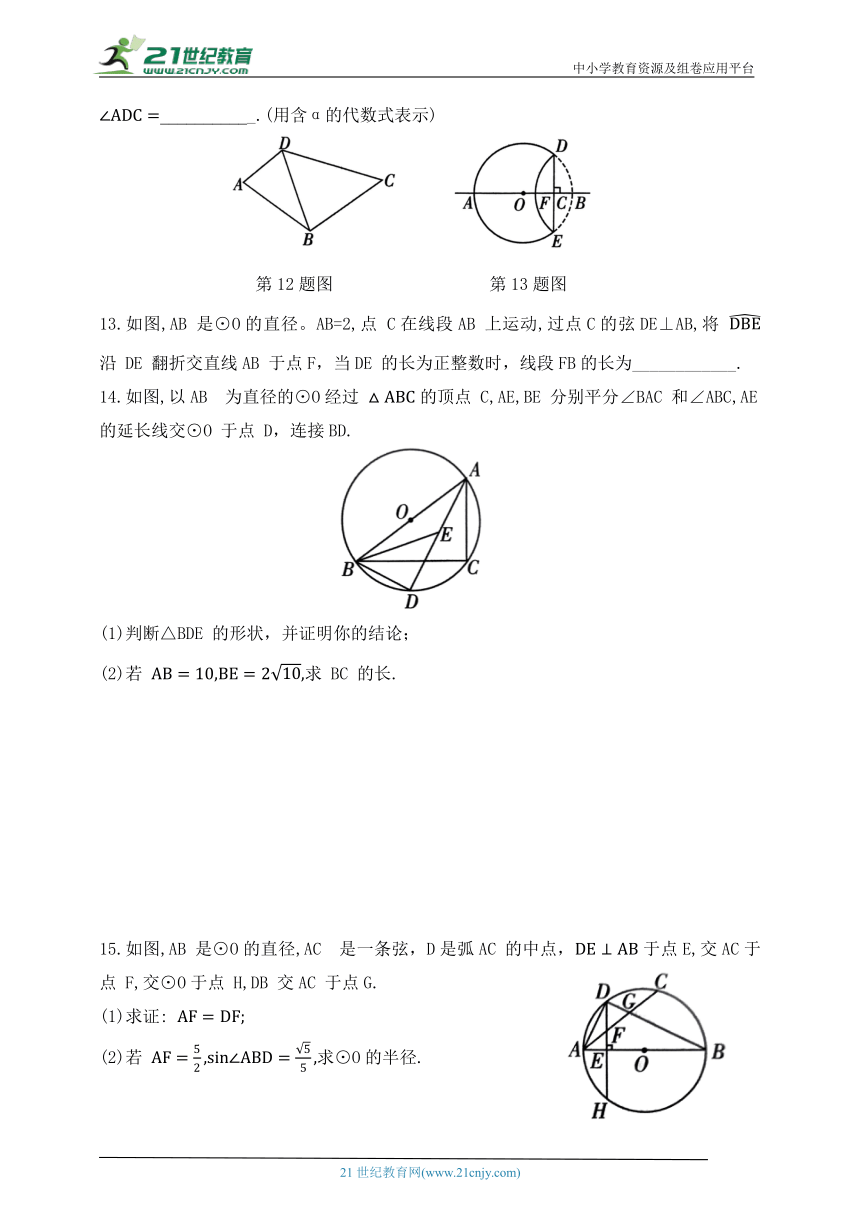
12.如图所示,在四边形ABCD中,设 则 ___________.(用含α的代数式表示)
第12题图 第13题图
13.如图,AB 是⊙O的直径。AB=2,点 C在线段AB 上运动,过点C的弦DE⊥AB,将 沿 DE 翻折交直线AB 于点F,当DE 的长为正整数时,线段FB的长为____________.
14.如图,以AB 为直径的⊙O经过 的顶点 C,AE,BE 分别平分∠BAC 和∠ABC,AE的延长线交⊙O 于点 D,连接BD.
(1)判断△BDE 的形状,并证明你的结论;
(2)若 求 BC 的长.
15.如图,AB 是⊙O的直径,AC 是一条弦,D是弧AC 的中点,于点E,交AC于点 F,交⊙O于点 H,DB 交AC 于点G.
(1)求证:
(2)若 求⊙O的半径.
16.如图,D 是△ABC 的 BC 边上一点,连接AD,作△ABD 的外接圆,将 沿直线AD 折叠,点C的对应点E 落在⊙O上.
(1)求证:
(2)若 2,求 BC的长.
参考答案
1. D 2. A 3. C 4. B 5. A 6. D 7. C
8. (2,0) 9. 90 10. 140 或或2
14.解:(1)△BDE为等腰直角三角形,证明:
∵AE平分∠BAC,BE平分∠ABC,∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,∴∠BED=∠DBE.∴BD=ED.
∵AB为⊙O的直径,∴∠ADB=90°.∴△BDE 是等腰直角三角形;
(2)如图,连接OC,CD,OD,OD交 BC于点 F.
由(1),得∠DBC=∠CAD=∠BAD=∠BCD,∴BD=DC.
∵OB=OC,∴OD 垂直平分BC.
∵△BDE是等腰直角三角形,
∵AB=10,∴OB=OD=5.
设OF=t,则DF=5-t.
在 Rt△BOF 和 Rt△BDF 中,解得t=3.
∴BF=4.∴BC=2BF=8.
15.解:(1)证明:∵D是 AC的中点,
∵AB⊥DH,且AB是⊙O的直径,
∴∠ADH=∠CAD,∴AF=DF;
(2)∵AB是⊙O的直径,∴∠ADB=90°.∴∠DAB+∠B=90°.
∵∠DAE+∠ADE=90°,∴∠ADE=∠B.
设AE=x,则 DE=2x,
∴x=2,
∴⊙O的半径为5.
16.解:(1)由折叠的性质可知,△ADE≌△ADC,∴∠AED=∠ACD,AE=AC.
∵∠ABD=∠AED,∴∠ABD=∠ACD,∴AB=AC,∴AE=AB;
(2)如图,过 A 作 AH⊥BE C于点H,
∵AB=AE,BE=2,∴BH=EH=1.
∵ ∠ABE = ∠AEB =
∴AC=AB=3.
∵∠BAC=90°,AC=AB,∴BC=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
阶段性检测二(第4、5节)
1.如图,已知点O 是的外心,连接OA,OB,OC,若 则 的度数为 ( )
第1题图 第2题图
2.如图,已知 点 D为BA边上一点,BD=10,点 O为线段BD 的中点,以点O 为圆心,线段OB 长为半径作弧,交 BC 于点E,连接 DE,则 BE的长是 ( )
A. 5
3.如图,点 A,B,C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点 D,连接AC,DC.若∠A=25°,则∠D的大小为 ( )
A. 25° B. 30° C. 40° D. 50°
第 3题图 第4 题图
4.如图,已知AB是半圆O的直径,弦AD,BC相交于点 P,若∠DPB=α,那么CD:AB等于( )
A. sinα B. cosα C. tanα
5.如图,△ABC是⊙O的内接三角形,AB=AC,∠BAC=120°,D 是 BC 边上一点,连接 AD 并延长交⊙O 于点 E.若 AD=2,DE=3,则⊙O的半径为 ( )
6.已知A,B,C是⊙O上的三个点,且 60°,那么∠ACB的度数是 ( )
A.30° C.30°或120° D.30°或
7.如图,⊙O是等边的外接圆,点D 是弧AC 上一动点(不与 A,C 重合),下列结论:①∠ADB=∠BDC ②DA=DC ③当DB最长时,DB=2DC ④DA+DC=DB.其中一定正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中 B 点坐标为(4,4),则该圆弧所在圆的圆心坐标为____________.
第8题图 第9题图
9.如图,AB 是圆的直径,∠1,∠2,∠3,∠4 的顶点均在 AB上方的圆弧上,∠1,∠4 的一边分别经过点 A,B,则∠1+∠2+∠3+∠4=___________°.
10.如图,量角器的直径与直角三角板ABC的斜边AB 重合,其中量角器0刻度线的端点 N 与点A 重合,射线CP从CA 处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点 E,第35 秒时,点 E 在量角器上对应的读数是___________度.
11.如图所示,在的正方形网格图中,已知点 A,B,C,D,O均在格点上,其中 A,B,D 又在⊙O上,点 E 是线段 CD与⊙O的交点.则 的正切值为____________.
12.如图所示,在四边形ABCD中,设 则 ___________.(用含α的代数式表示)
第12题图 第13题图
13.如图,AB 是⊙O的直径。AB=2,点 C在线段AB 上运动,过点C的弦DE⊥AB,将 沿 DE 翻折交直线AB 于点F,当DE 的长为正整数时,线段FB的长为____________.
14.如图,以AB 为直径的⊙O经过 的顶点 C,AE,BE 分别平分∠BAC 和∠ABC,AE的延长线交⊙O 于点 D,连接BD.
(1)判断△BDE 的形状,并证明你的结论;
(2)若 求 BC 的长.
15.如图,AB 是⊙O的直径,AC 是一条弦,D是弧AC 的中点,于点E,交AC于点 F,交⊙O于点 H,DB 交AC 于点G.
(1)求证:
(2)若 求⊙O的半径.
16.如图,D 是△ABC 的 BC 边上一点,连接AD,作△ABD 的外接圆,将 沿直线AD 折叠,点C的对应点E 落在⊙O上.
(1)求证:
(2)若 2,求 BC的长.
参考答案
1. D 2. A 3. C 4. B 5. A 6. D 7. C
8. (2,0) 9. 90 10. 140 或或2
14.解:(1)△BDE为等腰直角三角形,证明:
∵AE平分∠BAC,BE平分∠ABC,∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,∴∠BED=∠DBE.∴BD=ED.
∵AB为⊙O的直径,∴∠ADB=90°.∴△BDE 是等腰直角三角形;
(2)如图,连接OC,CD,OD,OD交 BC于点 F.
由(1),得∠DBC=∠CAD=∠BAD=∠BCD,∴BD=DC.
∵OB=OC,∴OD 垂直平分BC.
∵△BDE是等腰直角三角形,
∵AB=10,∴OB=OD=5.
设OF=t,则DF=5-t.
在 Rt△BOF 和 Rt△BDF 中,解得t=3.
∴BF=4.∴BC=2BF=8.
15.解:(1)证明:∵D是 AC的中点,
∵AB⊥DH,且AB是⊙O的直径,
∴∠ADH=∠CAD,∴AF=DF;
(2)∵AB是⊙O的直径,∴∠ADB=90°.∴∠DAB+∠B=90°.
∵∠DAE+∠ADE=90°,∴∠ADE=∠B.
设AE=x,则 DE=2x,
∴x=2,
∴⊙O的半径为5.
16.解:(1)由折叠的性质可知,△ADE≌△ADC,∴∠AED=∠ACD,AE=AC.
∵∠ABD=∠AED,∴∠ABD=∠ACD,∴AB=AC,∴AE=AB;
(2)如图,过 A 作 AH⊥BE C于点H,
∵AB=AE,BE=2,∴BH=EH=1.
∵ ∠ABE = ∠AEB =
∴AC=AB=3.
∵∠BAC=90°,AC=AB,∴BC=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
