第五章 圆 2 圆的对称性(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 圆
2 圆的对称性
1.下列说法中,正确的是 ( )
A.同心圆的周长相等 B.面积相等的圆是等圆
C.相等的圆心角所对的弧相等 D.平分弧的弦一定经过圆心
2.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是 ( )
3.如图,在三个等圆上各自有一条劣弧分别为,,,如果 那么
CD与EF的大小关系是 ( )
D.无法确定
4.如图,在⊙O中,AB是直径, 则的度数为 ( )
第4题图 第5题图
5.如图,AB 是⊙O的直径, 则 的度数是 ( )
6.如图,AB 为⊙O的定直径,过圆上一点 C作弦 的平分线交⊙O于点P,当点 C(不包括A,B 两点)在⊙O上移动时,点P ( )
A.到CD的距离保持不变 B.位置不变 C.等分 D.随C点移动而移动
第6题图 第7题图
7.如图,在扇形OAB 中, 将扇形OAB沿过点 B 的直线折叠,点O恰好落
在 上的点 D 处,折痕交 OA 于点C,则的度数为 ( )
A.40° B.50° C.60° D.70°
8.如图,AB 是⊙O的直径,点 C 是半圆上的一个三等分点,点D 是 的中点,点P 是
直径AB 上一点,若⊙O 的半径为2,则的最小值是__________.
第8题图 第9题图
9.如图,⊙O的直径MN=10,正方形 ABCD的顶点 A,B 在OM 上,顶点 C,D 分别在OP 和 上,且 AB 的长为___________.
10.如图所示,A,B,C,D 是⊙O上的四个点, 与 全等吗 为什么
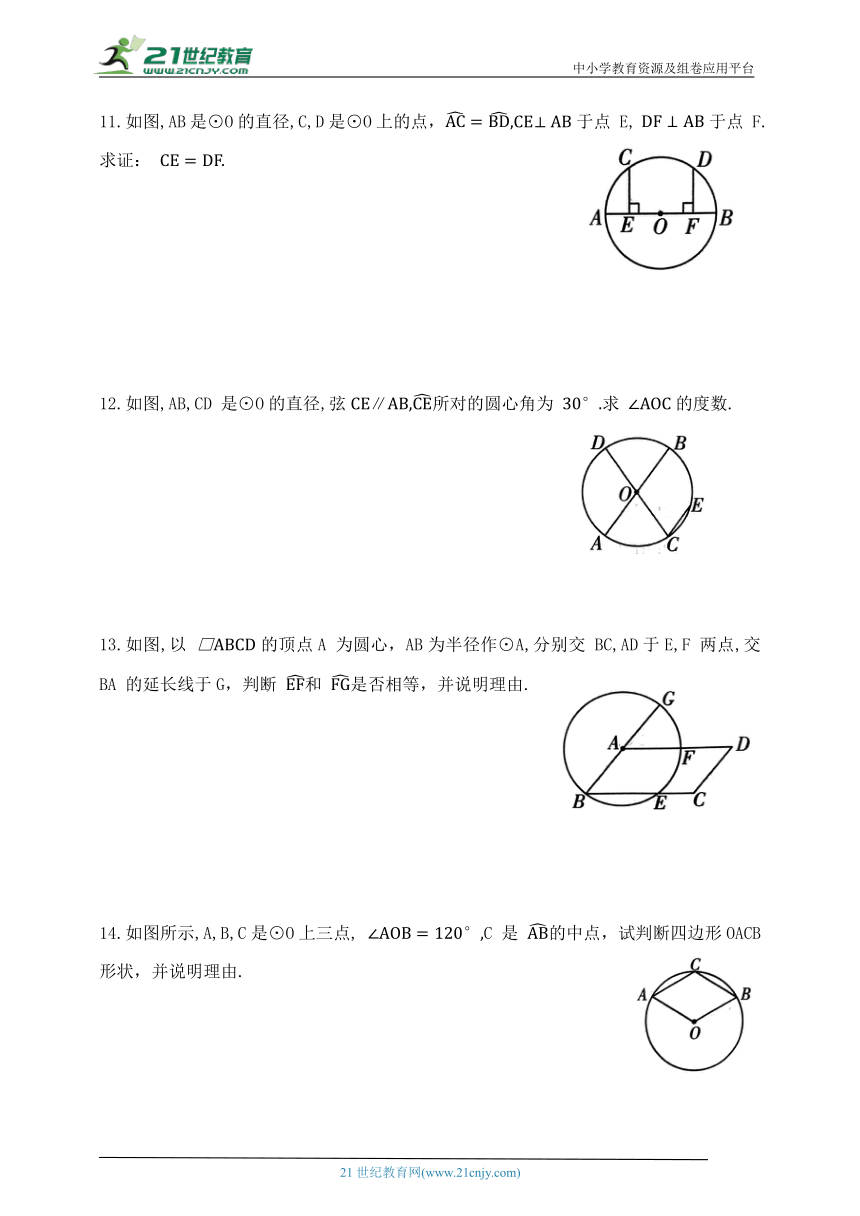
11.如图,AB是⊙O的直径,C,D是⊙O上的点, 于点 E, 于点 F.求证:
12.如图,AB,CD 是⊙O的直径,弦∥所对的圆心角为 求 的度数.
13.如图,以 □的顶点A 为圆心,AB为半径作⊙A,分别交 BC,AD于E,F 两点,交 BA 的延长线于G,判断 和 是否相等,并说明理由.
14.如图所示,A,B,C是⊙O上三点, C 是 的中点,试判断四边形OACB 形状,并说明理由.
15.如图,⊙O的直径AB 与弦DE 交于点 C,且 若 的度数为 求 的度数.
16.在⊙O 中,弦 AB 的长恰等于半径,求弦AB所对圆心角的度数.
17.如图所示, 垂足分别为点 D,E,求证:
18.如图所示,弦AB 所对的劣弧为圆的 圆的半径为4 cm,求 AB 的长度.
19.【抽象能力】如图所示,在 Rt△AOB中,以点 O为圆心,3为半径的⊙O,与OB 交于点C,过点C作CD⊥OB 交AB于点 D,点 P 是边OA 上的点,求 PC+PD的最小值.
参考答案
1. B 2. A 3. B 4. B 5. D
6. B 解析:连接OP,如图,
∵CP平分
∥
又∵弦 ∴OP 平分半圆APB,即点 P 是半圆的中点.
7. B 8.2
10.解:△ABC≌△DCB.理由如下:
即 ∴AC=BD.
又∵BC=BC,∴△ABC≌△DCB(SSS).
11.证明:如图所示,连接OC,OD,
∴∠EOC=∠FOD,
又∵CE⊥AB,DF⊥AB,∴∠OEC=∠OFD=90°,
又∵OC=OD,∴△COE≌△DOF(AAS),∴CE=DF.
12.解:连接OE,如图,
所对的圆心角为30°,∴∠COE=30°,
∵OC=OE,∴∠OCE=∠OEC,∴∠OCE=(180°-30°)÷2=75°,
∵弦CE∥AB,∴∠AOC=∠OCE=75°.
13.解:
理由:连接AE.
∴AB=AE,∴∠B=∠AEB,
∵四边形 ABCD 是平行四边形,∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,∴∠GAF=∠FAE,
14.解:四边形 OACB 是菱形.理由:
如图所示,连接OC.
∵C是 的中点,120°=60°.
∵CO=BO=AO,∴△OBC 是等边三角形,△OCA 是等边三角形,
∴OA=AC=BC=BO,∴四边形OACB 是菱形.
15.解:连接OD,OE,
的度数为40°,∴∠AOD=40°,
∵CD=CO,∴∠D=∠AOD=40°,
∵OD=OE,∴∠E=∠D=40°,∴∠DOE=180°-40°-40°=100°,
∴∠AOE=100°-40°=60°, 的度数是60°.
16.解:由题意知,在△OAB中,OA=OB=AB=r.
∴△OAB 为等边三角形.∴∠AOB=60°.∴弦AB 所对圆心角的度数为 60°.
17.证明:如图所示,连接OC.
∴∠AOC=∠BOC,即OC平分∠AOB,
∵CD⊥OA,CE⊥OB,∴CD=CE.
18.解:由题意,得. AB 的度数为 120°,∴∠AOB=120°.
如图所示,作OC⊥AB,垂足为 C,
∵OA=OB,
在 Rt△AOC中,AC= OA·sin60°= 4×
∴AB的长度为
19.解:延长 CO,交⊙O于点 E,连接 PE,如图所示.
∵OB=6,⊙O以点O为圆心,3为半径,∴OC=BC=OE=3,
∵∠AOB=90°,CD⊥OB,∴∠BCD=∠AOB=90°,AO垂直平分CE,
∴CD∥OA,CP=PE,∴△BCD∽△BOA,
∵OA=4,∴CD=2,∵CP=PE,∴PC+PD=PE+PD,
则要使 PC+PD的值最小,即 PE+PD 的值为最小,
∵PE+PD≥DE,∴当 D,P,E 三点共线时最小,
∴在 Rt△DCE中, ∴PC+PD的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
2 圆的对称性
1.下列说法中,正确的是 ( )
A.同心圆的周长相等 B.面积相等的圆是等圆
C.相等的圆心角所对的弧相等 D.平分弧的弦一定经过圆心
2.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是 ( )
3.如图,在三个等圆上各自有一条劣弧分别为,,,如果 那么
CD与EF的大小关系是 ( )
D.无法确定
4.如图,在⊙O中,AB是直径, 则的度数为 ( )
第4题图 第5题图
5.如图,AB 是⊙O的直径, 则 的度数是 ( )
6.如图,AB 为⊙O的定直径,过圆上一点 C作弦 的平分线交⊙O于点P,当点 C(不包括A,B 两点)在⊙O上移动时,点P ( )
A.到CD的距离保持不变 B.位置不变 C.等分 D.随C点移动而移动
第6题图 第7题图
7.如图,在扇形OAB 中, 将扇形OAB沿过点 B 的直线折叠,点O恰好落
在 上的点 D 处,折痕交 OA 于点C,则的度数为 ( )
A.40° B.50° C.60° D.70°
8.如图,AB 是⊙O的直径,点 C 是半圆上的一个三等分点,点D 是 的中点,点P 是
直径AB 上一点,若⊙O 的半径为2,则的最小值是__________.
第8题图 第9题图
9.如图,⊙O的直径MN=10,正方形 ABCD的顶点 A,B 在OM 上,顶点 C,D 分别在OP 和 上,且 AB 的长为___________.
10.如图所示,A,B,C,D 是⊙O上的四个点, 与 全等吗 为什么
11.如图,AB是⊙O的直径,C,D是⊙O上的点, 于点 E, 于点 F.求证:
12.如图,AB,CD 是⊙O的直径,弦∥所对的圆心角为 求 的度数.
13.如图,以 □的顶点A 为圆心,AB为半径作⊙A,分别交 BC,AD于E,F 两点,交 BA 的延长线于G,判断 和 是否相等,并说明理由.
14.如图所示,A,B,C是⊙O上三点, C 是 的中点,试判断四边形OACB 形状,并说明理由.
15.如图,⊙O的直径AB 与弦DE 交于点 C,且 若 的度数为 求 的度数.
16.在⊙O 中,弦 AB 的长恰等于半径,求弦AB所对圆心角的度数.
17.如图所示, 垂足分别为点 D,E,求证:
18.如图所示,弦AB 所对的劣弧为圆的 圆的半径为4 cm,求 AB 的长度.
19.【抽象能力】如图所示,在 Rt△AOB中,以点 O为圆心,3为半径的⊙O,与OB 交于点C,过点C作CD⊥OB 交AB于点 D,点 P 是边OA 上的点,求 PC+PD的最小值.
参考答案
1. B 2. A 3. B 4. B 5. D
6. B 解析:连接OP,如图,
∵CP平分
∥
又∵弦 ∴OP 平分半圆APB,即点 P 是半圆的中点.
7. B 8.2
10.解:△ABC≌△DCB.理由如下:
即 ∴AC=BD.
又∵BC=BC,∴△ABC≌△DCB(SSS).
11.证明:如图所示,连接OC,OD,
∴∠EOC=∠FOD,
又∵CE⊥AB,DF⊥AB,∴∠OEC=∠OFD=90°,
又∵OC=OD,∴△COE≌△DOF(AAS),∴CE=DF.
12.解:连接OE,如图,
所对的圆心角为30°,∴∠COE=30°,
∵OC=OE,∴∠OCE=∠OEC,∴∠OCE=(180°-30°)÷2=75°,
∵弦CE∥AB,∴∠AOC=∠OCE=75°.
13.解:
理由:连接AE.
∴AB=AE,∴∠B=∠AEB,
∵四边形 ABCD 是平行四边形,∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,∴∠GAF=∠FAE,
14.解:四边形 OACB 是菱形.理由:
如图所示,连接OC.
∵C是 的中点,120°=60°.
∵CO=BO=AO,∴△OBC 是等边三角形,△OCA 是等边三角形,
∴OA=AC=BC=BO,∴四边形OACB 是菱形.
15.解:连接OD,OE,
的度数为40°,∴∠AOD=40°,
∵CD=CO,∴∠D=∠AOD=40°,
∵OD=OE,∴∠E=∠D=40°,∴∠DOE=180°-40°-40°=100°,
∴∠AOE=100°-40°=60°, 的度数是60°.
16.解:由题意知,在△OAB中,OA=OB=AB=r.
∴△OAB 为等边三角形.∴∠AOB=60°.∴弦AB 所对圆心角的度数为 60°.
17.证明:如图所示,连接OC.
∴∠AOC=∠BOC,即OC平分∠AOB,
∵CD⊥OA,CE⊥OB,∴CD=CE.
18.解:由题意,得. AB 的度数为 120°,∴∠AOB=120°.
如图所示,作OC⊥AB,垂足为 C,
∵OA=OB,
在 Rt△AOC中,AC= OA·sin60°= 4×
∴AB的长度为
19.解:延长 CO,交⊙O于点 E,连接 PE,如图所示.
∵OB=6,⊙O以点O为圆心,3为半径,∴OC=BC=OE=3,
∵∠AOB=90°,CD⊥OB,∴∠BCD=∠AOB=90°,AO垂直平分CE,
∴CD∥OA,CP=PE,∴△BCD∽△BOA,
∵OA=4,∴CD=2,∵CP=PE,∴PC+PD=PE+PD,
则要使 PC+PD的值最小,即 PE+PD 的值为最小,
∵PE+PD≥DE,∴当 D,P,E 三点共线时最小,
∴在 Rt△DCE中, ∴PC+PD的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
