第五章 圆 3 垂径定理(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
3 垂径定理
1.下列命题中正确的是 ( )
A.过弦的中点的直线垂直于弦,并且平分弦所对的弧 B.过弦的中点的直线必过圆心
C.平分弦的直径垂直于弦 D.垂直于弦且过圆心的直线平分弦所对的弧
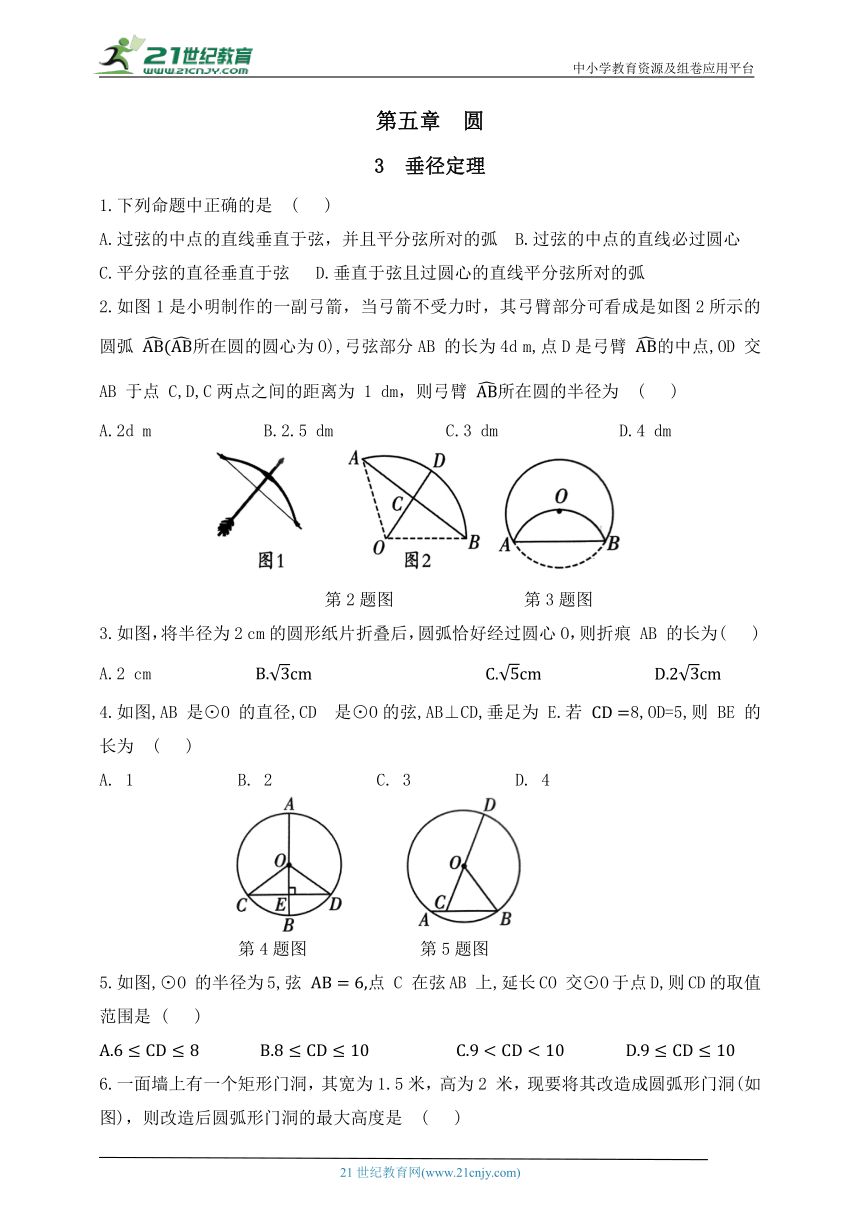
2.如图1是小明制作的一副弓箭,当弓箭不受力时,其弓臂部分可看成是如图2所示的圆弧 所在圆的圆心为O),弓弦部分AB 的长为4d m,点D是弓臂 的中点,OD 交 AB 于点 C,D,C两点之间的距离为 1 dm,则弓臂 所在圆的半径为 ( )
A.2d m B.2.5 dm C.3 dm D.4 dm
第2题图 第3题图
3.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕 AB 的长为( )
A.2 cm
4.如图,AB 是⊙O 的直径,CD 是⊙O的弦,AB⊥CD,垂足为 E.若 8,OD=5,则 BE 的长为 ( )
A. 1 B. 2 C. 3 D. 4
第4题图 第5题图
5.如图,⊙O 的半径为5,弦 点 C 在弦AB 上,延长CO 交⊙O于点D,则CD的取值范围是 ( )
6.一面墙上有一个矩形门洞,其宽为1.5米,高为2 米,现要将其改造成圆弧形门洞(如图),则改造后圆弧形门洞的最大高度是 ( )
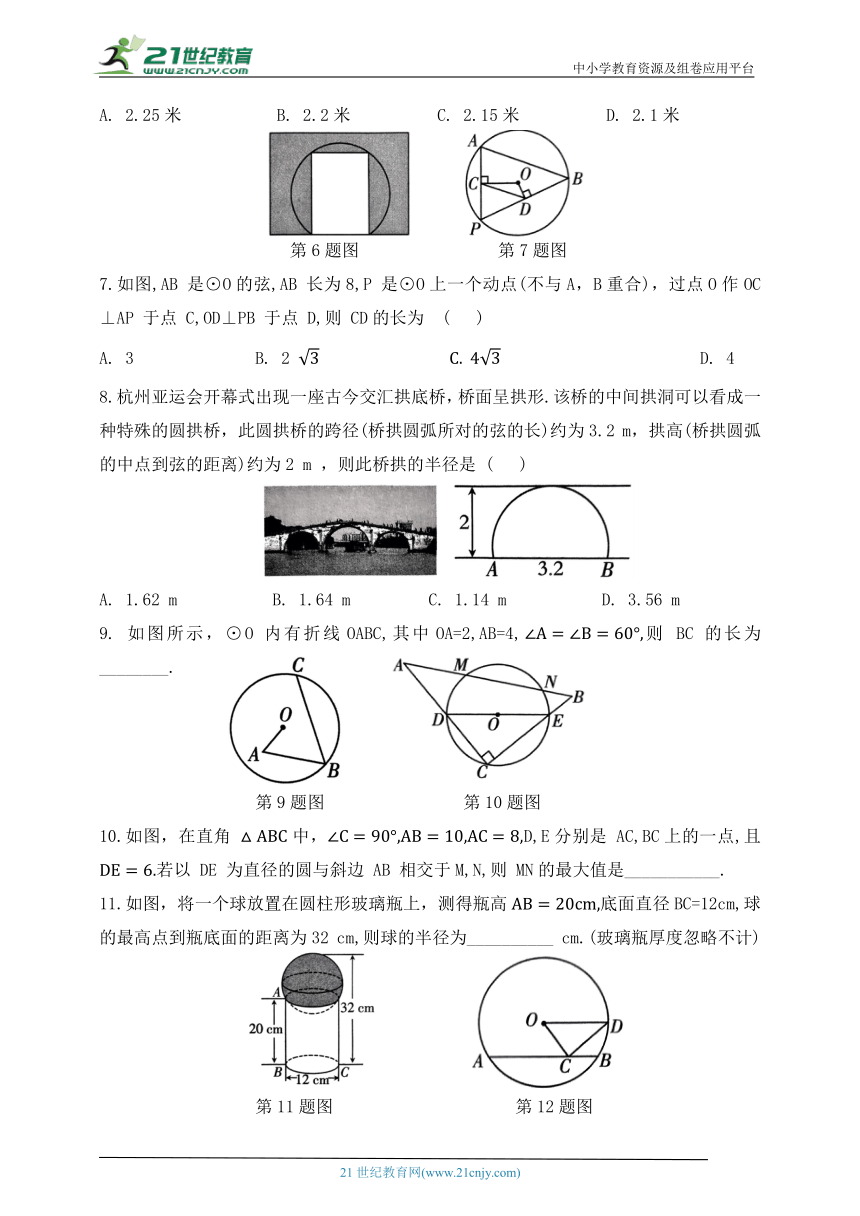
A. 2.25米 B. 2.2米 C. 2.15米 D. 2.1米
第6题图 第7题图
7.如图,AB 是⊙O的弦,AB 长为8,P 是⊙O上一个动点(不与A,B重合),过点O作OC⊥AP 于点 C,OD⊥PB 于点 D,则 CD的长为 ( )
A. 3 B. 2 D. 4
8.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2 m,拱高(桥拱圆弧的中点到弦的距离)约为2 m ,则此桥拱的半径是 ( )
A. 1.62 m B. 1.64 m C. 1.14 m D. 3.56 m
9. 如图所示,⊙O 内有折线OABC,其中OA=2,AB=4,则 BC 的长为________.
第9题图 第10题图
10.如图,在直角 中,D,E分别是 AC,BC上的一点,且若以 DE 为直径的圆与斜边 AB 相交于M,N,则 MN的最大值是___________.
11.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高底面直径BC=12cm,球的最高点到瓶底面的距离为32 cm,则球的半径为__________ cm.(玻璃瓶厚度忽略不计)
第11题图 第12题图
12.如图,在⊙O中,弦AB=4,点 C 在AB 上移动,连接OC,过点 C 作CD⊥OC,交⊙O于点D,则CD 长的最大值为__________.
13.如图,半径为5 的⊙A与y轴交于点B(0,2),C(0,10),则点A 的横坐标为__________.
14.已知AB,CD是⊙O 的两条平行弦, 24,CD=10,⊙O的半径为13,则弦AB与CD 的距离为_____________.
15.如图,在⊙O中,弦AB的长为8,点C在 BO延长线上,且
(1)求⊙O的半径;
(2)求 的正切值.
16.如图,一条公路的转弯处是一段圆弧 点O 是这段弧所在圆的圆心,点 C 是 的中点,点 D 是 AB 的中点,且则这段弯路所在圆的半径为多少
17.如图,⊙O的半径长为12cm,弦
(1)求圆心到弦 AB 的距离;
(2)如果弦AB 的两端点在圆周上滑动(AB弦长不变),那么弦AB的中点形成什么样的图形
18.如图,是一个半圆形桥洞的截面示意图,圆心为O,直径AB是河底截线,弦CD 是水位线,CD∥AB,于点E.
(1)当测得水面宽 时,求此时水位的高度OE;
(2)当水位的高度比(1)上升1m 时,有一艘宽为10m,船舱顶部高出水面2m 的货船要经过桥洞(船舱截面为矩形 MNPQ),请通过计算判断该货船能否顺利通过桥洞
19.已知:如图,AB 是⊙O 的弦, 点 C 是弦AB 上一动点(不与点 A,B重合),连接CO并延长交⊙O于点 D,连接AD.
(1)求弦AB的长;
(2)当 时,求 的度数;
(3)当AC 的长度为多少时,以A,C,D为顶点的三角形与以 B,O,C为顶点的三角形相似
参考答案
1. D 2. B 3. D 4. B 5. D 6. A 7. D 8. B
9. 6 10. 4.8 11. 7.5 12. 2 13. 3
14.7 或17 解析:如图1,当AB,CD 在点O 的两侧, 作 于点M,延长MO交 CD 于点 N,连接OA,OC,
∴此时弦AB与CD 之间的距离为17;
如图2,当AB,CD在点O的同侧,作 于点Q,交 AB 于 点 P,连接OA,OC,
∴此时弦AB与CD 之间的距离为7,
∴弦AB 与CD 之间的距离为 17 或7.
15.解:(1)过点O作 垂足为D,
∵AB=8,
在 中, ∴⊙O的半径为5;
(2)过点 C作( 垂足为E,
∥
在 中,
在 中, 的正切值为
16.解:连接OD,则点 O,C,D共线.
∵D是AB的中点,
设圆的半径为 rm,
在 中, 解得 r=25,
答:这段弯路所在圆的半径为25 m.
17.解:(1)作 垂足为C,连接AO,则
在 中,
即圆心到弦 AB 的距离是
(2)形成一个以O为圆心, 为半径的圆.(答“以O为圆心,OC 长为半径的圆”亦可)
18.解: (1)∵OE⊥CD,
又∴此时水位的高度
(2)该货船能顺利通过桥洞;
理由:由(1)中水位高度为 5m 可知此时
延长 OE 交 MQ 于 F,连接OM,则 MQ,
∵货船宽为10 m,船舱顶部高出水面2m,
货船居中行驶时
∴该货船能顺利通过桥洞.
19.解:(1)过点O作( 于点E,
∵在 中,
(2)连接OA,
∵OA=OB=OD,∠B=30°,∠D=20°,∴∠OAB=∠B=30°,∠OAD=∠D=20°,
∴∠AOC=40°,∠AOB=120°,∴∠COB=80°,∴∠DOB=100°;
(3)∵∠BCO=∠DAB+∠D,∴∠BCO>∠DAB,∠BCO>∠D,
∴要使△DAC与△BOC 相似,只能∠DCA=∠BCO=90°,
∴∠BOC=60°,∠BOD=120°,∴∠DAC=60°,∴△DAC∽△BOC,
∵∠BCO=90°,即OC⊥AB,
∴当 时,以A,C,D为顶点的三角形与以B,O,C为顶点的三角形相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
3 垂径定理
1.下列命题中正确的是 ( )
A.过弦的中点的直线垂直于弦,并且平分弦所对的弧 B.过弦的中点的直线必过圆心
C.平分弦的直径垂直于弦 D.垂直于弦且过圆心的直线平分弦所对的弧
2.如图1是小明制作的一副弓箭,当弓箭不受力时,其弓臂部分可看成是如图2所示的圆弧 所在圆的圆心为O),弓弦部分AB 的长为4d m,点D是弓臂 的中点,OD 交 AB 于点 C,D,C两点之间的距离为 1 dm,则弓臂 所在圆的半径为 ( )
A.2d m B.2.5 dm C.3 dm D.4 dm
第2题图 第3题图
3.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕 AB 的长为( )
A.2 cm
4.如图,AB 是⊙O 的直径,CD 是⊙O的弦,AB⊥CD,垂足为 E.若 8,OD=5,则 BE 的长为 ( )
A. 1 B. 2 C. 3 D. 4
第4题图 第5题图
5.如图,⊙O 的半径为5,弦 点 C 在弦AB 上,延长CO 交⊙O于点D,则CD的取值范围是 ( )
6.一面墙上有一个矩形门洞,其宽为1.5米,高为2 米,现要将其改造成圆弧形门洞(如图),则改造后圆弧形门洞的最大高度是 ( )
A. 2.25米 B. 2.2米 C. 2.15米 D. 2.1米
第6题图 第7题图
7.如图,AB 是⊙O的弦,AB 长为8,P 是⊙O上一个动点(不与A,B重合),过点O作OC⊥AP 于点 C,OD⊥PB 于点 D,则 CD的长为 ( )
A. 3 B. 2 D. 4
8.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2 m,拱高(桥拱圆弧的中点到弦的距离)约为2 m ,则此桥拱的半径是 ( )
A. 1.62 m B. 1.64 m C. 1.14 m D. 3.56 m
9. 如图所示,⊙O 内有折线OABC,其中OA=2,AB=4,则 BC 的长为________.
第9题图 第10题图
10.如图,在直角 中,D,E分别是 AC,BC上的一点,且若以 DE 为直径的圆与斜边 AB 相交于M,N,则 MN的最大值是___________.
11.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高底面直径BC=12cm,球的最高点到瓶底面的距离为32 cm,则球的半径为__________ cm.(玻璃瓶厚度忽略不计)
第11题图 第12题图
12.如图,在⊙O中,弦AB=4,点 C 在AB 上移动,连接OC,过点 C 作CD⊥OC,交⊙O于点D,则CD 长的最大值为__________.
13.如图,半径为5 的⊙A与y轴交于点B(0,2),C(0,10),则点A 的横坐标为__________.
14.已知AB,CD是⊙O 的两条平行弦, 24,CD=10,⊙O的半径为13,则弦AB与CD 的距离为_____________.
15.如图,在⊙O中,弦AB的长为8,点C在 BO延长线上,且
(1)求⊙O的半径;
(2)求 的正切值.
16.如图,一条公路的转弯处是一段圆弧 点O 是这段弧所在圆的圆心,点 C 是 的中点,点 D 是 AB 的中点,且则这段弯路所在圆的半径为多少
17.如图,⊙O的半径长为12cm,弦
(1)求圆心到弦 AB 的距离;
(2)如果弦AB 的两端点在圆周上滑动(AB弦长不变),那么弦AB的中点形成什么样的图形
18.如图,是一个半圆形桥洞的截面示意图,圆心为O,直径AB是河底截线,弦CD 是水位线,CD∥AB,于点E.
(1)当测得水面宽 时,求此时水位的高度OE;
(2)当水位的高度比(1)上升1m 时,有一艘宽为10m,船舱顶部高出水面2m 的货船要经过桥洞(船舱截面为矩形 MNPQ),请通过计算判断该货船能否顺利通过桥洞
19.已知:如图,AB 是⊙O 的弦, 点 C 是弦AB 上一动点(不与点 A,B重合),连接CO并延长交⊙O于点 D,连接AD.
(1)求弦AB的长;
(2)当 时,求 的度数;
(3)当AC 的长度为多少时,以A,C,D为顶点的三角形与以 B,O,C为顶点的三角形相似
参考答案
1. D 2. B 3. D 4. B 5. D 6. A 7. D 8. B
9. 6 10. 4.8 11. 7.5 12. 2 13. 3
14.7 或17 解析:如图1,当AB,CD 在点O 的两侧, 作 于点M,延长MO交 CD 于点 N,连接OA,OC,
∴此时弦AB与CD 之间的距离为17;
如图2,当AB,CD在点O的同侧,作 于点Q,交 AB 于 点 P,连接OA,OC,
∴此时弦AB与CD 之间的距离为7,
∴弦AB 与CD 之间的距离为 17 或7.
15.解:(1)过点O作 垂足为D,
∵AB=8,
在 中, ∴⊙O的半径为5;
(2)过点 C作( 垂足为E,
∥
在 中,
在 中, 的正切值为
16.解:连接OD,则点 O,C,D共线.
∵D是AB的中点,
设圆的半径为 rm,
在 中, 解得 r=25,
答:这段弯路所在圆的半径为25 m.
17.解:(1)作 垂足为C,连接AO,则
在 中,
即圆心到弦 AB 的距离是
(2)形成一个以O为圆心, 为半径的圆.(答“以O为圆心,OC 长为半径的圆”亦可)
18.解: (1)∵OE⊥CD,
又∴此时水位的高度
(2)该货船能顺利通过桥洞;
理由:由(1)中水位高度为 5m 可知此时
延长 OE 交 MQ 于 F,连接OM,则 MQ,
∵货船宽为10 m,船舱顶部高出水面2m,
货船居中行驶时
∴该货船能顺利通过桥洞.
19.解:(1)过点O作( 于点E,
∵在 中,
(2)连接OA,
∵OA=OB=OD,∠B=30°,∠D=20°,∴∠OAB=∠B=30°,∠OAD=∠D=20°,
∴∠AOC=40°,∠AOB=120°,∴∠COB=80°,∴∠DOB=100°;
(3)∵∠BCO=∠DAB+∠D,∴∠BCO>∠DAB,∠BCO>∠D,
∴要使△DAC与△BOC 相似,只能∠DCA=∠BCO=90°,
∴∠BOC=60°,∠BOD=120°,∴∠DAC=60°,∴△DAC∽△BOC,
∵∠BCO=90°,即OC⊥AB,
∴当 时,以A,C,D为顶点的三角形与以B,O,C为顶点的三角形相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
