第五章 圆 阶段性检测一(1~3节)(含答案)
文档属性
| 名称 | 第五章 圆 阶段性检测一(1~3节)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 16.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 19:25:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
阶段性检测一(1~3节)
1.下列说法中,正确的是 ( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.相等的圆心角所对的弦也相等
D.相等的弦所对的圆心角也相等
2.如图,以O为圆心的C,D三等分 连接MN,CD,下列结论错误的是 ( )
B.若 则 ∥
第2题图 第3题图
3.如图,在⊙O中,AB是⊙O的直径,AB=10,点 E 是点D关于AB的对称点, M是AB 上的一动点,下列结论:①∠BOE=30° ②∠DOB = 2∠CED ③DM⊥CE ④CM+DM 的最小值是 10.上述结论中正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
4.如图,圆形拱门最下端AB在地面上,D为AB的中点,C为拱门最高点,线段CD经过拱门所在圆的圆心,若 AB=1 m ,CD=2.5 m,则拱门所在圆的半径为 ( )
A. 1.25 m B. 1.3 m C.1.4 m D. 1.45 m
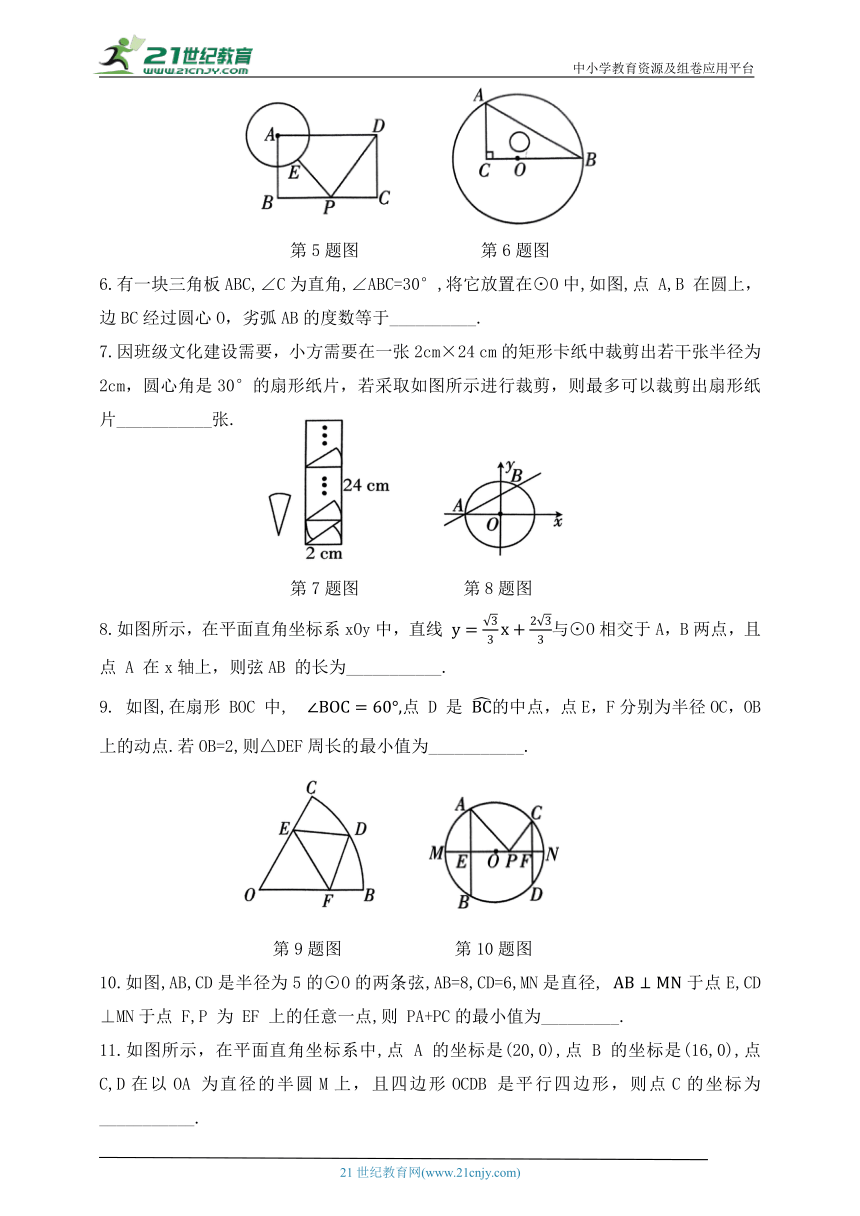
5.如图,在矩形 ABCD 中, 以A为圆心,2为半径画圆A,E是圆A 上一动点,P是 BC 上一动点,则 最小值是 ( )
第5题图 第6题图
6.有一块三角板ABC,∠C为直角,∠ABC=30°,将它放置在⊙O中,如图,点 A,B 在圆上,边BC经过圆心O,劣弧AB的度数等于__________.
7.因班级文化建设需要,小方需要在一张2cm×24 cm的矩形卡纸中裁剪出若干张半径为2cm,圆心角是30°的扇形纸片,若采取如图所示进行裁剪,则最多可以裁剪出扇形纸片___________张.
第7题图 第8题图
8.如图所示,在平面直角坐标系xOy中,直线 与⊙O相交于A,B两点,且点 A 在x轴上,则弦AB 的长为___________.
9. 如图,在扇形 BOC 中, 点 D 是 的中点,点E,F分别为半径OC,OB上的动点.若OB=2,则△DEF周长的最小值为___________.
第9题图 第10题图
10.如图,AB,CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径, 于点E,CD⊥MN于点 F,P 为 EF 上的任意一点,则 PA+PC的最小值为_________.
11.如图所示,在平面直角坐标系中,点 A 的坐标是(20,0),点 B 的坐标是(16,0),点 C,D在以OA 为直径的半圆M上,且四边形OCDB 是平行四边形,则点C的坐标为___________.
12.如图,⊙O 的直径AB 垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接 BC,作 OF⊥BC 于点 F,求 OF的长.
13.如图所示,该小组发现 8米高旗杆DE的影子EF 落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,同一时刻测得其影长为2.4米,同时测得 EG的长为3米,HF的长为1米,测得拱高(弧GH 的中点到弦GH 的距离,即 MN 的长)为2米,求小桥所在圆的半径.
14.如图,已知 B在反比例函数 上,以AB为直径的圆的圆心C在y轴上,⊙C与y轴正半轴交于 D(0,4).求k的值.
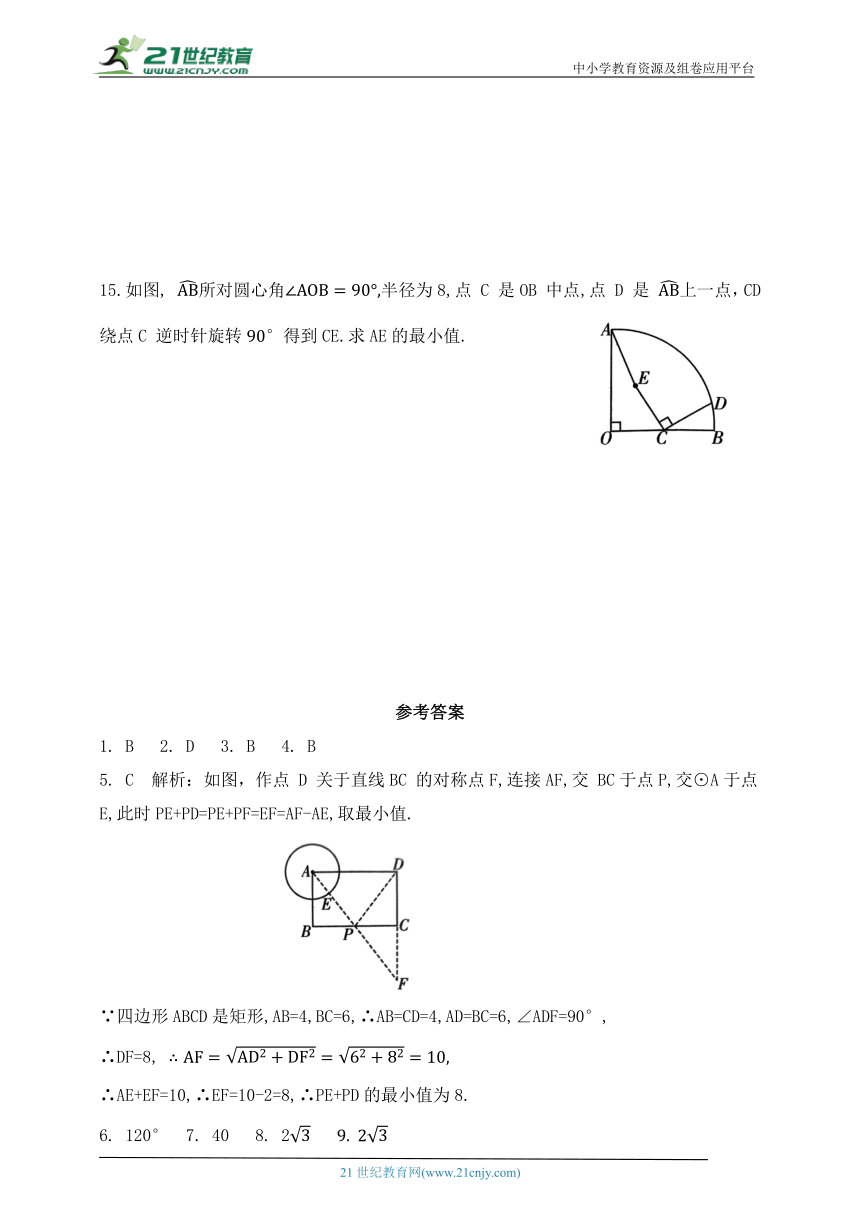
15.如图, 所对圆心角半径为8,点 C 是OB 中点,点 D 是 上一点,CD 绕点C 逆时针旋转得到CE.求AE的最小值.
参考答案
1. B 2. D 3. B 4. B
5. C 解析:如图,作点 D 关于直线BC 的对称点F,连接AF,交 BC于点P,交⊙A于点E,此时PE+PD=PE+PF=EF=AF-AE,取最小值.
∵四边形ABCD是矩形,AB=4,BC=6,∴AB=CD=4,AD=BC=6,∠ADF=90°,
∴DF=8,
∴AE+EF=10,∴EF=10-2=8,∴PE+PD的最小值为8.
6. 120° 7. 40 8. 2
解析:连接OB,OC,BC,作CH⊥AB于点 H.
根据垂径定理得到
∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH 中,根据勾股定理得到 BC= 则 PA+PC的最小值为
11.(2,6) 解析:∵四边形OCDB是平行四边形,B(16,0),∴CD∥OA,CD=OB=16.
过点 M 作MF⊥CD于点F,则 过点C作CE⊥OA 于点E,
∵A(20,0),∴OA=20,OM=10,∴OE = OM - ME =OM-CF=10-8=2.
连接MC,则
∴在 Rt△CMF中,由勾股定理,得
∴点C的坐标为(2,6).
12.解:(1)连接OD,如图,设⊙O的半径长为r,
∵AB⊥CD, 8=4,
在Rt△ODE中,OE=r-2,OD=r,DE=4,
由勾股定理,得 即 解得r=5,即⊙O的半径长为5;
(2)在 Rt△BCE中,∵CE=4,BE = AB-AE=2×5-2=8,
∵OF⊥BC,
在 Rt△OBF 中, 即OF 的长为
13.解:∵小刚身高 1.6米,同一时刻测得其影长为2.4 米,
∴8米高旗杆 DE 的影子为12m,
∵测得 EG的长为3米,HF 的长为1米,
如图,设小桥的圆心为O,连接OM,OG.
设小桥所在圆的半径为r,
在 中,由勾股定理,得
解得r=5,
答:小桥所在圆的半径为5m.
14.解:设⊙C与x轴的正半轴的交点为E,连接BE,
∵OC⊥AE,A(-2,0),∴OA=OE=2,
∵以 AB 为直径的圆的圆心C在y轴上,D(0,4),∴CA=CB,OD=4,
∴OC是△ABE的中位线,
∵CO⊥x轴,∴BE⊥x轴,
设OC=x,则AC=CD=4-x,BE=2x,
在 Rt△ACO中, 解得
∴BE=2x=3,∴B(2,3),∴k=2×3=6.
15.解:如图,连接OD,以OC为边向下作正方形OCTH,连接AT,ET.
在 和 中,
∴AE 的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
阶段性检测一(1~3节)
1.下列说法中,正确的是 ( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.相等的圆心角所对的弦也相等
D.相等的弦所对的圆心角也相等
2.如图,以O为圆心的C,D三等分 连接MN,CD,下列结论错误的是 ( )
B.若 则 ∥
第2题图 第3题图
3.如图,在⊙O中,AB是⊙O的直径,AB=10,点 E 是点D关于AB的对称点, M是AB 上的一动点,下列结论:①∠BOE=30° ②∠DOB = 2∠CED ③DM⊥CE ④CM+DM 的最小值是 10.上述结论中正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
4.如图,圆形拱门最下端AB在地面上,D为AB的中点,C为拱门最高点,线段CD经过拱门所在圆的圆心,若 AB=1 m ,CD=2.5 m,则拱门所在圆的半径为 ( )
A. 1.25 m B. 1.3 m C.1.4 m D. 1.45 m
5.如图,在矩形 ABCD 中, 以A为圆心,2为半径画圆A,E是圆A 上一动点,P是 BC 上一动点,则 最小值是 ( )
第5题图 第6题图
6.有一块三角板ABC,∠C为直角,∠ABC=30°,将它放置在⊙O中,如图,点 A,B 在圆上,边BC经过圆心O,劣弧AB的度数等于__________.
7.因班级文化建设需要,小方需要在一张2cm×24 cm的矩形卡纸中裁剪出若干张半径为2cm,圆心角是30°的扇形纸片,若采取如图所示进行裁剪,则最多可以裁剪出扇形纸片___________张.
第7题图 第8题图
8.如图所示,在平面直角坐标系xOy中,直线 与⊙O相交于A,B两点,且点 A 在x轴上,则弦AB 的长为___________.
9. 如图,在扇形 BOC 中, 点 D 是 的中点,点E,F分别为半径OC,OB上的动点.若OB=2,则△DEF周长的最小值为___________.
第9题图 第10题图
10.如图,AB,CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径, 于点E,CD⊥MN于点 F,P 为 EF 上的任意一点,则 PA+PC的最小值为_________.
11.如图所示,在平面直角坐标系中,点 A 的坐标是(20,0),点 B 的坐标是(16,0),点 C,D在以OA 为直径的半圆M上,且四边形OCDB 是平行四边形,则点C的坐标为___________.
12.如图,⊙O 的直径AB 垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接 BC,作 OF⊥BC 于点 F,求 OF的长.
13.如图所示,该小组发现 8米高旗杆DE的影子EF 落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,同一时刻测得其影长为2.4米,同时测得 EG的长为3米,HF的长为1米,测得拱高(弧GH 的中点到弦GH 的距离,即 MN 的长)为2米,求小桥所在圆的半径.
14.如图,已知 B在反比例函数 上,以AB为直径的圆的圆心C在y轴上,⊙C与y轴正半轴交于 D(0,4).求k的值.
15.如图, 所对圆心角半径为8,点 C 是OB 中点,点 D 是 上一点,CD 绕点C 逆时针旋转得到CE.求AE的最小值.
参考答案
1. B 2. D 3. B 4. B
5. C 解析:如图,作点 D 关于直线BC 的对称点F,连接AF,交 BC于点P,交⊙A于点E,此时PE+PD=PE+PF=EF=AF-AE,取最小值.
∵四边形ABCD是矩形,AB=4,BC=6,∴AB=CD=4,AD=BC=6,∠ADF=90°,
∴DF=8,
∴AE+EF=10,∴EF=10-2=8,∴PE+PD的最小值为8.
6. 120° 7. 40 8. 2
解析:连接OB,OC,BC,作CH⊥AB于点 H.
根据垂径定理得到
∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH 中,根据勾股定理得到 BC= 则 PA+PC的最小值为
11.(2,6) 解析:∵四边形OCDB是平行四边形,B(16,0),∴CD∥OA,CD=OB=16.
过点 M 作MF⊥CD于点F,则 过点C作CE⊥OA 于点E,
∵A(20,0),∴OA=20,OM=10,∴OE = OM - ME =OM-CF=10-8=2.
连接MC,则
∴在 Rt△CMF中,由勾股定理,得
∴点C的坐标为(2,6).
12.解:(1)连接OD,如图,设⊙O的半径长为r,
∵AB⊥CD, 8=4,
在Rt△ODE中,OE=r-2,OD=r,DE=4,
由勾股定理,得 即 解得r=5,即⊙O的半径长为5;
(2)在 Rt△BCE中,∵CE=4,BE = AB-AE=2×5-2=8,
∵OF⊥BC,
在 Rt△OBF 中, 即OF 的长为
13.解:∵小刚身高 1.6米,同一时刻测得其影长为2.4 米,
∴8米高旗杆 DE 的影子为12m,
∵测得 EG的长为3米,HF 的长为1米,
如图,设小桥的圆心为O,连接OM,OG.
设小桥所在圆的半径为r,
在 中,由勾股定理,得
解得r=5,
答:小桥所在圆的半径为5m.
14.解:设⊙C与x轴的正半轴的交点为E,连接BE,
∵OC⊥AE,A(-2,0),∴OA=OE=2,
∵以 AB 为直径的圆的圆心C在y轴上,D(0,4),∴CA=CB,OD=4,
∴OC是△ABE的中位线,
∵CO⊥x轴,∴BE⊥x轴,
设OC=x,则AC=CD=4-x,BE=2x,
在 Rt△ACO中, 解得
∴BE=2x=3,∴B(2,3),∴k=2×3=6.
15.解:如图,连接OD,以OC为边向下作正方形OCTH,连接AT,ET.
在 和 中,
∴AE 的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
