第五章 圆 4 圆周角和圆心角的关系 第1课时 圆周角订立及其推论1,2(含答案)
文档属性
| 名称 | 第五章 圆 4 圆周角和圆心角的关系 第1课时 圆周角订立及其推论1,2(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 19:31:43 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 圆
4 圆周角和圆心角的关系
第1课时 圆周角订立及其推论1,2
1.下列命题中,属于真命题的是 ( )
A.在同圆中,同一条弦所对的圆周角相等 B.相等的圆周角所对的弧长度相等
C.等弧所对的圆周角相等 D.长度相等的弧所对的圆周角相等
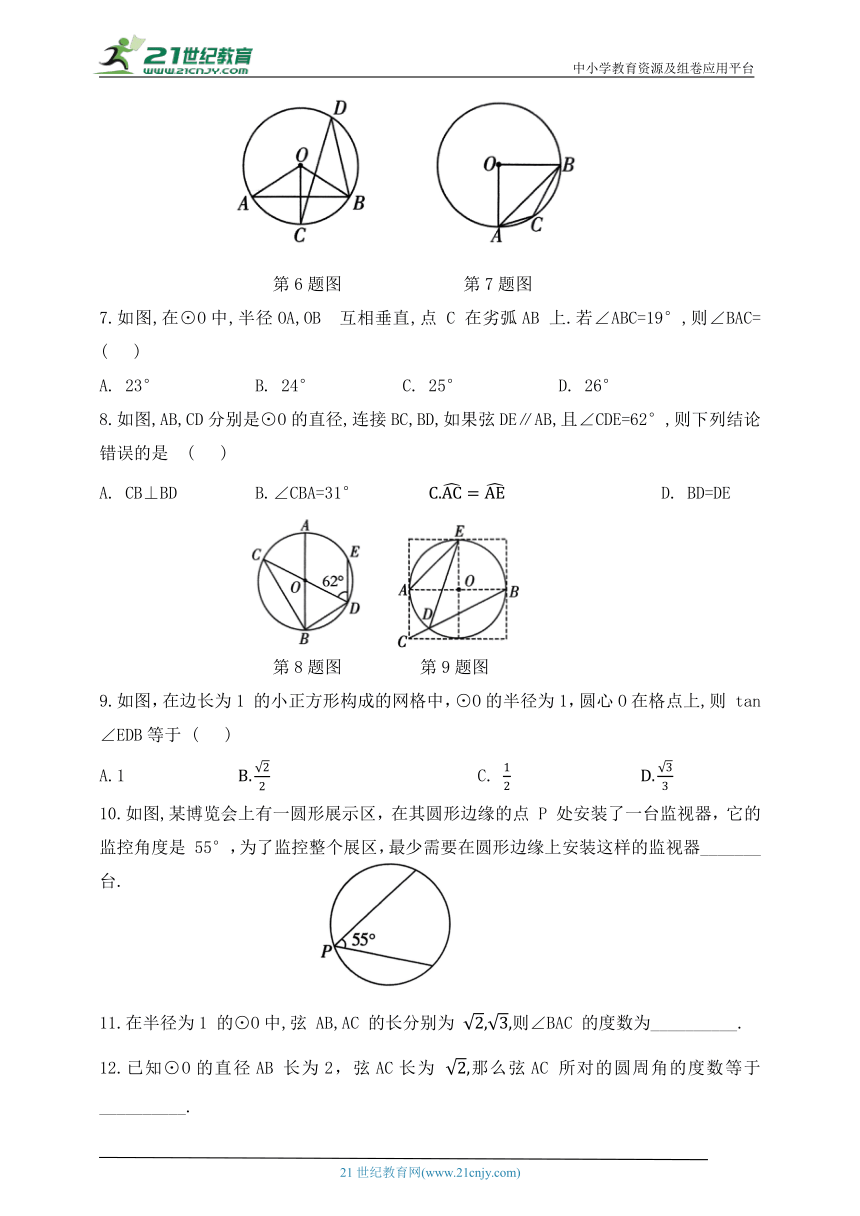
2.如图,四边形 ABCD 的四个顶点都在⊙O 上,AB=CD,连接OA,OC.若∠BAD=80°,则∠AOC 的度数为 ( )
A.100° B.160° C.120° D.135°
第2题图 第3题图
3.如图所示, 点C在⊙O上,且点 C不与A,B重合,则∠ACB的度数是( )
A. 50° B. 80°或50° C. 130° D. 50°或130°
4.如图,AD 是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点 E,∠BOC=42°,则∠OED的度数是 ( )
A. 61° B. 63° C. 65° D. 67°
第4题图 第5题图
5.如图,AC,BC为⊙O的两条弦,D,G分别为AC,BC的中点,⊙O的半径为2.若 则 DG的长为 ( )
A. 2
6.如图,AB是⊙O 的弦, AB 交⊙O于点C,点 D 是⊙O上一点,连接BD,CD.若∠D=28°,则∠OAB 的度数为 ( )
A. 28° B. 34° C. 56°
第6题图 第7题图
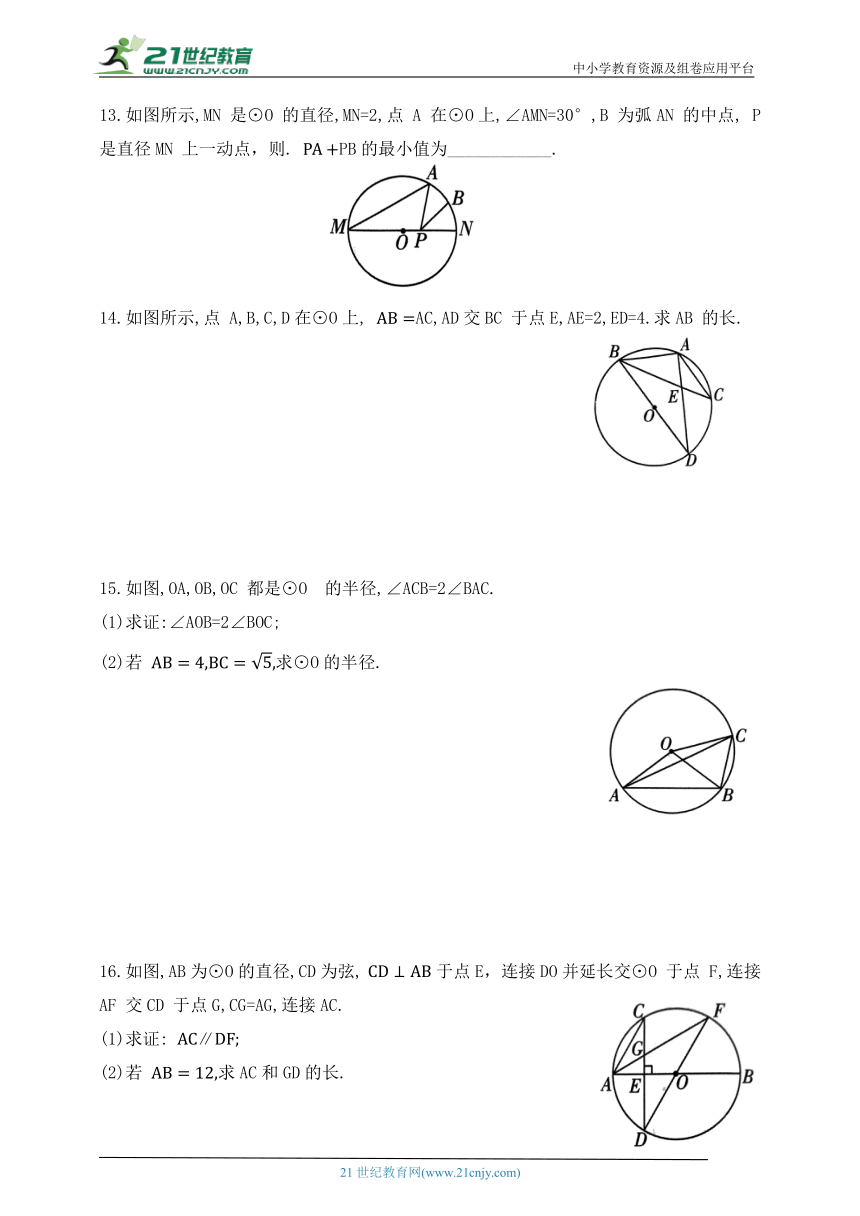
7.如图,在⊙O中,半径OA,OB 互相垂直,点 C 在劣弧AB 上.若∠ABC=19°,则∠BAC= ( )
A. 23° B. 24° C. 25° D. 26°
8.如图,AB,CD分别是⊙O的直径,连接BC,BD,如果弦DE∥AB,且∠CDE=62°,则下列结论错误的是 ( )
A. CB⊥BD B.∠CBA=31° D. BD=DE
第8题图 第9题图
9.如图,在边长为1 的小正方形构成的网格中,⊙O的半径为1,圆心O在格点上,则 tan∠EDB等于 ( )
A.1 C.
10.如图,某博览会上有一圆形展示区,在其圆形边缘的点 P 处安装了一台监视器,它的监控角度是 55°,为了监控整个展区,最少需要在圆形边缘上安装这样的监视器_______台.
11.在半径为1 的⊙O中,弦 AB,AC 的长分别为 则∠BAC 的度数为__________.
12.已知⊙O的直径AB 长为2,弦AC长为 那么弦AC 所对的圆周角的度数等于__________.
13.如图所示,MN 是⊙O 的直径,MN=2,点 A 在⊙O上,∠AMN=30°,B 为弧AN 的中点, P 是直径MN 上一动点,则. PB的最小值为____________.
14.如图所示,点 A,B,C,D在⊙O上, AC,AD交BC 于点E,AE=2,ED=4.求AB 的长.
15.如图,OA,OB,OC 都是⊙O 的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若 求⊙O的半径.
16.如图,AB为⊙O的直径,CD为弦, 于点E,连接DO并延长交⊙O 于点 F,连接 AF 交CD 于点G,CG=AG,连接AC.
(1)求证: ∥
(2)若 求AC和GD的长.
17.如图,AB 是⊙O 的直径,BC,BD是⊙O的两条弦,点 C 与点 D 在AB 的两侧,E 是OB 上一点连接OC,CE,且∠BOC=2∠BCE.
(1)如图1,若 求⊙O 的半径;
(2)如图2,若 求证:∥(请用两种证法解答)
参考答案
1. C 2. B 3. D 4. B 5. D 6. B 7. D 8. D 9. A
10. 4 或 12. 45°或
14.解:
又
∵∠BAE=∠DAB,∴
=6×2=12.
15.解:(1)证明:∵∠BOC=2∠BAC,∠ACB=2∠BAC,∴∠BOC=∠ACB,
又∵∠AOB=2∠ACB,∴∠AOB=2∠BOC;
(2)过点 O 作半径OD⊥AB 于点 E,连接BD,
∴AE=BE,∠AOB=2∠DOB,
∵∠AOB=2∠BOC,∴∠DOB=∠BOC,∴BD=BC.
在 Rt△BDE 中,∠DEB=90°,
在 Rt△BOE 中,∠OEB=90°, 解得 即⊙O的半径是
16.解:(1)证明:∵AG=CG,∴∠DCA=∠CAF,
∴∠CAF=∠CDF,∴∠ACD=∠CDF,∴AC∥DF;
(2)如图,连接CO,
∵AB⊥CD,
∵∠DCA=∠CAF, ∴∠AOD=∠AOC=∠COF,
∵DF 是直径,∴∠AOD=∠AOC=∠COF=60°,
∵OA=OC,∴△AOC是等边三角形,∴AC=AO=6,∠CAO=60°,
∵CE⊥AO,∴AE=EO=3,∠ACD=30°,
17.解:(1)如图1,过点O作OH⊥BC于点 H.
∵OC=OB,OH⊥BC,∴∠COH=∠BOH,CH=BH,
∵∠BOC=2∠BCE,∴∠BOH=∠BCE,
∵∠BOH+∠OBH=90°,∴∠BCE+∠OBH=90°,∴∠CEB=90°,
∴OB=3,∴⊙O的半径为3;
(2)证法一:如图2,过点O作OK⊥BD于点 K,则 BK=DK,
∵BD=2OE,∴OE=BK,
由(1)得∠CEB=90°,∴∠CEO=∠OKB=90°,又∵OC=OB,∴Rt△OEC≌Rt△BKO(HL),
∴∠COE=∠OBK,∴OC∥BD;
证法二:如图2,过点O作OK⊥BD于点K,则 BK=DK,
∵BD=2OE,∴OE=BK,
∴cos∠COE=cos∠OBK,
∴∠COE=∠OBK,∴OC∥BD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
4 圆周角和圆心角的关系
第1课时 圆周角订立及其推论1,2
1.下列命题中,属于真命题的是 ( )
A.在同圆中,同一条弦所对的圆周角相等 B.相等的圆周角所对的弧长度相等
C.等弧所对的圆周角相等 D.长度相等的弧所对的圆周角相等
2.如图,四边形 ABCD 的四个顶点都在⊙O 上,AB=CD,连接OA,OC.若∠BAD=80°,则∠AOC 的度数为 ( )
A.100° B.160° C.120° D.135°
第2题图 第3题图
3.如图所示, 点C在⊙O上,且点 C不与A,B重合,则∠ACB的度数是( )
A. 50° B. 80°或50° C. 130° D. 50°或130°
4.如图,AD 是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点 E,∠BOC=42°,则∠OED的度数是 ( )
A. 61° B. 63° C. 65° D. 67°
第4题图 第5题图
5.如图,AC,BC为⊙O的两条弦,D,G分别为AC,BC的中点,⊙O的半径为2.若 则 DG的长为 ( )
A. 2
6.如图,AB是⊙O 的弦, AB 交⊙O于点C,点 D 是⊙O上一点,连接BD,CD.若∠D=28°,则∠OAB 的度数为 ( )
A. 28° B. 34° C. 56°
第6题图 第7题图
7.如图,在⊙O中,半径OA,OB 互相垂直,点 C 在劣弧AB 上.若∠ABC=19°,则∠BAC= ( )
A. 23° B. 24° C. 25° D. 26°
8.如图,AB,CD分别是⊙O的直径,连接BC,BD,如果弦DE∥AB,且∠CDE=62°,则下列结论错误的是 ( )
A. CB⊥BD B.∠CBA=31° D. BD=DE
第8题图 第9题图
9.如图,在边长为1 的小正方形构成的网格中,⊙O的半径为1,圆心O在格点上,则 tan∠EDB等于 ( )
A.1 C.
10.如图,某博览会上有一圆形展示区,在其圆形边缘的点 P 处安装了一台监视器,它的监控角度是 55°,为了监控整个展区,最少需要在圆形边缘上安装这样的监视器_______台.
11.在半径为1 的⊙O中,弦 AB,AC 的长分别为 则∠BAC 的度数为__________.
12.已知⊙O的直径AB 长为2,弦AC长为 那么弦AC 所对的圆周角的度数等于__________.
13.如图所示,MN 是⊙O 的直径,MN=2,点 A 在⊙O上,∠AMN=30°,B 为弧AN 的中点, P 是直径MN 上一动点,则. PB的最小值为____________.
14.如图所示,点 A,B,C,D在⊙O上, AC,AD交BC 于点E,AE=2,ED=4.求AB 的长.
15.如图,OA,OB,OC 都是⊙O 的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若 求⊙O的半径.
16.如图,AB为⊙O的直径,CD为弦, 于点E,连接DO并延长交⊙O 于点 F,连接 AF 交CD 于点G,CG=AG,连接AC.
(1)求证: ∥
(2)若 求AC和GD的长.
17.如图,AB 是⊙O 的直径,BC,BD是⊙O的两条弦,点 C 与点 D 在AB 的两侧,E 是OB 上一点连接OC,CE,且∠BOC=2∠BCE.
(1)如图1,若 求⊙O 的半径;
(2)如图2,若 求证:∥(请用两种证法解答)
参考答案
1. C 2. B 3. D 4. B 5. D 6. B 7. D 8. D 9. A
10. 4 或 12. 45°或
14.解:
又
∵∠BAE=∠DAB,∴
=6×2=12.
15.解:(1)证明:∵∠BOC=2∠BAC,∠ACB=2∠BAC,∴∠BOC=∠ACB,
又∵∠AOB=2∠ACB,∴∠AOB=2∠BOC;
(2)过点 O 作半径OD⊥AB 于点 E,连接BD,
∴AE=BE,∠AOB=2∠DOB,
∵∠AOB=2∠BOC,∴∠DOB=∠BOC,∴BD=BC.
在 Rt△BDE 中,∠DEB=90°,
在 Rt△BOE 中,∠OEB=90°, 解得 即⊙O的半径是
16.解:(1)证明:∵AG=CG,∴∠DCA=∠CAF,
∴∠CAF=∠CDF,∴∠ACD=∠CDF,∴AC∥DF;
(2)如图,连接CO,
∵AB⊥CD,
∵∠DCA=∠CAF, ∴∠AOD=∠AOC=∠COF,
∵DF 是直径,∴∠AOD=∠AOC=∠COF=60°,
∵OA=OC,∴△AOC是等边三角形,∴AC=AO=6,∠CAO=60°,
∵CE⊥AO,∴AE=EO=3,∠ACD=30°,
17.解:(1)如图1,过点O作OH⊥BC于点 H.
∵OC=OB,OH⊥BC,∴∠COH=∠BOH,CH=BH,
∵∠BOC=2∠BCE,∴∠BOH=∠BCE,
∵∠BOH+∠OBH=90°,∴∠BCE+∠OBH=90°,∴∠CEB=90°,
∴OB=3,∴⊙O的半径为3;
(2)证法一:如图2,过点O作OK⊥BD于点 K,则 BK=DK,
∵BD=2OE,∴OE=BK,
由(1)得∠CEB=90°,∴∠CEO=∠OKB=90°,又∵OC=OB,∴Rt△OEC≌Rt△BKO(HL),
∴∠COE=∠OBK,∴OC∥BD;
证法二:如图2,过点O作OK⊥BD于点K,则 BK=DK,
∵BD=2OE,∴OE=BK,
∴cos∠COE=cos∠OBK,
∴∠COE=∠OBK,∴OC∥BD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
