第五章 圆 5 确定圆的条件 第1课时 确定圆的条件(含答案)
文档属性
| 名称 | 第五章 圆 5 确定圆的条件 第1课时 确定圆的条件(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 圆
5 确定圆的条件
第1课时 确定圆的条件
1.下列条件中,能确定圆的是 ( )
A.以已知点O为圆心 B.以1 cm长为半径
C.经过已知点 A,且半径为2cm D.以点O为圆心,1 cm为半径
2.下列说法中正确的是 ( )
①过A,B,C三点一定可以确定一个圆 ②锐角三角形的外心在三角形的内部 ③过A,B两点一定可以作一个且只能作一个圆 ④三角形的外心到三角形各顶点的距离相等
A.①② B.①③ C.②④ D.②③
3.如图,在 的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是 ( )
A.点 P B.点 Q C.点 R D.点 M
第3题图 第4题图
4.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是 ( )
A.① B.② C.③ D.均不可能
5.若点 O是 的外心,且 则∠BAC的度数为 ( )
或 或
6.如图,点 A,B,C均在直线上,点P 在直线l 外,则经过其中任意三个点,最多可画出圆的个数为 ( )
A.1个 B.2个 C.3个 D.4个
7.已知 M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下 P 点坐标不满足要求的是 ( )
8.如图的方格纸中,每个方格的边长为1,A,O 两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点 B,C,使得 的外心为O,求BC 的长度为___________.
9.如图, 内接于⊙O,圆的半径为7, 则弦 BC 的长度为___________.
第9题图 第10题图
10.如图, 则 的大小是___________.
11. 如图所示, 内接于⊙O,AD 是的边 BC 上的高,AE 是⊙O 的直径,连接 BE, 与 相似吗 请证明你的结论.
12.如图,⊙O是 的外接圆,D 是直径AB 上一点, 的平分线交AB 于点E,交⊙O于另一点 F, FE.
(1)求证:
(2)设 垂足为M,若1,求AC的长.
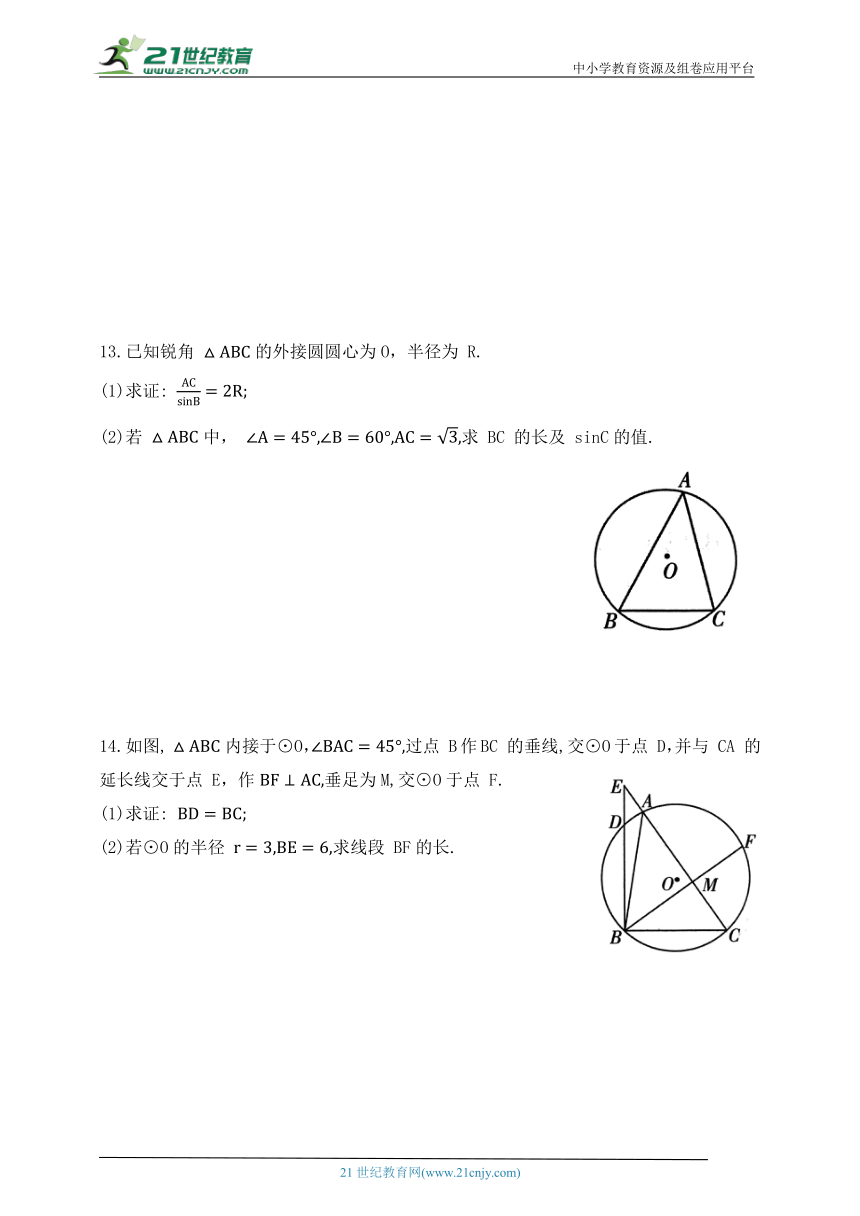
13.已知锐角 的外接圆圆心为O,半径为 R.
(1)求证:
(2)若 中, 求 BC 的长及 sinC的值.
14.如图, 内接于⊙O,过点 B作BC 的垂线,交⊙O于点 D,并与 CA 的延长线交于点 E,作垂足为M,交⊙O于点 F.
(1)求证:
(2)若⊙O的半径 求线段 BF的长.
15.如图,在 中,D 为 AB 中点, ⊙O是 的外接圆.
(1)求 BC的长;
(2)求⊙O的半径.
16.定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图1,在损矩形 ABCD 中,∠ABC=则该损矩形的直径是线段__________;
(2)在线段AC上确定一点 P,使损矩形的四个顶点都在以 P 为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由(友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹);
(3)如图2,在 中, 以AC为一边向三角形外作菱形ACEF,D为菱形 ACEF的中心,连接 BD,当 BD平分时,判断四边形ACEF 为何种特殊的四边形 请说明理由.若此时 求 BC的长.
参考答案
1. D 2. C 3. B 4. A 5. C 6. C 7. C
10. 30°
11.解:△ABE∽△ADC.
证明:∵AE是⊙O的直径,∴∠ABE=90°.
∵AD 是△ABC的边 BC 上的高,∴∠ADC=90°.∴∠ADC=∠ABE=90°.
又∵∠C=∠E,∴△ABE∽△ADC.
12.解:(1)证明:∵FA=FE,∴∠FAE=∠AEF.
∵∠FAE与∠BCE都是 所对的圆周角,∴∠FAE=∠BCE.
∵∠AEF=∠CEB,∴∠CEB=∠BCE.
∵CE平分∠ACD,∴∠ACE=∠DCE.
∵AB是直径,∴∠ACB=90°,∴∠CEB+∠DCE=∠BCE +∠ACE=∠ACB=90°,
∴∠CDE=90°,∴CD⊥AB;
(2)由(1)知,∠BEC=∠BCE,∴BE=BC.
∵AF=EF,FM⊥AB,∴MA=ME=2,AE=4.∴圆的半径(
在 中,
13.解:(1)证明:如图1所示,连接AO并延长, 交⊙O于点D,连接CD.
则
同理,
如图2所示,过点 C作 于点E.
14.解:(1)证明:如图,连接DC,则∠BDC=∠BAC=45°,
∵BD⊥BC,∴∠BCD=90°-∠BDC=45°,∴∠BCD=∠BDC,∴BD=BC;
(2)如图,∵∠DBC=90°,∴CD为⊙O的直径.∴CD=2r=6.
∵BF⊥AC,∴∠BMC=∠EBC=90°,
又∵∠BCM=∠BCE.∴△BCM∽△ECB,
连接CF,则∠F=∠BAC=45°,∠MCF=90°-45°=45°,
15.解:
D为AB 中点,
(2)过点 A 作 于点 E,连接CO并延长,交⊙O于点 F,连接AF,
∵在 中,
∴DE=1,
∵△BAC∽△BCD,
设CD=x,则
∵在Rt△ACE 中,
即 解得. (舍去),
∵∠AFC与 都是 所对的圆周角,∴∠AFC=∠ADC.
∵CF为⊙O的直径,
即⊙O的半径为
16.解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此 AC 是该损矩形的直径;故答案为:AC;
(2)作图如图1:
∵点 P 为AC 中点,
∴点A,B,C,D在以P 为圆心, 为半径的同一个圆上;
(3)∵四边形ACEF 为菱形,∴∠ADC=90°,AE=2AD,CF=2CD.
∴四边形 ABCD为损矩形.∴由(2)可知,点 A,B,C,D在同一个圆上.
∵BD平分∠ABC,∴∠ABD=∠CBD=45°.
∴AD=CD.∴AE=CF.∴四边形 ACEF为正方形.过点 D作DM⊥AB,DN⊥BC,如图2.
∵∠ABD=∠CBD=45°,BD=4 ,∴DM=BN=4,
S△BCD,
∴BC=5或BC=-3(舍去).∴BC=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
5 确定圆的条件
第1课时 确定圆的条件
1.下列条件中,能确定圆的是 ( )
A.以已知点O为圆心 B.以1 cm长为半径
C.经过已知点 A,且半径为2cm D.以点O为圆心,1 cm为半径
2.下列说法中正确的是 ( )
①过A,B,C三点一定可以确定一个圆 ②锐角三角形的外心在三角形的内部 ③过A,B两点一定可以作一个且只能作一个圆 ④三角形的外心到三角形各顶点的距离相等
A.①② B.①③ C.②④ D.②③
3.如图,在 的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是 ( )
A.点 P B.点 Q C.点 R D.点 M
第3题图 第4题图
4.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是 ( )
A.① B.② C.③ D.均不可能
5.若点 O是 的外心,且 则∠BAC的度数为 ( )
或 或
6.如图,点 A,B,C均在直线上,点P 在直线l 外,则经过其中任意三个点,最多可画出圆的个数为 ( )
A.1个 B.2个 C.3个 D.4个
7.已知 M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下 P 点坐标不满足要求的是 ( )
8.如图的方格纸中,每个方格的边长为1,A,O 两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点 B,C,使得 的外心为O,求BC 的长度为___________.
9.如图, 内接于⊙O,圆的半径为7, 则弦 BC 的长度为___________.
第9题图 第10题图
10.如图, 则 的大小是___________.
11. 如图所示, 内接于⊙O,AD 是的边 BC 上的高,AE 是⊙O 的直径,连接 BE, 与 相似吗 请证明你的结论.
12.如图,⊙O是 的外接圆,D 是直径AB 上一点, 的平分线交AB 于点E,交⊙O于另一点 F, FE.
(1)求证:
(2)设 垂足为M,若1,求AC的长.
13.已知锐角 的外接圆圆心为O,半径为 R.
(1)求证:
(2)若 中, 求 BC 的长及 sinC的值.
14.如图, 内接于⊙O,过点 B作BC 的垂线,交⊙O于点 D,并与 CA 的延长线交于点 E,作垂足为M,交⊙O于点 F.
(1)求证:
(2)若⊙O的半径 求线段 BF的长.
15.如图,在 中,D 为 AB 中点, ⊙O是 的外接圆.
(1)求 BC的长;
(2)求⊙O的半径.
16.定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图1,在损矩形 ABCD 中,∠ABC=则该损矩形的直径是线段__________;
(2)在线段AC上确定一点 P,使损矩形的四个顶点都在以 P 为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由(友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹);
(3)如图2,在 中, 以AC为一边向三角形外作菱形ACEF,D为菱形 ACEF的中心,连接 BD,当 BD平分时,判断四边形ACEF 为何种特殊的四边形 请说明理由.若此时 求 BC的长.
参考答案
1. D 2. C 3. B 4. A 5. C 6. C 7. C
10. 30°
11.解:△ABE∽△ADC.
证明:∵AE是⊙O的直径,∴∠ABE=90°.
∵AD 是△ABC的边 BC 上的高,∴∠ADC=90°.∴∠ADC=∠ABE=90°.
又∵∠C=∠E,∴△ABE∽△ADC.
12.解:(1)证明:∵FA=FE,∴∠FAE=∠AEF.
∵∠FAE与∠BCE都是 所对的圆周角,∴∠FAE=∠BCE.
∵∠AEF=∠CEB,∴∠CEB=∠BCE.
∵CE平分∠ACD,∴∠ACE=∠DCE.
∵AB是直径,∴∠ACB=90°,∴∠CEB+∠DCE=∠BCE +∠ACE=∠ACB=90°,
∴∠CDE=90°,∴CD⊥AB;
(2)由(1)知,∠BEC=∠BCE,∴BE=BC.
∵AF=EF,FM⊥AB,∴MA=ME=2,AE=4.∴圆的半径(
在 中,
13.解:(1)证明:如图1所示,连接AO并延长, 交⊙O于点D,连接CD.
则
同理,
如图2所示,过点 C作 于点E.
14.解:(1)证明:如图,连接DC,则∠BDC=∠BAC=45°,
∵BD⊥BC,∴∠BCD=90°-∠BDC=45°,∴∠BCD=∠BDC,∴BD=BC;
(2)如图,∵∠DBC=90°,∴CD为⊙O的直径.∴CD=2r=6.
∵BF⊥AC,∴∠BMC=∠EBC=90°,
又∵∠BCM=∠BCE.∴△BCM∽△ECB,
连接CF,则∠F=∠BAC=45°,∠MCF=90°-45°=45°,
15.解:
D为AB 中点,
(2)过点 A 作 于点 E,连接CO并延长,交⊙O于点 F,连接AF,
∵在 中,
∴DE=1,
∵△BAC∽△BCD,
设CD=x,则
∵在Rt△ACE 中,
即 解得. (舍去),
∵∠AFC与 都是 所对的圆周角,∴∠AFC=∠ADC.
∵CF为⊙O的直径,
即⊙O的半径为
16.解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此 AC 是该损矩形的直径;故答案为:AC;
(2)作图如图1:
∵点 P 为AC 中点,
∴点A,B,C,D在以P 为圆心, 为半径的同一个圆上;
(3)∵四边形ACEF 为菱形,∴∠ADC=90°,AE=2AD,CF=2CD.
∴四边形 ABCD为损矩形.∴由(2)可知,点 A,B,C,D在同一个圆上.
∵BD平分∠ABC,∴∠ABD=∠CBD=45°.
∴AD=CD.∴AE=CF.∴四边形 ACEF为正方形.过点 D作DM⊥AB,DN⊥BC,如图2.
∵∠ABD=∠CBD=45°,BD=4 ,∴DM=BN=4,
S△BCD,
∴BC=5或BC=-3(舍去).∴BC=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
