人教B版选择性必修第二册 4.2.5 正态分布 课件(共30张PPT)
文档属性
| 名称 | 人教B版选择性必修第二册 4.2.5 正态分布 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 21:22:52 | ||
图片预览







文档简介
(共30张PPT)
正态分布
图上的钱币是德国的马克,钱币上的头像是德国有“数学王子”之称的高斯。和高斯头像一起出现在钱币上的,还有一段优美的曲线。如此重要的一条曲线是什么曲线呢?它是怎样得到的呢?这就是我们本节课需要探究的问题。
新课引入
问题1:自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量). 用随机变量X表示这种误差,则X是离散型随机变量吗?如果不是,请说明理由.
连续型随机变量:它们的取值充满某个区间甚至整个实轴,但是取某一点的概率为0
2、生活中还有哪些随机变量也是连续型随机变量
1、连续型随机变量和离散型随机变量有何区别
离散型随机变量的所有可能的取值都能一一列举;连续型随机变量可以在某个实数范围内连续取值。
某人在站台等车的时间X是连续型随机变量;某种无线电元件的寿命;某地区同龄人群的身高、体重、肺活量等都是连续型随机变量.
问题2:随机抽取了100袋食盐,获得误差X (单位: g) 的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1):如何描述这100个样本误差数据?
(1):如何描述这100个样本误差数据?
可研究误差X的最大值、最小值、均值、方差等。
也可以绘制频率分布直方图分析数据
(2):频率分布直方图的步骤如何?
第二步:确定组距和组数;
本问题中不妨令组距为2,将数据分为6组.
第一步:求极差;
极差指一组数据中的最大数据与最小数据的差.4.8-(-5.2)=10
第三步:确定区间分点,将数据分组:
[-6,-4),[-4,-2),[-2,0),[0,2),[2,4),[4,6]
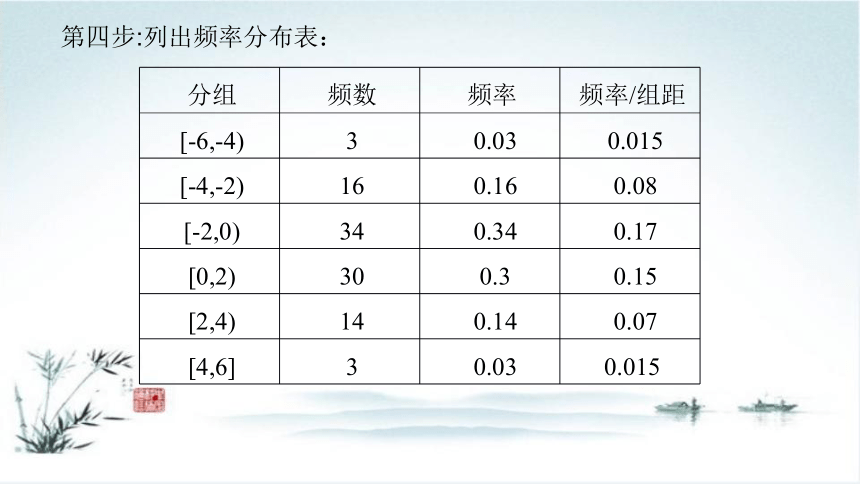
第四步:列出频率分布表:
分组 频数 频率 频率/组距
[-6,-4) 3 0.03 0.015
[-4,-2) 16 0.16 0.08
[-2,0) 34 0.34 0.17
[0,2) 30 0.3 0.15
[2,4) 14 0.14 0.07
[4,6] 3 0.03 0.015
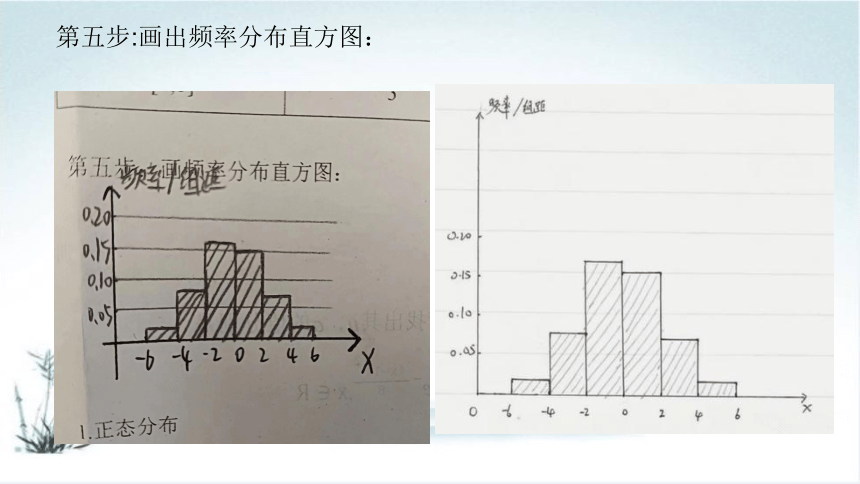
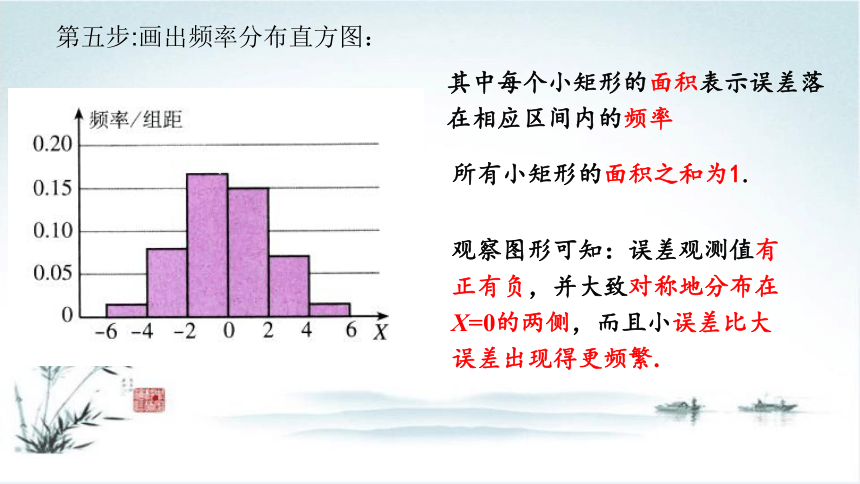
第五步:画出频率分布直方图:
观察图形可知:误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.
其中每个小矩形的面积表示误差落在相应区间内的频率
所有小矩形的面积之和为1.
第五步:画出频率分布直方图:
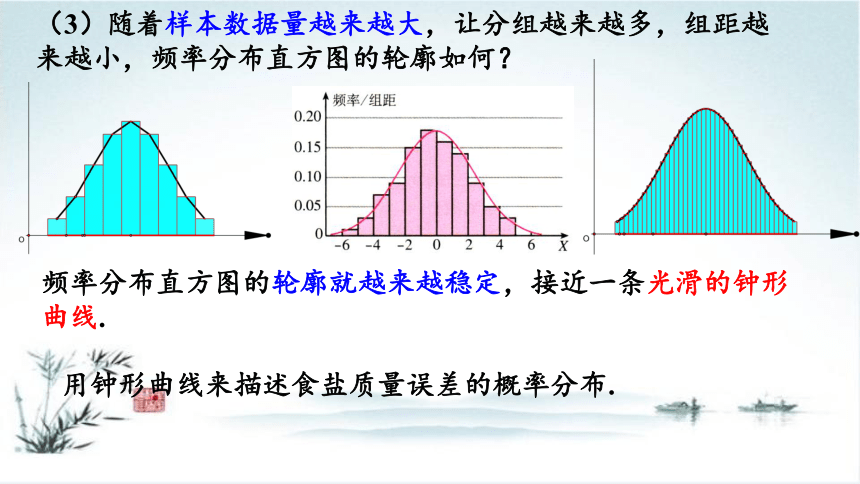
(3)随着样本数据量越来越大,让分组越来越多,组距越来越小,频率分布直方图的轮廓如何?
频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
用钟形曲线来描述食盐质量误差的概率分布.
面积即为概率!
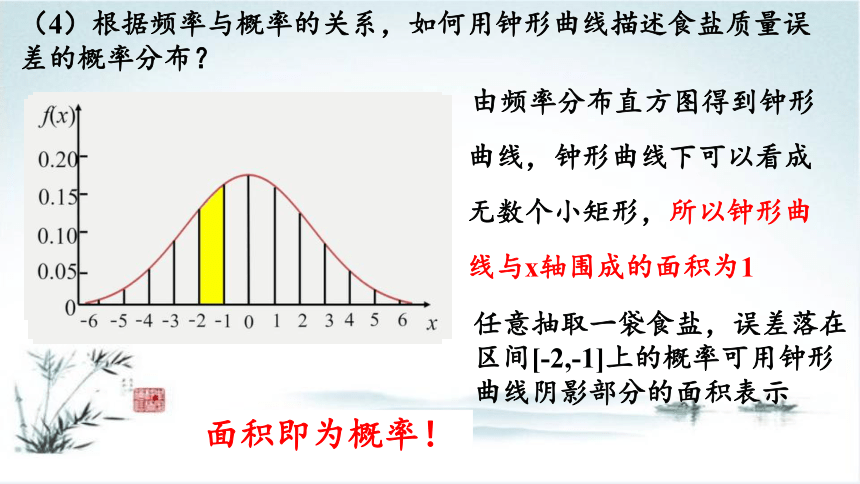
由频率分布直方图得到钟形曲线,钟形曲线下可以看成无数个小矩形,所以钟形曲线与x轴围成的面积为1
(4)根据频率与概率的关系,如何用钟形曲线描述食盐质量误差的概率分布?
任意抽取一袋食盐,误差落在区间[-2,-1]上的概率可用钟形曲线阴影部分的面积表示
问题3:图中的钟形曲线是一个函数图像吗?如果是,这个函数是否存在解析式?
其中μ∈R,σ>0为参数.
自然对数的底数e
圆周率
最小质数的算术平方根
我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线. 若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为X~N(μ, σ2).
特别地,当μ=0, σ=1时,称随机变量X服从标准正态分布.记为X~N(0, 1).
正态分布的定义
学习新知
求概率即求面积!
而P(a≤X≤b)为区域B的面积.
f (x)
x
μ
a
A
图 (4)
B
x
b
O
抽象概念,内涵辨析
若X~N(μ,σ2),则如右图所示,曲线与x轴围成的面积为
X取值不超过x的概率P(X≤x)为图中区域A的面积,
1
追问1:可以从哪些方面研究正态密度函数的性质?
定义域,值域,单调性,最值,奇偶性,对称性
追问2:观察正态曲线,你能发现正态曲线的哪些特点?
(1)曲线在x轴的上方,与x轴不相交.(非负性)
(2)曲线是单峰的,它关于直线x=μ对称.(对称性)
(3)曲线在x=μ处达到峰值 (最高点)
(4)当|x|无限增大时,曲线无限接近x轴(渐近线)
追问3:观察正态密度函数,证明正态曲线的特点?
(1)曲线在x轴的上方,与x轴不相交.(非负性)
(2)曲线是单峰的,它关于直线x=μ对称.(对称性)
(3)曲线在x=μ处达到峰值 (最高点)
(4)当|x|无限增大时,曲线无限接近x轴(渐近线)
追问3:观察正态密度函数,证明正态曲线的特点?
(4)当|x|无限增大时,
曲线无限接近x轴(渐近线)
(3)曲线在x=μ处
达到峰值(最高点)
0
1
2
-1
-2
x
y
-3
3
4
μ=1
0.5
1-a
a
1-a
1-2a
1.若X~N(1, σ2),且P(X<0)=a,则
(1) P(X>1)=_______;
(2) P(X>0)=______;
(3) P(X>2)=______;
(4) P(X<2)=______;
(5) P(0(6) P(00.5-a
快问快答,检验效果
问题4:一个正态分布由参数μ和 完全确定,这两个参数对正态曲线的形状有何影响?
当参数 固定时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移
问题4:一个正态分布由参数μ和 σ 完全确定,这两个参数对正态曲线的形状有何影响?
若X~N(μ, σ )则E(X) =μ、D(X)=σ .
μ反映了正态分布的集中位置,可以用均值来估计;
σ反映了随机变量的分布相对于均值μ的离散程度,可以用标准差来估计.
1. 若X~N(2, 32),则E(X)=______,D(X)=_______.
2
9
2. X~N(μ, σ2),若E(X)=3, D(X)=2,则μ=______, σ=_____.
3
快问快答,检验效果
在气象中,某地每年七月的平均气温、平均湿度、降雨量等…
正态分布在概率和统计中占有重要地位,广泛存在于自然界,生产及生活实践中,很多随机变量都服从或近似服从正态分布.
在生产中,在正常生产条件下各种产品的质量指标;
在生物学中,同一群体的某一特征(身高、体重等);
例1:给出下列两个正态分布的函数表达式,请找出其μ和σ
探究一、正态密度函数及其图像特点
训练1.已知三个正态分布密度函数
的图象如图所示,则下列结论正确的是( )
B
例2.在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少
(2).若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人
探究二、利用正态曲线求概率
训练2.若X~N(5,1),求P(61、正态密度曲线及正态密度函数
2、正态曲线的特点
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(3)曲线在x=μ处达到峰值
(4)当|x|无限增大时,曲线无限接近x轴
3、正态分布的3σ原则
正态分布的奇妙之处,就是许多看似随机的事件竟然服从一个表达式就能表达的分布,如同上帝之手特意为之.
--《创世纪数理统计·正态分布的前世今生》
正态分布
图上的钱币是德国的马克,钱币上的头像是德国有“数学王子”之称的高斯。和高斯头像一起出现在钱币上的,还有一段优美的曲线。如此重要的一条曲线是什么曲线呢?它是怎样得到的呢?这就是我们本节课需要探究的问题。
新课引入
问题1:自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量). 用随机变量X表示这种误差,则X是离散型随机变量吗?如果不是,请说明理由.
连续型随机变量:它们的取值充满某个区间甚至整个实轴,但是取某一点的概率为0
2、生活中还有哪些随机变量也是连续型随机变量
1、连续型随机变量和离散型随机变量有何区别
离散型随机变量的所有可能的取值都能一一列举;连续型随机变量可以在某个实数范围内连续取值。
某人在站台等车的时间X是连续型随机变量;某种无线电元件的寿命;某地区同龄人群的身高、体重、肺活量等都是连续型随机变量.
问题2:随机抽取了100袋食盐,获得误差X (单位: g) 的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1):如何描述这100个样本误差数据?
(1):如何描述这100个样本误差数据?
可研究误差X的最大值、最小值、均值、方差等。
也可以绘制频率分布直方图分析数据
(2):频率分布直方图的步骤如何?
第二步:确定组距和组数;
本问题中不妨令组距为2,将数据分为6组.
第一步:求极差;
极差指一组数据中的最大数据与最小数据的差.4.8-(-5.2)=10
第三步:确定区间分点,将数据分组:
[-6,-4),[-4,-2),[-2,0),[0,2),[2,4),[4,6]
第四步:列出频率分布表:
分组 频数 频率 频率/组距
[-6,-4) 3 0.03 0.015
[-4,-2) 16 0.16 0.08
[-2,0) 34 0.34 0.17
[0,2) 30 0.3 0.15
[2,4) 14 0.14 0.07
[4,6] 3 0.03 0.015
第五步:画出频率分布直方图:
观察图形可知:误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.
其中每个小矩形的面积表示误差落在相应区间内的频率
所有小矩形的面积之和为1.
第五步:画出频率分布直方图:
(3)随着样本数据量越来越大,让分组越来越多,组距越来越小,频率分布直方图的轮廓如何?
频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
用钟形曲线来描述食盐质量误差的概率分布.
面积即为概率!
由频率分布直方图得到钟形曲线,钟形曲线下可以看成无数个小矩形,所以钟形曲线与x轴围成的面积为1
(4)根据频率与概率的关系,如何用钟形曲线描述食盐质量误差的概率分布?
任意抽取一袋食盐,误差落在区间[-2,-1]上的概率可用钟形曲线阴影部分的面积表示
问题3:图中的钟形曲线是一个函数图像吗?如果是,这个函数是否存在解析式?
其中μ∈R,σ>0为参数.
自然对数的底数e
圆周率
最小质数的算术平方根
我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线. 若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为X~N(μ, σ2).
特别地,当μ=0, σ=1时,称随机变量X服从标准正态分布.记为X~N(0, 1).
正态分布的定义
学习新知
求概率即求面积!
而P(a≤X≤b)为区域B的面积.
f (x)
x
μ
a
A
图 (4)
B
x
b
O
抽象概念,内涵辨析
若X~N(μ,σ2),则如右图所示,曲线与x轴围成的面积为
X取值不超过x的概率P(X≤x)为图中区域A的面积,
1
追问1:可以从哪些方面研究正态密度函数的性质?
定义域,值域,单调性,最值,奇偶性,对称性
追问2:观察正态曲线,你能发现正态曲线的哪些特点?
(1)曲线在x轴的上方,与x轴不相交.(非负性)
(2)曲线是单峰的,它关于直线x=μ对称.(对称性)
(3)曲线在x=μ处达到峰值 (最高点)
(4)当|x|无限增大时,曲线无限接近x轴(渐近线)
追问3:观察正态密度函数,证明正态曲线的特点?
(1)曲线在x轴的上方,与x轴不相交.(非负性)
(2)曲线是单峰的,它关于直线x=μ对称.(对称性)
(3)曲线在x=μ处达到峰值 (最高点)
(4)当|x|无限增大时,曲线无限接近x轴(渐近线)
追问3:观察正态密度函数,证明正态曲线的特点?
(4)当|x|无限增大时,
曲线无限接近x轴(渐近线)
(3)曲线在x=μ处
达到峰值(最高点)
0
1
2
-1
-2
x
y
-3
3
4
μ=1
0.5
1-a
a
1-a
1-2a
1.若X~N(1, σ2),且P(X<0)=a,则
(1) P(X>1)=_______;
(2) P(X>0)=______;
(3) P(X>2)=______;
(4) P(X<2)=______;
(5) P(0
快问快答,检验效果
问题4:一个正态分布由参数μ和 完全确定,这两个参数对正态曲线的形状有何影响?
当参数 固定时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移
问题4:一个正态分布由参数μ和 σ 完全确定,这两个参数对正态曲线的形状有何影响?
若X~N(μ, σ )则E(X) =μ、D(X)=σ .
μ反映了正态分布的集中位置,可以用均值来估计;
σ反映了随机变量的分布相对于均值μ的离散程度,可以用标准差来估计.
1. 若X~N(2, 32),则E(X)=______,D(X)=_______.
2
9
2. X~N(μ, σ2),若E(X)=3, D(X)=2,则μ=______, σ=_____.
3
快问快答,检验效果
在气象中,某地每年七月的平均气温、平均湿度、降雨量等…
正态分布在概率和统计中占有重要地位,广泛存在于自然界,生产及生活实践中,很多随机变量都服从或近似服从正态分布.
在生产中,在正常生产条件下各种产品的质量指标;
在生物学中,同一群体的某一特征(身高、体重等);
例1:给出下列两个正态分布的函数表达式,请找出其μ和σ
探究一、正态密度函数及其图像特点
训练1.已知三个正态分布密度函数
的图象如图所示,则下列结论正确的是( )
B
例2.在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少
(2).若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人
探究二、利用正态曲线求概率
训练2.若X~N(5,1),求P(6
2、正态曲线的特点
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(3)曲线在x=μ处达到峰值
(4)当|x|无限增大时,曲线无限接近x轴
3、正态分布的3σ原则
正态分布的奇妙之处,就是许多看似随机的事件竟然服从一个表达式就能表达的分布,如同上帝之手特意为之.
--《创世纪数理统计·正态分布的前世今生》
