人教A版必修第一册 3.1.2 函数的解析式 课件(共19张PPT)
文档属性
| 名称 | 人教A版必修第一册 3.1.2 函数的解析式 课件(共19张PPT) | 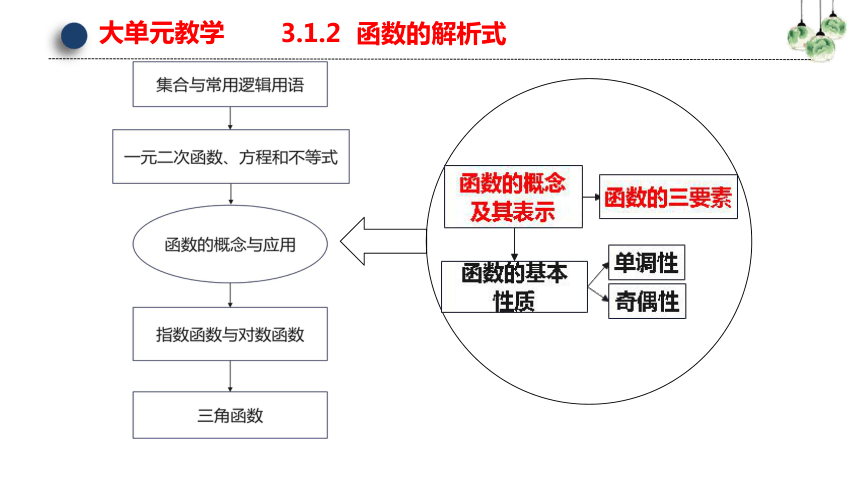 | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 21:23:30 | ||
图片预览






文档简介
(共19张PPT)
大单元教学
3.1.2 函数的解析式
复习回顾
1.函数三要素.
2.函数表示法.
定义域、值域、对应关系
列表法、图象法、解析法
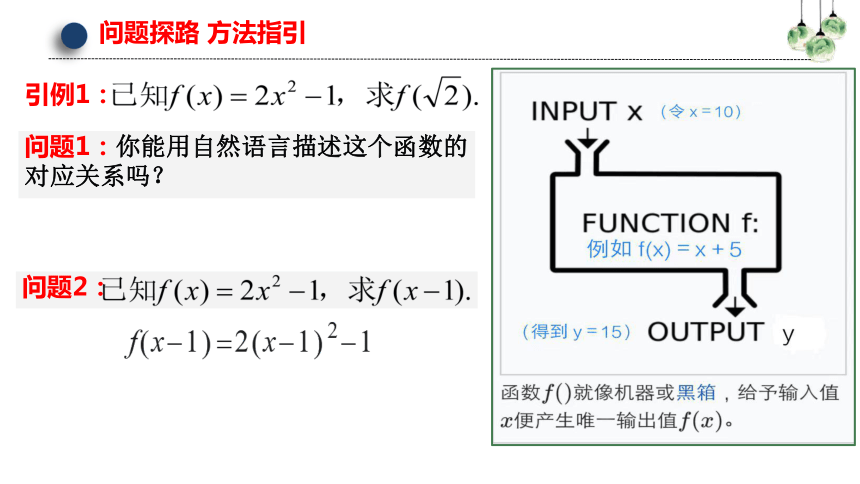
引例1:
问题1:你能用自然语言描述这个函数的对应关系吗?
问题2:
问题探路 方法指引
求函数的解析式——代入法
[方法小结]已知f (x)求f (g(x)),只需把f (x)中的x用g(x)代入即可.
例1
变式
问题3:用自然语言描述函数 的对应关系.
跟踪训练
A
问题探路 方法指引
引例2:
∵f(1)=1,f(-1)=-3,
设一次函数f(x)=kx+b(k≠0).
∴f(x)=2x-1.
解:
待定系数法
求函数的解析式——待定系数法
例2
[方法小结]已知函数模型(如:一次函数,二次函数等)求解析式,首先设出函数解析式,根据已知条件代入求系数.
跟踪训练
变式
问题探路 方法指引
引例3:
问题4:(1)请用自然语言描述这个函数的对应关系.
(2)
例1的
逆运算
求函数的解析式——配凑法
[方法小结] 配凑法是将解析式用括号内整体凑配出来,在解题时要注意“整体思想”的运用.
例3
跟踪训练
问题探路 方法指引
引例4:
例1
再究
问题5:
求函数的解析式——换元法
例4
例3
方法二
[方法小结] 对于形如y=f(g(x))的函数,求y=f(x)的解析式,通常用换元法,令t=g(x),从中求出(x=φ(t)),然后代入表达式,求出f(t)即得f(x)的表达式. 特别注意:换元法要注意新元的范围.
跟踪训练
问题探路 合作探究
(2)若 f(x)+2f(-x)=x2+2x,求f(x)的解析式.
(1)若 f(x)+2f(-x)=x2+2x,求 f(1).
引例5:
求函数的解析式——解方程组法
例5
解:
联立方程组
解得
[方法小结]已知关于f(x)与f(-x)的表达式或f(x)与f 的表达式,可根据已知条件再构造出另外一个等式构成方程组,通过解方程组求出f(x).
盘点收获 总结提升
“从特殊到一般,数学抽象,逻辑推理 ”
巩固练习 能力提升
挑战自我
研究性作业: 课本73页15-17
必做作业:(1)阅读课本75页
(2)课本72页4-14
目标检测
_____________.
___________.
大单元教学
3.1.2 函数的解析式
复习回顾
1.函数三要素.
2.函数表示法.
定义域、值域、对应关系
列表法、图象法、解析法
引例1:
问题1:你能用自然语言描述这个函数的对应关系吗?
问题2:
问题探路 方法指引
求函数的解析式——代入法
[方法小结]已知f (x)求f (g(x)),只需把f (x)中的x用g(x)代入即可.
例1
变式
问题3:用自然语言描述函数 的对应关系.
跟踪训练
A
问题探路 方法指引
引例2:
∵f(1)=1,f(-1)=-3,
设一次函数f(x)=kx+b(k≠0).
∴f(x)=2x-1.
解:
待定系数法
求函数的解析式——待定系数法
例2
[方法小结]已知函数模型(如:一次函数,二次函数等)求解析式,首先设出函数解析式,根据已知条件代入求系数.
跟踪训练
变式
问题探路 方法指引
引例3:
问题4:(1)请用自然语言描述这个函数的对应关系.
(2)
例1的
逆运算
求函数的解析式——配凑法
[方法小结] 配凑法是将解析式用括号内整体凑配出来,在解题时要注意“整体思想”的运用.
例3
跟踪训练
问题探路 方法指引
引例4:
例1
再究
问题5:
求函数的解析式——换元法
例4
例3
方法二
[方法小结] 对于形如y=f(g(x))的函数,求y=f(x)的解析式,通常用换元法,令t=g(x),从中求出(x=φ(t)),然后代入表达式,求出f(t)即得f(x)的表达式. 特别注意:换元法要注意新元的范围.
跟踪训练
问题探路 合作探究
(2)若 f(x)+2f(-x)=x2+2x,求f(x)的解析式.
(1)若 f(x)+2f(-x)=x2+2x,求 f(1).
引例5:
求函数的解析式——解方程组法
例5
解:
联立方程组
解得
[方法小结]已知关于f(x)与f(-x)的表达式或f(x)与f 的表达式,可根据已知条件再构造出另外一个等式构成方程组,通过解方程组求出f(x).
盘点收获 总结提升
“从特殊到一般,数学抽象,逻辑推理 ”
巩固练习 能力提升
挑战自我
研究性作业: 课本73页15-17
必做作业:(1)阅读课本75页
(2)课本72页4-14
目标检测
_____________.
___________.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
