人教A版 必修 第一册 5.2.1《三角函数的概念》 课件(共18张PPT)
文档属性
| 名称 | 人教A版 必修 第一册 5.2.1《三角函数的概念》 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
三角函数的概念
自然界的周期现象
函数是描述客观世界变化规律的重要模型
学习目标
1、掌握任意角的三角函数的定义
2、已知角α终边上一点,会求角α的各三角函数值
3、体会数学建模,数形结合,数学运算的基本核心素养
A
建立数学模型
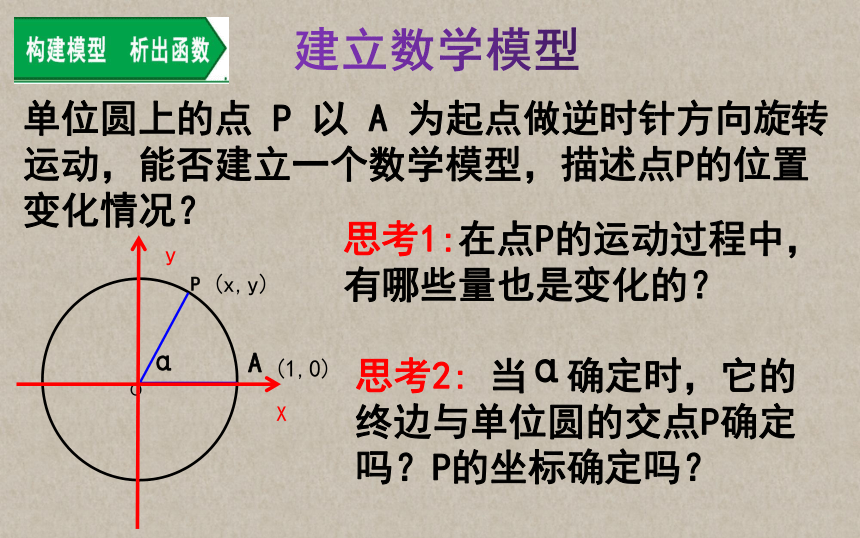
单位圆上的点 P 以 A 为起点做逆时针方向旋转运动,能否建立一个数学模型,描述点P的位置变化情况?
O
P
A
思考1: 在点P的运动过程中,有哪些量也是变化的?
建立数学模型
单位圆上的点 P 以 A 为起点做逆时针方向旋转运动,能否建立一个数学模型,描述点P的位置变化情况?
思考1:在点P的运动过程中,有哪些量也是变化的?
O
P
A
思考2: 当 确定时,它的终边与单位圆的交点P确定吗?P的坐标确定吗?
X
y
(1,0)
(x,y)
终边唯一确定
终边与单位圆的交点唯一
确定
思考3: 这种对应关系满足函数定义吗 若满足,自变量是谁?
终边唯一确定
P点横坐标X唯一确定
终边唯一确定
P点纵坐标y唯一确定
函数的定义:
设A、B是非空的实数集,如果对于A中的任意一个数X,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数。
终边唯一确定
终边与单位圆的交点唯一
确定
思考3: 这种对应关系满足函数定义吗 若满足,自变量是谁?
终边唯一确定
P点横坐标X唯一确定
终边唯一确定
P点纵坐标y唯一确定
三角函数的概念
正弦,余弦,正切函数都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
设α是任意角,α终边与单位圆交于点P(x,y)
(1)P的纵坐标y叫ɑ的正弦函数,记作sinɑ. 即
y= sinɑ
(2)P的横坐标x叫ɑ的余弦函数,记作cosɑ. 即 x= cosɑ
(3)P的纵坐标与横坐标的比值叫ɑ的正切函数,记作tanɑ.即 =tanɑ (x 0)
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数 y=sinX
余弦函数 y=cosX
正切函数 y=tanX
思考5:三个函数的定义域分别是什么
R
R
P
A
作者:湛江市第五中学钟景荣
例1:求 的正弦、余弦和正切值.
x
y
o
思考6:在本例中,角终边上任意找一点,三个三角函数值会发生改变吗?
14
分析:观察图5.2-5, 由▲OMP∽▲OM0P0,
例2: 如图5.2-4, 设α是一个任意角, 它的终边上任意一点P(不与原点O重合)的坐标为(x, y), 点P与原点的距离为r,
求证:sinα= , cosα= , tanα= .
根据三角函数的定义可证明.
O
图5.2-4
r=1
x
y
A(1,0)
P
P0
M
M0
作者:湛江市第五中学钟景荣
α
(5)
证明:如图5.2-5, 设角α的终边与单位圆
交于点P0(x0, y0). 分别过点P, P0作x轴的
垂线PM, P0M0,垂足分别为M, M0,
则| P0M0 |=| y0 |, | PM|=|y|,
则| OM0 |=| x0 |, | OM|=|x|,
▲OMP∽▲OM0P0,
∴,
即,
∵y0与y同号, ∴ y0,
即sinα= ,
同理可得 cosα= , tanα= .
(其中r=).
任意角α的三角函数值仅与 α 有关,而与点P 在角的终边上的位置无关.
单击此处
动画4超链接
15
设角α是一个任意角,P(x,y)是终边上的任意一点,点P与原点的距离r= >0.
那么① 叫做α的正弦,即sinα= ,
② 叫做α的余弦,即cosα= ,
③ 叫做α的正切,即tanα= (x ≠ 0).
概念推广:
O
P(x,y)
x
y
作者:湛江市第五中学钟景荣
α
16
作者:湛江市第五中学钟景荣
2. 已知角θ 的终边过点P(-12, 5), 求θ的三个三角函数值.
r = .
sinθ =
cosθ =
tanθ =
于是,
解:由已知可得:
= ,
= ,
= .
O
r
x
y
P(-12, 5)
M
θ
练习
课堂小结
1、本节课你收获了哪些新知识?
任意角三角函数的定义
会用两种方法求三角函数值
2、本节课用到了哪些数学思想?
数形结合、数学建模、由特殊到一般
1.利用三角函数定义,求 的三个三角函数值
2.已知角θ 的终边过点P(3,4 ), 求θ的三个三角函数值
18
课堂检测
三角函数的概念
自然界的周期现象
函数是描述客观世界变化规律的重要模型
学习目标
1、掌握任意角的三角函数的定义
2、已知角α终边上一点,会求角α的各三角函数值
3、体会数学建模,数形结合,数学运算的基本核心素养
A
建立数学模型
单位圆上的点 P 以 A 为起点做逆时针方向旋转运动,能否建立一个数学模型,描述点P的位置变化情况?
O
P
A
思考1: 在点P的运动过程中,有哪些量也是变化的?
建立数学模型
单位圆上的点 P 以 A 为起点做逆时针方向旋转运动,能否建立一个数学模型,描述点P的位置变化情况?
思考1:在点P的运动过程中,有哪些量也是变化的?
O
P
A
思考2: 当 确定时,它的终边与单位圆的交点P确定吗?P的坐标确定吗?
X
y
(1,0)
(x,y)
终边唯一确定
终边与单位圆的交点唯一
确定
思考3: 这种对应关系满足函数定义吗 若满足,自变量是谁?
终边唯一确定
P点横坐标X唯一确定
终边唯一确定
P点纵坐标y唯一确定
函数的定义:
设A、B是非空的实数集,如果对于A中的任意一个数X,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数。
终边唯一确定
终边与单位圆的交点唯一
确定
思考3: 这种对应关系满足函数定义吗 若满足,自变量是谁?
终边唯一确定
P点横坐标X唯一确定
终边唯一确定
P点纵坐标y唯一确定
三角函数的概念
正弦,余弦,正切函数都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
设α是任意角,α终边与单位圆交于点P(x,y)
(1)P的纵坐标y叫ɑ的正弦函数,记作sinɑ. 即
y= sinɑ
(2)P的横坐标x叫ɑ的余弦函数,记作cosɑ. 即 x= cosɑ
(3)P的纵坐标与横坐标的比值叫ɑ的正切函数,记作tanɑ.即 =tanɑ (x 0)
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数 y=sinX
余弦函数 y=cosX
正切函数 y=tanX
思考5:三个函数的定义域分别是什么
R
R
P
A
作者:湛江市第五中学钟景荣
例1:求 的正弦、余弦和正切值.
x
y
o
思考6:在本例中,角终边上任意找一点,三个三角函数值会发生改变吗?
14
分析:观察图5.2-5, 由▲OMP∽▲OM0P0,
例2: 如图5.2-4, 设α是一个任意角, 它的终边上任意一点P(不与原点O重合)的坐标为(x, y), 点P与原点的距离为r,
求证:sinα= , cosα= , tanα= .
根据三角函数的定义可证明.
O
图5.2-4
r=1
x
y
A(1,0)
P
P0
M
M0
作者:湛江市第五中学钟景荣
α
(5)
证明:如图5.2-5, 设角α的终边与单位圆
交于点P0(x0, y0). 分别过点P, P0作x轴的
垂线PM, P0M0,垂足分别为M, M0,
则| P0M0 |=| y0 |, | PM|=|y|,
则| OM0 |=| x0 |, | OM|=|x|,
▲OMP∽▲OM0P0,
∴,
即,
∵y0与y同号, ∴ y0,
即sinα= ,
同理可得 cosα= , tanα= .
(其中r=).
任意角α的三角函数值仅与 α 有关,而与点P 在角的终边上的位置无关.
单击此处
动画4超链接
15
设角α是一个任意角,P(x,y)是终边上的任意一点,点P与原点的距离r= >0.
那么① 叫做α的正弦,即sinα= ,
② 叫做α的余弦,即cosα= ,
③ 叫做α的正切,即tanα= (x ≠ 0).
概念推广:
O
P(x,y)
x
y
作者:湛江市第五中学钟景荣
α
16
作者:湛江市第五中学钟景荣
2. 已知角θ 的终边过点P(-12, 5), 求θ的三个三角函数值.
r = .
sinθ =
cosθ =
tanθ =
于是,
解:由已知可得:
= ,
= ,
= .
O
r
x
y
P(-12, 5)
M
θ
练习
课堂小结
1、本节课你收获了哪些新知识?
任意角三角函数的定义
会用两种方法求三角函数值
2、本节课用到了哪些数学思想?
数形结合、数学建模、由特殊到一般
1.利用三角函数定义,求 的三个三角函数值
2.已知角θ 的终边过点P(3,4 ), 求θ的三个三角函数值
18
课堂检测
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
