湖北省武汉市广雅中学2024-2025学年九年级上学期12月数学测试题(pdf版,无答案)
文档属性
| 名称 | 湖北省武汉市广雅中学2024-2025学年九年级上学期12月数学测试题(pdf版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-30 15:05:55 | ||
图片预览

文档简介
2024-2025
12
一、选择题(每小题3分,共30分)
1.下列环保标志,是中心对称图形的是()
2.一只不透明的袋子中装有5~个黑球和3个白球,这些球除颜色外无其它差别,从中任意
摸出4个球,下列事件是必然事件的为()
A.至少有1个球是白啡
B.至少有2个球是白球
C.至少有1个球是黑球
D,至少有2个球是黑球
3.一元二次方程2-4x-3=0配方后可化为()
A.(x-2)2=7B.(x-2)2=3C.(x+2)2=7D.(x+2)2=3
4.己知一元二次方程x一6x一4=0的两根分别为m,n,则m叶m+n的值是(
A.-10
B.-2
C.2
D.10
5.将二次函数=2x2向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为()
A.y=2(x+5i-3.B.y=2(x+5)2+3C,y=2(x-5)2-3D.v=2(x-5)2+3
6秋冬季是流感的高发时期,某校12月初有一人患了流感,经过两轮传染后,共49人患
流感,假设每轮传染中平均每人传染x人则可列方程()
A.1+x+2=49-B.x+x2=49C.1+x)2=49
D.x+x0+x)=49
7.从4张上面分别写着“元”“旦”“快”“乐”这4个字的卡片(大小、形状完全相同)
中随机抽取两张,则这两张卡片上面恰好写着“快”“乐”两个宇的概率是()
A
B.I
4
c
青
8.已知二次函数解析式为y=(x~3)2.4,当0A.0sy<5B.09.如图、AB是⊙O的直径,AC,BC是⊙O的弦,I是△ABC的内心,连接IO,B,IC,
若O1=2V2,∠B01=45°,则△B1C的面积Se的值为()
A,2W2+√5
,B.V2+2N5
C.2+25
D.2+2√2
D
第9题图
第10题图
0,如图,三次函数y=)-2与x轴交于A、B两点,与y轴交于C点,点D与点C
关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则
图中阴彩部分面积的最小值是()
A.16-82
B.8V2-8
C.3
D.24-12√2
二、英空题(每小题3分,共18分)
11.点P的坐标是(a,一2),点Q的坐标是(1,b),若PQ两点关于原点对称,则a+b=_
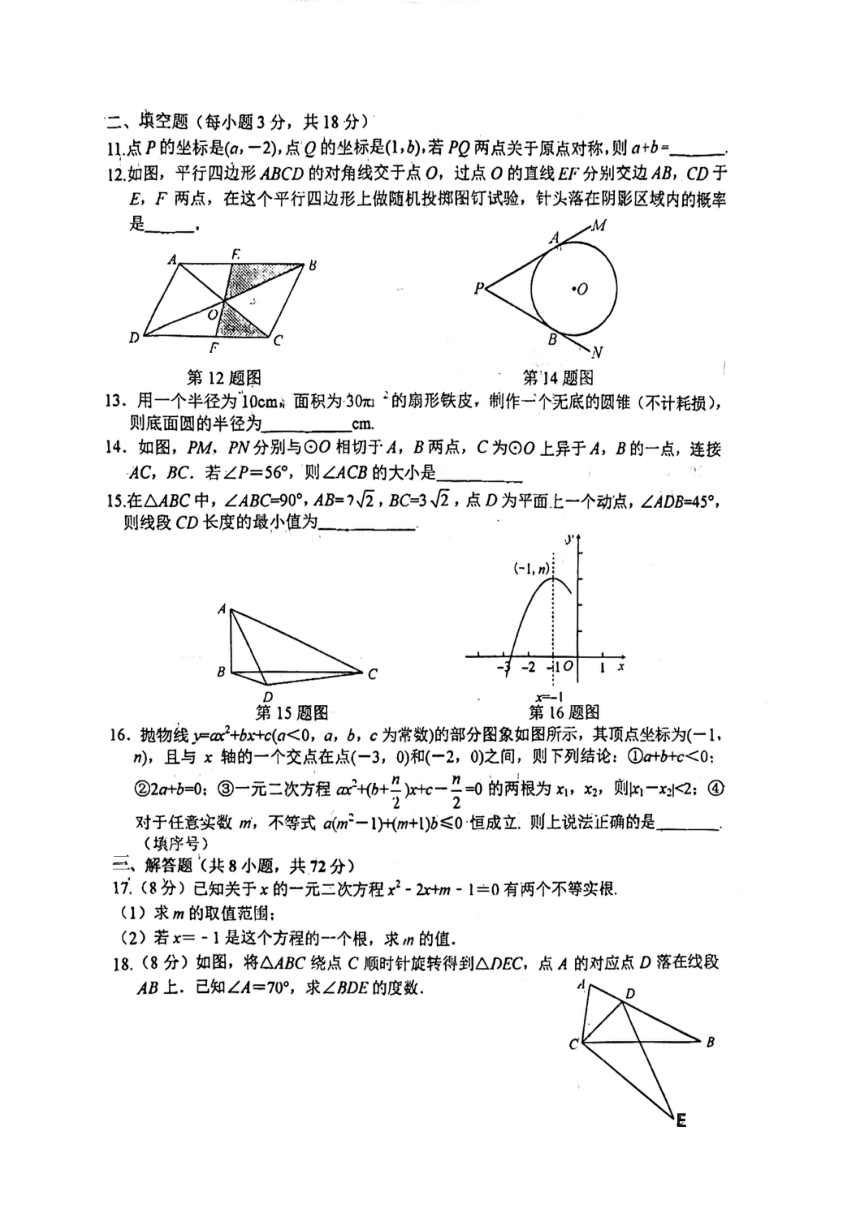
I2.如图,平行四边形ABCD的对角线交于点O,过点O的直线EF分别交边AB,CD于
E,F两点,在这个平行四边形上做随机投掷图钉试验,针头落在阴影区域内的概率
是
d
D
第12题图
第14题图
13.用一个半径为10cm面积为30元的扇形铁皮,制作一个无底的圆锥(不计耗损),
则底面圆的半径为
cm.
14.如图,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接
AC,BC.若∠P=56°,则∠ACB的大小是
15.在△ABC中,∠ABC=90°,AB=7V2,BC=3V2,点D为平面上一个动点,∠ADB=45°,
则线段CD长度的最小值为
(-I,n)i
B
--2101
D
1
第15题图
第16题图
16.抛物线y=2+b+c(a<0,a,b,c为常数)的部分图象如图所示,其顶点坐标为(一1,
n),且与x轴的一个交点在点(-3,0)和(一2,0)之间,则下列结论:①tb+c<0:
②2ab-0:国-元二次方程adb+号xe-号0的两根为,一2:@
对于任意实数m,不等式am-1Hm+1)b≤0恒成立.则上说法正确的是
(填序号)
-、解答题'(共8小题,共72分)
17.(8分)已知关于x的一无二次方程x2-2+m·1=0有两个不等实根
(1)求m的取值范围:
(2)若x=-1是这个方程的一个根,求n的值
18.(8分)如图,将△ABC绕点C顺时针旋转得到△DEC,点A的对应点D落在线段
AB上.已知∠A=70°,求∠BDE的度数.
12
一、选择题(每小题3分,共30分)
1.下列环保标志,是中心对称图形的是()
2.一只不透明的袋子中装有5~个黑球和3个白球,这些球除颜色外无其它差别,从中任意
摸出4个球,下列事件是必然事件的为()
A.至少有1个球是白啡
B.至少有2个球是白球
C.至少有1个球是黑球
D,至少有2个球是黑球
3.一元二次方程2-4x-3=0配方后可化为()
A.(x-2)2=7B.(x-2)2=3C.(x+2)2=7D.(x+2)2=3
4.己知一元二次方程x一6x一4=0的两根分别为m,n,则m叶m+n的值是(
A.-10
B.-2
C.2
D.10
5.将二次函数=2x2向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为()
A.y=2(x+5i-3.B.y=2(x+5)2+3C,y=2(x-5)2-3D.v=2(x-5)2+3
6秋冬季是流感的高发时期,某校12月初有一人患了流感,经过两轮传染后,共49人患
流感,假设每轮传染中平均每人传染x人则可列方程()
A.1+x+2=49-B.x+x2=49C.1+x)2=49
D.x+x0+x)=49
7.从4张上面分别写着“元”“旦”“快”“乐”这4个字的卡片(大小、形状完全相同)
中随机抽取两张,则这两张卡片上面恰好写着“快”“乐”两个宇的概率是()
A
B.I
4
c
青
8.已知二次函数解析式为y=(x~3)2.4,当0
若O1=2V2,∠B01=45°,则△B1C的面积Se的值为()
A,2W2+√5
,B.V2+2N5
C.2+25
D.2+2√2
D
第9题图
第10题图
0,如图,三次函数y=)-2与x轴交于A、B两点,与y轴交于C点,点D与点C
关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则
图中阴彩部分面积的最小值是()
A.16-82
B.8V2-8
C.3
D.24-12√2
二、英空题(每小题3分,共18分)
11.点P的坐标是(a,一2),点Q的坐标是(1,b),若PQ两点关于原点对称,则a+b=_
I2.如图,平行四边形ABCD的对角线交于点O,过点O的直线EF分别交边AB,CD于
E,F两点,在这个平行四边形上做随机投掷图钉试验,针头落在阴影区域内的概率
是
d
D
第12题图
第14题图
13.用一个半径为10cm面积为30元的扇形铁皮,制作一个无底的圆锥(不计耗损),
则底面圆的半径为
cm.
14.如图,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接
AC,BC.若∠P=56°,则∠ACB的大小是
15.在△ABC中,∠ABC=90°,AB=7V2,BC=3V2,点D为平面上一个动点,∠ADB=45°,
则线段CD长度的最小值为
(-I,n)i
B
--2101
D
1
第15题图
第16题图
16.抛物线y=2+b+c(a<0,a,b,c为常数)的部分图象如图所示,其顶点坐标为(一1,
n),且与x轴的一个交点在点(-3,0)和(一2,0)之间,则下列结论:①tb+c<0:
②2ab-0:国-元二次方程adb+号xe-号0的两根为,一2:@
对于任意实数m,不等式am-1Hm+1)b≤0恒成立.则上说法正确的是
(填序号)
-、解答题'(共8小题,共72分)
17.(8分)已知关于x的一无二次方程x2-2+m·1=0有两个不等实根
(1)求m的取值范围:
(2)若x=-1是这个方程的一个根,求n的值
18.(8分)如图,将△ABC绕点C顺时针旋转得到△DEC,点A的对应点D落在线段
AB上.已知∠A=70°,求∠BDE的度数.
同课章节目录
