人教A版 必修 第一册5.4.3 正切函数的性质与图象 课件(共14张PPT)
文档属性
| 名称 | 人教A版 必修 第一册5.4.3 正切函数的性质与图象 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 21:38:43 | ||
图片预览



文档简介
(共14张PPT)
温故知新
设 是一个任意角, ,它的终边 与单位圆相交于点 ,
把点 的纵坐标与横坐标的比值 叫做 的正切函数,记作 ,
即 .
1.正切函数的定义是什么?
通常记作:正切函数
2.正切函数的定义域是什么?
思路共研
问题1:根据研究正弦函数和余弦函数的经验,你认为应该如何研究正切函数的图象和性质?
问题2:你能用不同的方法研究正切函数吗?
作正切函数图象→根据图象研究性质
正切函数定义→性质→研究图象
(以数解形)
(以形助数)
数形结合
新知探究
诱导公式
诱导公式
奇函数
新知探究
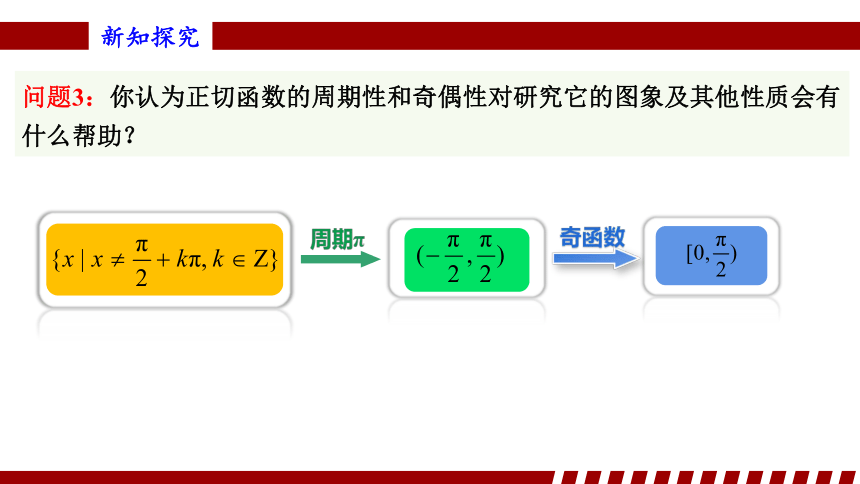
问题3:你认为正切函数的周期性和奇偶性对研究它的图象及其他性质会有什么帮助?
奇函数
周期π
新知探究
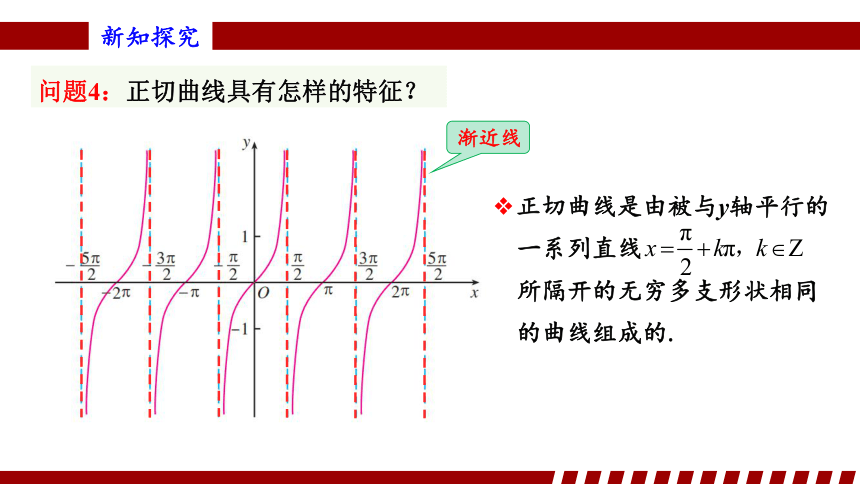
问题4:正切曲线具有怎样的特征?
正切曲线是由被与y轴平行的
一系列直线
所隔开的无穷多支形状相同
的曲线组成的.
渐近线
新知探究
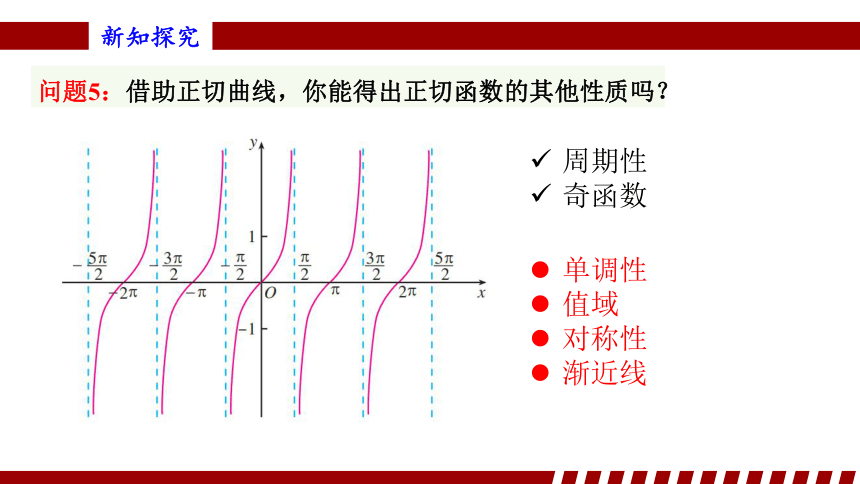
问题5:借助正切曲线,你能得出正切函数的其他性质吗?
周期性
奇函数
单调性
值域
对称性
渐近线
典例精析
【例1】求函数 的定义域、周期及单调区间.
1.求定义域体现了怎样的思想?你能不能用这个思想来求周期和单调区间?
思考:
整体代换的思想
2.你能归纳出 的周期公式?
3.你能总结下求函数 的单调区间的步骤吗?
学以致用
求函数 的定义域、周期及单调区间.
素养提升
认真观察课本上的图5.4-9,你能设计一个问题吗?
思考:
达标测评
总结升华
渐近线
对称性
解析式
y=tan x
图 象
定义域
值 域
R
奇偶性
奇函数
单调性
周期性
总结升华
数形结合 类比
整体代换 转化
一个图象
六条性质
四个思想
周期性 奇偶性
单调性 值 域
对称性 渐近线
正切曲线
分层作业
必做题:课本213页练习2题,习题5.4第7、9
选做题:课本习题5.4第13、14题
02
01
温故知新
设 是一个任意角, ,它的终边 与单位圆相交于点 ,
把点 的纵坐标与横坐标的比值 叫做 的正切函数,记作 ,
即 .
1.正切函数的定义是什么?
通常记作:正切函数
2.正切函数的定义域是什么?
思路共研
问题1:根据研究正弦函数和余弦函数的经验,你认为应该如何研究正切函数的图象和性质?
问题2:你能用不同的方法研究正切函数吗?
作正切函数图象→根据图象研究性质
正切函数定义→性质→研究图象
(以数解形)
(以形助数)
数形结合
新知探究
诱导公式
诱导公式
奇函数
新知探究
问题3:你认为正切函数的周期性和奇偶性对研究它的图象及其他性质会有什么帮助?
奇函数
周期π
新知探究
问题4:正切曲线具有怎样的特征?
正切曲线是由被与y轴平行的
一系列直线
所隔开的无穷多支形状相同
的曲线组成的.
渐近线
新知探究
问题5:借助正切曲线,你能得出正切函数的其他性质吗?
周期性
奇函数
单调性
值域
对称性
渐近线
典例精析
【例1】求函数 的定义域、周期及单调区间.
1.求定义域体现了怎样的思想?你能不能用这个思想来求周期和单调区间?
思考:
整体代换的思想
2.你能归纳出 的周期公式?
3.你能总结下求函数 的单调区间的步骤吗?
学以致用
求函数 的定义域、周期及单调区间.
素养提升
认真观察课本上的图5.4-9,你能设计一个问题吗?
思考:
达标测评
总结升华
渐近线
对称性
解析式
y=tan x
图 象
定义域
值 域
R
奇偶性
奇函数
单调性
周期性
总结升华
数形结合 类比
整体代换 转化
一个图象
六条性质
四个思想
周期性 奇偶性
单调性 值 域
对称性 渐近线
正切曲线
分层作业
必做题:课本213页练习2题,习题5.4第7、9
选做题:课本习题5.4第13、14题
02
01
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
