人教B版数学选择性必修第三册 5.1.1数列的概念 课件(共24张PPT)
文档属性
| 名称 | 人教B版数学选择性必修第三册 5.1.1数列的概念 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 894.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 21:44:36 | ||
图片预览








文档简介
(共24张PPT)
5.1.1数列的概念
意大利数学家 斐波那契
(1175年——1250年)
1,1,2,3,5,8,13,21,
…
学
习
目
标
1.通过日常生活和数学中的实例,能概括出数列的定义及有关概念;
2.能够根据数列的通项公式写出数列的任意一项,并能够根据数列的前几项归纳出其通项公式;
3.通过与函数概念的类比与对比,能总结出数列与函数的关系,并会判断数列的增减性。
探究一:数列的概念
(1)我国古代哲学著作《庄子》中有一句话:“一尺之捶,日取其半,万世不竭.”如果木棍初始长度为1,则每天截去一半之后木棍的长度分别为:
探究一:数列的概念
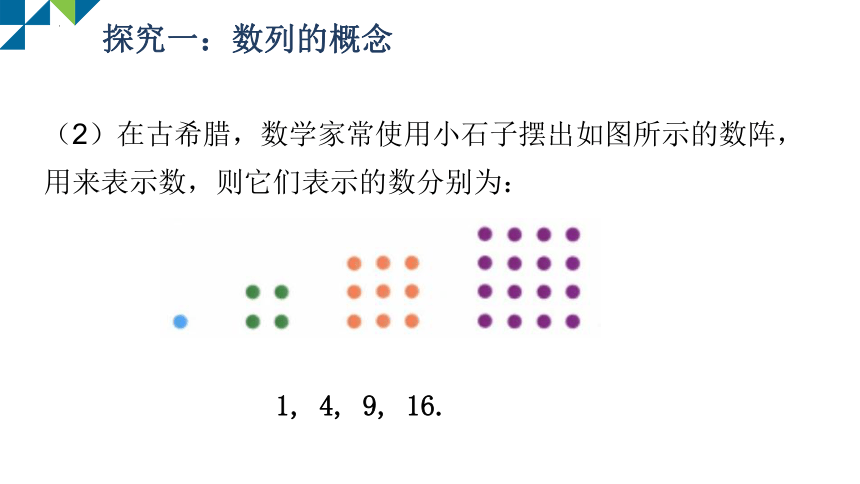
(2)在古希腊,数学家常使用小石子摆出如图所示的数阵,用来表示数,则它们表示的数分别为:
1, 4, 9, 16.
探究一:数列的概念
(3)从1984年至2016年,我国一共参加了9届夏季奥运会,按时间顺序所获得的金牌数分别为:
15, 5, 16, 16,28,32, 51, 38, 26.
1984年 1988年 1992年 1996年 2000年 2004年 2008年 2012年 2016年
15 5 16 16 28 32 51 38 26
探究一:数列的概念
(4)在“双11”活动中,标价为3000元的电脑,分别选择不分期、分3期、分6期、分12期、分24期不同分期付款方式,所对应的付款总金额分别为:
3000, 3045, 3090, 3180, 3600.
问题1:结合以上情境中的几列数,概括出数列的概念.
探究一:数列的概念
按一定次序排列的一列数称为数列.
探究一:数列的概念
数列:
问题4:数列与数集的区别是什么?
问题2:1,4,9,16与16,9,4,1是否为同一数列?
(1)数列中的数是按一定次序排列的,而数集中的元素是无序的.
(2)数列中的数可以重复,而数集中的数是不可重复的.
问题3:同一个数列,能否出现相同的数?
按一定次序排成的一列数称为数列.
探究一:数列的概念
数列:
数列的项:
数列中的每一个数都称为这个数列的项,
各项依次为这个数列的第1项(或首项),第2项…
数列的项数:
组成数列的数的个数称为数列的项数
数列的分类(项数的多少):
有穷数列
无穷数列
(项数有限的数列)
(项数无限的数列)
有穷数列:
无穷数列:
(2)(3)(4)
(1)
情
境
回
顾
下列各数列哪些是有穷数列,哪些是无穷数列
探究二:数列的通项
数列的一般形式:
正整数
称为数列的通项
探究二:数列的通项
为这个数列的一个通项公式.
数列的通项公式:
例1:根据下列数列的通项公式,写出对应数列的第2项和第5项.
【自主探究】根据通项公式写出数列中的项
检测1:
【合作探究】根据数列中的项写出数列的通项公式
检测2:
探究三:数列与函数的关系
思考1:与函数概念相类比,你构造出的数列中自变量、因变量、对应关系是什么?
自变量:
因变量:
对应关系:
探究三:数列与函数的关系
数列可以看成定义域为______________的函数,数列中的数就是自变量从小到大依次取_______时对应的函数值,而数列的_______也就是相应函数的解析式.
正整数集的子集
正整数
通项公式
数列是一种特殊的函数
思考2:数列与函数的关系是什么?
探究三:数列与函数的关系
数列的表示方法:通项公式、列表、图像
思考3:类比函数的表示方法,数列还可以如何表示?
思考4:类比函数的增减性,下列各数列哪些是递增数列,哪些是递减数列
递增数列
递减数列
探究三:数列与函数的关系
递增数列
探究三:数列与函数的关系
从第2项起,每一项都大于它的前一项的数列称为_____数列;
递增
递减
常数
常
递增数列
数列的分类(数列增减性):
递减数列
从第2项起,每一项都小于它的前一项的数列称为____数列;
各项都相等的数列称为____数列(简称为____数列).
合
作
探
究
例3:
按数列的增减性
课
堂
小
结
1
2
知识
思想方法
类比与对比
由特殊到一般
3
核心素养
由一般到特殊
数学抽象
逻辑推理
数学运算
5.1.1数列的概念
意大利数学家 斐波那契
(1175年——1250年)
1,1,2,3,5,8,13,21,
…
学
习
目
标
1.通过日常生活和数学中的实例,能概括出数列的定义及有关概念;
2.能够根据数列的通项公式写出数列的任意一项,并能够根据数列的前几项归纳出其通项公式;
3.通过与函数概念的类比与对比,能总结出数列与函数的关系,并会判断数列的增减性。
探究一:数列的概念
(1)我国古代哲学著作《庄子》中有一句话:“一尺之捶,日取其半,万世不竭.”如果木棍初始长度为1,则每天截去一半之后木棍的长度分别为:
探究一:数列的概念
(2)在古希腊,数学家常使用小石子摆出如图所示的数阵,用来表示数,则它们表示的数分别为:
1, 4, 9, 16.
探究一:数列的概念
(3)从1984年至2016年,我国一共参加了9届夏季奥运会,按时间顺序所获得的金牌数分别为:
15, 5, 16, 16,28,32, 51, 38, 26.
1984年 1988年 1992年 1996年 2000年 2004年 2008年 2012年 2016年
15 5 16 16 28 32 51 38 26
探究一:数列的概念
(4)在“双11”活动中,标价为3000元的电脑,分别选择不分期、分3期、分6期、分12期、分24期不同分期付款方式,所对应的付款总金额分别为:
3000, 3045, 3090, 3180, 3600.
问题1:结合以上情境中的几列数,概括出数列的概念.
探究一:数列的概念
按一定次序排列的一列数称为数列.
探究一:数列的概念
数列:
问题4:数列与数集的区别是什么?
问题2:1,4,9,16与16,9,4,1是否为同一数列?
(1)数列中的数是按一定次序排列的,而数集中的元素是无序的.
(2)数列中的数可以重复,而数集中的数是不可重复的.
问题3:同一个数列,能否出现相同的数?
按一定次序排成的一列数称为数列.
探究一:数列的概念
数列:
数列的项:
数列中的每一个数都称为这个数列的项,
各项依次为这个数列的第1项(或首项),第2项…
数列的项数:
组成数列的数的个数称为数列的项数
数列的分类(项数的多少):
有穷数列
无穷数列
(项数有限的数列)
(项数无限的数列)
有穷数列:
无穷数列:
(2)(3)(4)
(1)
情
境
回
顾
下列各数列哪些是有穷数列,哪些是无穷数列
探究二:数列的通项
数列的一般形式:
正整数
称为数列的通项
探究二:数列的通项
为这个数列的一个通项公式.
数列的通项公式:
例1:根据下列数列的通项公式,写出对应数列的第2项和第5项.
【自主探究】根据通项公式写出数列中的项
检测1:
【合作探究】根据数列中的项写出数列的通项公式
检测2:
探究三:数列与函数的关系
思考1:与函数概念相类比,你构造出的数列中自变量、因变量、对应关系是什么?
自变量:
因变量:
对应关系:
探究三:数列与函数的关系
数列可以看成定义域为______________的函数,数列中的数就是自变量从小到大依次取_______时对应的函数值,而数列的_______也就是相应函数的解析式.
正整数集的子集
正整数
通项公式
数列是一种特殊的函数
思考2:数列与函数的关系是什么?
探究三:数列与函数的关系
数列的表示方法:通项公式、列表、图像
思考3:类比函数的表示方法,数列还可以如何表示?
思考4:类比函数的增减性,下列各数列哪些是递增数列,哪些是递减数列
递增数列
递减数列
探究三:数列与函数的关系
递增数列
探究三:数列与函数的关系
从第2项起,每一项都大于它的前一项的数列称为_____数列;
递增
递减
常数
常
递增数列
数列的分类(数列增减性):
递减数列
从第2项起,每一项都小于它的前一项的数列称为____数列;
各项都相等的数列称为____数列(简称为____数列).
合
作
探
究
例3:
按数列的增减性
课
堂
小
结
1
2
知识
思想方法
类比与对比
由特殊到一般
3
核心素养
由一般到特殊
数学抽象
逻辑推理
数学运算
