2025年中考数学复习--由线段关系产生的函数关系问题 专题练习(含解析)
文档属性
| 名称 | 2025年中考数学复习--由线段关系产生的函数关系问题 专题练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 934.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
由线段关系产生的函数关系问题
1.一次函数y= kx+4与二次函数. 的图像的一个交点坐标为(1,2),另一个交点是该二次函数图像的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(02.如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE 折叠,顶点 D 恰好落在BC边上的点F 处,延长AE 交BC 的延长线于点G.
(1) 求线段CE 的长;
(2)如图2,点M、N 分别是线段AG、DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.
①写出y关于x的函数关系式,并求出y的最小值;
② 是否存在这样的点M,使△DMN 是等腰三角形 若存在,请求出x的值;若不存在,请说明理由.
3.如图1,在矩形ABCD 中,AD=4cm,AB=3cm, E为边BC上一点,BE=AB,连接AE.动点 P、Q从点A同时出发,点 P 以 cm/s的速度沿AE 向终点E运动;点Q以2cm/s的速度沿折线AD-DC向终点C运动.设点Q运动的时间为x(s),在运动过程中,点P、Q经过的路线与线段PQ围成的图形面积为y(cm ).
(1)AE= ,∠EAD= ;
(2)求y关于x的函数关系式,并写出自变量x的取值范围;
(3)当 时,直接写出x 的值.
4.如图1,梯形ABCD中,AD∥BC,AD=2,AB=BC=CD=6.动点 P 在射线BA上,以BP 为半径的⊙P 交边BC于点E(点E 与点C不重合),联结PE、PC,设BP=x, PC=y.
(1) 求证:PE ∥DC;
(2)求y关于x的函数解析式,并写出定义域;
(3)联结PD,当∠PDC=∠B时,以D为圆心半径为R的⊙D与⊙P 相交,求R 的取值范围;
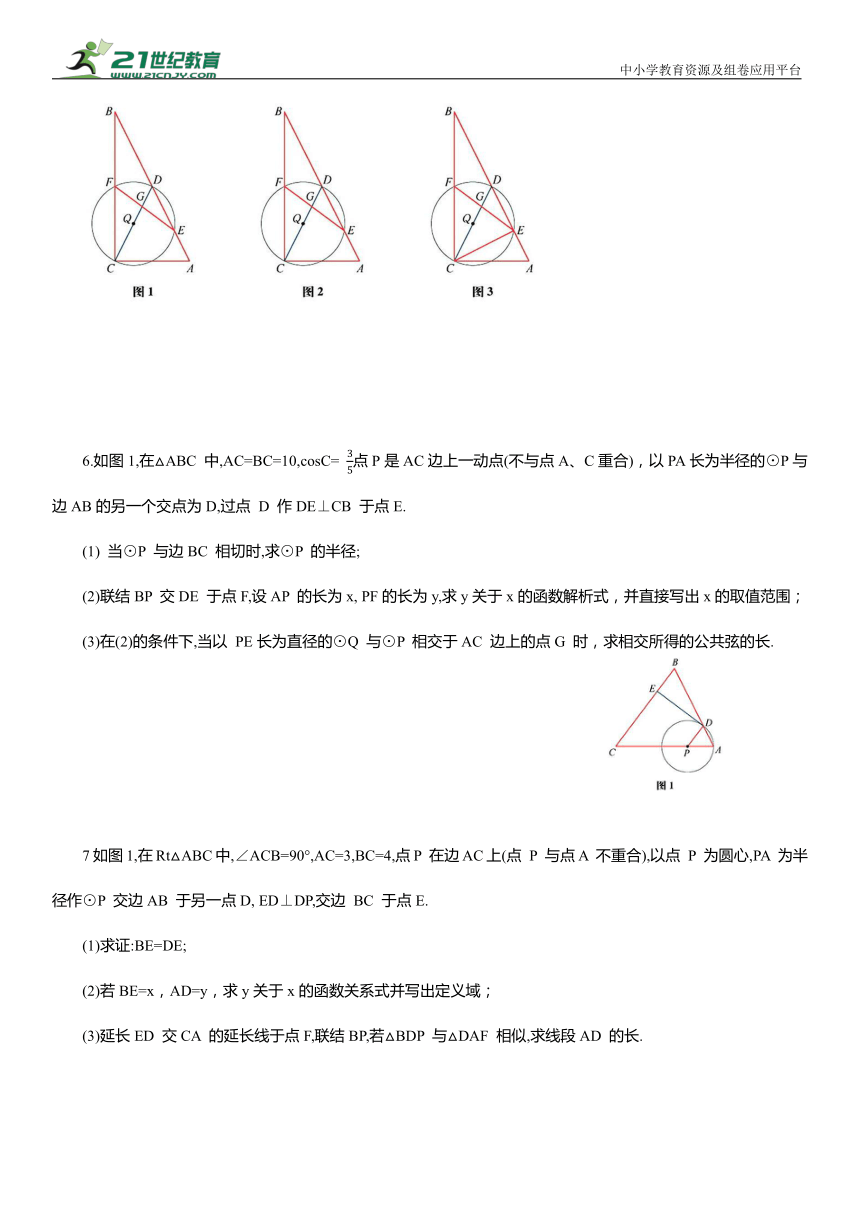
5.已知在Rt△ABC中,∠ACB=90°,AC=1, D是AB的中点.以CD为直径的⊙Q分别交BC、AB 于点F、E,点E 位于点D 下方,联结EF 交CD 于点G.
(1) 如图1,如果BC=2,求 DE 的长;
(2)如图2,设 求y关于x 的函数关系式及其定义域;
(3)如图3,联结CE,如果CG=CE,求BC的长.
6.如图1,在△ABC 中,AC=BC=10,cosC= 点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点 D 作DE⊥CB 于点E.
(1) 当⊙P 与边BC 相切时,求⊙P 的半径;
(2)联结BP 交DE 于点F,设AP 的长为x, PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围;
(3)在(2)的条件下,当以 PE长为直径的⊙Q 与⊙P 相交于AC 边上的点G 时,求相交所得的公共弦的长.
7如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P 在边AC上(点 P 与点A 不重合),以点 P 为圆心,PA 为半径作⊙P 交边AB 于另一点D, ED⊥DP,交边 BC 于点E.
(1)求证:BE=DE;
(2)若BE=x,AD=y,求y关于x的函数关系式并写出定义域;
(3)延长ED 交CA 的延长线于点F,联结BP,若△BDP 与△DAF 相似,求线段AD 的长.
8如图1,在平面直角坐标系中,四边形OABC 的顶点O 是坐标原点,点A 的坐标是(6, 0),点 B 的坐标是(0, 8),点 C 的坐标是 点M、N 分别为四边形OABC 边上的动点,动点M 从点O开始,以每秒1个单位长度的速度沿O-A-B路线向终点B 匀速运动,动点 N 从点O开始,以每秒2个单位长度的速度沿O-C-B-A 路线向终点A 匀速运动.点M、N同时从点O出发,当其中一点到达终点后,另一点也随之停止运动.设动点运动的时间为t秒(t>0),∠OMN 的面积为S.
(1) 填空:AB 的长度是 , BC 的长度是 ;
(2)当t=3时,求S的值;
(3)当3(4)若 请直接写出此时t的值.
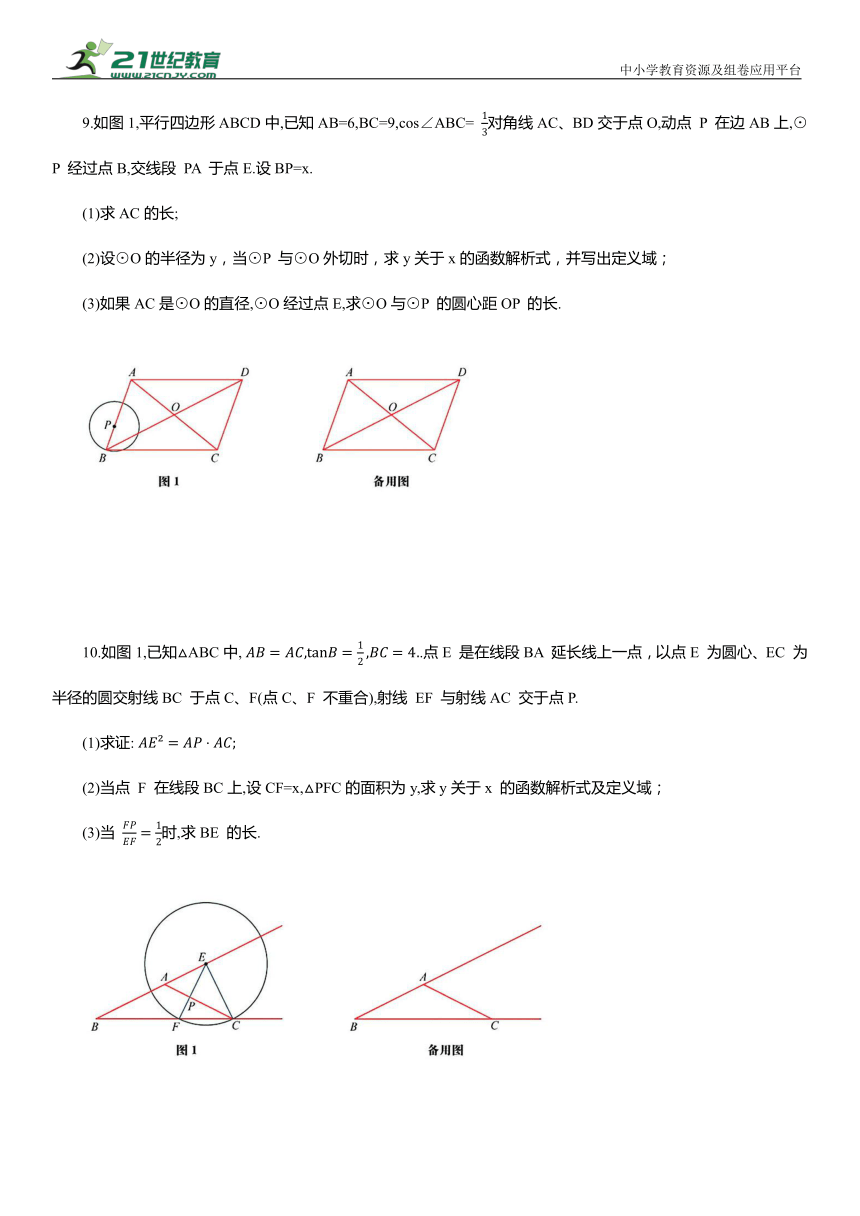
9.如图1,平行四边形ABCD中,已知AB=6,BC=9,cos∠ABC= 对角线AC、BD交于点O,动点 P 在边AB上,⊙P 经过点B,交线段 PA 于点E.设BP=x.
(1)求AC的长;
(2)设⊙O的半径为y,当⊙P 与⊙O外切时,求y关于x的函数解析式,并写出定义域;
(3)如果AC是⊙O的直径,⊙O经过点E,求⊙O与⊙P 的圆心距OP 的长.
10.如图1,已知△ABC中, .点E 是在线段BA 延长线上一点,以点E 为圆心、EC 为半径的圆交射线BC 于点C、F(点C、F 不重合),射线 EF 与射线AC 交于点P.
(1)求证:
(2)当点 F 在线段BC上,设CF=x,△PFC的面积为y,求y关于x 的函数解析式及定义域;
(3)当 时,求BE 的长.
1.满分解答
(1) 直线y= kx+4与y轴的交点为(0,4).
将点(1,2)代入y= kx+4,得2=k+4.解得k=-2.
抛物线 的对称轴为y轴,所以抛物线与直线y=-2x+4的交点(0,4)就是抛物线的顶点.所以
代入点(1,2),得2=a+4.解得a=-2.
所以
(2) 解方程 得
所以
所以 .
当m=1时,W取得最小值,最小值为7(如图1、图2所示).
考点伸展
深入讨论一下:抛物线 与y轴的交点不变,开口向下形状在改变,那么 取得最小值时,m的值与a 有怎样的关系
解方程 得 所以
所以
当 时,W取得最小值,最小值为
特别的,如果a=-2,当 时,
如果a=-1时,当 时, 如图3所示).
如果 时,当 时, 如图4所示).
我们再来看a为何值时,W的最小值可以取得最大值
由可知当 时,W的最小值可以取得最大值,最大值时16(如图4所示).
2.满分解答
(1)如图3,在Rt△ABF 中,AB=8,AF=10,所以BF=6.
在Rt△EFC中,FC=BC-BF=10-6=4,设CE=m,那么EF=ED=8-m.由勾股定理,得( 解得m=3.
(2)①第一步,计算说理DA=DG.
如图4,由AD ∥BG,得 所以 所以GC=6.
如图5,在Rt△DCG中,DC=8,GC=6,所以DG=10.
所以DA=DG.所以∠DAG=∠DGA.
在Rt△ABG中,AB=8, BG=16,所以.
第二步,证明△DAM∽△MGN.
由∠DMG=∠DAM+∠1,∠DMG=∠DMN+∠2,∠DAM=∠DMN,得∠1=∠2.
又因为∠DAM=∠MGN,所以△DAM∽△MGN.
所以 所以 所以
当 时,y取得最小值,最小值 此时M是AG 的中点,MN⊥DG.
②如图8所示,在等腰三角形DAG中,DA=DG=10, AG=8
已知∠DMN=∠A=∠G,分三种情况讨论等腰三角形DMN.
①如图8所示,如果DM=DN,那么∠DNM=∠DMN=∠G.
此时点 N 与点G 重合,不符合题意.
②如图9,当MD=MN时,由于△DAM∽△MGN,此时△DAM≌△MGN.
根据DA =MG,得 解得
③如图10,当 NM=ND时,∠NDM=∠DMN=∠G.此时△MDG∽△DAG.
所以 所以 解得
考点伸展
这道题目的情景图,把一个经典的长方形纸片翻折问题,稍微延伸了一下,又成为一个经典的几何计算说理问题,此时四边形AFGD 是菱形.这也是一个经典的“平分+平行,必有等腰三角形”的模型.
3.满分解答
(2)如图2,延长AE交DC 的延长线于点F,那么△ADF 是等腰直角三角形.因为AD=FD=4,所以.S△ADF =8.
①如图2,点Q在AD上时,0因为AQ=2x,所以
②如图3,点Q在DC上,点 P 未到达点E,2因为FQ=8-2x,所以
所以
③ 如图4,点Q 在DC 上,点 P 到达点E,
因为
所以
(3)当 时, 或
考点伸展
第(3)题的解题思路是这样的:
如图5,当点Q在AD上时,
所以 解得
如图6,当点 P 到达点E 的一瞬间,
所以在 范围内,存在
如图7,在 Rt△CEQ中, 所以
所以 解得
4.满分解答
(1) 如图2,因为PB=PE,所以∠B=∠PEB.
又因为∠B=∠C,所以∠PEB=∠C.
所以PE ∥DC.
(2) 如图3,作AF⊥BC于F, DG⊥BC 于G.
已知AD=2,BC=6,所以BF=FG=GC=2.
已知AB=DC=6,所以(
如图4,过点C作CH⊥AB 于H.
在Rt△BCH 中, 所以BH=2,CH=4
在Rt△CHP 中,
所以 定义域是0(3) 如图5,延长DP 交CB 的延长线于N,作NG⊥CD 于G.
因为∠PDC=∠B=∠C,所以ND=NC.所以GD=GC=3.
在 Rt△NCG中,因为 所以NC=9.所以ND=9, NB=3.
如图6,由AD∥BC,得
所以 解得
如图7,对于⊙D,rD=R;对于⊙P, 圆心距
因为两圆相交,所以
所以 解得
考点伸展
第(2)题求 PC 的长,也可以作 PQ⊥BC,解Rt△PBQ 和Rt△PCQ.如图8,在 Rt△PBQ中, 所以 在Rt△PCQ中,由勾股定理,得
5.满分解答
(1) 如图4,联结CE.因为CD为直径,所以∠CED=90°.
所以△ABC∽△ACE.
在Rt△ABC中,AC=1, BC=2,所以,
因为D 是AB 的中点,所以
由 得 解得
所以
(2) 如图5,联结FD、FQ.
因为CD 为直径,所以∠DFC=90°.所以FD∥CA.
所以 点 F 是BC 的中点.
所以 FQ 是△CDB 的中位线,
在Rt△ABC中,AC=1, BC=x,所以
由 得 解得
所以
由 定义域是x>1.
(3)如图6,因为EF 是Rt△BCE 斜边上的中线,所以FE=FB=FC.所以.
根据等角的余角相等,得∠1=∠A.
所以等腰三角形CEG∽等腰三角形DCA.
所以∠ECG=∠CDA.所以△CED 是等腰直角三角形.
设DE=CE=m,所以(
因为 所以 所以.
考点伸展
第(2)题中的定义域x>1的几何意义是什么呢 如图7,当点E、D重合时,斜边AB上的中线CD与高CE重合,所以CD垂直平分AB.此时△ABC是等腰直角三角形,x=CB=CA=1.当x>1时,点 E 在点D 的下方.
6.满分解答
(1) 如图2,做PH⊥BC于H.
当⊙P 与边BC 相切时, PH=PA=x.
在 Rt△CPH 中,cosC= ,PH=x, PC=CA-PA=10-x,
所以 即
解得 .所以⊙P 的半径为
(2)如图3,作BM⊥CA 于M.
在Rt△BCM中, 所以CM=6, BM=8.
在Rt△BAM中,AM=10-6=4, BM=8,所以tan∠A=2.
在 Rt△BMP 中,由勾股定理,得
如图4,作 PH⊥CB 于H.
因为CA=CB,PA=PD,所以∠A=∠ABC,∠A=∠1.
所以∠ABC=∠1.所以PD ∥CB.
于是可知四边形 PDEH 为矩形.所以HE=PD=x.
在 Rt△CPH 中,CP=CA PA=10 x,cosC= 所以
所以
由PD∥CB,得 所以
整理,得 定义域是0(3)如图5,因为∠EDP =90°,所以点D 也在以PE 为直径的⊙Q 上.
所以⊙Q 与⊙P 的公共弦为DG.因此 PE 垂直平分DG,∠2=∠3.
当点G落在AC边上时,EG⊥CA,∠GPD=∠2+∠3=∠A+∠1.
所以∠2=∠3=∠A=∠1.
在Rt△EGP中,PG=x,tan∠3=tan∠A=2,所以EG=2x.
在Rt△EGC中, 所以
由 解得
如图6,在 Rt△ADG中,已知
所以 所以
所以⊙Q 与⊙P 相交所得的公共弦的长为
考点伸展
第(3)题求 的过程,也可以不用推理∠2=∠3=∠A=∠1,根据EG=ED 列方程.
如图5,由PG=PD=PA,可知点D在以AG为直径的圆P上,所以∠GDA=90°.
又因为 PE垂直平分DG,所以PE ∥AB.
于是由CA=CB,可得CP=CE,AP=BE=x.
在 Rt△ECG中,CE=10-x, sin∠C= 所以
在Rt△BED中,BE=AP=x,tan∠B=2,所以ED=2x.
由EG=ED,得 解得
7满分解答
(1) 如图2,因为PA=PD,所以∠1=∠A.
已知ED⊥DP,根据等角的余角相等,得∠2=∠B.
所以BE=DE.
(2) 在 Rt△ABC中,AC=3, BC=4,所以.
如图2,作EM⊥AB 于M,所以BM=DM.
在Rt△BEM中, 所以
所以
所以
定义域为
(3)如图3,∠BDP 与△DAF 都是钝角三角形,那么以∠3为分类标准,分∠3=∠4和∠3=∠PBD 两种情况.
①先讨论∠3=∠4的情况.
第一步,求AF:AD 的值.
如图4,过点 F 向AB作垂线,垂足为N.
由于 可设FN=12m.
于是AF=15m,AN=9m,DN=16m.
所以AD=16m-9m=7m.所以
第二步,解△APD.作PH⊥AD 于H,那么
由 得 所以
第三步,根据对应边成比例列方程.
由 得 解得
②再讨论∠3=∠PBD 的情况.
如图5,由于∠3=∠2=∠CBA,所以点 P 与点C重合.
此时在等腰三角形ACD中,
考点伸展
图4中构造辅助线的策略,因为∠2=∠3=∠4=∠B,所以把∠3构造为直角三角形的锐角.也可以把∠4构造为直角三角形的锐角,过点B向PD作垂线.同样的方法,可得DB:DP=15:7.
如图4,在Rt△PDF 中,∠DPF 是定值,就是等腰三角形APD 的顶角.用面积法可以计算得到△PDF 的三边比时7:24:25.然后在 Rt△PBH 中,按照 PH:BH =7:24来列方程.
第(2)题的定义域为 这样思考:
当 P、C两点重合时,
解方程 得
当P、A两点重合时,. 解方程 得
8.满分解答
(1)AB=10,BC=6.
(2)如图2,当t=3时,点M 运动到OA 的中点,点 N 与点C重合.此时
(3)如图3,由B(0,8)、C(-2 ,4),可知点 C 在OB 的垂直平分线上.
设OB 的中点为D.作 NH⊥y轴于H.
在Rt△BCD中,BD=4,CD=2 ,所以
在Rt△BNH 中,BN=12-2t,所以
所以
(4)若 那么t 的值为8,
考点伸展
第(4)题要考虑三种情况:
①如图4,当点 N 在CB 上时,由 解得 舍去了负值).
② 当点M、N在AB 上时, 12,点O到AB 的距离为
(i) 如图5,点M、N 在相遇前,
由 解得t=8.
(ii) 如图6,点 M、N 在相遇后,MN=3t-28.
由 解得
9.满分解答
(1)如图2,作AF⊥BC于F.
在Rt△ABF 中, 所以BF=2.所以.
在Rt△ACF中,CF=BC-BF=9--2=7,所以,
(2)如图3,作CG⊥AB于G,作OH⊥AB 于H,那么(
在Rt△BCG中,. 所以BG=3.
所以CG=6 ,AG=3.所以(
如图4,在 Rt△OPH 中,
由勾股定理,得
整理,得
定义域是0(3)如图6,由 ,可知EO∥BC, E是AB 的中点.
由OH⊥AB,可知 H 是AE 的中点.
又因为 P 是BE 的中点,所以
在Rt△OPH 中, PH =3,OH =3 所以
如图7,特别地,当点 E 与点A 重合时,
考点伸展
第(1)题求 AC的长,用图3来解更便捷.
在Rt△BCG 中求得BG=3,可得CG 垂直平分AB,所以AC=BC=9.
10满分解答
(1) 如图2,由AB=AC,得∠1=∠2.
由EF=EC,得∠EFC=∠ECF.
所以∠EFC-∠1=∠ECF--∠2,即∠3=∠4.
又因为∠EAP=∠CAE,所以△AEP∽△ACE.
所以 所以
(2) 第一步,求△ECB 的面积.
如图3,作EH⊥BC于H,那么EH 垂直平分FC,所以
在Rt△EBH 中, 所以
所以
第二步,证明△PFC∽△ECB.
如图4,由∠2=∠1,∠EFC=∠ECF,得△PFC∽△ECB.
所以 所以
定义域是0(3)如图5,作AM⊥BC 于M,那么BM=CM=2.
在Rt△ABM中, 所以AM=1.
所以
① 如图6,当点 P 在BC 上时,如果 那么P是EF 的中点.
已知FE=CE,所以
由于△AEP∽△ACE,所以
所以 此时
② 如图7,当点 P 在BC 的延长线上时,如果 那么
同样的,△AEP ∽△ACE,所以
所以 此时
考点伸展
第(3)题也可以由△PFC∽△ECB 来解.
如图8所示,由 得BC=2CF=2x.
过点 E 作BC 的平行线交CA 的延长线于N.
①如图8,当点 P 在BC 上时,如果 那么 P 是EF 的中点.
所以NE=CF=x.
由 得 所以
②如图9,当点 P 在BC 的延长线上时,如果 那么 所以
由 得 所以
由线段关系产生的函数关系问题
1.一次函数y= kx+4与二次函数. 的图像的一个交点坐标为(1,2),另一个交点是该二次函数图像的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0
(1) 求线段CE 的长;
(2)如图2,点M、N 分别是线段AG、DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.
①写出y关于x的函数关系式,并求出y的最小值;
② 是否存在这样的点M,使△DMN 是等腰三角形 若存在,请求出x的值;若不存在,请说明理由.
3.如图1,在矩形ABCD 中,AD=4cm,AB=3cm, E为边BC上一点,BE=AB,连接AE.动点 P、Q从点A同时出发,点 P 以 cm/s的速度沿AE 向终点E运动;点Q以2cm/s的速度沿折线AD-DC向终点C运动.设点Q运动的时间为x(s),在运动过程中,点P、Q经过的路线与线段PQ围成的图形面积为y(cm ).
(1)AE= ,∠EAD= ;
(2)求y关于x的函数关系式,并写出自变量x的取值范围;
(3)当 时,直接写出x 的值.
4.如图1,梯形ABCD中,AD∥BC,AD=2,AB=BC=CD=6.动点 P 在射线BA上,以BP 为半径的⊙P 交边BC于点E(点E 与点C不重合),联结PE、PC,设BP=x, PC=y.
(1) 求证:PE ∥DC;
(2)求y关于x的函数解析式,并写出定义域;
(3)联结PD,当∠PDC=∠B时,以D为圆心半径为R的⊙D与⊙P 相交,求R 的取值范围;
5.已知在Rt△ABC中,∠ACB=90°,AC=1, D是AB的中点.以CD为直径的⊙Q分别交BC、AB 于点F、E,点E 位于点D 下方,联结EF 交CD 于点G.
(1) 如图1,如果BC=2,求 DE 的长;
(2)如图2,设 求y关于x 的函数关系式及其定义域;
(3)如图3,联结CE,如果CG=CE,求BC的长.
6.如图1,在△ABC 中,AC=BC=10,cosC= 点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点 D 作DE⊥CB 于点E.
(1) 当⊙P 与边BC 相切时,求⊙P 的半径;
(2)联结BP 交DE 于点F,设AP 的长为x, PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围;
(3)在(2)的条件下,当以 PE长为直径的⊙Q 与⊙P 相交于AC 边上的点G 时,求相交所得的公共弦的长.
7如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P 在边AC上(点 P 与点A 不重合),以点 P 为圆心,PA 为半径作⊙P 交边AB 于另一点D, ED⊥DP,交边 BC 于点E.
(1)求证:BE=DE;
(2)若BE=x,AD=y,求y关于x的函数关系式并写出定义域;
(3)延长ED 交CA 的延长线于点F,联结BP,若△BDP 与△DAF 相似,求线段AD 的长.
8如图1,在平面直角坐标系中,四边形OABC 的顶点O 是坐标原点,点A 的坐标是(6, 0),点 B 的坐标是(0, 8),点 C 的坐标是 点M、N 分别为四边形OABC 边上的动点,动点M 从点O开始,以每秒1个单位长度的速度沿O-A-B路线向终点B 匀速运动,动点 N 从点O开始,以每秒2个单位长度的速度沿O-C-B-A 路线向终点A 匀速运动.点M、N同时从点O出发,当其中一点到达终点后,另一点也随之停止运动.设动点运动的时间为t秒(t>0),∠OMN 的面积为S.
(1) 填空:AB 的长度是 , BC 的长度是 ;
(2)当t=3时,求S的值;
(3)当3
9.如图1,平行四边形ABCD中,已知AB=6,BC=9,cos∠ABC= 对角线AC、BD交于点O,动点 P 在边AB上,⊙P 经过点B,交线段 PA 于点E.设BP=x.
(1)求AC的长;
(2)设⊙O的半径为y,当⊙P 与⊙O外切时,求y关于x的函数解析式,并写出定义域;
(3)如果AC是⊙O的直径,⊙O经过点E,求⊙O与⊙P 的圆心距OP 的长.
10.如图1,已知△ABC中, .点E 是在线段BA 延长线上一点,以点E 为圆心、EC 为半径的圆交射线BC 于点C、F(点C、F 不重合),射线 EF 与射线AC 交于点P.
(1)求证:
(2)当点 F 在线段BC上,设CF=x,△PFC的面积为y,求y关于x 的函数解析式及定义域;
(3)当 时,求BE 的长.
1.满分解答
(1) 直线y= kx+4与y轴的交点为(0,4).
将点(1,2)代入y= kx+4,得2=k+4.解得k=-2.
抛物线 的对称轴为y轴,所以抛物线与直线y=-2x+4的交点(0,4)就是抛物线的顶点.所以
代入点(1,2),得2=a+4.解得a=-2.
所以
(2) 解方程 得
所以
所以 .
当m=1时,W取得最小值,最小值为7(如图1、图2所示).
考点伸展
深入讨论一下:抛物线 与y轴的交点不变,开口向下形状在改变,那么 取得最小值时,m的值与a 有怎样的关系
解方程 得 所以
所以
当 时,W取得最小值,最小值为
特别的,如果a=-2,当 时,
如果a=-1时,当 时, 如图3所示).
如果 时,当 时, 如图4所示).
我们再来看a为何值时,W的最小值可以取得最大值
由可知当 时,W的最小值可以取得最大值,最大值时16(如图4所示).
2.满分解答
(1)如图3,在Rt△ABF 中,AB=8,AF=10,所以BF=6.
在Rt△EFC中,FC=BC-BF=10-6=4,设CE=m,那么EF=ED=8-m.由勾股定理,得( 解得m=3.
(2)①第一步,计算说理DA=DG.
如图4,由AD ∥BG,得 所以 所以GC=6.
如图5,在Rt△DCG中,DC=8,GC=6,所以DG=10.
所以DA=DG.所以∠DAG=∠DGA.
在Rt△ABG中,AB=8, BG=16,所以.
第二步,证明△DAM∽△MGN.
由∠DMG=∠DAM+∠1,∠DMG=∠DMN+∠2,∠DAM=∠DMN,得∠1=∠2.
又因为∠DAM=∠MGN,所以△DAM∽△MGN.
所以 所以 所以
当 时,y取得最小值,最小值 此时M是AG 的中点,MN⊥DG.
②如图8所示,在等腰三角形DAG中,DA=DG=10, AG=8
已知∠DMN=∠A=∠G,分三种情况讨论等腰三角形DMN.
①如图8所示,如果DM=DN,那么∠DNM=∠DMN=∠G.
此时点 N 与点G 重合,不符合题意.
②如图9,当MD=MN时,由于△DAM∽△MGN,此时△DAM≌△MGN.
根据DA =MG,得 解得
③如图10,当 NM=ND时,∠NDM=∠DMN=∠G.此时△MDG∽△DAG.
所以 所以 解得
考点伸展
这道题目的情景图,把一个经典的长方形纸片翻折问题,稍微延伸了一下,又成为一个经典的几何计算说理问题,此时四边形AFGD 是菱形.这也是一个经典的“平分+平行,必有等腰三角形”的模型.
3.满分解答
(2)如图2,延长AE交DC 的延长线于点F,那么△ADF 是等腰直角三角形.因为AD=FD=4,所以.S△ADF =8.
①如图2,点Q在AD上时,0
②如图3,点Q在DC上,点 P 未到达点E,2
所以
③ 如图4,点Q 在DC 上,点 P 到达点E,
因为
所以
(3)当 时, 或
考点伸展
第(3)题的解题思路是这样的:
如图5,当点Q在AD上时,
所以 解得
如图6,当点 P 到达点E 的一瞬间,
所以在 范围内,存在
如图7,在 Rt△CEQ中, 所以
所以 解得
4.满分解答
(1) 如图2,因为PB=PE,所以∠B=∠PEB.
又因为∠B=∠C,所以∠PEB=∠C.
所以PE ∥DC.
(2) 如图3,作AF⊥BC于F, DG⊥BC 于G.
已知AD=2,BC=6,所以BF=FG=GC=2.
已知AB=DC=6,所以(
如图4,过点C作CH⊥AB 于H.
在Rt△BCH 中, 所以BH=2,CH=4
在Rt△CHP 中,
所以 定义域是0
因为∠PDC=∠B=∠C,所以ND=NC.所以GD=GC=3.
在 Rt△NCG中,因为 所以NC=9.所以ND=9, NB=3.
如图6,由AD∥BC,得
所以 解得
如图7,对于⊙D,rD=R;对于⊙P, 圆心距
因为两圆相交,所以
所以 解得
考点伸展
第(2)题求 PC 的长,也可以作 PQ⊥BC,解Rt△PBQ 和Rt△PCQ.如图8,在 Rt△PBQ中, 所以 在Rt△PCQ中,由勾股定理,得
5.满分解答
(1) 如图4,联结CE.因为CD为直径,所以∠CED=90°.
所以△ABC∽△ACE.
在Rt△ABC中,AC=1, BC=2,所以,
因为D 是AB 的中点,所以
由 得 解得
所以
(2) 如图5,联结FD、FQ.
因为CD 为直径,所以∠DFC=90°.所以FD∥CA.
所以 点 F 是BC 的中点.
所以 FQ 是△CDB 的中位线,
在Rt△ABC中,AC=1, BC=x,所以
由 得 解得
所以
由 定义域是x>1.
(3)如图6,因为EF 是Rt△BCE 斜边上的中线,所以FE=FB=FC.所以.
根据等角的余角相等,得∠1=∠A.
所以等腰三角形CEG∽等腰三角形DCA.
所以∠ECG=∠CDA.所以△CED 是等腰直角三角形.
设DE=CE=m,所以(
因为 所以 所以.
考点伸展
第(2)题中的定义域x>1的几何意义是什么呢 如图7,当点E、D重合时,斜边AB上的中线CD与高CE重合,所以CD垂直平分AB.此时△ABC是等腰直角三角形,x=CB=CA=1.当x>1时,点 E 在点D 的下方.
6.满分解答
(1) 如图2,做PH⊥BC于H.
当⊙P 与边BC 相切时, PH=PA=x.
在 Rt△CPH 中,cosC= ,PH=x, PC=CA-PA=10-x,
所以 即
解得 .所以⊙P 的半径为
(2)如图3,作BM⊥CA 于M.
在Rt△BCM中, 所以CM=6, BM=8.
在Rt△BAM中,AM=10-6=4, BM=8,所以tan∠A=2.
在 Rt△BMP 中,由勾股定理,得
如图4,作 PH⊥CB 于H.
因为CA=CB,PA=PD,所以∠A=∠ABC,∠A=∠1.
所以∠ABC=∠1.所以PD ∥CB.
于是可知四边形 PDEH 为矩形.所以HE=PD=x.
在 Rt△CPH 中,CP=CA PA=10 x,cosC= 所以
所以
由PD∥CB,得 所以
整理,得 定义域是0
所以⊙Q 与⊙P 的公共弦为DG.因此 PE 垂直平分DG,∠2=∠3.
当点G落在AC边上时,EG⊥CA,∠GPD=∠2+∠3=∠A+∠1.
所以∠2=∠3=∠A=∠1.
在Rt△EGP中,PG=x,tan∠3=tan∠A=2,所以EG=2x.
在Rt△EGC中, 所以
由 解得
如图6,在 Rt△ADG中,已知
所以 所以
所以⊙Q 与⊙P 相交所得的公共弦的长为
考点伸展
第(3)题求 的过程,也可以不用推理∠2=∠3=∠A=∠1,根据EG=ED 列方程.
如图5,由PG=PD=PA,可知点D在以AG为直径的圆P上,所以∠GDA=90°.
又因为 PE垂直平分DG,所以PE ∥AB.
于是由CA=CB,可得CP=CE,AP=BE=x.
在 Rt△ECG中,CE=10-x, sin∠C= 所以
在Rt△BED中,BE=AP=x,tan∠B=2,所以ED=2x.
由EG=ED,得 解得
7满分解答
(1) 如图2,因为PA=PD,所以∠1=∠A.
已知ED⊥DP,根据等角的余角相等,得∠2=∠B.
所以BE=DE.
(2) 在 Rt△ABC中,AC=3, BC=4,所以.
如图2,作EM⊥AB 于M,所以BM=DM.
在Rt△BEM中, 所以
所以
所以
定义域为
(3)如图3,∠BDP 与△DAF 都是钝角三角形,那么以∠3为分类标准,分∠3=∠4和∠3=∠PBD 两种情况.
①先讨论∠3=∠4的情况.
第一步,求AF:AD 的值.
如图4,过点 F 向AB作垂线,垂足为N.
由于 可设FN=12m.
于是AF=15m,AN=9m,DN=16m.
所以AD=16m-9m=7m.所以
第二步,解△APD.作PH⊥AD 于H,那么
由 得 所以
第三步,根据对应边成比例列方程.
由 得 解得
②再讨论∠3=∠PBD 的情况.
如图5,由于∠3=∠2=∠CBA,所以点 P 与点C重合.
此时在等腰三角形ACD中,
考点伸展
图4中构造辅助线的策略,因为∠2=∠3=∠4=∠B,所以把∠3构造为直角三角形的锐角.也可以把∠4构造为直角三角形的锐角,过点B向PD作垂线.同样的方法,可得DB:DP=15:7.
如图4,在Rt△PDF 中,∠DPF 是定值,就是等腰三角形APD 的顶角.用面积法可以计算得到△PDF 的三边比时7:24:25.然后在 Rt△PBH 中,按照 PH:BH =7:24来列方程.
第(2)题的定义域为 这样思考:
当 P、C两点重合时,
解方程 得
当P、A两点重合时,. 解方程 得
8.满分解答
(1)AB=10,BC=6.
(2)如图2,当t=3时,点M 运动到OA 的中点,点 N 与点C重合.此时
(3)如图3,由B(0,8)、C(-2 ,4),可知点 C 在OB 的垂直平分线上.
设OB 的中点为D.作 NH⊥y轴于H.
在Rt△BCD中,BD=4,CD=2 ,所以
在Rt△BNH 中,BN=12-2t,所以
所以
(4)若 那么t 的值为8,
考点伸展
第(4)题要考虑三种情况:
①如图4,当点 N 在CB 上时,由 解得 舍去了负值).
② 当点M、N在AB 上时, 12,点O到AB 的距离为
(i) 如图5,点M、N 在相遇前,
由 解得t=8.
(ii) 如图6,点 M、N 在相遇后,MN=3t-28.
由 解得
9.满分解答
(1)如图2,作AF⊥BC于F.
在Rt△ABF 中, 所以BF=2.所以.
在Rt△ACF中,CF=BC-BF=9--2=7,所以,
(2)如图3,作CG⊥AB于G,作OH⊥AB 于H,那么(
在Rt△BCG中,. 所以BG=3.
所以CG=6 ,AG=3.所以(
如图4,在 Rt△OPH 中,
由勾股定理,得
整理,得
定义域是0
由OH⊥AB,可知 H 是AE 的中点.
又因为 P 是BE 的中点,所以
在Rt△OPH 中, PH =3,OH =3 所以
如图7,特别地,当点 E 与点A 重合时,
考点伸展
第(1)题求 AC的长,用图3来解更便捷.
在Rt△BCG 中求得BG=3,可得CG 垂直平分AB,所以AC=BC=9.
10满分解答
(1) 如图2,由AB=AC,得∠1=∠2.
由EF=EC,得∠EFC=∠ECF.
所以∠EFC-∠1=∠ECF--∠2,即∠3=∠4.
又因为∠EAP=∠CAE,所以△AEP∽△ACE.
所以 所以
(2) 第一步,求△ECB 的面积.
如图3,作EH⊥BC于H,那么EH 垂直平分FC,所以
在Rt△EBH 中, 所以
所以
第二步,证明△PFC∽△ECB.
如图4,由∠2=∠1,∠EFC=∠ECF,得△PFC∽△ECB.
所以 所以
定义域是0
在Rt△ABM中, 所以AM=1.
所以
① 如图6,当点 P 在BC 上时,如果 那么P是EF 的中点.
已知FE=CE,所以
由于△AEP∽△ACE,所以
所以 此时
② 如图7,当点 P 在BC 的延长线上时,如果 那么
同样的,△AEP ∽△ACE,所以
所以 此时
考点伸展
第(3)题也可以由△PFC∽△ECB 来解.
如图8所示,由 得BC=2CF=2x.
过点 E 作BC 的平行线交CA 的延长线于N.
①如图8,当点 P 在BC 上时,如果 那么 P 是EF 的中点.
所以NE=CF=x.
由 得 所以
②如图9,当点 P 在BC 的延长线上时,如果 那么 所以
由 得 所以
同课章节目录
