四川省成都市蓉城名校联盟2025届高三上学期第一次联合诊断性考试 数学(含答案)
文档属性
| 名称 | 四川省成都市蓉城名校联盟2025届高三上学期第一次联合诊断性考试 数学(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-30 08:41:43 | ||
图片预览




文档简介
1
四川省高三年级第一次联合诊断性考试
数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的姓名、座位号、考籍号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“贴条形码区”.
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效.
3.考试结束后由监考老师将答题卡收回.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合,,则().
A. 或 B.
C. 或 D.
2. 在复平面内,复数对应的点位于第二象限,则实数a的取值范围为().
A. B. C. D.
3. 已知,设甲:;乙:,则甲是乙的().
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
4. 已知平面向量,,则在上的投影向量为().
A. B. C. D.
5. 在年巴黎奥运会上,我国网球选手郑钦文历经场比赛,勇夺巴黎奥运会女子网球单打冠军,书写了中国网球新的历史.某学校有名学生,一机构在该校随机抽取了名学生对郑钦文奥运会期间场单打比赛的收看情况进行了调查,将数据分组整理后,列表如下:
观看场次
观看人数占调查人数的百分比
从表中数据可以得出的正确结论为().
A. 表中的数值为
B. 观看场次不超过场的学生的比例为
C. 估计该校观看场次不超过场的学生约为人
D. 估计该校观看场次不低于场的学生约为人
6. 已知的内角A,B,C的对边分别为a,b,c,且,则().
A. B. C. D.
7. 设双曲线的离心率为,实轴长为2,则双曲线C上任意一点到双曲线C的两条渐近线的距离的乘积为().
A. B. C. D.
8. 已知函数,且为偶函数,则满足不等式的实数m的取值范围为().
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错的得0分.
9. 已知函数,则().
A. 最小正周期为
B. 在上单调递增
C. 的图象关于直线对称
D. 的图象可由的图象向左平移个单位得到
10. 已知椭圆的左、右焦点分别为,,过点的直线与椭圆E相交于P,Q两点,则().
A. 以椭圆E长轴为直径的圆的方程为
B. 以为直径的圆与椭圆E有且仅有2个公共点
C. 以为圆心,为半径圆与椭圆E有3个公共点
D. 以为直径的圆与直线相离
11. 如图,在正方体中,O是线段的中点,点P在棱上运动,则().
A. 点P在平面上的射影不可能是点O
B. 点P在平面上的射影到B,D两点的距离相等
C. 当点P与顶点A重合时,直线与平面所成角正切值为
D. 当点P与顶点重合时,点P到平面的距离等于
三、填空题:本大题共3小题,每小题5分,共15分.
12. 已知,且,则__________.
13. 甲、乙、丙、丁、戊5人站成两排照相,前排站2人,后排站3人,其中甲和乙须左右相邻,丙不站前排,则不同站法共有__________种(用数字作答).
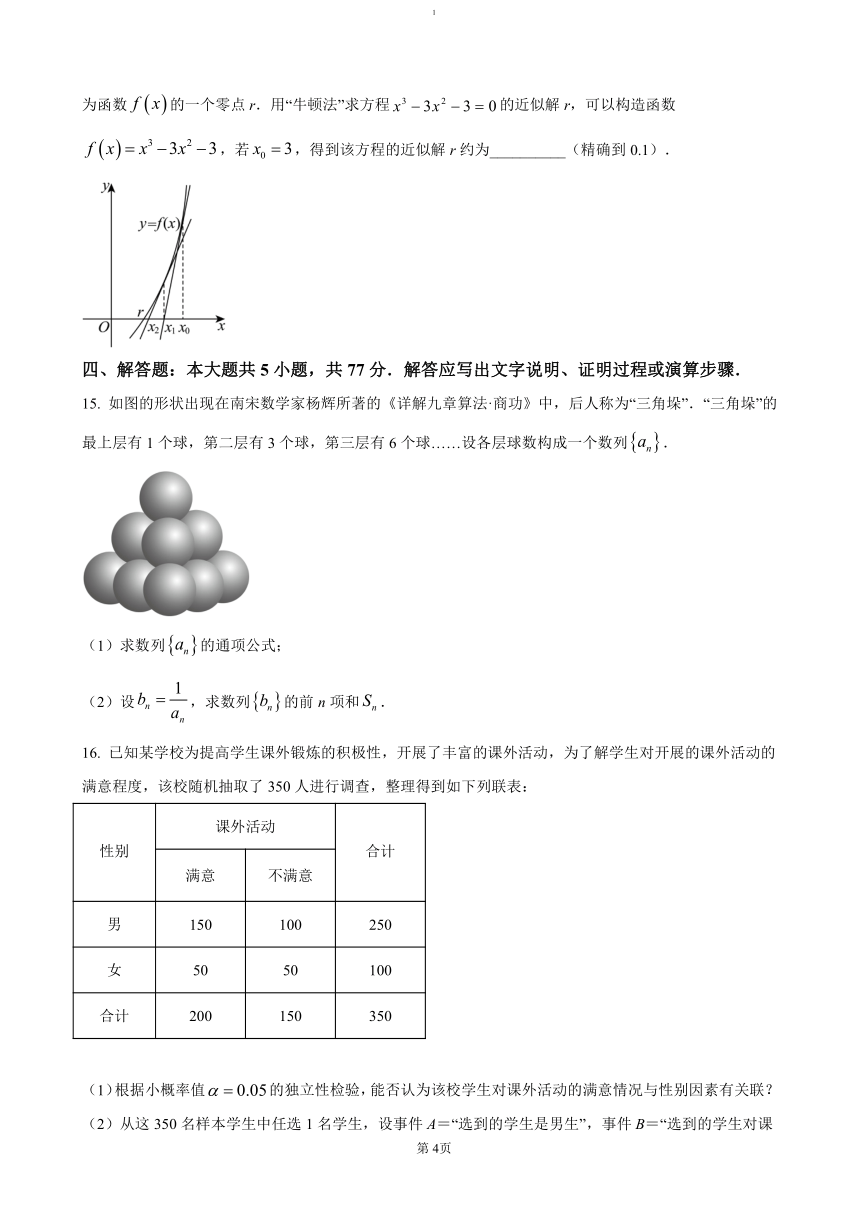
14. 人们很早以前就开始探索高次方程的数值求解问题,牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法——牛顿法,如图,在横坐标为的点处作的切线,该切线与x轴的交点为;在横坐标为的点处的切线与x轴的交点为;一直继续下去,得到,,,…,,它们越来越逼近的零点r.在一定精确度下,用四舍五入法取值,当,近似值相等时,该值可作为函数的一个零点r.用“牛顿法”求方程的近似解r,可以构造函数,若,得到该方程的近似解r约为__________(精确到0.1).
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 如图的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中,后人称为“三角垛”.“三角垛”的最上层有1个球,第二层有3个球,第三层有6个球……设各层球数构成一个数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
16. 已知某学校为提高学生课外锻炼的积极性,开展了丰富的课外活动,为了解学生对开展的课外活动的满意程度,该校随机抽取了350人进行调查,整理得到如下列联表:
性别 课外活动 合计
满意 不满意
男 150 100 250
女 50 50 100
合计 200 150 350
(1)根据小概率值的独立性检验,能否认为该校学生对课外活动的满意情况与性别因素有关联?
(2)从这350名样本学生中任选1名学生,设事件A=“选到的学生是男生”,事件B=“选到的学生对课外活动满意”,比较和的大小,并解释其意义,
附:
0.1 0.05 0.01
2.706 3.841 6.635
17. 如图,在几何体中,四边形是梯形,,,与相交于点N,平面,,H是的中点,,.
(1)点P在上,且,证明:平面;
(2)求二面角的余弦值.
18. 已知为抛物线的焦点,过点的直线与抛物线相交于,两点.
(1)证明:是常数;
(2)过点作直线的垂线与抛物线的准线相交于点,与抛物线相交于,两点(点的横坐标小于点的横坐标).
①求的值;
②是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
19. 已知函数.
(1)若,求函数的极值;
(2)若,,求实数a的取值范围;
(3)若,且,证明:.
四川省高三年级第一次联合诊断性考试
数学
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】D
2.
【答案】A
3.
【答案】B
4.
【答案】B
5.
【答案】D
6.
【答案】C
7.
【答案】B
8.
【答案】C
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错的得0分.
9.
【答案】AC
10.
【答案】ABD
11.
【答案】BCD
三、填空题:本大题共3小题,每小题5分,共15分.
12.
【答案】
13.
【答案】20
14.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.
【解析】
【分析】(1)由题意得到递推关系,再时,利用累加法结合等差数列的前项和公式求出即可;
(2)用裂项相消法求和即可.
【小问1详解】
由题意可知,
,,,……
,
数列的一个递推关系为,,
当时,利用累加法可得,
,
将代入得,满足,
所以数列的通项公式为,.
【小问2详解】
由(①)知,,
则
.
16.
【解析】
【分析】(1)同过列联表中数据计算的值,再与小概率值进行比较得出结论;
(2)根据条件概率公式本别计算和的值并比较两值的大小,并根据条件概率的含义说明所得结论在本题对应的意义.
【小问1详解】
提出零假设:该校学生对课外活动的满意情况与性别因素无关联,
根据表中数据,得到,
所以根据小概率值的独立性检验,没有充分证据推断不成立,
即认为该校学生对课外活动的满意情况与性别因素无关联.
【小问2详解】
解法1:依题意得,,
,
则.
解法2:依题意得,,,
,,
所以,,
则.
意义:男生对课外活动满意的概率比女生对课外活动满意的概率大;或者男生对课外活动满意的人数比女生对课外活动满意的人数多等等.
17.
【解析】
【分析】(1)添加辅助线,利用线段长度的比例关系证明线线平行,再利用线面平行的判定定理证明即可;也可根据垂直关系建立空间直角坐标系,利用空间向量证明线面平行.
(2)分别求出二面角的两半平面的法向量,利用二面角的向量公式计算即可.
【小问1详解】
方法1:依题意可知,直线,,两两垂直,以点A为坐标原点,
直线,,分别为x,y,z轴,建立如图所示的空间直角坐标系,
依题意得,,,,
因为,所以,所以,
又,所以,
又,,从而得,
所以向量,,共面,
又平面,平面,平面,
所以平面.
方法2:如图,,上取点M,Q,且满足,,
连接,,,
因为,,有,
所以,且,
又因为,,,
所以,有,
所以,且,
又,所以,且,
所以四边形为平行四边形,所以,
又平面,平面,
所以平面.
【小问2详解】
由(1)方法1可知,,,,
设平面的法向量为,
则,即,
取,则平面的一个法向量为,
设平面的法向量为,
则,即.
取,则平面的一个法向量为,
则,
由图知二面角为钝角,
故二面角的余弦值为.
18.
【解析】
【分析】(1)设出直线的方程并与抛物线方程联立,利用根与系数关系证得.
(2)①求得直线的方程,点的坐标,利用根与系数关系求得.
②根据抛物线的定义求得,然后求得的表达式,再利用不基本不等式求得最小值.或:假设直线的倾斜角为,将表示为含有的三角函数的形式,利用换元法、函数的单调性等知识来求得最小值.
【小问1详解】
由已知,点的坐标为,且可设直线的方程为,
联立方程组,消去,
得(*),
因为,
所以,为方程(*)的两个实根,且,
因为点,在抛物线上,
所以,为常数.
【小问2详解】
在题设条件下,直线,都不与坐标轴平行且,
由(1)可知直线的方程为:,
①因为抛物线的准线方程为,
代入的方程可得点的坐标为,
由(1)可知,,,
,,
因此,,
,
即的值为.
②存在最小值,
设点,的坐标分别为,,
因为点均在抛物线上,
所以,,,,
由,有,即,
变形可得,
则(**),
同理,,
根据抛物线的定义可知,,,
,,
所以
.
由(**)知,,
即,当且仅当时取“=”,
同理,,当且仅当时取“=”,
由题设,,
所以,,
所以,
,
由题意可知,,同时成立,
此时,取得最小值,
故存在最小值,最小值为.
另解:
存在最小值,
假设直线的倾斜角为,根据题意可设,
如图,设点在轴上的射影为点,
抛物线的准线与轴相交于点,
根据抛物线的定义,由题设点的位置可知
,
所以,,
同理可得,,,,
所以
,
令,,
则,
由,可得,
易知函数为增函数,
所以,
上式中,当且仅当,即时(此时)等号成立,
所以,,
所以,存在最小值,该最小值当且仅当时取得.
19.
【解析】
【分析】(1)根据题意,求导即可得到函数的单调性,从而得到其极值;
(2)根据题意,令,将问题转化为最值问题,然后求导可得,然后分与讨论,即可得到结果;
(3)结合对数的运算可得只需证明,再由(2)中结论可得,代入计算,即可证明.
小问1详解】
当时,,
令,即,则,
当时,,单调递增,
当时,,单调递减,
当时,,单调递增,
所以,当时,取得极大值,
当时,取得极小值.
【小问2详解】
令,
则,且,,
设,则,
又令,则,
①若,即时,
由于在区间上为增函数,可知,
则即在区间上为增函数,故,
所以即在区间上为增函数,
则,则在区间上为增函数,
所以,即时,恒成立,
所以,当时,符合条件.
②若,即时,
由于为单调递增函数,且,
所以,,
则时,,
可知)即在区间上为减函数,则,
故即在区间上为减函数,则,
则在区间上为减函数,所以,不符合题意,
综上所述,当,时,a的取值范围为.
【小问3详解】
欲证,
只需证明,
由(2)可知,当时,,即有,
进而得,其中,当且仅当时“=”成立,
则,,…,,
所以
,
所以.
PAGE
第18页
四川省高三年级第一次联合诊断性考试
数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的姓名、座位号、考籍号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“贴条形码区”.
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效.
3.考试结束后由监考老师将答题卡收回.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合,,则().
A. 或 B.
C. 或 D.
2. 在复平面内,复数对应的点位于第二象限,则实数a的取值范围为().
A. B. C. D.
3. 已知,设甲:;乙:,则甲是乙的().
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
4. 已知平面向量,,则在上的投影向量为().
A. B. C. D.
5. 在年巴黎奥运会上,我国网球选手郑钦文历经场比赛,勇夺巴黎奥运会女子网球单打冠军,书写了中国网球新的历史.某学校有名学生,一机构在该校随机抽取了名学生对郑钦文奥运会期间场单打比赛的收看情况进行了调查,将数据分组整理后,列表如下:
观看场次
观看人数占调查人数的百分比
从表中数据可以得出的正确结论为().
A. 表中的数值为
B. 观看场次不超过场的学生的比例为
C. 估计该校观看场次不超过场的学生约为人
D. 估计该校观看场次不低于场的学生约为人
6. 已知的内角A,B,C的对边分别为a,b,c,且,则().
A. B. C. D.
7. 设双曲线的离心率为,实轴长为2,则双曲线C上任意一点到双曲线C的两条渐近线的距离的乘积为().
A. B. C. D.
8. 已知函数,且为偶函数,则满足不等式的实数m的取值范围为().
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错的得0分.
9. 已知函数,则().
A. 最小正周期为
B. 在上单调递增
C. 的图象关于直线对称
D. 的图象可由的图象向左平移个单位得到
10. 已知椭圆的左、右焦点分别为,,过点的直线与椭圆E相交于P,Q两点,则().
A. 以椭圆E长轴为直径的圆的方程为
B. 以为直径的圆与椭圆E有且仅有2个公共点
C. 以为圆心,为半径圆与椭圆E有3个公共点
D. 以为直径的圆与直线相离
11. 如图,在正方体中,O是线段的中点,点P在棱上运动,则().
A. 点P在平面上的射影不可能是点O
B. 点P在平面上的射影到B,D两点的距离相等
C. 当点P与顶点A重合时,直线与平面所成角正切值为
D. 当点P与顶点重合时,点P到平面的距离等于
三、填空题:本大题共3小题,每小题5分,共15分.
12. 已知,且,则__________.
13. 甲、乙、丙、丁、戊5人站成两排照相,前排站2人,后排站3人,其中甲和乙须左右相邻,丙不站前排,则不同站法共有__________种(用数字作答).
14. 人们很早以前就开始探索高次方程的数值求解问题,牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法——牛顿法,如图,在横坐标为的点处作的切线,该切线与x轴的交点为;在横坐标为的点处的切线与x轴的交点为;一直继续下去,得到,,,…,,它们越来越逼近的零点r.在一定精确度下,用四舍五入法取值,当,近似值相等时,该值可作为函数的一个零点r.用“牛顿法”求方程的近似解r,可以构造函数,若,得到该方程的近似解r约为__________(精确到0.1).
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 如图的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中,后人称为“三角垛”.“三角垛”的最上层有1个球,第二层有3个球,第三层有6个球……设各层球数构成一个数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
16. 已知某学校为提高学生课外锻炼的积极性,开展了丰富的课外活动,为了解学生对开展的课外活动的满意程度,该校随机抽取了350人进行调查,整理得到如下列联表:
性别 课外活动 合计
满意 不满意
男 150 100 250
女 50 50 100
合计 200 150 350
(1)根据小概率值的独立性检验,能否认为该校学生对课外活动的满意情况与性别因素有关联?
(2)从这350名样本学生中任选1名学生,设事件A=“选到的学生是男生”,事件B=“选到的学生对课外活动满意”,比较和的大小,并解释其意义,
附:
0.1 0.05 0.01
2.706 3.841 6.635
17. 如图,在几何体中,四边形是梯形,,,与相交于点N,平面,,H是的中点,,.
(1)点P在上,且,证明:平面;
(2)求二面角的余弦值.
18. 已知为抛物线的焦点,过点的直线与抛物线相交于,两点.
(1)证明:是常数;
(2)过点作直线的垂线与抛物线的准线相交于点,与抛物线相交于,两点(点的横坐标小于点的横坐标).
①求的值;
②是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
19. 已知函数.
(1)若,求函数的极值;
(2)若,,求实数a的取值范围;
(3)若,且,证明:.
四川省高三年级第一次联合诊断性考试
数学
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】D
2.
【答案】A
3.
【答案】B
4.
【答案】B
5.
【答案】D
6.
【答案】C
7.
【答案】B
8.
【答案】C
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错的得0分.
9.
【答案】AC
10.
【答案】ABD
11.
【答案】BCD
三、填空题:本大题共3小题,每小题5分,共15分.
12.
【答案】
13.
【答案】20
14.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.
【解析】
【分析】(1)由题意得到递推关系,再时,利用累加法结合等差数列的前项和公式求出即可;
(2)用裂项相消法求和即可.
【小问1详解】
由题意可知,
,,,……
,
数列的一个递推关系为,,
当时,利用累加法可得,
,
将代入得,满足,
所以数列的通项公式为,.
【小问2详解】
由(①)知,,
则
.
16.
【解析】
【分析】(1)同过列联表中数据计算的值,再与小概率值进行比较得出结论;
(2)根据条件概率公式本别计算和的值并比较两值的大小,并根据条件概率的含义说明所得结论在本题对应的意义.
【小问1详解】
提出零假设:该校学生对课外活动的满意情况与性别因素无关联,
根据表中数据,得到,
所以根据小概率值的独立性检验,没有充分证据推断不成立,
即认为该校学生对课外活动的满意情况与性别因素无关联.
【小问2详解】
解法1:依题意得,,
,
则.
解法2:依题意得,,,
,,
所以,,
则.
意义:男生对课外活动满意的概率比女生对课外活动满意的概率大;或者男生对课外活动满意的人数比女生对课外活动满意的人数多等等.
17.
【解析】
【分析】(1)添加辅助线,利用线段长度的比例关系证明线线平行,再利用线面平行的判定定理证明即可;也可根据垂直关系建立空间直角坐标系,利用空间向量证明线面平行.
(2)分别求出二面角的两半平面的法向量,利用二面角的向量公式计算即可.
【小问1详解】
方法1:依题意可知,直线,,两两垂直,以点A为坐标原点,
直线,,分别为x,y,z轴,建立如图所示的空间直角坐标系,
依题意得,,,,
因为,所以,所以,
又,所以,
又,,从而得,
所以向量,,共面,
又平面,平面,平面,
所以平面.
方法2:如图,,上取点M,Q,且满足,,
连接,,,
因为,,有,
所以,且,
又因为,,,
所以,有,
所以,且,
又,所以,且,
所以四边形为平行四边形,所以,
又平面,平面,
所以平面.
【小问2详解】
由(1)方法1可知,,,,
设平面的法向量为,
则,即,
取,则平面的一个法向量为,
设平面的法向量为,
则,即.
取,则平面的一个法向量为,
则,
由图知二面角为钝角,
故二面角的余弦值为.
18.
【解析】
【分析】(1)设出直线的方程并与抛物线方程联立,利用根与系数关系证得.
(2)①求得直线的方程,点的坐标,利用根与系数关系求得.
②根据抛物线的定义求得,然后求得的表达式,再利用不基本不等式求得最小值.或:假设直线的倾斜角为,将表示为含有的三角函数的形式,利用换元法、函数的单调性等知识来求得最小值.
【小问1详解】
由已知,点的坐标为,且可设直线的方程为,
联立方程组,消去,
得(*),
因为,
所以,为方程(*)的两个实根,且,
因为点,在抛物线上,
所以,为常数.
【小问2详解】
在题设条件下,直线,都不与坐标轴平行且,
由(1)可知直线的方程为:,
①因为抛物线的准线方程为,
代入的方程可得点的坐标为,
由(1)可知,,,
,,
因此,,
,
即的值为.
②存在最小值,
设点,的坐标分别为,,
因为点均在抛物线上,
所以,,,,
由,有,即,
变形可得,
则(**),
同理,,
根据抛物线的定义可知,,,
,,
所以
.
由(**)知,,
即,当且仅当时取“=”,
同理,,当且仅当时取“=”,
由题设,,
所以,,
所以,
,
由题意可知,,同时成立,
此时,取得最小值,
故存在最小值,最小值为.
另解:
存在最小值,
假设直线的倾斜角为,根据题意可设,
如图,设点在轴上的射影为点,
抛物线的准线与轴相交于点,
根据抛物线的定义,由题设点的位置可知
,
所以,,
同理可得,,,,
所以
,
令,,
则,
由,可得,
易知函数为增函数,
所以,
上式中,当且仅当,即时(此时)等号成立,
所以,,
所以,存在最小值,该最小值当且仅当时取得.
19.
【解析】
【分析】(1)根据题意,求导即可得到函数的单调性,从而得到其极值;
(2)根据题意,令,将问题转化为最值问题,然后求导可得,然后分与讨论,即可得到结果;
(3)结合对数的运算可得只需证明,再由(2)中结论可得,代入计算,即可证明.
小问1详解】
当时,,
令,即,则,
当时,,单调递增,
当时,,单调递减,
当时,,单调递增,
所以,当时,取得极大值,
当时,取得极小值.
【小问2详解】
令,
则,且,,
设,则,
又令,则,
①若,即时,
由于在区间上为增函数,可知,
则即在区间上为增函数,故,
所以即在区间上为增函数,
则,则在区间上为增函数,
所以,即时,恒成立,
所以,当时,符合条件.
②若,即时,
由于为单调递增函数,且,
所以,,
则时,,
可知)即在区间上为减函数,则,
故即在区间上为减函数,则,
则在区间上为减函数,所以,不符合题意,
综上所述,当,时,a的取值范围为.
【小问3详解】
欲证,
只需证明,
由(2)可知,当时,,即有,
进而得,其中,当且仅当时“=”成立,
则,,…,,
所以
,
所以.
PAGE
第18页
同课章节目录
