2025高考物理二轮复习专题二-功和能、动量-第2讲 滑块一木板模型综合问题 课件 (共42张PPT)
文档属性
| 名称 | 2025高考物理二轮复习专题二-功和能、动量-第2讲 滑块一木板模型综合问题 课件 (共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-30 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
第2讲 滑块一木板模型综合问题
角度1 系统动量不守恒
角度2 系统动量守恒
跟踪训练
备用习题
1.模型特点:摩擦力的分析与“传送带”模型类似,木板受到摩擦力的影响,往
往做匀变速直线运动,解决此类问题要注意从速度、位移、时间等角度寻
找各运动过程之间的联系.
2.解题关键:(1)抓住临界条件,使滑块不从木板的末端掉下来的临界条件是
滑块到达木板末端时的速度与木板的速度恰好相同.(2)抓住问题实质,“滑
块—木板”模型的本质是相对运动问题,一是分析共速时是否发生相对运动,
采用假设法判断摩擦力是静摩擦力还是滑动摩擦力,二是要分别求出滑块
和木板对地的位移,再计算相对位移.
角度1 系统动量不守恒
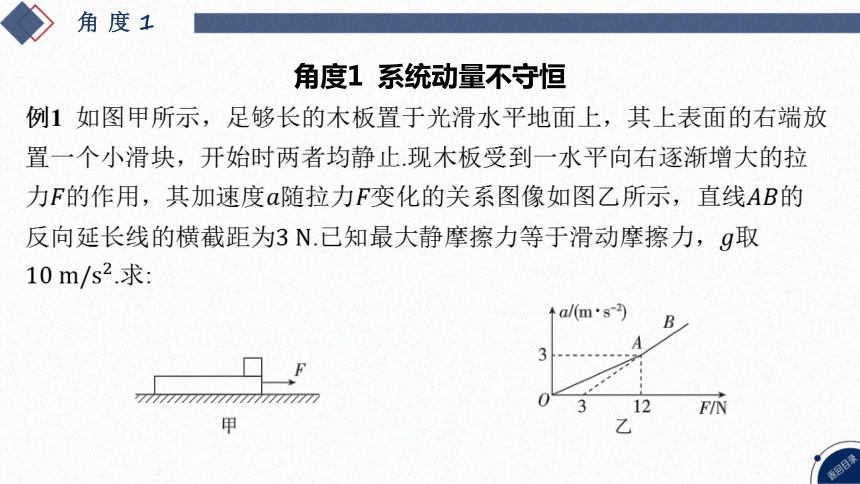
例1 如图甲所示,足够长的木板置于光滑水平地面上,其上表面的右端放
置一个小滑块,开始时两者均静止.现木板受到一水平向右逐渐增大的拉
力的作用,其加速度随拉力变化的关系图像如图乙所示,直线 的
反向延长线的横截距为.已知最大静摩擦力等于滑动摩擦力, 取
.求:
(1) 木板与滑块之间的动摩擦因数 ;
[答案] 0.3
[解析] 根据图像可知,当拉力满足 时,滑块和木板保持相
对静止一起向右加速运动,当拉力 时,滑块和木板发生相对滑动,
所以木板和滑块恰好发生相对滑动时,加速度
对滑块,根据牛顿第二定律有
解得
(2) 木板的质量和滑块的质量 .
[答案] ;
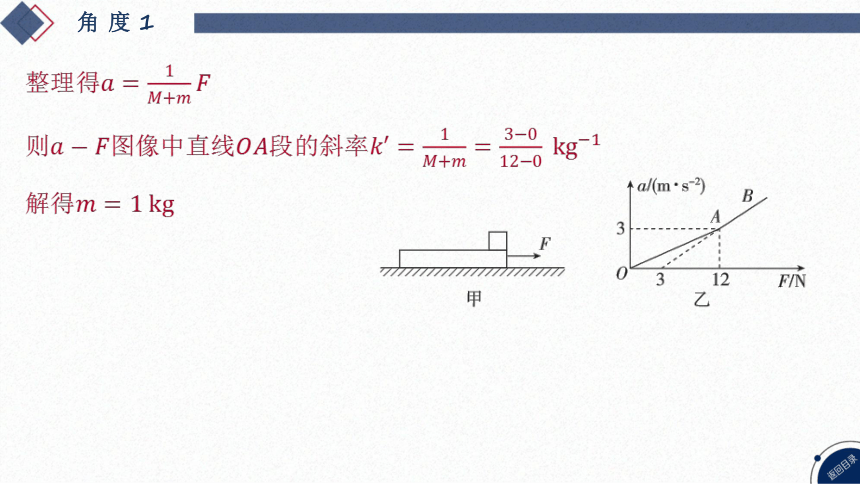
[解析] 当拉力时,
对木板,根据牛顿第二定律有
整理得
则图像中直线段的斜率
解得
当拉力满足 时,对整体,根据牛顿第二定律有
整理得
则图像中直线段的斜率
解得
变式 (不定项)如图所示, 为质量不计的足够长的硬质膜,放在光滑的水
平面上,其上分别静止放有两个物体和,的质量为, 的质量
,与膜之间的动摩擦因数均为 ,物体受到的最大静摩擦力等于
其滑动摩擦力.的水平拉力在时刻开始作用在物体上, 取
.下列说法正确的是( )
A.若力水平向右作用在物体上,则物体的加速度大小为
B.若力水平向右作用在物体上,后撤去力,则物体 最终的速度大
小为
C.若力水平向左作用在物体上,则物体的加速度大小为
D.若力水平向左作用在物体上,后撤去力,则物体 最终的速度大
小为
√
√
√
[解析] 根据题意可知,A与C之间的最大静摩擦力为 ,
B与C之间的最大静摩擦力为 ,由于C的质量不计,
则C的合力一定为0,即A与C之间和B与C之间的摩擦力大小相等,根据题
意,若力 水平向右作用在物体A上,由于物体B的最大加速度为
,对整体有 ,
可知B与C之间发生相对滑动,由牛顿第二定律,对物体A有
,解得, 后,物体A的速度为
,物体B的速度为,撤去力 后,
A、B、C组成的系统动量守恒,最终三者共速,则有
,解得 ,故A错误,B正确;
根据题意,若力 水平向左作用在物体B上,则B与C之间发生相对滑动,
由牛顿第二定律,对物体B有,解得 ,对
物体A有,解得, 后,物体A的速度为
,物体B的速度为,撤去力 后,A、
B、C组成的系统动量守恒,最终三者共速,则有
,解得 ,故C、D正确.
角度2 系统动量守恒
例2 (不定项)[2024·湖北孝感模拟] 如图所示,在光滑水平面上,有一质
量的薄板和质量的物块都以 的初速度相向运
动,它们之间有摩擦,且动摩擦因数为 ,薄板足够长,下列说法正确
的是( )
A.当薄板的速度为 时,物块正在向左运动,
且正在减速
B.物块向左滑行的最大位移约为
C.物块相对于木板的位移约为
D.物块与木板之间因摩擦产生的热量为
√
√
[解析] 取薄板运动方向为正方向,设薄板和物
块共速时的速度大小为 ,薄板和物块组成的
系统动量守恒,有 ,解
得 ,故薄板向右做减速运动,物块
先向左减速运动,速度减到零后向右加速运动,
最终薄板和物块一起向右运动,当薄板速度大
小为时,设此时物块的速度为 ,
根据动量守恒定律得 ,
解得 ,即此时物块正在向左减速运
动,故A正确;对物块,根据牛顿第二定律得
,当物块
对地速度为0时,向左滑行的位移最大,为
,故B错误;薄板
和物块相对运动的整个过程,根据能量守恒定
律得
,
解得, ,故C错误,D正确.
例3 [2024·嘉兴模拟] 如图所示,放在光滑水
平面上的小车可以在两个固定障碍物、 之
间往返运动.小车最左端放有一个小木块,初
始小车紧挨障碍物静止.某时刻,一粒子弹以 的速度射中木
块并嵌入其中.小车向右运动到与障碍物 相碰时,木块恰好运动到小车的
最右端,且小车与木块恰好达到共速. 小车和它上面的木块同时与障碍物
相碰,碰后小车速度立即减为零,而木块以碰撞之前的速率反弹.过一段
时间,小车左端又与障碍物 相碰,碰后小车速度立即减为零,木块继续
在小车上向左滑动,速度逐渐减为零而停在小
车上.已知小车质量为,长度为 ,
小木块质量为,子弹质量为 ,子弹和
小木块都可以看作质点,取 .求:
(1) 小木块运动过程中的最大速度;
[答案]
[解析] 小木块在小车上滑动时做减速运动,
因此小木块的最大速度为子弹射入木块后的共
同速度,设子弹和小木块的共同速度为 ,以
向右为正方向,根据动量守恒定律有
解得小木块的最大速度为
(2) 小木块与小车间的动摩擦因数;
[答案] 0.36
[解析] 将内嵌子弹的小木块与小车看作整体,
系统动量守恒,设整体与障碍物 相碰时达到
的共同速度为 ,由动量守恒定律得
解得
设小木块与小车之间的摩擦力为,动摩擦因数为 ,对三者组成的系统,
由能量守恒定律得
其中
联立解得
(3) 小木块最终停止运动后,小木块在小车上的位置与小车右端的距离.
[答案]
[解析] 设小木块反弹后与小车达到相对静止
状态时共同速度为 ,相对小车滑动的距离
为 ,小车停下后小木块做匀减速运动,相对
小车滑行的距离为 ,小木块反弹后,对三者
组成的系统,由动量守恒定律得
由能量守恒定律得
小车停下后,对小木块,由动能定理得
解得,
所以小木块最终停止运动后,小木块在小车
上的位置与小车右端的距离为
1. 将一盒未开封的香皂置于桌面上的一张纸板上,用水平向右的拉力将纸板迅速抽出,香皂盒(包括香皂)的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验(示意图如图所示).设香皂盒和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ,重力加速度为g.在本实验中,m1=100 g,m2=5 g,μ=0.2,g取10 m/s2,香皂盒与纸板左端的距离d=0.1 m.若香皂盒移动的距离超过l=0.002 m,人眼就能感知,忽略香皂盒的体积因素影响,为确保香皂盒移动不被人感知,纸板所需的拉力至少是( )
A.1.41 N B.1.42 N
C.1410 N D.1420 N
√
[解析] 香皂盒在纸板上滑动过程中,香皂盒的加速度a1==μg=2 m/s2,纸板的加速度a2= ,香皂盒的位移x1=a1,纸板的位移x'=x1+d=a2,纸板抽出后,香皂盒的位移x2=a3 ,其中a3=a1,由题意知a1t1=a3t2,l=x1+x2,联立解得F=1.42 N,故B正确.
2. (多选) 如图所示,一质量为M、长为l的木板静止在光滑水平桌面上,另一质量为m的小物块(可视为质点)从木板上的左端以速度v0开始运动.已知物块与木板间的滑动摩擦力大小为Ff,当物块从木板右端离开时 ( )
A.木板的动能一定等于Ffl
B.木板的动能一定小于Ffl
C.物块的动能一定大于m-Ffl
D.物块的动能一定小于m-Ffl
√
√
[解析] 设物块在木板上运动t1时间后离开木板,在这段时间内物块在摩擦力的作用力下做匀减速直线运动,木板在摩擦力的作用力下做匀加速直线运动,它们这段时间内的v-t图像如图所示,AB为物块的v-t图像,OC为木板的v-t图像.结合题意可知梯形OABC的面积表示木板长度l,三角形OCD的面积表示木板的位移,S△OCD
S梯OABC,即物块的位移x2>l,此过程中对木板由动能定理有Ffx1=Ek1-0,所以当物块从右端离开木板时木板的动能Ek1=Ffx1对物块由动能定理有-Ffx2=Ek2-m,所以当物块从右端离开
木板时物块的动能Ek2=m-Ffx21.(不定项)[2024·镇海中学模拟] 如图所示,质
量为的木板 静止放在光滑水平面上,
木板右端点处固定一根轻质弹簧,弹簧处于原长状态时左端在点, 点
到木板左端的距离,可视为质点的小木块质量为 ,静止放置在
木板的左端.现对木板施加水平向左的恒力, 时撤去恒力
,此时木块恰好到达弹簧自由端 处,此后的运动中没有超过弹簧的弹
性限度.已知木板上点左侧部分与木块间的动摩擦因数为, 点右
侧部分光滑,取 .下列说法正确的是 ( )
A.撤去恒力 后,木板先做减速运动,后做匀
速运动
B.恒力对木板做功为
C.整个运动过程中,弹簧的最大弹性势能为
D.整个运动过程中,系统产生的热量为
√
√
[解析] 恒力 作用的过程中,对小木块有
, ,联立解得
, ,对木板有
,, ,
联立解得, ,
,则恒力对木板 做功为
,此时木板的速度
,小木块的速度
,所以撤去恒力 后,弹簧被
压缩,小木块继续做加速运动,木板开始做减
速运动,弹簧压缩到最短时,两者共速,此时
弹簧的弹性势能最大,由动量守恒定律有
,由能量守恒定律有
,联立解
得, ,之后弹簧压缩量减小,
小木块继续做加速运动,木板继续做减速运动,
弹簧恢复原长时,小木块速度大于木板速度,
小木块接着向左运动进入粗糙面,开始做减速
运动,木板受到向左的摩擦力,开始做加速运
动,故B错误,C正确;弹簧恢复原长时,根据
动量守恒定律有 ,
根据能量守恒定律有
,联立解得
, ,假设二者在粗糙部
分最后共速,则由动量守恒定律有
,解得 ,
木板的加速度大小
,木板向左运动的位移
,小木块的
位移 ,由于
,故假设不成立,即小
木块会从木板左侧滑出,所以整个运动过程中,
系统产生的热量 ,故A错误,
D正确.
2.[2024·温州模拟] 如图甲所示,质量为、长度为 的木
板 静止在光滑水平面上(两表面与地面平行),在其右侧某一位置有一
竖直固定挡板.质量为的小物块(可视为质点)以 的初
速度从的最左端水平冲上,一段时间后与 发生弹性碰撞.以碰撞瞬间
为计时起点,取水平向右为正方向,碰后内的速度随时间 变化的
图像如图乙所示.重力加速度取 .
[解析] 由图像可知,第1次与碰前
瞬间的速度为 ,设此时
的速度,对、组成的系统,由动量守恒定律有
解得
由图像可知,内,的加速度大小
由牛顿第二定律有
解得
(1) 求刚冲上时挡板离 板右端的最小距离;
[答案]
由于,说明第1次与碰撞前,与已达到共速,设从滑上 到
与共速过程中的位移为,对由动能定理有
解得
所以挡板离板右端的最小距离为 .
(2) 求与 第1次碰撞到第2次碰撞的时间间隔内产生的热量;
[答案]
[解析] 设从滑上到与共速过程中的位移为,对 由动能定理有
解得
与第一次碰撞前,与 的相对位移
与 第1次碰后反弹,先向左做匀减速运动,后向右做匀加速运动,假设
与第2次碰前与已达到共速,此时速度为 ,以水平向右为正方向,
对、组成的系统,由动量守恒定律可得
解得
对 由动能定理得
由 由动能定理得
解得,
与碰后到与共速,与的相对位移
由于 ,所以假设成立.
与 第1次碰撞到第2次碰撞的时间间隔内产生的热量为
(3) 与碰撞几次,与 分离
[答案] 2次
[解析] 假设第3次碰撞前,与仍不分离,第2次与挡板碰后反弹至
与 再次共速的过程中,以水平向右为正方向,由动量守恒定律有
解得
由能量守恒定律有
解得
由于 ,故假设不成
立, 与未达到共速时即滑离 ,不能发生第3次碰撞
所以与碰撞2次,与 分离.
第2讲 滑块一木板模型综合问题
角度1 系统动量不守恒
角度2 系统动量守恒
跟踪训练
备用习题
1.模型特点:摩擦力的分析与“传送带”模型类似,木板受到摩擦力的影响,往
往做匀变速直线运动,解决此类问题要注意从速度、位移、时间等角度寻
找各运动过程之间的联系.
2.解题关键:(1)抓住临界条件,使滑块不从木板的末端掉下来的临界条件是
滑块到达木板末端时的速度与木板的速度恰好相同.(2)抓住问题实质,“滑
块—木板”模型的本质是相对运动问题,一是分析共速时是否发生相对运动,
采用假设法判断摩擦力是静摩擦力还是滑动摩擦力,二是要分别求出滑块
和木板对地的位移,再计算相对位移.
角度1 系统动量不守恒
例1 如图甲所示,足够长的木板置于光滑水平地面上,其上表面的右端放
置一个小滑块,开始时两者均静止.现木板受到一水平向右逐渐增大的拉
力的作用,其加速度随拉力变化的关系图像如图乙所示,直线 的
反向延长线的横截距为.已知最大静摩擦力等于滑动摩擦力, 取
.求:
(1) 木板与滑块之间的动摩擦因数 ;
[答案] 0.3
[解析] 根据图像可知,当拉力满足 时,滑块和木板保持相
对静止一起向右加速运动,当拉力 时,滑块和木板发生相对滑动,
所以木板和滑块恰好发生相对滑动时,加速度
对滑块,根据牛顿第二定律有
解得
(2) 木板的质量和滑块的质量 .
[答案] ;
[解析] 当拉力时,
对木板,根据牛顿第二定律有
整理得
则图像中直线段的斜率
解得
当拉力满足 时,对整体,根据牛顿第二定律有
整理得
则图像中直线段的斜率
解得
变式 (不定项)如图所示, 为质量不计的足够长的硬质膜,放在光滑的水
平面上,其上分别静止放有两个物体和,的质量为, 的质量
,与膜之间的动摩擦因数均为 ,物体受到的最大静摩擦力等于
其滑动摩擦力.的水平拉力在时刻开始作用在物体上, 取
.下列说法正确的是( )
A.若力水平向右作用在物体上,则物体的加速度大小为
B.若力水平向右作用在物体上,后撤去力,则物体 最终的速度大
小为
C.若力水平向左作用在物体上,则物体的加速度大小为
D.若力水平向左作用在物体上,后撤去力,则物体 最终的速度大
小为
√
√
√
[解析] 根据题意可知,A与C之间的最大静摩擦力为 ,
B与C之间的最大静摩擦力为 ,由于C的质量不计,
则C的合力一定为0,即A与C之间和B与C之间的摩擦力大小相等,根据题
意,若力 水平向右作用在物体A上,由于物体B的最大加速度为
,对整体有 ,
可知B与C之间发生相对滑动,由牛顿第二定律,对物体A有
,解得, 后,物体A的速度为
,物体B的速度为,撤去力 后,
A、B、C组成的系统动量守恒,最终三者共速,则有
,解得 ,故A错误,B正确;
根据题意,若力 水平向左作用在物体B上,则B与C之间发生相对滑动,
由牛顿第二定律,对物体B有,解得 ,对
物体A有,解得, 后,物体A的速度为
,物体B的速度为,撤去力 后,A、
B、C组成的系统动量守恒,最终三者共速,则有
,解得 ,故C、D正确.
角度2 系统动量守恒
例2 (不定项)[2024·湖北孝感模拟] 如图所示,在光滑水平面上,有一质
量的薄板和质量的物块都以 的初速度相向运
动,它们之间有摩擦,且动摩擦因数为 ,薄板足够长,下列说法正确
的是( )
A.当薄板的速度为 时,物块正在向左运动,
且正在减速
B.物块向左滑行的最大位移约为
C.物块相对于木板的位移约为
D.物块与木板之间因摩擦产生的热量为
√
√
[解析] 取薄板运动方向为正方向,设薄板和物
块共速时的速度大小为 ,薄板和物块组成的
系统动量守恒,有 ,解
得 ,故薄板向右做减速运动,物块
先向左减速运动,速度减到零后向右加速运动,
最终薄板和物块一起向右运动,当薄板速度大
小为时,设此时物块的速度为 ,
根据动量守恒定律得 ,
解得 ,即此时物块正在向左减速运
动,故A正确;对物块,根据牛顿第二定律得
,当物块
对地速度为0时,向左滑行的位移最大,为
,故B错误;薄板
和物块相对运动的整个过程,根据能量守恒定
律得
,
解得, ,故C错误,D正确.
例3 [2024·嘉兴模拟] 如图所示,放在光滑水
平面上的小车可以在两个固定障碍物、 之
间往返运动.小车最左端放有一个小木块,初
始小车紧挨障碍物静止.某时刻,一粒子弹以 的速度射中木
块并嵌入其中.小车向右运动到与障碍物 相碰时,木块恰好运动到小车的
最右端,且小车与木块恰好达到共速. 小车和它上面的木块同时与障碍物
相碰,碰后小车速度立即减为零,而木块以碰撞之前的速率反弹.过一段
时间,小车左端又与障碍物 相碰,碰后小车速度立即减为零,木块继续
在小车上向左滑动,速度逐渐减为零而停在小
车上.已知小车质量为,长度为 ,
小木块质量为,子弹质量为 ,子弹和
小木块都可以看作质点,取 .求:
(1) 小木块运动过程中的最大速度;
[答案]
[解析] 小木块在小车上滑动时做减速运动,
因此小木块的最大速度为子弹射入木块后的共
同速度,设子弹和小木块的共同速度为 ,以
向右为正方向,根据动量守恒定律有
解得小木块的最大速度为
(2) 小木块与小车间的动摩擦因数;
[答案] 0.36
[解析] 将内嵌子弹的小木块与小车看作整体,
系统动量守恒,设整体与障碍物 相碰时达到
的共同速度为 ,由动量守恒定律得
解得
设小木块与小车之间的摩擦力为,动摩擦因数为 ,对三者组成的系统,
由能量守恒定律得
其中
联立解得
(3) 小木块最终停止运动后,小木块在小车上的位置与小车右端的距离.
[答案]
[解析] 设小木块反弹后与小车达到相对静止
状态时共同速度为 ,相对小车滑动的距离
为 ,小车停下后小木块做匀减速运动,相对
小车滑行的距离为 ,小木块反弹后,对三者
组成的系统,由动量守恒定律得
由能量守恒定律得
小车停下后,对小木块,由动能定理得
解得,
所以小木块最终停止运动后,小木块在小车
上的位置与小车右端的距离为
1. 将一盒未开封的香皂置于桌面上的一张纸板上,用水平向右的拉力将纸板迅速抽出,香皂盒(包括香皂)的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验(示意图如图所示).设香皂盒和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ,重力加速度为g.在本实验中,m1=100 g,m2=5 g,μ=0.2,g取10 m/s2,香皂盒与纸板左端的距离d=0.1 m.若香皂盒移动的距离超过l=0.002 m,人眼就能感知,忽略香皂盒的体积因素影响,为确保香皂盒移动不被人感知,纸板所需的拉力至少是( )
A.1.41 N B.1.42 N
C.1410 N D.1420 N
√
[解析] 香皂盒在纸板上滑动过程中,香皂盒的加速度a1==μg=2 m/s2,纸板的加速度a2= ,香皂盒的位移x1=a1,纸板的位移x'=x1+d=a2,纸板抽出后,香皂盒的位移x2=a3 ,其中a3=a1,由题意知a1t1=a3t2,l=x1+x2,联立解得F=1.42 N,故B正确.
2. (多选) 如图所示,一质量为M、长为l的木板静止在光滑水平桌面上,另一质量为m的小物块(可视为质点)从木板上的左端以速度v0开始运动.已知物块与木板间的滑动摩擦力大小为Ff,当物块从木板右端离开时 ( )
A.木板的动能一定等于Ffl
B.木板的动能一定小于Ffl
C.物块的动能一定大于m-Ffl
D.物块的动能一定小于m-Ffl
√
√
[解析] 设物块在木板上运动t1时间后离开木板,在这段时间内物块在摩擦力的作用力下做匀减速直线运动,木板在摩擦力的作用力下做匀加速直线运动,它们这段时间内的v-t图像如图所示,AB为物块的v-t图像,OC为木板的v-t图像.结合题意可知梯形OABC的面积表示木板长度l,三角形OCD的面积表示木板的位移,S△OCD
S梯OABC,即物块的位移x2>l,此过程中对木板由动能定理有Ffx1=Ek1-0,所以当物块从右端离开木板时木板的动能Ek1=Ffx1
木板时物块的动能Ek2=m-Ffx2
量为的木板 静止放在光滑水平面上,
木板右端点处固定一根轻质弹簧,弹簧处于原长状态时左端在点, 点
到木板左端的距离,可视为质点的小木块质量为 ,静止放置在
木板的左端.现对木板施加水平向左的恒力, 时撤去恒力
,此时木块恰好到达弹簧自由端 处,此后的运动中没有超过弹簧的弹
性限度.已知木板上点左侧部分与木块间的动摩擦因数为, 点右
侧部分光滑,取 .下列说法正确的是 ( )
A.撤去恒力 后,木板先做减速运动,后做匀
速运动
B.恒力对木板做功为
C.整个运动过程中,弹簧的最大弹性势能为
D.整个运动过程中,系统产生的热量为
√
√
[解析] 恒力 作用的过程中,对小木块有
, ,联立解得
, ,对木板有
,, ,
联立解得, ,
,则恒力对木板 做功为
,此时木板的速度
,小木块的速度
,所以撤去恒力 后,弹簧被
压缩,小木块继续做加速运动,木板开始做减
速运动,弹簧压缩到最短时,两者共速,此时
弹簧的弹性势能最大,由动量守恒定律有
,由能量守恒定律有
,联立解
得, ,之后弹簧压缩量减小,
小木块继续做加速运动,木板继续做减速运动,
弹簧恢复原长时,小木块速度大于木板速度,
小木块接着向左运动进入粗糙面,开始做减速
运动,木板受到向左的摩擦力,开始做加速运
动,故B错误,C正确;弹簧恢复原长时,根据
动量守恒定律有 ,
根据能量守恒定律有
,联立解得
, ,假设二者在粗糙部
分最后共速,则由动量守恒定律有
,解得 ,
木板的加速度大小
,木板向左运动的位移
,小木块的
位移 ,由于
,故假设不成立,即小
木块会从木板左侧滑出,所以整个运动过程中,
系统产生的热量 ,故A错误,
D正确.
2.[2024·温州模拟] 如图甲所示,质量为、长度为 的木
板 静止在光滑水平面上(两表面与地面平行),在其右侧某一位置有一
竖直固定挡板.质量为的小物块(可视为质点)以 的初
速度从的最左端水平冲上,一段时间后与 发生弹性碰撞.以碰撞瞬间
为计时起点,取水平向右为正方向,碰后内的速度随时间 变化的
图像如图乙所示.重力加速度取 .
[解析] 由图像可知,第1次与碰前
瞬间的速度为 ,设此时
的速度,对、组成的系统,由动量守恒定律有
解得
由图像可知,内,的加速度大小
由牛顿第二定律有
解得
(1) 求刚冲上时挡板离 板右端的最小距离;
[答案]
由于,说明第1次与碰撞前,与已达到共速,设从滑上 到
与共速过程中的位移为,对由动能定理有
解得
所以挡板离板右端的最小距离为 .
(2) 求与 第1次碰撞到第2次碰撞的时间间隔内产生的热量;
[答案]
[解析] 设从滑上到与共速过程中的位移为,对 由动能定理有
解得
与第一次碰撞前,与 的相对位移
与 第1次碰后反弹,先向左做匀减速运动,后向右做匀加速运动,假设
与第2次碰前与已达到共速,此时速度为 ,以水平向右为正方向,
对、组成的系统,由动量守恒定律可得
解得
对 由动能定理得
由 由动能定理得
解得,
与碰后到与共速,与的相对位移
由于 ,所以假设成立.
与 第1次碰撞到第2次碰撞的时间间隔内产生的热量为
(3) 与碰撞几次,与 分离
[答案] 2次
[解析] 假设第3次碰撞前,与仍不分离,第2次与挡板碰后反弹至
与 再次共速的过程中,以水平向右为正方向,由动量守恒定律有
解得
由能量守恒定律有
解得
由于 ,故假设不成
立, 与未达到共速时即滑离 ,不能发生第3次碰撞
所以与碰撞2次,与 分离.
同课章节目录
