江西省赣州市信丰县2024-2025学年八年级上学期第三阶段检测数学试题(A卷)(无答案)
文档属性
| 名称 | 江西省赣州市信丰县2024-2025学年八年级上学期第三阶段检测数学试题(A卷)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 354.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 11:32:15 | ||
图片预览


文档简介
八年级数学第二次学情调研试卷A卷
一、选择题:(本大题6小题,每小题3分,共18分)
1.下列式子中,运算正确的是( )
A. B. C. D.
2. 下列因式分解结果正确的是( )
A. x2+3x+2=x(x+3)+2 B. 4x2﹣9=(4x+3)(4x﹣3)
C. x2﹣5x+6=(x﹣2)(x﹣3) D. a2﹣2a+1=(a+1)2
3.如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
A.2 B.4 C.6 D.8
(3) (5)
4.游戏时,3名同学分别站在三个顶点的位置上、要求在他们中间放一个凳子,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置是在△ABC的( )
A.三边垂直平分线的交点 B.三条角平分线的交点
C.三边中线的交点 D.三边上高的交点
5.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
A.(0,3) B.(0,2) C.(0,1) D.(0,0)
6.我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(n=1,2,3,4,…)的展开式的系数规律(按a的次数由大到小的顺序):
请根据上述规律,则展开式中含项的系数是( )
A.2021 B.2022 C.2023 D.2024
二、填空题(本题共6小题,每小题3分,共18分)
7.因式分解:
8.若,.则
9.某市在旧城改造中计划在一块如图所示的三角形空地上种植某种草皮以美化环境,AB=20m,AC=30m.已知这种草皮每平方米a元,则购买这种草皮至少需要 元.
10. 已知a2+a﹣1=0,a3+2a2+2020 =________
11.已知a、b、c是△ABC的三边的长,且满足a2+2b2+c2﹣2b(a+c)=0,则此三角形的形状为 .
12. 在多项式中添加一个单项式,使其成为一个完全平方式,则添加的单项式为______________
三、(本大题共5题,每题6分,共30分),
13. 计算:(1)已知,.求的值;
(2)
14.阅读下列材料:
在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”,
下面是小涵同学用换元法对多项式(x -9)(x +1)+25 进行因式分解的过程.解;设x =y
原式=(y-9)(y+1)+25(第一步)
=(第二步)
=(第三步)
=(第四步)
请根据上述材料回答下列问题:
(1)小涵同学的解法中,第二步到第三步运用了因式分解的 __________;
A.提取公因式法B.平方差公式法C.完全平方公式法
(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:__________
(3)请你用换元法对多项式(9x -6x+3)(9x -6x-1)+4进行因式分解.
15.先化简,再求值:[(x+2y)(x﹣2y)﹣(x﹣4y)2]÷4y,其中x=5,y=2.
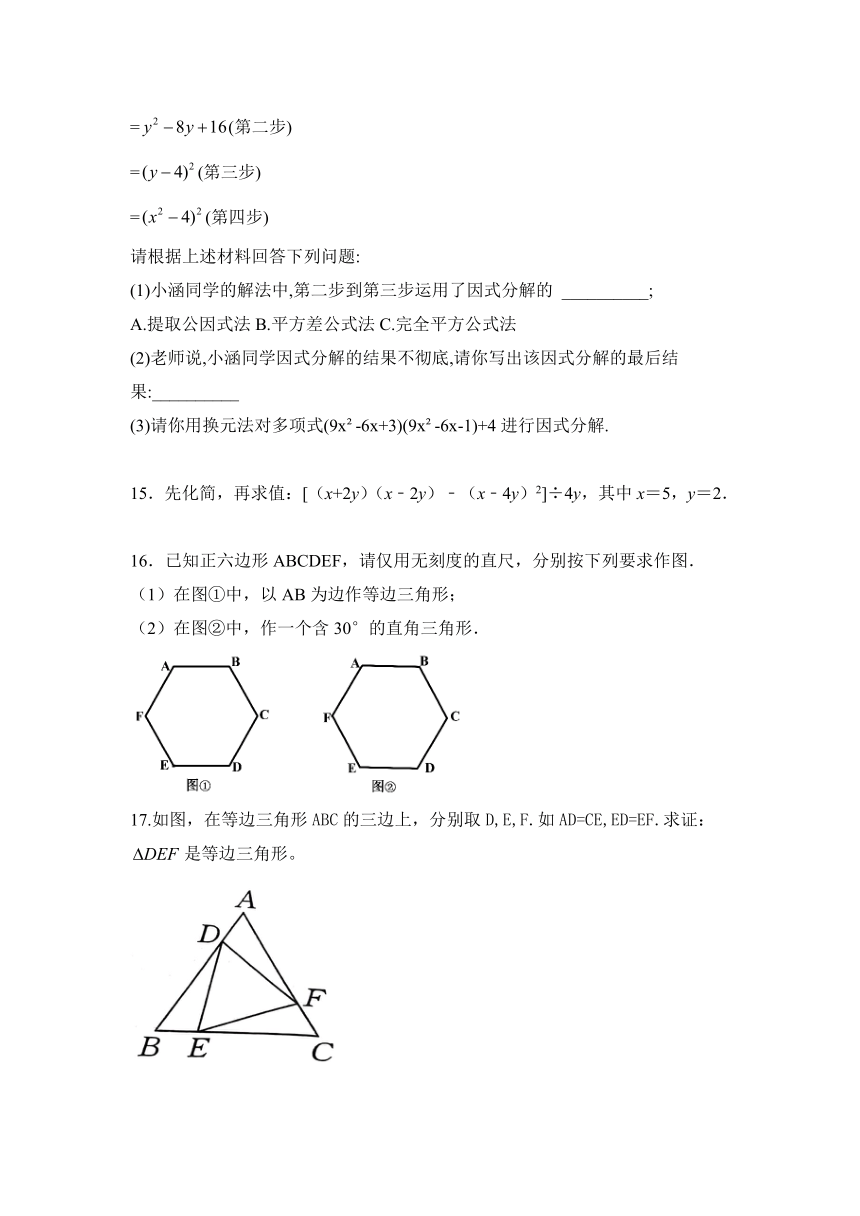
16.已知正六边形ABCDEF,请仅用无刻度的直尺,分别按下列要求作图.
(1)在图①中,以AB为边作等边三角形;
(2)在图②中,作一个含30°的直角三角形.
17.如图,在等边三角形ABC的三边上,分别取D,E,F.如AD=CE,ED=EF.求证:是等边三角形。
四、(本大题共3小题,每题8分,共24分)
18. 在数学中,通常可以运用一些公式来解决问题.比如,运用两数和的完全平方公式(a+b)2=a2+2ab+b2,能够在三个代数式a+b,ab,a2+b2中,当已知其中任意两个代数式的值时,求出第三个代数式的值.例如:已知a+b=3,ab=2,求a2+b2的值.
解:将a+b=3两边同时平方,得(a+b)2=32,
即a2+2ab+b2=9, 因为ab=2,
等量代换,得a2+b2+2×2=9, 所以a2+b2=5.
请根据以上信息,解答下列问题.
(1)已知a﹣b=1,a2+b2=17,求ab的值.
(2)如图,已知两个正方形的边长分别为a、b,若a+b=7,ab=9,求图中阴影部分的面积.
(3)若(2025﹣x)(x﹣2024)=﹣6,则(2025﹣x)2+(x﹣2024)2的值为 .
19. 如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,连接BE.
(1)求证:AD=BE;
(2)若∠CAE=15°,AD=4,求AB的长.
20.【定义】配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和,这种方法称之为配方法,例如:可将多项式通过横档变形化为的形式,这个变形过程中应用了配方法.
(1)【理解】对于多项式,当x=____________时,它的最小值为______________.
(2)【应用】若,求的值.
(3)【拓展】是的三边,且有.若c为整数,求c的值.
五、(本大题共2小题,每题9分,共18分)
21.对数的定义:一般地,若,那么叫做以为底N的对数,记作.例如:其中的对数叫做常用对数,此时可记为.
(1)解方程:
(2)求证:
(3)计算:
22. 课本再现
我们知道,角平分线上的点到角的两边的距离相等.同时,角的内部到角的两边距离相等的点在角的平分线上. (1)如图1,已知BG,CG是△ABC的角平分线,求证:点G到三边AB,BC,AC的距离相等;
(2)如图2,BP,CP分别是△ABC的一个内角及一个外角的平分线,PQ⊥AC,连接AP.若。∠BAC=60°,求∠PAC的度数;
六.解答题(12分)
23.已知△ABC为等边三角形,点D,E分别在边AB,BC上,且AD=BE,AE,CD相交于点F.
(1)在图1中,全等三角形有____对,请选择其中一对全等三角形进行证明;
(2)如图2,过点C作CG⊥AE,垂足为点G,求证:CF=2FG; (3)如图3,若点H在线段CF上,且AF=FH,连接BH交EF于点M,连接CM,试判断FM与FC之间的数量关系,并说明理由.
一、选择题:(本大题6小题,每小题3分,共18分)
1.下列式子中,运算正确的是( )
A. B. C. D.
2. 下列因式分解结果正确的是( )
A. x2+3x+2=x(x+3)+2 B. 4x2﹣9=(4x+3)(4x﹣3)
C. x2﹣5x+6=(x﹣2)(x﹣3) D. a2﹣2a+1=(a+1)2
3.如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
A.2 B.4 C.6 D.8
(3) (5)
4.游戏时,3名同学分别站在三个顶点的位置上、要求在他们中间放一个凳子,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置是在△ABC的( )
A.三边垂直平分线的交点 B.三条角平分线的交点
C.三边中线的交点 D.三边上高的交点
5.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
A.(0,3) B.(0,2) C.(0,1) D.(0,0)
6.我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(n=1,2,3,4,…)的展开式的系数规律(按a的次数由大到小的顺序):
请根据上述规律,则展开式中含项的系数是( )
A.2021 B.2022 C.2023 D.2024
二、填空题(本题共6小题,每小题3分,共18分)
7.因式分解:
8.若,.则
9.某市在旧城改造中计划在一块如图所示的三角形空地上种植某种草皮以美化环境,AB=20m,AC=30m.已知这种草皮每平方米a元,则购买这种草皮至少需要 元.
10. 已知a2+a﹣1=0,a3+2a2+2020 =________
11.已知a、b、c是△ABC的三边的长,且满足a2+2b2+c2﹣2b(a+c)=0,则此三角形的形状为 .
12. 在多项式中添加一个单项式,使其成为一个完全平方式,则添加的单项式为______________
三、(本大题共5题,每题6分,共30分),
13. 计算:(1)已知,.求的值;
(2)
14.阅读下列材料:
在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”,
下面是小涵同学用换元法对多项式(x -9)(x +1)+25 进行因式分解的过程.解;设x =y
原式=(y-9)(y+1)+25(第一步)
=(第二步)
=(第三步)
=(第四步)
请根据上述材料回答下列问题:
(1)小涵同学的解法中,第二步到第三步运用了因式分解的 __________;
A.提取公因式法B.平方差公式法C.完全平方公式法
(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:__________
(3)请你用换元法对多项式(9x -6x+3)(9x -6x-1)+4进行因式分解.
15.先化简,再求值:[(x+2y)(x﹣2y)﹣(x﹣4y)2]÷4y,其中x=5,y=2.
16.已知正六边形ABCDEF,请仅用无刻度的直尺,分别按下列要求作图.
(1)在图①中,以AB为边作等边三角形;
(2)在图②中,作一个含30°的直角三角形.
17.如图,在等边三角形ABC的三边上,分别取D,E,F.如AD=CE,ED=EF.求证:是等边三角形。
四、(本大题共3小题,每题8分,共24分)
18. 在数学中,通常可以运用一些公式来解决问题.比如,运用两数和的完全平方公式(a+b)2=a2+2ab+b2,能够在三个代数式a+b,ab,a2+b2中,当已知其中任意两个代数式的值时,求出第三个代数式的值.例如:已知a+b=3,ab=2,求a2+b2的值.
解:将a+b=3两边同时平方,得(a+b)2=32,
即a2+2ab+b2=9, 因为ab=2,
等量代换,得a2+b2+2×2=9, 所以a2+b2=5.
请根据以上信息,解答下列问题.
(1)已知a﹣b=1,a2+b2=17,求ab的值.
(2)如图,已知两个正方形的边长分别为a、b,若a+b=7,ab=9,求图中阴影部分的面积.
(3)若(2025﹣x)(x﹣2024)=﹣6,则(2025﹣x)2+(x﹣2024)2的值为 .
19. 如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,连接BE.
(1)求证:AD=BE;
(2)若∠CAE=15°,AD=4,求AB的长.
20.【定义】配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和,这种方法称之为配方法,例如:可将多项式通过横档变形化为的形式,这个变形过程中应用了配方法.
(1)【理解】对于多项式,当x=____________时,它的最小值为______________.
(2)【应用】若,求的值.
(3)【拓展】是的三边,且有.若c为整数,求c的值.
五、(本大题共2小题,每题9分,共18分)
21.对数的定义:一般地,若,那么叫做以为底N的对数,记作.例如:其中的对数叫做常用对数,此时可记为.
(1)解方程:
(2)求证:
(3)计算:
22. 课本再现
我们知道,角平分线上的点到角的两边的距离相等.同时,角的内部到角的两边距离相等的点在角的平分线上. (1)如图1,已知BG,CG是△ABC的角平分线,求证:点G到三边AB,BC,AC的距离相等;
(2)如图2,BP,CP分别是△ABC的一个内角及一个外角的平分线,PQ⊥AC,连接AP.若。∠BAC=60°,求∠PAC的度数;
六.解答题(12分)
23.已知△ABC为等边三角形,点D,E分别在边AB,BC上,且AD=BE,AE,CD相交于点F.
(1)在图1中,全等三角形有____对,请选择其中一对全等三角形进行证明;
(2)如图2,过点C作CG⊥AE,垂足为点G,求证:CF=2FG; (3)如图3,若点H在线段CF上,且AF=FH,连接BH交EF于点M,连接CM,试判断FM与FC之间的数量关系,并说明理由.
同课章节目录
