2025年中考数学复习--梯形的存在性问题(含解析)
文档属性
| 名称 | 2025年中考数学复习--梯形的存在性问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 841.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-30 19:22:46 | ||
图片预览




文档简介
梯形的存在性问题
1.如图1,抛物线 交x轴于点A(1,0)和点B,交y轴于点C(0,3).
(1) 求抛物线解析式;
(2) 在抛物线上找出点 P,使PC=PO,求点 P 的坐标;
(3)将直线AC沿x轴的正方向平移,平移后的直线交y轴于点M,交抛物线于点N.当四边形ACMN 为等腰梯形时,求点 M、N 的坐标.
2如图1,AD∥BC,∠ABC=90°,AD=3,AB=4,点P为射线BC上一动点,以P 为圆心,BP 长为半径作⊙P,交射线 BC 于点Q,联结BD、AQ 相交于点G,⊙P 与线段BD、AQ 分别相交于点E、F.
(1) 如果BE=FQ,求⊙P 的半径;
(2)设BP=x,FQ=y,求y关于x的函数关系式,并写出x的取值范围;
(3) 联结PE、PF,如果四边形 EGFP 是梯形,求 BE 的长.
3.如图1,在平面直角坐标系中,抛物线 经过点A(-2,0)和原点,点B 在抛物线上且 抛物线的对称轴与x轴相交于点 P.
(1) 求抛物线的解析式,并直接写出点 P 的坐标;
(2)点C 为抛物线上一点,若四边形 AOBC 为等腰梯形且AO∥BC,求点C 的坐标;
(3)点D 在AB上,若△ADP 与△ABO相似,求点 D 的坐标.
4.如图1,已知在 Rt△ABC中,∠ACB=90°,AC=6,BC=8,点F 在线段AB上,以点B 为圆心,BF 为半径的圆交BC 于点E,射线AE 交圆B 于点D(点 D、E 不重合).
(1)如果BF=x,EF=y,求y与x之间的函数关系式,并写出它的定义域;
(2) 如果 求ED 的长;
(3) 联结CD、BD,请判断四边形ABDC 是否为直角梯形 说明理由.
5.在圆O中,C是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D,联结AO、BO、AD、BD.已知圆O的半径长为5,弦AB 的长为8.
(1) 如图1,当点 D 是弧AB 的中点时,求CD 的长;
(2)如图2,设 求y关于x 的函数解析式并写出定义域;
(3) 若四边形 AOBD 是梯形,求AD 的长.
6.如图1,已知在 Rt△ABC中,∠ACB=90°,AC=6,BC=8,点F 在线段AB上,以点B 为圆心,BF 为半径的圆交BC 于点E,射线AE 交圆B 于点D(点 D、E 不重合).
(1)如果BF=x,EF=y,求y与x之间的函数关系式,并写出它的定义域;
(2) 如果 求ED的长;
(3)联结CD、BD,请判断四边形ABDC 是否为直角梯形 说明理由.
专题直击
(3) 联结CD、BD,请判断四边形ABDC 是否为直角梯形 说明理由.
7.如图,四边形ABCD 是直角梯形, 点P 从点A 出发以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B 运动,其中一个动点到达终点时,另一个点也随之停止运动.从运动开始,经过多少时间,四边形 PQCD 成为平行四边形 成为等腰梯形
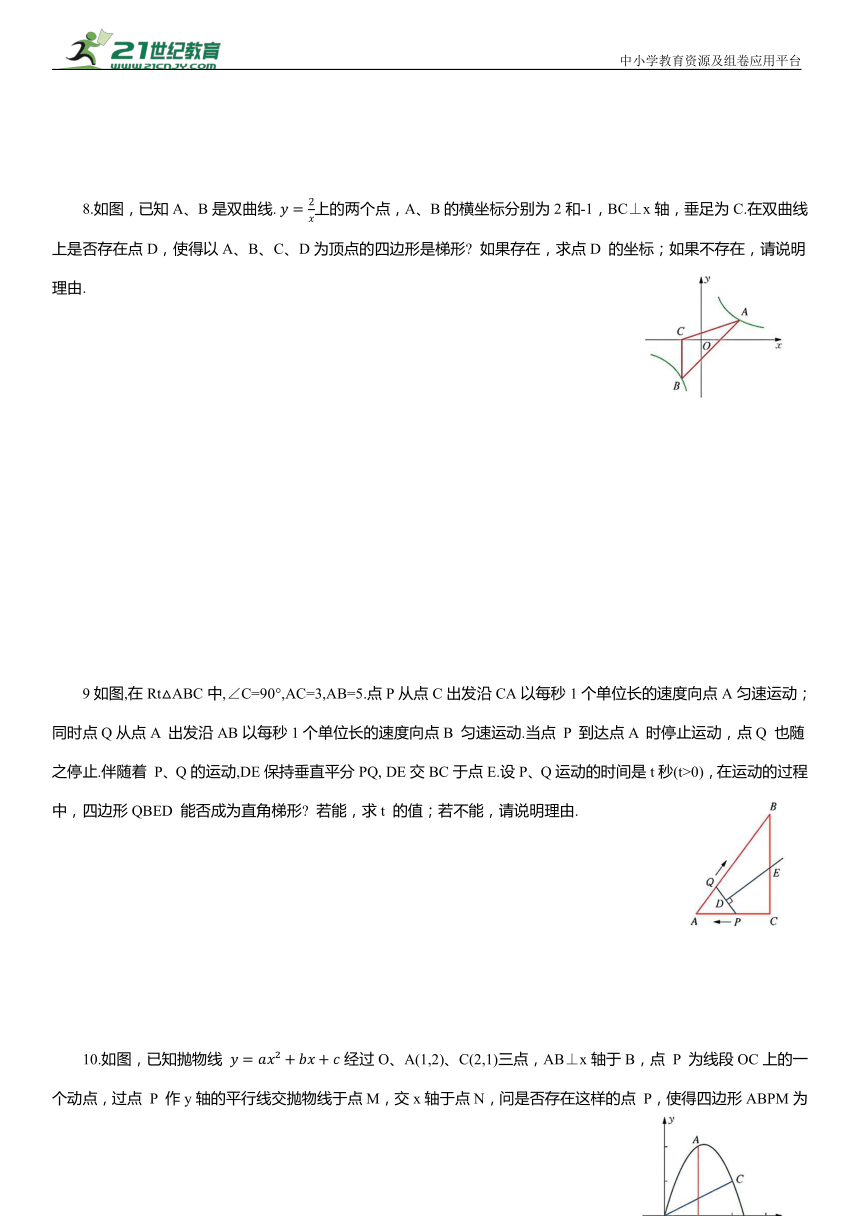
8.如图,已知A、B是双曲线. 上的两个点,A、B的横坐标分别为2和-1,BC⊥x轴,垂足为C.在双曲线上是否存在点D,使得以A、B、C、D为顶点的四边形是梯形 如果存在,求点D 的坐标;如果不存在,请说明理由.
9如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;同时点Q从点A 出发沿AB以每秒1个单位长的速度向点B 匀速运动.当点 P 到达点A 时停止运动,点Q 也随之停止.伴随着 P、Q的运动,DE保持垂直平分PQ, DE交BC于点E.设P、Q运动的时间是t秒(t>0),在运动的过程中,四边形QBED 能否成为直角梯形 若能,求t 的值;若不能,请说明理由.
10.如图,已知抛物线 经过O、A(1,2)、C(2,1)三点,AB⊥x轴于B,点 P 为线段OC上的一个动点,过点 P 作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点 P,使得四边形ABPM为等腰梯形 若存在,求出此时点P的坐标;若不存在,请说明理由.
11如图1,已知直线 与x轴、y轴分别相交于点A、B,点C的坐标为(2,0).
(1) 求△ABC 的面积;
(2)点D 在y轴上,若A、B、C、D四点为梯形的四个顶点,求所有满足条件的点 D 的坐标.
12如图1,在直角坐标平面内,直线 与x轴、y轴分别交于点 A、B,点C在x轴正半轴上,且满足
(1) 求线段AB 的长及点C 的坐标;
(2)设线段 BC 的中点为E,如果梯形 AECD 的顶点 D 在y轴上,CE 是底边,求点 D 的坐标和梯形AECD 的面积.
13.如图1,在平面直角坐标系中,已知一次函数的图像经过点 A(0,4)、B(2,0).
(1) 求这个一次函数的解析式;
(2)把直线AB 向下平移,若平移后的直线与x轴、y轴分别相交于点C、D,且AC=BC,如果点E在直线CD上,四边形ABDE是等腰梯形,求点E 的坐标.
14.如图1,在平面直角坐标系中,直线y= kx+8分别与x轴、y轴交于点A、B,点A 的坐标是(4,0), C是AB的中点.
(1) 求k 的值;
(2) 如果以B、C、O、D为顶点的四边形是菱形,请直接写出点 D 的坐标;
(3)在(2)的条件下,在直线OD 上是否存在点E,使得以点A、O、E、B 为顶点的四边形是等腰梯形,如果存在,求出点 E 的坐标;如果不存在,请说明理由.
15. 梯形的存在性问题
如图1,已知一次函数y=-x+7与正比例函数 的图像交于点A,且与x轴交于点B.
(1) 求点 A 和点B 的坐标;
(2) 过点A 作AC⊥y轴于点C,动点 P从点O出发,以每秒1个单位长度的速度,沿O-C-A的路线向点A 运动;点R从点B 出发,以相同速度向点O运动,在运动过程中,过点 R 作直线l⊥x轴,交线段BA 或线段AO于点Q.当点 P 到达点A 时,点P 和点R 都停止运动.在运动过程中,设动点 P 运动的时间为t 秒(t>0).
① 当t 为何值时,以A、P、R为顶点的三角形的面积为8
②在①的条件下,是否存在以A、P、Q、M为顶点的四边形是等腰梯形 若存在,请直接写出点 M 的坐标;若不存在,请说明理由.
16.如图1,在Rt△OBP中,∠OBP=90°,OB=8,PB=6,BC为斜边OP 上的中线,边OP 绕着点O逆时针方向旋转至 ,过点 P 作PA⊥OP'于点A,连结AC 并延长交边OB 于点D.
(1)求AC的长;
(2)设AP=x,S四边形ACBP =y,,求y关于x 的函数解析式,并写出定义域;
(3) 当四边形 ACBP 是梯形时,求AP 的长.
1.满分解答
(1) 将点A(1,0)、C(0, 3)分别代入 得 解得
所以抛物线的解析式为
(2)如图2,由 PO=PC,得点 P 在OC 的垂直平分线上.所以
解方程 得 所以 或
(3)如图3,延长 NA 交y轴于点G.设G(0, m).
如果四边形ACMN 是等腰梯形,那么GM=GN,GC=GA.
由 得 解得
所以G(o, )..所以
如图4,作 NH ⊥y轴于H,那么
设N(n,n -4n+3),那么
由 得3GH=4NH.
所以 整理,得
解得 (与点 A 重合,舍去), 所以
在Rt△GNH 中, 所以
所以 所以
考点伸展
第(3)题的后半部分也可以这样做:
在Rt△GNH 中,设NH=3n,GH=4n,那么(
所以 将点 N 代入. 得
整理,得 因式分解,得
所以 或3n=1(点 N 与点A 重合,舍去).
2.满分解答
(1)如图2,如果BE=FQ,那么等腰三角形 PBE≌等腰三角形 PQF.
所以∠GBQ=∠GQB.所以GB=GQ.
所以点G在BQ 的垂直平分线上.所以G是AQ 的中点.
因为AD∥BC,BQ=AD=3.
所以⊙P 的半径等于
(2) 如图3,作PH⊥QF 于H,那么
在Rt△ABQ中,AB=4, BQ=2x,所以,
所以
在Rt△PHQ中,
所以 整理,得 定义域是
(3)①如图4(局部图),当PE∥FG时,由PB=PE,得QB=QG=2x.由AD ∥BQ,得AG=AD=3.
由AQ=AG+QG,列方程 解得
此时在等腰三角形 PBE 中,
②如图5(局部图),当PF ∥EG时,由PQ=PF,得BG=BQ=2x.
由AD ∥BQ,得DG=DA =3.
由BD=BG+DG,列方程5=3+2x.解得x=1.
此时在等腰三角形 PBE 中,
考点伸展
第(2)题定义域中 的几何意义是点E与点D重合时,点P 在BD 的垂直平分线上.
如图5,由AD=3,AB=4,得BD=5.
所以
由 得 解得
3.满分解答
(1)因为抛物线 与x轴交于点A(-2,0)和原点,所以
抛物线的对称轴是直线x=-1,点P 的坐标为(--1,0).
(2) 如图2,作 BH⊥x轴于H.设点 B 的坐标为
由 得AH=2BH.所以(
解得x=2,或x=-2(B、A重合,舍去).所以B(2,2).
若四边形AOBC 为等腰梯形且AO∥BC,那么B、C关于抛物线的对称轴x=-1对称.所以点C 的坐标为(-4,2).
(3)如图3,作DE⊥x轴于E.
在Rt△ADE 中,已知 所以
由于△ADP 与△ABO有公共角∠A,分两种情况讨论相似:
①如图4,当 时, 所以
此时DE=1, AE=2.所以点 D 的坐标为(0, 1).
②如图5,当 时, 所以
此时 所以 所以点 D 的坐标为
考点伸展
如果第(2)题改为以A、O、B、C为顶点的四边形是等腰梯形,那么就要分三种情况:△AOB的三边的垂直平分线都可以是等腰梯形的对称轴.
第二种情况:如图6,如果OC∥AB,那么点C与点O关于直线AB 的垂直平分线对称.
点C在直线 上,设C(2m,m).
由CB=OA=2,得( 所以(
解得 或m=2(此时四边形AOCB 是平行四边形).所以(
第三种情况:如图7,如果AC∥OB,那么点C 与点A 关于直线OB 的垂直平分线对称.
点C在直线y=x+2上,设C(n,n+2).
由CB=AO=2,得( 所以(
解得n=2,或n=0(舍去).所以C(2,4).
4.满分解答
(1)在Rt△ABC中,AC=6,BC=8,所以AB=10, sin∠ABC=
如图2,作EH⊥AB 于H.
在Rt△EBH 中,BE=BF=x,所以
在Rt△EFH 中,
所以EH=3FH.
所以 定义域是0(2)如图3,如果 那么∠EBD=2∠ABC.
作∠EBD 的平分线交DE 于G,那么 BG 垂直平分DE.
设EG=DG=3m,BG=4m,BE=5m.
由tan∠AEC=tan∠BEG,得 所以
解得 所以
(3)如图4,当∠ABD=90°时,等腰三角形BDE 的顶角是确定的.
作DM⊥BC 于M.设BD=BE=5m,那么BM=3m,DM=4m.
所以EM=2m.
由由 tan∠AEC=tan∠DEM,得 所以
解得m=1.所以BD=5m=5.
而直角三角形 ABC 斜边上的高
因为CN≠DB,所以CD与AB 不平行.所以四边形ABCD 不能为直角梯形.
考点伸展
第(3)题也可以先假设四边形 ABDC 是直角梯形,如图4所示.
一方面,在 Rt△BCD 中, 所以
另一方面,由CD∥AB,得
所以
因为 所以假设矛盾.
5.满分解答
(1)如图3,当点D 是弧AB 的中点时,OD 垂直平分弦AB,垂足为C.在Rt△OAC中,OA=5,AC=4,所以OC=3.此时CD=OD-OC=5-3=2.
(2)如图5,△ACO和△OBD 都可以与△OBC 相关联.
第一步,用x表示OC 的长.
如图4,作OH⊥AB于H,那么OH=3,CH=4-x,所以
第二步,如图5,因为 所以
定义域是0(3)如图6,延长BO交圆于点E,那么BE 是圆的直径,AE=2OH=6.
情形1,如图6,如果OA∥BD,那么∠DBA=∠BAO=∠ABO.
根据相等的圆周角所对的弧相等,相等的弧所对的弦相等,此时AD=AE=6.
情形2,如图7,如果AD ∥BO,那么四边形ADBE 是等腰梯形.
作AM⊥BE于M,作DN⊥BE 于N,那么AD=MN.
在 Rt△AEM 中, 所以
此时
考点伸展
第(2)题也可以用面积公式求△ACO的面积,用割补法求△OBD 的面积.
中小学教育资源及组卷应用平台
如图8,△OBC 和△DBC的公共底边为BC,高OH=3,求高DG也要先用x表示OC的长,再根据相似比求得 DG 的长.
6.满分解答
(1)在Rt△ABC中,AC=6, BC=8,所以.
如图2,作EH⊥AB 于H.
在Rt△EBH 中,BE=BF=x,所以
在Rt△EFH 中,.
所以EH=3FH.
所以 定义域是0(2) 如图3,如果 那么∠EBD=2∠ABC.
作∠EBD的平分线交DE 于G,那么BG 垂直平分DE.
设EG=DG=3m,BG=4m,BE=5m.
由tan∠AEC=tan∠BEG,得 所以
解得 所以
(3)如图4,当∠ABD=90°时,等腰三角形 BDE 的顶角是确定的.
作DM⊥BC于M.设BD=BE=5m,那么BM=3m,DM=4m.
所以EM=2m.
由由tan∠AEC=tan∠DEM,得 所以
解得m=1.所以BD=5m=5.
而直角三角形 ABC 斜边上的高
因为CN≠DB,所以CD与AB 不平行.所以四边形ABCD 不能为直角梯形.
考点伸展
第(3)题也可以先假设四边形 ABDC 是直角梯形,如图4所示.
一方面,在 Rt△BCD 中, 所以
另一方面,由CD∥AB,得
所以
因为 所以假设矛盾.
7.满分解答
如图1,如果四边形 PQCD 是平行四边形,那么PD=QC.
所以24-t=3t.解得t=6.
如图2,如果四边形 PQCD 是等腰梯形,作PM⊥BC, DN⊥BC,垂足分别为 M、N,那么QM=CN.
所以t-(28-3t)=4.解得t=8.
8.满分解答
已知A(2,1),B(-1,-2),C(-1,0).设D(x, )
① 如图1,过点 A 作BC的平行线,不存在点 D.
②如图2,当BD ∥AC时,∠ACE=∠DBF,所以
解方程得x=-1或x=6.此时.
③如图3,当CD∥AB时,∠ABE=∠DCF,所以
解方程 得x=1或x=-2.此时D(1,2)或(-2,-1).
9满分解答
①如图1,当 DE ∥QB 时,∠AQP =90°.
在Rt△AQP 中, 所以 解得
②如图2,当DE ∥BC 时,
在 Rt△AQP 中, 所以 解得
10.满分解答
易得抛物线的解析式为 直线OC 的解析式为
设
如图1,作ME⊥AB 于E,作 PF⊥AB 于F.
如果四边形ABPM 为等腰梯形,那么AE=BF.所以.
解方程 整理,得
解得 或x=2(P、C重合,舍去).
所以点 P 的坐标为 (如图2所示).
11满分解答
(1)由 当x=0时,y=1.
所以B(0,1),OB=1.
解方程 得x=-3.
所以A(-3,0),OA=3.
由A(-3,0)、C(2,0),得AC=5.
所以
(2) 第一种情况,过点A 作BC 的平行线交y轴于点D.
由 B(0,1)、C(2,0),得直线 BC 的解析式为
设直线 AD 的解析式为 代入点A(-3,0),得
解得 所以点 D 的坐标为(
第二种情况,过点C 作AB 的平行线交y轴于点D.
由直线 AB 的解析式为 设直线CD 的解析式为
代入点C(2,0),得 解得 所以点D 的坐标为
12满分解答
(1)由 得A(-3,0), B(0,-4).所以 因为 所以OC=2.所以C(2,0).
(2)由B(0, - 4)、C(2,0),得直线 BC 的解析式为y=2x-4.
因为四边形 AECD 为梯形,所以 AD ∥BC.所以kAD=kBC=2.
设直线AD 的解析式为y=2x+b,代入A(-3,0),得-6+b=0.解得b=6.
所以直线AD 的解析式为y=2x+6, D(0,6).
所以
因为点 E 为线段BC 的中点,所以
所以
13.满分解答
(1)设y= kx+4,代入B(2,0),得2k+4=0,解得k=-2.所以y=-2x+4.
(2)如图2,设C(a,0),已知A(0,4), B(2,0),AC=BC,所以
所以 解得a=-3.所以C(-3,0).
设CD 的解析式为y=-2x+b,代入C(-3,0),得6+b=0.解得b=-6.
所以y=-2x-6,D(0,-6).
因为四边形ABDE 是等腰梯形,可知AB∥ED.设E(m,-2m-6).
【方法一】由腰AE=BD,根据 列方程.
因为A(0,4)、B(2,0)、D(0,-6),所以
解得 (此时ABDE 是平行四边形,舍去).所以E(-6,6).
【方法二】由对角线AD=BE,根据 列方程.
因为A(0,4)、B(2,0)、D(0,-6),所以(
解得 (此时点 E 在点D 右侧,ABED 是平行四边形,舍去).
所以E(-6,6).
【方法三】由 HE=HD,根据 列方程.
因为A(0,4)、B(2,0)、D(0, - 6),所以 H(1,2).
所以
解得 (此时点 E 与点D 重合,舍去).
所以E(-6,6).
【方法四】由CA=CB,根据 列方程.
因为E(m,-2m-6)、D(0,-6),所以
所以
解得m=-6.所以E(-6,6).
14.满分解答
(1)将点A(4,0)代入y= kx+8,得4k+8=0.解得k=-2.
(2)如图2,因为点C是AB 的中点,所以点C的坐标为(2,4).
因为OC 是直角三角形AOB 斜边上的中线,所以CB=CO.
因此CB、CO 是菱形的邻边,BO为菱形的对角线.
所以D、C两点关于y轴对称,点 D 的坐标是(-2,4).
(3)由O、D(-2,4),可得直线OD 的解析式为y=-2x.
所以OD ∥AB.
因为A、O、B三点是确定的,过△AOB 的每个顶点画对边的平行线,与直线OD 交于点E.
①如图3,过点 A 画OB 的平行线,四边形 BOEA 是平行四边形.
②如图4,过点 B 画OA 的平行线,四边形EOAB 是平行四边形.
③如图5,因为OD ∥AB,如果BE=AO,那么四边形BEOA是等腰梯形.
设点E 的坐标为(x,-2x).由 得
整理,得
因式分解,得(x+4)(5x+12)=0.
所以x=-4,或
当x=-4时,点E的坐标为(-4,8),此时EB∥x轴,四边形BEOA 是平行四边形.
当 时,点E的坐标为
15满分解答
(1) 联立y=-x+7和 解得x=3,y=4.所以A(3,4).
解方程-x+7=0,得x=7.所以B(7,0).
(2)①(i)如图2,当点P在OC上时,OP=BR=t,CP=4-t,OR=7-t.
所以
整理 解得t=2,或t =6(点 P 不在OC 上,舍去).
(ii)如图3,当点P 在CA上时,PA≤3,PA对应的高为4,所以△APR的面积小于等于6.
② 在①的条件下,A(3,4)、P(0,2)、Q(5,2).所以PQ∥x轴.
分三种情况讨论等腰梯形:
(i) 如图4,对称轴是 PQ 的垂直平分线,AM ∥PQ.
此时点A(3,4)关于直线 对称的点 M 的坐标为(2,4).
(ii)如图5,对称轴是AQ 的垂直平分线,PM∥AQ.
因为AE=QE,所以设PF=MF=m,那么M(m,2-m).
由对角线AM=PQ=5,得. 所以(
整理,得 解得m=3,或m=-2.
当m=3时,M(3,-1).
当m=-2时,四边形MPQA 是平行四边形,图中点M'对应的位置.
(iii)如图6,对称轴是AP 的垂直平分线,QM∥AP.
因为AE:PE=2:3,所以设M(5-3m,2-2m).
由腰 得 所以
整理,得 解得 或m=1.
当 时,
当m=1时,四边形 PMQA 是平行四边形,图中点. 对应的位置.
16.满分解答
(1) 如图2,在Rt△OBP 中,OB=8,PB=6,所以OP =10.
因为AC是Rt△AOP 的斜边OP 上的中线,所以
(2) 如图2,因为C是OP 的中点,所以
在Rt△AOP 中,AP=x,OP =10,所以,
所以
又因为S△BOP =24,所以
定义域是0(3)①如图3,当AC ∥PB时,延长AC交OB 于D,那么CD是△OBP 的中位线.
作 PE⊥AC于E,那么△PEC≌△ODC.
所以CE=CD=3,PE=OD=4.
在Rt△AEP 中,AE=5-3=2, PE=4,所以.
②如图4,当AP∥CB时,作CD⊥OB于D,作AH⊥OB 于H,作PF⊥AH于F.
由 设AF=3m,PF=4m,那么AP=5m.
在Rt△AOH 中,AH=6+3m,OH=8-4m,所以(
在Rt△AOP 中,
所以
解得 或m=0(舍去).
此时
1.如图1,抛物线 交x轴于点A(1,0)和点B,交y轴于点C(0,3).
(1) 求抛物线解析式;
(2) 在抛物线上找出点 P,使PC=PO,求点 P 的坐标;
(3)将直线AC沿x轴的正方向平移,平移后的直线交y轴于点M,交抛物线于点N.当四边形ACMN 为等腰梯形时,求点 M、N 的坐标.
2如图1,AD∥BC,∠ABC=90°,AD=3,AB=4,点P为射线BC上一动点,以P 为圆心,BP 长为半径作⊙P,交射线 BC 于点Q,联结BD、AQ 相交于点G,⊙P 与线段BD、AQ 分别相交于点E、F.
(1) 如果BE=FQ,求⊙P 的半径;
(2)设BP=x,FQ=y,求y关于x的函数关系式,并写出x的取值范围;
(3) 联结PE、PF,如果四边形 EGFP 是梯形,求 BE 的长.
3.如图1,在平面直角坐标系中,抛物线 经过点A(-2,0)和原点,点B 在抛物线上且 抛物线的对称轴与x轴相交于点 P.
(1) 求抛物线的解析式,并直接写出点 P 的坐标;
(2)点C 为抛物线上一点,若四边形 AOBC 为等腰梯形且AO∥BC,求点C 的坐标;
(3)点D 在AB上,若△ADP 与△ABO相似,求点 D 的坐标.
4.如图1,已知在 Rt△ABC中,∠ACB=90°,AC=6,BC=8,点F 在线段AB上,以点B 为圆心,BF 为半径的圆交BC 于点E,射线AE 交圆B 于点D(点 D、E 不重合).
(1)如果BF=x,EF=y,求y与x之间的函数关系式,并写出它的定义域;
(2) 如果 求ED 的长;
(3) 联结CD、BD,请判断四边形ABDC 是否为直角梯形 说明理由.
5.在圆O中,C是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D,联结AO、BO、AD、BD.已知圆O的半径长为5,弦AB 的长为8.
(1) 如图1,当点 D 是弧AB 的中点时,求CD 的长;
(2)如图2,设 求y关于x 的函数解析式并写出定义域;
(3) 若四边形 AOBD 是梯形,求AD 的长.
6.如图1,已知在 Rt△ABC中,∠ACB=90°,AC=6,BC=8,点F 在线段AB上,以点B 为圆心,BF 为半径的圆交BC 于点E,射线AE 交圆B 于点D(点 D、E 不重合).
(1)如果BF=x,EF=y,求y与x之间的函数关系式,并写出它的定义域;
(2) 如果 求ED的长;
(3)联结CD、BD,请判断四边形ABDC 是否为直角梯形 说明理由.
专题直击
(3) 联结CD、BD,请判断四边形ABDC 是否为直角梯形 说明理由.
7.如图,四边形ABCD 是直角梯形, 点P 从点A 出发以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B 运动,其中一个动点到达终点时,另一个点也随之停止运动.从运动开始,经过多少时间,四边形 PQCD 成为平行四边形 成为等腰梯形
8.如图,已知A、B是双曲线. 上的两个点,A、B的横坐标分别为2和-1,BC⊥x轴,垂足为C.在双曲线上是否存在点D,使得以A、B、C、D为顶点的四边形是梯形 如果存在,求点D 的坐标;如果不存在,请说明理由.
9如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;同时点Q从点A 出发沿AB以每秒1个单位长的速度向点B 匀速运动.当点 P 到达点A 时停止运动,点Q 也随之停止.伴随着 P、Q的运动,DE保持垂直平分PQ, DE交BC于点E.设P、Q运动的时间是t秒(t>0),在运动的过程中,四边形QBED 能否成为直角梯形 若能,求t 的值;若不能,请说明理由.
10.如图,已知抛物线 经过O、A(1,2)、C(2,1)三点,AB⊥x轴于B,点 P 为线段OC上的一个动点,过点 P 作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点 P,使得四边形ABPM为等腰梯形 若存在,求出此时点P的坐标;若不存在,请说明理由.
11如图1,已知直线 与x轴、y轴分别相交于点A、B,点C的坐标为(2,0).
(1) 求△ABC 的面积;
(2)点D 在y轴上,若A、B、C、D四点为梯形的四个顶点,求所有满足条件的点 D 的坐标.
12如图1,在直角坐标平面内,直线 与x轴、y轴分别交于点 A、B,点C在x轴正半轴上,且满足
(1) 求线段AB 的长及点C 的坐标;
(2)设线段 BC 的中点为E,如果梯形 AECD 的顶点 D 在y轴上,CE 是底边,求点 D 的坐标和梯形AECD 的面积.
13.如图1,在平面直角坐标系中,已知一次函数的图像经过点 A(0,4)、B(2,0).
(1) 求这个一次函数的解析式;
(2)把直线AB 向下平移,若平移后的直线与x轴、y轴分别相交于点C、D,且AC=BC,如果点E在直线CD上,四边形ABDE是等腰梯形,求点E 的坐标.
14.如图1,在平面直角坐标系中,直线y= kx+8分别与x轴、y轴交于点A、B,点A 的坐标是(4,0), C是AB的中点.
(1) 求k 的值;
(2) 如果以B、C、O、D为顶点的四边形是菱形,请直接写出点 D 的坐标;
(3)在(2)的条件下,在直线OD 上是否存在点E,使得以点A、O、E、B 为顶点的四边形是等腰梯形,如果存在,求出点 E 的坐标;如果不存在,请说明理由.
15. 梯形的存在性问题
如图1,已知一次函数y=-x+7与正比例函数 的图像交于点A,且与x轴交于点B.
(1) 求点 A 和点B 的坐标;
(2) 过点A 作AC⊥y轴于点C,动点 P从点O出发,以每秒1个单位长度的速度,沿O-C-A的路线向点A 运动;点R从点B 出发,以相同速度向点O运动,在运动过程中,过点 R 作直线l⊥x轴,交线段BA 或线段AO于点Q.当点 P 到达点A 时,点P 和点R 都停止运动.在运动过程中,设动点 P 运动的时间为t 秒(t>0).
① 当t 为何值时,以A、P、R为顶点的三角形的面积为8
②在①的条件下,是否存在以A、P、Q、M为顶点的四边形是等腰梯形 若存在,请直接写出点 M 的坐标;若不存在,请说明理由.
16.如图1,在Rt△OBP中,∠OBP=90°,OB=8,PB=6,BC为斜边OP 上的中线,边OP 绕着点O逆时针方向旋转至 ,过点 P 作PA⊥OP'于点A,连结AC 并延长交边OB 于点D.
(1)求AC的长;
(2)设AP=x,S四边形ACBP =y,,求y关于x 的函数解析式,并写出定义域;
(3) 当四边形 ACBP 是梯形时,求AP 的长.
1.满分解答
(1) 将点A(1,0)、C(0, 3)分别代入 得 解得
所以抛物线的解析式为
(2)如图2,由 PO=PC,得点 P 在OC 的垂直平分线上.所以
解方程 得 所以 或
(3)如图3,延长 NA 交y轴于点G.设G(0, m).
如果四边形ACMN 是等腰梯形,那么GM=GN,GC=GA.
由 得 解得
所以G(o, )..所以
如图4,作 NH ⊥y轴于H,那么
设N(n,n -4n+3),那么
由 得3GH=4NH.
所以 整理,得
解得 (与点 A 重合,舍去), 所以
在Rt△GNH 中, 所以
所以 所以
考点伸展
第(3)题的后半部分也可以这样做:
在Rt△GNH 中,设NH=3n,GH=4n,那么(
所以 将点 N 代入. 得
整理,得 因式分解,得
所以 或3n=1(点 N 与点A 重合,舍去).
2.满分解答
(1)如图2,如果BE=FQ,那么等腰三角形 PBE≌等腰三角形 PQF.
所以∠GBQ=∠GQB.所以GB=GQ.
所以点G在BQ 的垂直平分线上.所以G是AQ 的中点.
因为AD∥BC,BQ=AD=3.
所以⊙P 的半径等于
(2) 如图3,作PH⊥QF 于H,那么
在Rt△ABQ中,AB=4, BQ=2x,所以,
所以
在Rt△PHQ中,
所以 整理,得 定义域是
(3)①如图4(局部图),当PE∥FG时,由PB=PE,得QB=QG=2x.由AD ∥BQ,得AG=AD=3.
由AQ=AG+QG,列方程 解得
此时在等腰三角形 PBE 中,
②如图5(局部图),当PF ∥EG时,由PQ=PF,得BG=BQ=2x.
由AD ∥BQ,得DG=DA =3.
由BD=BG+DG,列方程5=3+2x.解得x=1.
此时在等腰三角形 PBE 中,
考点伸展
第(2)题定义域中 的几何意义是点E与点D重合时,点P 在BD 的垂直平分线上.
如图5,由AD=3,AB=4,得BD=5.
所以
由 得 解得
3.满分解答
(1)因为抛物线 与x轴交于点A(-2,0)和原点,所以
抛物线的对称轴是直线x=-1,点P 的坐标为(--1,0).
(2) 如图2,作 BH⊥x轴于H.设点 B 的坐标为
由 得AH=2BH.所以(
解得x=2,或x=-2(B、A重合,舍去).所以B(2,2).
若四边形AOBC 为等腰梯形且AO∥BC,那么B、C关于抛物线的对称轴x=-1对称.所以点C 的坐标为(-4,2).
(3)如图3,作DE⊥x轴于E.
在Rt△ADE 中,已知 所以
由于△ADP 与△ABO有公共角∠A,分两种情况讨论相似:
①如图4,当 时, 所以
此时DE=1, AE=2.所以点 D 的坐标为(0, 1).
②如图5,当 时, 所以
此时 所以 所以点 D 的坐标为
考点伸展
如果第(2)题改为以A、O、B、C为顶点的四边形是等腰梯形,那么就要分三种情况:△AOB的三边的垂直平分线都可以是等腰梯形的对称轴.
第二种情况:如图6,如果OC∥AB,那么点C与点O关于直线AB 的垂直平分线对称.
点C在直线 上,设C(2m,m).
由CB=OA=2,得( 所以(
解得 或m=2(此时四边形AOCB 是平行四边形).所以(
第三种情况:如图7,如果AC∥OB,那么点C 与点A 关于直线OB 的垂直平分线对称.
点C在直线y=x+2上,设C(n,n+2).
由CB=AO=2,得( 所以(
解得n=2,或n=0(舍去).所以C(2,4).
4.满分解答
(1)在Rt△ABC中,AC=6,BC=8,所以AB=10, sin∠ABC=
如图2,作EH⊥AB 于H.
在Rt△EBH 中,BE=BF=x,所以
在Rt△EFH 中,
所以EH=3FH.
所以 定义域是0
作∠EBD 的平分线交DE 于G,那么 BG 垂直平分DE.
设EG=DG=3m,BG=4m,BE=5m.
由tan∠AEC=tan∠BEG,得 所以
解得 所以
(3)如图4,当∠ABD=90°时,等腰三角形BDE 的顶角是确定的.
作DM⊥BC 于M.设BD=BE=5m,那么BM=3m,DM=4m.
所以EM=2m.
由由 tan∠AEC=tan∠DEM,得 所以
解得m=1.所以BD=5m=5.
而直角三角形 ABC 斜边上的高
因为CN≠DB,所以CD与AB 不平行.所以四边形ABCD 不能为直角梯形.
考点伸展
第(3)题也可以先假设四边形 ABDC 是直角梯形,如图4所示.
一方面,在 Rt△BCD 中, 所以
另一方面,由CD∥AB,得
所以
因为 所以假设矛盾.
5.满分解答
(1)如图3,当点D 是弧AB 的中点时,OD 垂直平分弦AB,垂足为C.在Rt△OAC中,OA=5,AC=4,所以OC=3.此时CD=OD-OC=5-3=2.
(2)如图5,△ACO和△OBD 都可以与△OBC 相关联.
第一步,用x表示OC 的长.
如图4,作OH⊥AB于H,那么OH=3,CH=4-x,所以
第二步,如图5,因为 所以
定义域是0
情形1,如图6,如果OA∥BD,那么∠DBA=∠BAO=∠ABO.
根据相等的圆周角所对的弧相等,相等的弧所对的弦相等,此时AD=AE=6.
情形2,如图7,如果AD ∥BO,那么四边形ADBE 是等腰梯形.
作AM⊥BE于M,作DN⊥BE 于N,那么AD=MN.
在 Rt△AEM 中, 所以
此时
考点伸展
第(2)题也可以用面积公式求△ACO的面积,用割补法求△OBD 的面积.
中小学教育资源及组卷应用平台
如图8,△OBC 和△DBC的公共底边为BC,高OH=3,求高DG也要先用x表示OC的长,再根据相似比求得 DG 的长.
6.满分解答
(1)在Rt△ABC中,AC=6, BC=8,所以.
如图2,作EH⊥AB 于H.
在Rt△EBH 中,BE=BF=x,所以
在Rt△EFH 中,.
所以EH=3FH.
所以 定义域是0
作∠EBD的平分线交DE 于G,那么BG 垂直平分DE.
设EG=DG=3m,BG=4m,BE=5m.
由tan∠AEC=tan∠BEG,得 所以
解得 所以
(3)如图4,当∠ABD=90°时,等腰三角形 BDE 的顶角是确定的.
作DM⊥BC于M.设BD=BE=5m,那么BM=3m,DM=4m.
所以EM=2m.
由由tan∠AEC=tan∠DEM,得 所以
解得m=1.所以BD=5m=5.
而直角三角形 ABC 斜边上的高
因为CN≠DB,所以CD与AB 不平行.所以四边形ABCD 不能为直角梯形.
考点伸展
第(3)题也可以先假设四边形 ABDC 是直角梯形,如图4所示.
一方面,在 Rt△BCD 中, 所以
另一方面,由CD∥AB,得
所以
因为 所以假设矛盾.
7.满分解答
如图1,如果四边形 PQCD 是平行四边形,那么PD=QC.
所以24-t=3t.解得t=6.
如图2,如果四边形 PQCD 是等腰梯形,作PM⊥BC, DN⊥BC,垂足分别为 M、N,那么QM=CN.
所以t-(28-3t)=4.解得t=8.
8.满分解答
已知A(2,1),B(-1,-2),C(-1,0).设D(x, )
① 如图1,过点 A 作BC的平行线,不存在点 D.
②如图2,当BD ∥AC时,∠ACE=∠DBF,所以
解方程得x=-1或x=6.此时.
③如图3,当CD∥AB时,∠ABE=∠DCF,所以
解方程 得x=1或x=-2.此时D(1,2)或(-2,-1).
9满分解答
①如图1,当 DE ∥QB 时,∠AQP =90°.
在Rt△AQP 中, 所以 解得
②如图2,当DE ∥BC 时,
在 Rt△AQP 中, 所以 解得
10.满分解答
易得抛物线的解析式为 直线OC 的解析式为
设
如图1,作ME⊥AB 于E,作 PF⊥AB 于F.
如果四边形ABPM 为等腰梯形,那么AE=BF.所以.
解方程 整理,得
解得 或x=2(P、C重合,舍去).
所以点 P 的坐标为 (如图2所示).
11满分解答
(1)由 当x=0时,y=1.
所以B(0,1),OB=1.
解方程 得x=-3.
所以A(-3,0),OA=3.
由A(-3,0)、C(2,0),得AC=5.
所以
(2) 第一种情况,过点A 作BC 的平行线交y轴于点D.
由 B(0,1)、C(2,0),得直线 BC 的解析式为
设直线 AD 的解析式为 代入点A(-3,0),得
解得 所以点 D 的坐标为(
第二种情况,过点C 作AB 的平行线交y轴于点D.
由直线 AB 的解析式为 设直线CD 的解析式为
代入点C(2,0),得 解得 所以点D 的坐标为
12满分解答
(1)由 得A(-3,0), B(0,-4).所以 因为 所以OC=2.所以C(2,0).
(2)由B(0, - 4)、C(2,0),得直线 BC 的解析式为y=2x-4.
因为四边形 AECD 为梯形,所以 AD ∥BC.所以kAD=kBC=2.
设直线AD 的解析式为y=2x+b,代入A(-3,0),得-6+b=0.解得b=6.
所以直线AD 的解析式为y=2x+6, D(0,6).
所以
因为点 E 为线段BC 的中点,所以
所以
13.满分解答
(1)设y= kx+4,代入B(2,0),得2k+4=0,解得k=-2.所以y=-2x+4.
(2)如图2,设C(a,0),已知A(0,4), B(2,0),AC=BC,所以
所以 解得a=-3.所以C(-3,0).
设CD 的解析式为y=-2x+b,代入C(-3,0),得6+b=0.解得b=-6.
所以y=-2x-6,D(0,-6).
因为四边形ABDE 是等腰梯形,可知AB∥ED.设E(m,-2m-6).
【方法一】由腰AE=BD,根据 列方程.
因为A(0,4)、B(2,0)、D(0,-6),所以
解得 (此时ABDE 是平行四边形,舍去).所以E(-6,6).
【方法二】由对角线AD=BE,根据 列方程.
因为A(0,4)、B(2,0)、D(0,-6),所以(
解得 (此时点 E 在点D 右侧,ABED 是平行四边形,舍去).
所以E(-6,6).
【方法三】由 HE=HD,根据 列方程.
因为A(0,4)、B(2,0)、D(0, - 6),所以 H(1,2).
所以
解得 (此时点 E 与点D 重合,舍去).
所以E(-6,6).
【方法四】由CA=CB,根据 列方程.
因为E(m,-2m-6)、D(0,-6),所以
所以
解得m=-6.所以E(-6,6).
14.满分解答
(1)将点A(4,0)代入y= kx+8,得4k+8=0.解得k=-2.
(2)如图2,因为点C是AB 的中点,所以点C的坐标为(2,4).
因为OC 是直角三角形AOB 斜边上的中线,所以CB=CO.
因此CB、CO 是菱形的邻边,BO为菱形的对角线.
所以D、C两点关于y轴对称,点 D 的坐标是(-2,4).
(3)由O、D(-2,4),可得直线OD 的解析式为y=-2x.
所以OD ∥AB.
因为A、O、B三点是确定的,过△AOB 的每个顶点画对边的平行线,与直线OD 交于点E.
①如图3,过点 A 画OB 的平行线,四边形 BOEA 是平行四边形.
②如图4,过点 B 画OA 的平行线,四边形EOAB 是平行四边形.
③如图5,因为OD ∥AB,如果BE=AO,那么四边形BEOA是等腰梯形.
设点E 的坐标为(x,-2x).由 得
整理,得
因式分解,得(x+4)(5x+12)=0.
所以x=-4,或
当x=-4时,点E的坐标为(-4,8),此时EB∥x轴,四边形BEOA 是平行四边形.
当 时,点E的坐标为
15满分解答
(1) 联立y=-x+7和 解得x=3,y=4.所以A(3,4).
解方程-x+7=0,得x=7.所以B(7,0).
(2)①(i)如图2,当点P在OC上时,OP=BR=t,CP=4-t,OR=7-t.
所以
整理 解得t=2,或t =6(点 P 不在OC 上,舍去).
(ii)如图3,当点P 在CA上时,PA≤3,PA对应的高为4,所以△APR的面积小于等于6.
② 在①的条件下,A(3,4)、P(0,2)、Q(5,2).所以PQ∥x轴.
分三种情况讨论等腰梯形:
(i) 如图4,对称轴是 PQ 的垂直平分线,AM ∥PQ.
此时点A(3,4)关于直线 对称的点 M 的坐标为(2,4).
(ii)如图5,对称轴是AQ 的垂直平分线,PM∥AQ.
因为AE=QE,所以设PF=MF=m,那么M(m,2-m).
由对角线AM=PQ=5,得. 所以(
整理,得 解得m=3,或m=-2.
当m=3时,M(3,-1).
当m=-2时,四边形MPQA 是平行四边形,图中点M'对应的位置.
(iii)如图6,对称轴是AP 的垂直平分线,QM∥AP.
因为AE:PE=2:3,所以设M(5-3m,2-2m).
由腰 得 所以
整理,得 解得 或m=1.
当 时,
当m=1时,四边形 PMQA 是平行四边形,图中点. 对应的位置.
16.满分解答
(1) 如图2,在Rt△OBP 中,OB=8,PB=6,所以OP =10.
因为AC是Rt△AOP 的斜边OP 上的中线,所以
(2) 如图2,因为C是OP 的中点,所以
在Rt△AOP 中,AP=x,OP =10,所以,
所以
又因为S△BOP =24,所以
定义域是0
作 PE⊥AC于E,那么△PEC≌△ODC.
所以CE=CD=3,PE=OD=4.
在Rt△AEP 中,AE=5-3=2, PE=4,所以.
②如图4,当AP∥CB时,作CD⊥OB于D,作AH⊥OB 于H,作PF⊥AH于F.
由 设AF=3m,PF=4m,那么AP=5m.
在Rt△AOH 中,AH=6+3m,OH=8-4m,所以(
在Rt△AOP 中,
所以
解得 或m=0(舍去).
此时
同课章节目录
