2025年中考数学复习-- 面积的存在性问题专项练习(含解析)
文档属性
| 名称 | 2025年中考数学复习-- 面积的存在性问题专项练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
面积的存在性问题
1.如图1,在平面直角坐标系中,抛物线 与x轴交于A、B两点(点A 在点B 的左侧),与y轴交于点C.
(1)求点A、B、C的坐标;
(2) 点P 从点A 出发,在线段AB 上以每秒2个单位长度的速度向点 B 运动,同时点Q 从点B 出发,在线段 BC 上以每秒1个单位长度的速度向点C 运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t 秒,求运动时间为多少秒时,△PBQ 的面积最大,并求出最大面积;
(3)在(2)的条件下,当△PBQ面积最大时,在BC 下方的抛物线上是否存在点M,使△BMC的面积是△PBQ 面积的1.6倍 若存在,求点M 的坐标;若不存在,请说明理由.
2 如图1,在平面直角坐标系中,函数 (m为常数,m>1,x>0)的图像经过点P(m,1)和Q(1,m),直线PQ与x轴、y轴分别交于C、D两点.点M(x,y)是该函数图像上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A、B.
(1) 求∠OCD 的度数;
(2)当m=3,1(3)当m=5时,矩形OAMB 与△OPQ 的重叠部分的面积能否等于4.1 请说明你的理由.
3.如图1,抛物线 与x轴交于点A 和点B(5,0),与y轴交于点C,抛物线的顶点为 P.
(1) 求抛物线的表达式并写出顶点 P 的坐标;
(2)在x轴上方的抛物线上有一点D,若∠ABD=∠ABP,试求出点 D 的坐标;
(3) 设在直线 BC 下方的抛物线上有一点Q,若S△BCQ=15,试求出点 Q 的坐标.
专题直击
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,设在直线BC下方的抛物线上有一点 Q,若S△BCQ=15,试求出点 Q 的坐标.
4.如图,矩形ABCD 的顶点C在y轴右侧沿抛物线. 滑动,在滑动过程中CD∥x轴,CD=1,AB在CD的下方.当点D在y轴上时,AB落在x轴上.当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.
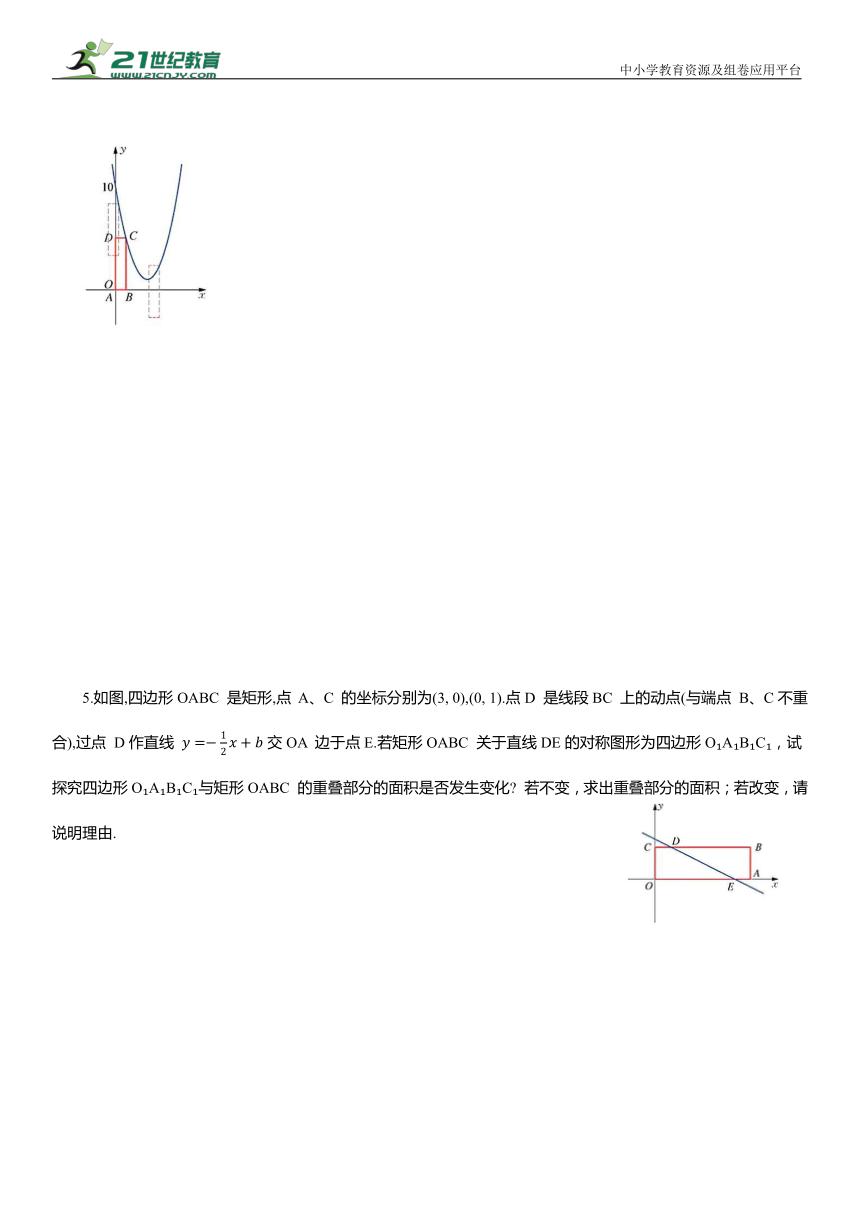
5.如图,四边形OABC 是矩形,点 A、C 的坐标分别为(3, 0),(0, 1).点D 是线段BC 上的动点(与端点 B、C不重合),过点 D作直线 交OA 边于点E.若矩形OABC 关于直线DE的对称图形为四边形O A B C ,试探究四边形O A B C 与矩形OABC 的重叠部分的面积是否发生变化 若不变,求出重叠部分的面积;若改变,请说明理由.
6.如图,已知扇形AOB 的半径为2,圆心角∠AOB=90°,点C是弧AB 上的一个动点,( OA 于D, CE⊥OB 于E,求四边形ODCE 的面积的最大值.
7.如图,二次函数 的图象与x 轴交于A、B两点,顶点M 的坐标为(1,-4).
(1)求A、B两点的坐标;
(2) 设直线AM 与y轴交于点C,求△BCM 的面积;
(3) 在抛物线上是否还存在点 P,使得S△PMB =S△BCM,如存在,求出点 P 的坐标;如果不存在,请说明理由.
8.如图,在平面直角坐标系中,一次函数y=x+3的图像与y轴相交于点A,二次函数. 的图像经过点A、B(1,0), D为顶点.
(1) 求这个二次函数的解析式,并写出顶点 D 的坐标;
(2) 将上述二次函数的图像沿 y轴向上或向下平移,使点 D 的对应点C在一次函数y=x+3的图像上,求平移后所得图像的表达式;
(3) 设点P 在一次函数y=x+3的图像上,且.S△ABP=2S△ABC,求点P 的坐标.
9.(1)如图1,已知平行四边形ABCD,如果直线l同时平分平行四边形ABCD 的周长和面积,那么直线l一定经过哪个确定的点
(2)如图2,已知等腰梯形ABCD,如果直线l同时平分等腰梯形ABCD 的周长和面积,那么直线l也经过一个确定的点吗
(3)如图3,已知梯形ABCD,是否存在直线l同时平分梯形ABCD 的周长和面积 如果存在,那么直线l也经过一个确定的点吗
(4)如图4,在△ABC中,∠C=90°,AC=6,BC=8,设直线l与斜边AB交于点E,与直角边交于点F,设AE=x,是否存在直线l同时平分△ABC的周长和面积 若存在直线l,求出x的值;若不存在直线l,请说明理由.
10.如图1,已知边长为2的正方形ABCD中,AC为对角线,点E 在线段AC上(点E 与点A、C不重合),过点 E 作EF⊥BC,垂足为点 F,联结ED 和DF.
(1) 说明△EFD 与△EFC 的面积相等;
(2)设.AE=x,S△EDF=y(S△EDF表示△EDF 的面积),求y关于x的函数解析式,并写出自变量x 的取值范围;
(3) 当△EDC 为等腰三角形时,求线段AE 的长.
11.如图1,在正方形ABCD中,AB=4,点M是边BC的中点,点 E 是边AB上的一个动点,作EG⊥AM 交AM 于点G, EG 的延长线交线段CD 于点 F.
(1)如图1,当点E 与点B 重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD 的面积是y,求y与x 的函数解析式,并写出定义域.
12.如图1,在矩形ABCD中,AB=1,对角线AC、BD相交于点O,过点O作EF⊥AC 分别交射线AD 与射线CB 于点E 和点F,联结CE、AF.
(1) 如图,求证:四边形AFCE 是菱形;
(2)当点E、F 分别在边AD和BC上时,如果设AD=x,菱形AFCE的面积是 y,求y关于x的函数关系式,并写出x的取值范围;
(3) 如果△ODE 是等腰三角形,求AD 的长度.
13.如图1,在梯形ABCD中,AD ∥BC,AB=CD,BC=10,对角线AC、BD 相交于点O,且AC⊥BD.设AD=x,△AOB 的面积为y.
(1) 求∠DBC 的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图2,设点 P、点Q分别是边BC、AB 的中点,分别联结OP、OQ、PQ.如果△OPQ是等腰三角形,求AD的长.
14.如图1,已知正方形 ABCD 的边长为3,菱形 EFGH 的三个顶点E、G、H 分别在正方形的边AB、CD、DA 上,AH =1,联结CF.
(1)当DG=1时,求证:菱形EFGH 为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x 的取值范围;
(3)当 时,求∠GHE 的度数.
15.如图1,已知在等腰梯形ABCD中,AD∥BC,AD=AB=CD=6厘米, 点P在边AD上以每秒2厘米的速度从点 D 出发,向点A 运动;点Q在边AB 上以每秒1厘米的速度从点 B 出发,向点 A 运动.已知 P、Q两点同时出发,当其中一个点到达终点时,另一个点也随之停止运动.设两个点运动的时间为 t 秒,联结PC、QD.
(1)如图1,若四边形 BQDC 的面积为S平方厘米,求S关于t的函数解析式并写出函数定义域;
(2)若PC与QD 相交于点E,且∠PEQ=60°,求t 的值.
16.如图1,在梯形ABCD中,AD ∥BC,AC=BC=4,∠D=90°,M、N分别是AB、DC的中点,过点B作BE⊥AC交射线AD于点E,BE 与AC 交于点F.
(1) 当∠ACB=30°时,求 MN 的长;
(2)设线段CD=x,四边形ABCD的面积为y,求y与x的函数关系式及其定义域;
(3) 联结CE,当CE=AB 时,求四边形ABCE 的面积.
17.如图1,在梯形 ABCD 中, AD ∥BC, ∠B =90°, ∠C =45°,AB=8,BC=14,点E、F分别在边AB、CD上,EF∥AD,点P与AD在直线EF的两侧,∠EPF=90°, PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
(1) 求边AD 的长;
(2)如图,当点 P 在梯形ABCD 内部时,求y关于x的函数解析式,并写出定义域;
(3) 如果MN 的长为2,求梯形AEFD 的面积.
18如图1,梯形ABCD中,∠BCD=90°, AD=2, BC=4,CD=4 ,对角线AC、BD相交于点O.点E为BD上一动点(不与点B、D重合).联结AE、CE.设DE=x,△AED的面积为y.
(1) 求y关于x的函数关系式,并写出定义域;
(2) 当AE=CE时,求x 的值;
(3)当x取何值时,△AOD 与△EOC 面积相等 写出你的猜想,并证明你的结论.
19如图1,在平面直角坐标系中,点A 的坐标为(0,4),点B 是x轴上一点,以AB 为边,在AB 的一侧作正方形ABCD,对角线AC、BD相交于点E,过点C向x轴作垂线,垂足为F,点G是OF 的中点,联结EG.
(1) 如果点 B 的坐标为(1, 0),求点 C 的坐标;
(2) 当点 B 在x轴正半轴上时,如果点 B 的坐标为(a, 0),△BEG 的面积为S,写出S关于a 的函数解析式及定义域;
(3) 当△BEG 的面积为 时,求线段 EG 的长.
1.满分解答
(1)由 得A(-2,0),B(3,0),C(0,-4).
(2)如图2,在Rt△BOC中,OB=3,OC=4,所以
作QH ⊥x 轴于H.在 Rt△BQH 中,
所以
当 时,△PBQ的面积最大,最大值为
(3) 如图3,过点M作y轴的平行线交BC 于N.
由 B(3,0)、C(0,-4),得直线BC 的解析式为
设 那么
所以
解方程 整理,得
解得x=1,或x=2.所以点M的坐标为(1,-4)或(
考点伸展
第(3)题中, 面积的最大值是多少呢
由 可知当 时,△MBC 的取得最大值,最大值为 这是一个典型结论,当点 N 是BC 的中点时, 的面积最大.
2.满分解答
(1) 如图2,作 PP'⊥x 轴于P',作QQ'⊥y轴于Q'.设PP'与QQ'交于点K.由 得∠KQP=45°.所以∠OCD=45°.
(2) 如图3,当m=3时, P(3,1), Q(1, 3).所以
由直线 PQ 的解析式y=-x+4,得C(4,0).所以OC=4.
如果△OPM∽△OCP,那么 所以
由 得
整理,得 解得 或
所以x=2,或 所以 或( ,2).
检验:当 时,
所以
所以 所以 要舍去.所以符合条件的点M的坐标是(
(3)如图4,设MA 与OP 交于点G, MB 与OQ 交于点 H.
由 得 所以
由 得 所以
所以重叠部分的面积
解方程 整理,得
因为Δ=81--100<0,所以此方程无实数根.所以重叠部分的面积不能为4.1.如图5,当x>5时,重叠部分的面积小于△OPP'的面积,所以不可能为4.1.当0考点伸展
第(3)题情景下,重叠部分的面积的最大值是多少呢
由 可知重叠部分面积的最大值为4.
3.满分解答
(1) 将点 B(5, 0)代入 得.解得b=-6.
所以 顶点 P 的坐标为(3,-4).
(2)如图2,作DN⊥x轴于N.设抛物线的对称轴与x轴交于点M.
由 tan∠ABD=tan∠ABP,得
设点 D 的坐标为 那么
解得x=-1.所以点D 的坐标为(--1, 12).
(3)由B(5,0)、C(0,5),可知 直线 BC 与x 轴负半轴的夹角为45°.
设 BC边上的高为h,那么 解得
如图3,设y轴上点C下方的点G到直线BC 的距离( 那么 过点G 作BC 的平行线与抛物线的交点就是要求的点Q,这条直线为 解方程组 得 或 所以 或(3,--4).
4.满分解答
当x=1时, 所以 BC边的长为5.
如图1,当矩形ABCD 在x轴上方部分的面积与这个矩形面积的比为1:5时,点C的纵坐标为1.
解方程 得
此时点C 的坐标为(3,1).
如图2,当矩形ABCD 在x轴上方部分的面积与这个矩形面积的比为4:5时,点C的纵坐标为4.
解方程 得
此时点C的坐标为 或
5.满分解答
如图1,因为四边形O A B C 与矩形OABC关于直线DE 对称,因此DM=DN,那么重叠部分是邻边相等的平行四边形,即四边形 DMEN 是菱形.
作DH⊥OA,垂足为 H.
由于CD=2b-2,OE=2b,所以EH=2.
设菱形 DMEN 的边长为m.
在Rt△DNH 中,DH=1, NH=2-m,DN=m,所以 解得
所以重叠部分菱形 DMEN 的面积为-
6.满分解答
如图1,图2,设矩形ODCE 的对角线交于点F,那么OF =1为定值.
作OH⊥DE于H,那么OH≤OF.
因为DE=2为定值,因此当OH与OF 相等时(如图3),△DOE的面积最大,最大值为1.所以矩形ODCE 的面积的最大值为2.
7.满分解答
(1) 由 ,得A(-1,0), B(3,0).
(2)因为A、M到y轴的距离相等,所以C是AM 的中点.所以C(0,-2).
因此
(3)过点C作BM 的平行线与抛物线有两个交点,这两个交点都是符合条件的点 P.设P(x 由 PC ∥BM,得∠CPE=∠BMF.所以 解方程 得 所以 或
8.满分解答
(1)由y=x+3,得A(0,3).
将A(0, 3)、B(1, 0)分别代入 得 解得
所以二次函数的解析式为 顶点为 D(-1,4).
(2)如图1,当x=--1时,y=x+3=2.
所以点 C 的坐标为(-1, 2).
所以平移后的抛物线的解析式为.
(3)如图2, △ABP 与△ABC 是共底三角形,AB 是公共的底边.
当 时,点P 到直线AB 的距离等于点C 到直线AB 的距离的2倍.
所以PA=2PC.因此 xp=±2xc=±2(如图3).
所以点 P 的坐标为(2, 5)或(-2, 1).
9.满分解答
(1) 如图1,直线l一定经过平行四边形的对角线的交点.
(2) 如图2,直线l一定经过梯形中位线的中点.
(3)如图3,如果直线l经过梯形中位线的中点,并且与两底相交,那么直线l平分梯形的面积,但不一定平分梯形的周长.当等腰梯形时,直线l同时平分周长和面积.
(4)△ABC 的周长为24,面积为24.
如图4,点F在AC上,假设直线 EF 同时平分△ABC的周长和面积,那么AE=x,AF=
解方程 得
当 ,此时点 F 不在AC上.所以取
如图5,点F 在BC上,假设直线 EF 同时平分△ABC 的周长和面积,那么AE=x, BE =10-x,BF=12-(10-x)=2+x,EH= (10-x).
方程 整理,得 此方程无实数根.
10.满分解答
(1) 如图2,因为四边形ABCD 为正方形,所以∠BCD=90°.
因EF⊥BC,所以∠EFC=90°.所以EF ∥DC.
由平行线间的距离处处相等,得△EFD 与△EFC 为同底等高三角形.
所以△EFD 与△EFC 的面积相等.
(2)如图2,因为四边形 ABCD 为正方形,所以∠ACB=∠ACD =45°.
在Rt△ABC中,AB=BC=2,所以.
所以.
在Rt△EFC中, 设.EF=FC=m.
由勾股定理,得 整理,得
所以
所以
自变量的取值范围是(
(3) 分三种情况讨论△EDC 为等腰三角形.
①如图3,当CD=CE时,CE=2.所以.
②如图4,当EC=ED时,∠EDC=∠ECD=45°.所以∠ADE=45°.
所以 DE 为等腰直角三角形ADC 的角平分线.
由等腰三角形三线合一,
③如图5,当DC=DE时,∠DEC=∠ECD=45°.
此时点 E 与点A 重合,不符合题意,舍去.
11.满分解答
(1)如图2,由正方形ABCD,得AB=BC,∠ABC=∠C=90°.
所以
因为EG⊥AM,所以∠EGA=90°.
所以∠1+∠3=90°.
所以∠1=∠2.
在△ABM与△BCF中,∠1=∠2,AB=BC,∠ABC=∠C,所以△ABM≌△BCF.所以BM=CF.
(2)如图3,过点E作EH⊥DC 于H,得矩形 BCHE.
所以EH=BC=AB,CH=BE,∠EHF=90°.
由(1),得∠1=∠2.
在△ABM与△EHF 中,∠1=∠2,AB=EH,∠B=∠EHF,所以△ABM≌△EHF.
所以HF=BM=2.
因为BE=x,所以AE=4-x,DF=DC-CH-HF=2-x.
所以 ,定义域是0≤x<2.
12满分解答
(1) 因为四边形ABCD 是矩形,所以OA=OC, DA∥CB.
所以∠1=∠2.
在△AOE 和△COF 中,∠1=∠2,OA=OC,∠AOE=∠COF,所以△AOE≌△COF.所以OE=OF.
又因为EF⊥AC,所以四边形AFCE 是菱形.
(2)设菱形的边长为m.
在Rt△DEC中,EC=m,DE=x-m,DC=1,由勾股定理,得(
整理,得 解得
所以 定义域是x>0.
(3) 因为四边形ABCD 是矩形,所以OC=OD,∠5=∠6.
当△ODE 是等腰三角形时,分两种情况讨论.
①如图4,当点E 在线段AD 上时,△ODE 为钝角三角形,所以只可能存在EO=ED.此时,∠3=∠4.
因为∠ADC=90°,所以∠3+∠5=90°.
因为∠EOC=90°,所以∠4+∠7=90°.
根据等角的余角相等,得∠5=∠7.所以∠5=∠6=∠7=60°,∠3=30°.
在Rt△ADB 中,∠3=60°, AB=1,所以BD=2.所以.
②如图5,当点 E 在线段AD 的延长线上时,△ODE 为钝角三角形,所以只可能存在DO=DE.此时,∠8=∠4.
因为∠EDC=90°,所以∠8+∠EMD=90°.
因为∠EOC=90°,所以∠6+∠OMC=90°.
根据等角的余角相等,得. 所以 因为 所以 所以 在 中, 设 由勾股定理,得 解得 (不符合题意,舍去), 所以
13满分解答
(1) 如图3,过点D作DK ∥AC交BC 延长线于点K,得平行四边形ADKC.
所以AC=DK,AD=CK=x.
由等腰梯形的对角线相等,得AC=BD.所以BD=DK.
又AC⊥BD,所以∠BOC=90°.
所以∠BDK=90°,∠DBC=45°.
(2) 如图3,过点D 作DN⊥BC 于N,过点O作OH⊥BC 于H.
由(1),在等腰直角三角形DBK 中,
在等腰直角三角形OBC 中,
所以
所以 自变量的取值范围是x>0且x≠10.
(3) 如图4,过点A 作AM⊥BC 于M.
由(2),在 Rt△BND中, 所以
在 Rt△ABM中, 所以
在△ABC 中,PQ 是△ABC 的中位线,
在 Rt△AOB 中,OQ 是斜边上的中线,
在等腰直角三角形 BOC 中,
如图5,△OPQ 是等腰三角形,分三种情况讨论.
①当PQ=PO时, 解得 此时.
②当OQ=OP 时, 解得 (均不符合题意,舍去).
③当QO=QP 时, 解得x=0(不符号题意,舍去).
综上所述,如果△OPQ 是等腰三角形,
14.满分解答
(1) 如图2,因为四边形ABCD 是正方形,所以∠D=∠A =90°.
因为四边形 EFGH 是菱形,所以 HG=EH.
在 和 中,HG=EH,DG=AH=1,所以 所以∠1=∠2.
因为 所以 所以∠GHE=90°.
所以菱形 EFGH 为正方形.
(2) 如图3,过点 F 作DA 的平行线,交 DC 延长线于M.
所以
因为正方形ABCD 和菱形EFGH,所以HE=FG,DC∥AB,GF ∥HE.
所以 所以△HAE≌△FMG,MF=AH=1.
所以 定义域为0≤x≤
(3)过点G作GK⊥AB于K.
在Rt△DGH 中, 所以
在 中, 所以
在 中, 所以
所以 是等边三角形.所以.
15.满分解答
(1)如图2,过点A作AG⊥BC于G,过点D作DH⊥BC于H,得到矩形AGHD.
因为四边形ABCD为等腰梯形,所以∠C=∠B=60°,∠BAD=∠ADC=120°.
在Rt△ABG中,∠B=60°, AB=6cm,所以∠BAG=30°, BG=3cm,AG=3 cm.
同理可得,CH=3cm,BC=3+6+3=12cm.
所以
如图3,过点 D 作DM⊥AB 交BA 延长线于点M.
在Rt△ADM 中, 所以 因为BQ= tcm,所以AQ=(6-t) cm.
所以
所以
定义域是0(2)如图4,在△EDC 中,因为∠DEC=∠PEQ=60°,所以∠1+∠3=120°.
又因为∠ADC=∠2+∠3=120°,所以∠1=∠2.
在 和 中, 所以 所以 所以解得
16.满分解答
(1) 如图2,因为AD∥BC,所以∠CAD=∠ACB=30°.
在Rt△ACD 中,∠CAD=30°, AC=4,所以CD=2.
由勾股定理,得
如图3,因为MN 是梯形ABCD 的中位线,所以.
(2)如图4,在Rt△ACD中,AC=4,CD=x,由勾股定理,得. 所以 定义域是0(3)如图5,当CE=AB时,四边形ABCE 是等腰梯形.
此时对角线BE=AC=4.
【方法一】如图5,过点 E 作AC 的平行线交BC 的延长线于点 H.所以四边形ACHE 是平行四边形.
所以AE=CH.根据等底等高的三角形面积相等,得S△ABE =S△ECH.
所以
因为BE⊥AC,所以BE⊥EH.
所以 是等腰直角三角形, 所以
【方法二】如图6,因为
所以
17.满分解答
(1) 如图2,作 DD'⊥BC于D'.
在Rt△DD'C中, 所以
所以.
(2)如图3,过点 F 作AB 的平行线交AD 的延长线于点A',交BC 于点B'.
在等腰直角三角形DA'F中,
在等腰直角三角形FB'C中,
过点 P 作PQ⊥EF 于Q, PQ交AD 于G,交BC 于H.
在等腰直角三角形 PEF 中,
在等腰直角三角形 PMN 中,
由GH=GQ+PQ+PH=8,得
整理,得y=-3x+10.定义域是
定义域是这样确定的:
当MN=y=0时,由-3x+10=0,得 (如图4所示).
当MN=y=AD=6时,由-3x+10=6,得 (如图5所示).
(3)MN=2存在两种情况:
① 如图6,当点 P 在梯形内部时, MN=2.
解方程-3x+10=2,得.
此时在梯形AEFD中,
所以梯形AEFD 的面积为
②如图7,当点 P 在梯形外部时, MN=2.
由GH=GQ+PQ-PH =8,得
整理,得y=3x-10.
解方程3x-10=2,得x=4.
此时在梯形AEFD中,AE=4,AD=6,EF=6+4=10.所以梯形AEFD的面积为32.
18满分解答
(1)如图2,在Rt△BCD中,BC=4,CD=4 ,所以BD=8,∠BDC=30°.
由△AED 和△ABD 是等高三角形,可得
因为 所以
定义域是0(2)如图3,在Rt△DEM中,∠BDC=30°, DE=x,所以
如图4,作EN⊥AD于N,作EM⊥DC 于M.
在Rt△AEN 中, 所以
在Rt△EMC 中, 所以
因为AE=CE,所以.
所以 解得
(3)【方法一】① 如图5,当点 E 在OB 上时,由S△EOC =S△AOD,得S△EDC =S△ADC.
由△EDC 和△ADC 是同底三角形,所以高EM=AD=2.所以ED=4.
②如图6,当点 E 在OD 上时,此时 所以( 如图7,因为AD ∥BC,所以 又因为BD=8,所以 所以 所以
【方法二】① 当点 E 在OB 上时,如图8,设G、H 分别为OB、OC 的中点,那么GH 为△OBC 的中位线.
所以
所以∠ADO=∠HGO,∠DAO=∠GHO,AD=HG.
所以△AOD≌△HOG,所以S△AOD =S△HOG.
因为点 H 是OC 中点,所以S△co;=2S△HOG =2S△AOD.
所以当点 E为OG 中点时,
因为 所以
因为 所以
②如图6,当点 E 在OD 上时,
19满分解答
(1)如图2,因为∠1+∠3=90°,∠2+∠3=90°,所以∠1=∠2.又因为∠BFC=∠AOB=90°, BC=AB,所以△BFC≌△AOB.所以BF=AO=4,FC=OB=1.所以点C的坐标为(5,1).
(2)如图3,当A(0,4)、B(a,0)时,BF=AO=4,FC=OB=a,所以C(4+a,a).
因为CF ∥AO,所以四边形AOFC 是梯形.
因为E、G分别是AC、OF 的中点,所以EG 是梯形AOFC 的中位线.
所以
分两种情况求 S 关于a 的函数解析式,
①如图4,当B在G左侧时,(
此时
②如图5,当B在G右侧时, 此时
(3)①如图4,当B在G左侧,0②如图5,当B在G右侧,a>4时,解方程 得
此时正方形 EHOG 的边长
③如图6,
由 得a=±2(舍去正值).此时EG=1.
④如图7,
由 得 (舍去正值).此时
面积的存在性问题
1.如图1,在平面直角坐标系中,抛物线 与x轴交于A、B两点(点A 在点B 的左侧),与y轴交于点C.
(1)求点A、B、C的坐标;
(2) 点P 从点A 出发,在线段AB 上以每秒2个单位长度的速度向点 B 运动,同时点Q 从点B 出发,在线段 BC 上以每秒1个单位长度的速度向点C 运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t 秒,求运动时间为多少秒时,△PBQ 的面积最大,并求出最大面积;
(3)在(2)的条件下,当△PBQ面积最大时,在BC 下方的抛物线上是否存在点M,使△BMC的面积是△PBQ 面积的1.6倍 若存在,求点M 的坐标;若不存在,请说明理由.
2 如图1,在平面直角坐标系中,函数 (m为常数,m>1,x>0)的图像经过点P(m,1)和Q(1,m),直线PQ与x轴、y轴分别交于C、D两点.点M(x,y)是该函数图像上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A、B.
(1) 求∠OCD 的度数;
(2)当m=3,1
3.如图1,抛物线 与x轴交于点A 和点B(5,0),与y轴交于点C,抛物线的顶点为 P.
(1) 求抛物线的表达式并写出顶点 P 的坐标;
(2)在x轴上方的抛物线上有一点D,若∠ABD=∠ABP,试求出点 D 的坐标;
(3) 设在直线 BC 下方的抛物线上有一点Q,若S△BCQ=15,试求出点 Q 的坐标.
专题直击
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,设在直线BC下方的抛物线上有一点 Q,若S△BCQ=15,试求出点 Q 的坐标.
4.如图,矩形ABCD 的顶点C在y轴右侧沿抛物线. 滑动,在滑动过程中CD∥x轴,CD=1,AB在CD的下方.当点D在y轴上时,AB落在x轴上.当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.
5.如图,四边形OABC 是矩形,点 A、C 的坐标分别为(3, 0),(0, 1).点D 是线段BC 上的动点(与端点 B、C不重合),过点 D作直线 交OA 边于点E.若矩形OABC 关于直线DE的对称图形为四边形O A B C ,试探究四边形O A B C 与矩形OABC 的重叠部分的面积是否发生变化 若不变,求出重叠部分的面积;若改变,请说明理由.
6.如图,已知扇形AOB 的半径为2,圆心角∠AOB=90°,点C是弧AB 上的一个动点,( OA 于D, CE⊥OB 于E,求四边形ODCE 的面积的最大值.
7.如图,二次函数 的图象与x 轴交于A、B两点,顶点M 的坐标为(1,-4).
(1)求A、B两点的坐标;
(2) 设直线AM 与y轴交于点C,求△BCM 的面积;
(3) 在抛物线上是否还存在点 P,使得S△PMB =S△BCM,如存在,求出点 P 的坐标;如果不存在,请说明理由.
8.如图,在平面直角坐标系中,一次函数y=x+3的图像与y轴相交于点A,二次函数. 的图像经过点A、B(1,0), D为顶点.
(1) 求这个二次函数的解析式,并写出顶点 D 的坐标;
(2) 将上述二次函数的图像沿 y轴向上或向下平移,使点 D 的对应点C在一次函数y=x+3的图像上,求平移后所得图像的表达式;
(3) 设点P 在一次函数y=x+3的图像上,且.S△ABP=2S△ABC,求点P 的坐标.
9.(1)如图1,已知平行四边形ABCD,如果直线l同时平分平行四边形ABCD 的周长和面积,那么直线l一定经过哪个确定的点
(2)如图2,已知等腰梯形ABCD,如果直线l同时平分等腰梯形ABCD 的周长和面积,那么直线l也经过一个确定的点吗
(3)如图3,已知梯形ABCD,是否存在直线l同时平分梯形ABCD 的周长和面积 如果存在,那么直线l也经过一个确定的点吗
(4)如图4,在△ABC中,∠C=90°,AC=6,BC=8,设直线l与斜边AB交于点E,与直角边交于点F,设AE=x,是否存在直线l同时平分△ABC的周长和面积 若存在直线l,求出x的值;若不存在直线l,请说明理由.
10.如图1,已知边长为2的正方形ABCD中,AC为对角线,点E 在线段AC上(点E 与点A、C不重合),过点 E 作EF⊥BC,垂足为点 F,联结ED 和DF.
(1) 说明△EFD 与△EFC 的面积相等;
(2)设.AE=x,S△EDF=y(S△EDF表示△EDF 的面积),求y关于x的函数解析式,并写出自变量x 的取值范围;
(3) 当△EDC 为等腰三角形时,求线段AE 的长.
11.如图1,在正方形ABCD中,AB=4,点M是边BC的中点,点 E 是边AB上的一个动点,作EG⊥AM 交AM 于点G, EG 的延长线交线段CD 于点 F.
(1)如图1,当点E 与点B 重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD 的面积是y,求y与x 的函数解析式,并写出定义域.
12.如图1,在矩形ABCD中,AB=1,对角线AC、BD相交于点O,过点O作EF⊥AC 分别交射线AD 与射线CB 于点E 和点F,联结CE、AF.
(1) 如图,求证:四边形AFCE 是菱形;
(2)当点E、F 分别在边AD和BC上时,如果设AD=x,菱形AFCE的面积是 y,求y关于x的函数关系式,并写出x的取值范围;
(3) 如果△ODE 是等腰三角形,求AD 的长度.
13.如图1,在梯形ABCD中,AD ∥BC,AB=CD,BC=10,对角线AC、BD 相交于点O,且AC⊥BD.设AD=x,△AOB 的面积为y.
(1) 求∠DBC 的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图2,设点 P、点Q分别是边BC、AB 的中点,分别联结OP、OQ、PQ.如果△OPQ是等腰三角形,求AD的长.
14.如图1,已知正方形 ABCD 的边长为3,菱形 EFGH 的三个顶点E、G、H 分别在正方形的边AB、CD、DA 上,AH =1,联结CF.
(1)当DG=1时,求证:菱形EFGH 为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x 的取值范围;
(3)当 时,求∠GHE 的度数.
15.如图1,已知在等腰梯形ABCD中,AD∥BC,AD=AB=CD=6厘米, 点P在边AD上以每秒2厘米的速度从点 D 出发,向点A 运动;点Q在边AB 上以每秒1厘米的速度从点 B 出发,向点 A 运动.已知 P、Q两点同时出发,当其中一个点到达终点时,另一个点也随之停止运动.设两个点运动的时间为 t 秒,联结PC、QD.
(1)如图1,若四边形 BQDC 的面积为S平方厘米,求S关于t的函数解析式并写出函数定义域;
(2)若PC与QD 相交于点E,且∠PEQ=60°,求t 的值.
16.如图1,在梯形ABCD中,AD ∥BC,AC=BC=4,∠D=90°,M、N分别是AB、DC的中点,过点B作BE⊥AC交射线AD于点E,BE 与AC 交于点F.
(1) 当∠ACB=30°时,求 MN 的长;
(2)设线段CD=x,四边形ABCD的面积为y,求y与x的函数关系式及其定义域;
(3) 联结CE,当CE=AB 时,求四边形ABCE 的面积.
17.如图1,在梯形 ABCD 中, AD ∥BC, ∠B =90°, ∠C =45°,AB=8,BC=14,点E、F分别在边AB、CD上,EF∥AD,点P与AD在直线EF的两侧,∠EPF=90°, PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
(1) 求边AD 的长;
(2)如图,当点 P 在梯形ABCD 内部时,求y关于x的函数解析式,并写出定义域;
(3) 如果MN 的长为2,求梯形AEFD 的面积.
18如图1,梯形ABCD中,∠BCD=90°, AD=2, BC=4,CD=4 ,对角线AC、BD相交于点O.点E为BD上一动点(不与点B、D重合).联结AE、CE.设DE=x,△AED的面积为y.
(1) 求y关于x的函数关系式,并写出定义域;
(2) 当AE=CE时,求x 的值;
(3)当x取何值时,△AOD 与△EOC 面积相等 写出你的猜想,并证明你的结论.
19如图1,在平面直角坐标系中,点A 的坐标为(0,4),点B 是x轴上一点,以AB 为边,在AB 的一侧作正方形ABCD,对角线AC、BD相交于点E,过点C向x轴作垂线,垂足为F,点G是OF 的中点,联结EG.
(1) 如果点 B 的坐标为(1, 0),求点 C 的坐标;
(2) 当点 B 在x轴正半轴上时,如果点 B 的坐标为(a, 0),△BEG 的面积为S,写出S关于a 的函数解析式及定义域;
(3) 当△BEG 的面积为 时,求线段 EG 的长.
1.满分解答
(1)由 得A(-2,0),B(3,0),C(0,-4).
(2)如图2,在Rt△BOC中,OB=3,OC=4,所以
作QH ⊥x 轴于H.在 Rt△BQH 中,
所以
当 时,△PBQ的面积最大,最大值为
(3) 如图3,过点M作y轴的平行线交BC 于N.
由 B(3,0)、C(0,-4),得直线BC 的解析式为
设 那么
所以
解方程 整理,得
解得x=1,或x=2.所以点M的坐标为(1,-4)或(
考点伸展
第(3)题中, 面积的最大值是多少呢
由 可知当 时,△MBC 的取得最大值,最大值为 这是一个典型结论,当点 N 是BC 的中点时, 的面积最大.
2.满分解答
(1) 如图2,作 PP'⊥x 轴于P',作QQ'⊥y轴于Q'.设PP'与QQ'交于点K.由 得∠KQP=45°.所以∠OCD=45°.
(2) 如图3,当m=3时, P(3,1), Q(1, 3).所以
由直线 PQ 的解析式y=-x+4,得C(4,0).所以OC=4.
如果△OPM∽△OCP,那么 所以
由 得
整理,得 解得 或
所以x=2,或 所以 或( ,2).
检验:当 时,
所以
所以 所以 要舍去.所以符合条件的点M的坐标是(
(3)如图4,设MA 与OP 交于点G, MB 与OQ 交于点 H.
由 得 所以
由 得 所以
所以重叠部分的面积
解方程 整理,得
因为Δ=81--100<0,所以此方程无实数根.所以重叠部分的面积不能为4.1.如图5,当x>5时,重叠部分的面积小于△OPP'的面积,所以不可能为4.1.当0
第(3)题情景下,重叠部分的面积的最大值是多少呢
由 可知重叠部分面积的最大值为4.
3.满分解答
(1) 将点 B(5, 0)代入 得.解得b=-6.
所以 顶点 P 的坐标为(3,-4).
(2)如图2,作DN⊥x轴于N.设抛物线的对称轴与x轴交于点M.
由 tan∠ABD=tan∠ABP,得
设点 D 的坐标为 那么
解得x=-1.所以点D 的坐标为(--1, 12).
(3)由B(5,0)、C(0,5),可知 直线 BC 与x 轴负半轴的夹角为45°.
设 BC边上的高为h,那么 解得
如图3,设y轴上点C下方的点G到直线BC 的距离( 那么 过点G 作BC 的平行线与抛物线的交点就是要求的点Q,这条直线为 解方程组 得 或 所以 或(3,--4).
4.满分解答
当x=1时, 所以 BC边的长为5.
如图1,当矩形ABCD 在x轴上方部分的面积与这个矩形面积的比为1:5时,点C的纵坐标为1.
解方程 得
此时点C 的坐标为(3,1).
如图2,当矩形ABCD 在x轴上方部分的面积与这个矩形面积的比为4:5时,点C的纵坐标为4.
解方程 得
此时点C的坐标为 或
5.满分解答
如图1,因为四边形O A B C 与矩形OABC关于直线DE 对称,因此DM=DN,那么重叠部分是邻边相等的平行四边形,即四边形 DMEN 是菱形.
作DH⊥OA,垂足为 H.
由于CD=2b-2,OE=2b,所以EH=2.
设菱形 DMEN 的边长为m.
在Rt△DNH 中,DH=1, NH=2-m,DN=m,所以 解得
所以重叠部分菱形 DMEN 的面积为-
6.满分解答
如图1,图2,设矩形ODCE 的对角线交于点F,那么OF =1为定值.
作OH⊥DE于H,那么OH≤OF.
因为DE=2为定值,因此当OH与OF 相等时(如图3),△DOE的面积最大,最大值为1.所以矩形ODCE 的面积的最大值为2.
7.满分解答
(1) 由 ,得A(-1,0), B(3,0).
(2)因为A、M到y轴的距离相等,所以C是AM 的中点.所以C(0,-2).
因此
(3)过点C作BM 的平行线与抛物线有两个交点,这两个交点都是符合条件的点 P.设P(x 由 PC ∥BM,得∠CPE=∠BMF.所以 解方程 得 所以 或
8.满分解答
(1)由y=x+3,得A(0,3).
将A(0, 3)、B(1, 0)分别代入 得 解得
所以二次函数的解析式为 顶点为 D(-1,4).
(2)如图1,当x=--1时,y=x+3=2.
所以点 C 的坐标为(-1, 2).
所以平移后的抛物线的解析式为.
(3)如图2, △ABP 与△ABC 是共底三角形,AB 是公共的底边.
当 时,点P 到直线AB 的距离等于点C 到直线AB 的距离的2倍.
所以PA=2PC.因此 xp=±2xc=±2(如图3).
所以点 P 的坐标为(2, 5)或(-2, 1).
9.满分解答
(1) 如图1,直线l一定经过平行四边形的对角线的交点.
(2) 如图2,直线l一定经过梯形中位线的中点.
(3)如图3,如果直线l经过梯形中位线的中点,并且与两底相交,那么直线l平分梯形的面积,但不一定平分梯形的周长.当等腰梯形时,直线l同时平分周长和面积.
(4)△ABC 的周长为24,面积为24.
如图4,点F在AC上,假设直线 EF 同时平分△ABC的周长和面积,那么AE=x,AF=
解方程 得
当 ,此时点 F 不在AC上.所以取
如图5,点F 在BC上,假设直线 EF 同时平分△ABC 的周长和面积,那么AE=x, BE =10-x,BF=12-(10-x)=2+x,EH= (10-x).
方程 整理,得 此方程无实数根.
10.满分解答
(1) 如图2,因为四边形ABCD 为正方形,所以∠BCD=90°.
因EF⊥BC,所以∠EFC=90°.所以EF ∥DC.
由平行线间的距离处处相等,得△EFD 与△EFC 为同底等高三角形.
所以△EFD 与△EFC 的面积相等.
(2)如图2,因为四边形 ABCD 为正方形,所以∠ACB=∠ACD =45°.
在Rt△ABC中,AB=BC=2,所以.
所以.
在Rt△EFC中, 设.EF=FC=m.
由勾股定理,得 整理,得
所以
所以
自变量的取值范围是(
(3) 分三种情况讨论△EDC 为等腰三角形.
①如图3,当CD=CE时,CE=2.所以.
②如图4,当EC=ED时,∠EDC=∠ECD=45°.所以∠ADE=45°.
所以 DE 为等腰直角三角形ADC 的角平分线.
由等腰三角形三线合一,
③如图5,当DC=DE时,∠DEC=∠ECD=45°.
此时点 E 与点A 重合,不符合题意,舍去.
11.满分解答
(1)如图2,由正方形ABCD,得AB=BC,∠ABC=∠C=90°.
所以
因为EG⊥AM,所以∠EGA=90°.
所以∠1+∠3=90°.
所以∠1=∠2.
在△ABM与△BCF中,∠1=∠2,AB=BC,∠ABC=∠C,所以△ABM≌△BCF.所以BM=CF.
(2)如图3,过点E作EH⊥DC 于H,得矩形 BCHE.
所以EH=BC=AB,CH=BE,∠EHF=90°.
由(1),得∠1=∠2.
在△ABM与△EHF 中,∠1=∠2,AB=EH,∠B=∠EHF,所以△ABM≌△EHF.
所以HF=BM=2.
因为BE=x,所以AE=4-x,DF=DC-CH-HF=2-x.
所以 ,定义域是0≤x<2.
12满分解答
(1) 因为四边形ABCD 是矩形,所以OA=OC, DA∥CB.
所以∠1=∠2.
在△AOE 和△COF 中,∠1=∠2,OA=OC,∠AOE=∠COF,所以△AOE≌△COF.所以OE=OF.
又因为EF⊥AC,所以四边形AFCE 是菱形.
(2)设菱形的边长为m.
在Rt△DEC中,EC=m,DE=x-m,DC=1,由勾股定理,得(
整理,得 解得
所以 定义域是x>0.
(3) 因为四边形ABCD 是矩形,所以OC=OD,∠5=∠6.
当△ODE 是等腰三角形时,分两种情况讨论.
①如图4,当点E 在线段AD 上时,△ODE 为钝角三角形,所以只可能存在EO=ED.此时,∠3=∠4.
因为∠ADC=90°,所以∠3+∠5=90°.
因为∠EOC=90°,所以∠4+∠7=90°.
根据等角的余角相等,得∠5=∠7.所以∠5=∠6=∠7=60°,∠3=30°.
在Rt△ADB 中,∠3=60°, AB=1,所以BD=2.所以.
②如图5,当点 E 在线段AD 的延长线上时,△ODE 为钝角三角形,所以只可能存在DO=DE.此时,∠8=∠4.
因为∠EDC=90°,所以∠8+∠EMD=90°.
因为∠EOC=90°,所以∠6+∠OMC=90°.
根据等角的余角相等,得. 所以 因为 所以 所以 在 中, 设 由勾股定理,得 解得 (不符合题意,舍去), 所以
13满分解答
(1) 如图3,过点D作DK ∥AC交BC 延长线于点K,得平行四边形ADKC.
所以AC=DK,AD=CK=x.
由等腰梯形的对角线相等,得AC=BD.所以BD=DK.
又AC⊥BD,所以∠BOC=90°.
所以∠BDK=90°,∠DBC=45°.
(2) 如图3,过点D 作DN⊥BC 于N,过点O作OH⊥BC 于H.
由(1),在等腰直角三角形DBK 中,
在等腰直角三角形OBC 中,
所以
所以 自变量的取值范围是x>0且x≠10.
(3) 如图4,过点A 作AM⊥BC 于M.
由(2),在 Rt△BND中, 所以
在 Rt△ABM中, 所以
在△ABC 中,PQ 是△ABC 的中位线,
在 Rt△AOB 中,OQ 是斜边上的中线,
在等腰直角三角形 BOC 中,
如图5,△OPQ 是等腰三角形,分三种情况讨论.
①当PQ=PO时, 解得 此时.
②当OQ=OP 时, 解得 (均不符合题意,舍去).
③当QO=QP 时, 解得x=0(不符号题意,舍去).
综上所述,如果△OPQ 是等腰三角形,
14.满分解答
(1) 如图2,因为四边形ABCD 是正方形,所以∠D=∠A =90°.
因为四边形 EFGH 是菱形,所以 HG=EH.
在 和 中,HG=EH,DG=AH=1,所以 所以∠1=∠2.
因为 所以 所以∠GHE=90°.
所以菱形 EFGH 为正方形.
(2) 如图3,过点 F 作DA 的平行线,交 DC 延长线于M.
所以
因为正方形ABCD 和菱形EFGH,所以HE=FG,DC∥AB,GF ∥HE.
所以 所以△HAE≌△FMG,MF=AH=1.
所以 定义域为0≤x≤
(3)过点G作GK⊥AB于K.
在Rt△DGH 中, 所以
在 中, 所以
在 中, 所以
所以 是等边三角形.所以.
15.满分解答
(1)如图2,过点A作AG⊥BC于G,过点D作DH⊥BC于H,得到矩形AGHD.
因为四边形ABCD为等腰梯形,所以∠C=∠B=60°,∠BAD=∠ADC=120°.
在Rt△ABG中,∠B=60°, AB=6cm,所以∠BAG=30°, BG=3cm,AG=3 cm.
同理可得,CH=3cm,BC=3+6+3=12cm.
所以
如图3,过点 D 作DM⊥AB 交BA 延长线于点M.
在Rt△ADM 中, 所以 因为BQ= tcm,所以AQ=(6-t) cm.
所以
所以
定义域是0
又因为∠ADC=∠2+∠3=120°,所以∠1=∠2.
在 和 中, 所以 所以 所以解得
16.满分解答
(1) 如图2,因为AD∥BC,所以∠CAD=∠ACB=30°.
在Rt△ACD 中,∠CAD=30°, AC=4,所以CD=2.
由勾股定理,得
如图3,因为MN 是梯形ABCD 的中位线,所以.
(2)如图4,在Rt△ACD中,AC=4,CD=x,由勾股定理,得. 所以 定义域是0
此时对角线BE=AC=4.
【方法一】如图5,过点 E 作AC 的平行线交BC 的延长线于点 H.所以四边形ACHE 是平行四边形.
所以AE=CH.根据等底等高的三角形面积相等,得S△ABE =S△ECH.
所以
因为BE⊥AC,所以BE⊥EH.
所以 是等腰直角三角形, 所以
【方法二】如图6,因为
所以
17.满分解答
(1) 如图2,作 DD'⊥BC于D'.
在Rt△DD'C中, 所以
所以.
(2)如图3,过点 F 作AB 的平行线交AD 的延长线于点A',交BC 于点B'.
在等腰直角三角形DA'F中,
在等腰直角三角形FB'C中,
过点 P 作PQ⊥EF 于Q, PQ交AD 于G,交BC 于H.
在等腰直角三角形 PEF 中,
在等腰直角三角形 PMN 中,
由GH=GQ+PQ+PH=8,得
整理,得y=-3x+10.定义域是
定义域是这样确定的:
当MN=y=0时,由-3x+10=0,得 (如图4所示).
当MN=y=AD=6时,由-3x+10=6,得 (如图5所示).
(3)MN=2存在两种情况:
① 如图6,当点 P 在梯形内部时, MN=2.
解方程-3x+10=2,得.
此时在梯形AEFD中,
所以梯形AEFD 的面积为
②如图7,当点 P 在梯形外部时, MN=2.
由GH=GQ+PQ-PH =8,得
整理,得y=3x-10.
解方程3x-10=2,得x=4.
此时在梯形AEFD中,AE=4,AD=6,EF=6+4=10.所以梯形AEFD的面积为32.
18满分解答
(1)如图2,在Rt△BCD中,BC=4,CD=4 ,所以BD=8,∠BDC=30°.
由△AED 和△ABD 是等高三角形,可得
因为 所以
定义域是0
如图4,作EN⊥AD于N,作EM⊥DC 于M.
在Rt△AEN 中, 所以
在Rt△EMC 中, 所以
因为AE=CE,所以.
所以 解得
(3)【方法一】① 如图5,当点 E 在OB 上时,由S△EOC =S△AOD,得S△EDC =S△ADC.
由△EDC 和△ADC 是同底三角形,所以高EM=AD=2.所以ED=4.
②如图6,当点 E 在OD 上时,此时 所以( 如图7,因为AD ∥BC,所以 又因为BD=8,所以 所以 所以
【方法二】① 当点 E 在OB 上时,如图8,设G、H 分别为OB、OC 的中点,那么GH 为△OBC 的中位线.
所以
所以∠ADO=∠HGO,∠DAO=∠GHO,AD=HG.
所以△AOD≌△HOG,所以S△AOD =S△HOG.
因为点 H 是OC 中点,所以S△co;=2S△HOG =2S△AOD.
所以当点 E为OG 中点时,
因为 所以
因为 所以
②如图6,当点 E 在OD 上时,
19满分解答
(1)如图2,因为∠1+∠3=90°,∠2+∠3=90°,所以∠1=∠2.又因为∠BFC=∠AOB=90°, BC=AB,所以△BFC≌△AOB.所以BF=AO=4,FC=OB=1.所以点C的坐标为(5,1).
(2)如图3,当A(0,4)、B(a,0)时,BF=AO=4,FC=OB=a,所以C(4+a,a).
因为CF ∥AO,所以四边形AOFC 是梯形.
因为E、G分别是AC、OF 的中点,所以EG 是梯形AOFC 的中位线.
所以
分两种情况求 S 关于a 的函数解析式,
①如图4,当B在G左侧时,(
此时
②如图5,当B在G右侧时, 此时
(3)①如图4,当B在G左侧,0
此时正方形 EHOG 的边长
③如图6,
由 得a=±2(舍去正值).此时EG=1.
④如图7,
由 得 (舍去正值).此时
同课章节目录
