四种命题的关系
图片预览



文档简介
课件9张PPT。四种命题的关系及真假 合肥一六八中学2009-11-11 观察下列四个命题:
(1)若f(x)是正弦函数,则f(x)是周期函数;
(2)若f(x)是周期函数,则f(x)是正弦函数;
(3)若f(x)不是正弦函数,则f(x)不是周期函数;
(4)若f(x)不是周期函数,则f(x)不是正弦函数;
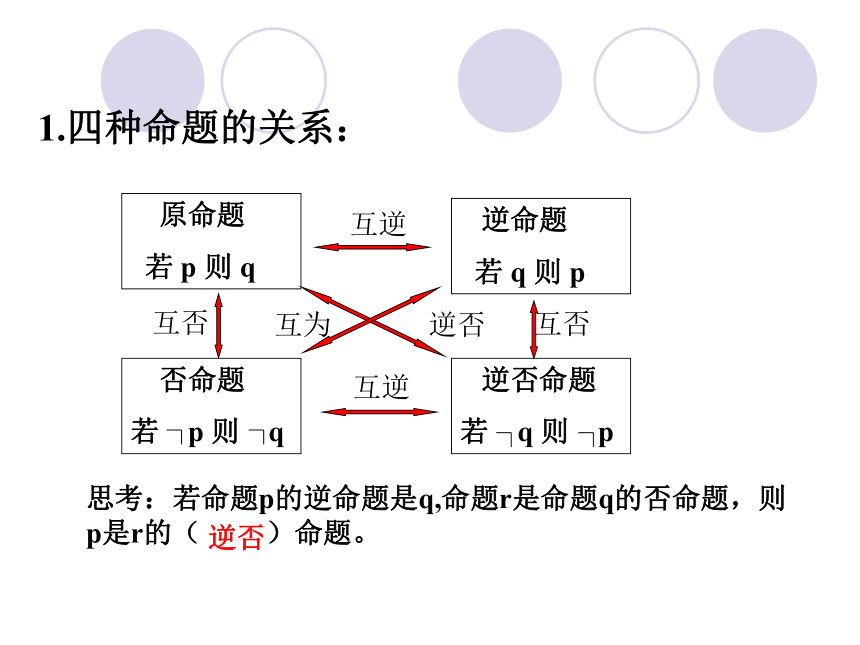
我们已经知道命题(1)与命题(2)(3)(4) 之间的关系。你能说出其中任意两个命题之间的相互关系吗?1.四种命题的关系: 原命题
若 p 则 q 逆命题
若 q 则 p互逆互逆互否互否互为逆否思考:若命题p的逆命题是q,命题r是命题q的否命题,则
p是r的( )命题。逆否2)原命题:若a=0, 则ab=0。逆命题:若ab=0, 则a=0。否命题:若a≠ 0, 则ab≠0。逆否命题:若ab≠0,则a≠0。(真)(假)(假)(真)(真)2.四种命题的真假关系看下面的例子:1)原命题:若x=2或x=3, 则x2-5x+6=0。逆命题:若x2-5x+6=0, 则x=2或x=3。否命题:若x≠2且x≠3, 则x2-5x+6≠0 。逆否命题:若x2-5x+6≠0,则x≠2且x≠3。(真)(真)(真)3) 原命题:若a > b, 则 ac2>bc2。逆命题:若ac2>bc2,则a>b。否命题:若a≤b,则ac2≤bc2。逆否命题:若ac2≤bc2,则a≤b。(假)(真)(真)(假)想一想?(2) 若其逆命题为真,则其否命题一定为真。但其原命题、
逆否命题不一定为真。
由以上三例及总结我们能发现什么?即:原命题与逆否命题的真假是等价的。逆命题与否命题的真假是等价的。(1) 原命题为真,则其逆否命题一定为真。但其逆命题、否
命题不一定为真。总结:练一练1.判断下列说法是否正确。1)一个命题的逆命题为真,它的逆否命题不一定为真;(对)2)一个命题的否命题为真,它的逆命题一定为真。(对)2.四种命题中真命题的个数可能为( )个。答:0个、2个、4个。如:原命题:若A∪B=A, 则A∩B=φ。逆命题:若A∩B=φ,则A∪B=A。否命题:若A∪B≠A,则A∩B≠φ。逆否命题:若A∩B≠φ,则A∪B≠A。(假)(假)(假)(假)3)一个命题的原命题为假,它的逆命题一定为假。(错)4)一个命题的逆否命题为假,它的否命题为假。(错)例题讲解例1:设原命题是:当c>0时,若a>b,则ac>bc. 写出它的逆命
题、否命题、逆否命题。并分别判断它们的真假。解:逆命题:当c>0时,若ac>bc, 则a>b.否命题:当c>0时,若a≤b, 则ac≤bc.逆否命题:当c>0时,若ac≤bc, 则a≤b.(真)(真)(真)分析:“当c>0时”是大前提,写其它命题时应该保留。原命题的条件是“a>b”,结论是“ac>bc”。
例2 若m≤0或n≤0,则m+n≤0。写出其逆命题、否命题、
逆否命题,并分别指出其真假。分析:搞清四种命题的定义及其关系,注意“且” “或”的
否定为“或” “且”。解:逆命题:若m+n≤0,则m≤0或n≤0。否命题:若m>0且n>0, 则m+n>0.逆否命题:若m+n>0, 则m>0且n>0.(真)(真)(假)小结:在判断四种命题的真假时,只需判断两种命题的
真假。因为逆命题与否命题真假等价,逆否命题与原命
题真假等价。原命题
若p则q否命题
若┐p则┐q逆否命题
若┐q则┐p逆命题
若q则p互
否互 逆互 逆互
否互 为互 为逆 否逆 否小结
(1)若f(x)是正弦函数,则f(x)是周期函数;
(2)若f(x)是周期函数,则f(x)是正弦函数;
(3)若f(x)不是正弦函数,则f(x)不是周期函数;
(4)若f(x)不是周期函数,则f(x)不是正弦函数;
我们已经知道命题(1)与命题(2)(3)(4) 之间的关系。你能说出其中任意两个命题之间的相互关系吗?1.四种命题的关系: 原命题
若 p 则 q 逆命题
若 q 则 p互逆互逆互否互否互为逆否思考:若命题p的逆命题是q,命题r是命题q的否命题,则
p是r的( )命题。逆否2)原命题:若a=0, 则ab=0。逆命题:若ab=0, 则a=0。否命题:若a≠ 0, 则ab≠0。逆否命题:若ab≠0,则a≠0。(真)(假)(假)(真)(真)2.四种命题的真假关系看下面的例子:1)原命题:若x=2或x=3, 则x2-5x+6=0。逆命题:若x2-5x+6=0, 则x=2或x=3。否命题:若x≠2且x≠3, 则x2-5x+6≠0 。逆否命题:若x2-5x+6≠0,则x≠2且x≠3。(真)(真)(真)3) 原命题:若a > b, 则 ac2>bc2。逆命题:若ac2>bc2,则a>b。否命题:若a≤b,则ac2≤bc2。逆否命题:若ac2≤bc2,则a≤b。(假)(真)(真)(假)想一想?(2) 若其逆命题为真,则其否命题一定为真。但其原命题、
逆否命题不一定为真。
由以上三例及总结我们能发现什么?即:原命题与逆否命题的真假是等价的。逆命题与否命题的真假是等价的。(1) 原命题为真,则其逆否命题一定为真。但其逆命题、否
命题不一定为真。总结:练一练1.判断下列说法是否正确。1)一个命题的逆命题为真,它的逆否命题不一定为真;(对)2)一个命题的否命题为真,它的逆命题一定为真。(对)2.四种命题中真命题的个数可能为( )个。答:0个、2个、4个。如:原命题:若A∪B=A, 则A∩B=φ。逆命题:若A∩B=φ,则A∪B=A。否命题:若A∪B≠A,则A∩B≠φ。逆否命题:若A∩B≠φ,则A∪B≠A。(假)(假)(假)(假)3)一个命题的原命题为假,它的逆命题一定为假。(错)4)一个命题的逆否命题为假,它的否命题为假。(错)例题讲解例1:设原命题是:当c>0时,若a>b,则ac>bc. 写出它的逆命
题、否命题、逆否命题。并分别判断它们的真假。解:逆命题:当c>0时,若ac>bc, 则a>b.否命题:当c>0时,若a≤b, 则ac≤bc.逆否命题:当c>0时,若ac≤bc, 则a≤b.(真)(真)(真)分析:“当c>0时”是大前提,写其它命题时应该保留。原命题的条件是“a>b”,结论是“ac>bc”。
例2 若m≤0或n≤0,则m+n≤0。写出其逆命题、否命题、
逆否命题,并分别指出其真假。分析:搞清四种命题的定义及其关系,注意“且” “或”的
否定为“或” “且”。解:逆命题:若m+n≤0,则m≤0或n≤0。否命题:若m>0且n>0, 则m+n>0.逆否命题:若m+n>0, 则m>0且n>0.(真)(真)(假)小结:在判断四种命题的真假时,只需判断两种命题的
真假。因为逆命题与否命题真假等价,逆否命题与原命
题真假等价。原命题
若p则q否命题
若┐p则┐q逆否命题
若┐q则┐p逆命题
若q则p互
否互 逆互 逆互
否互 为互 为逆 否逆 否小结
