2024-2025学年上海浦外附中高二上学期数学期中试卷(含答案)(2024.11)
文档属性
| 名称 | 2024-2025学年上海浦外附中高二上学期数学期中试卷(含答案)(2024.11) | 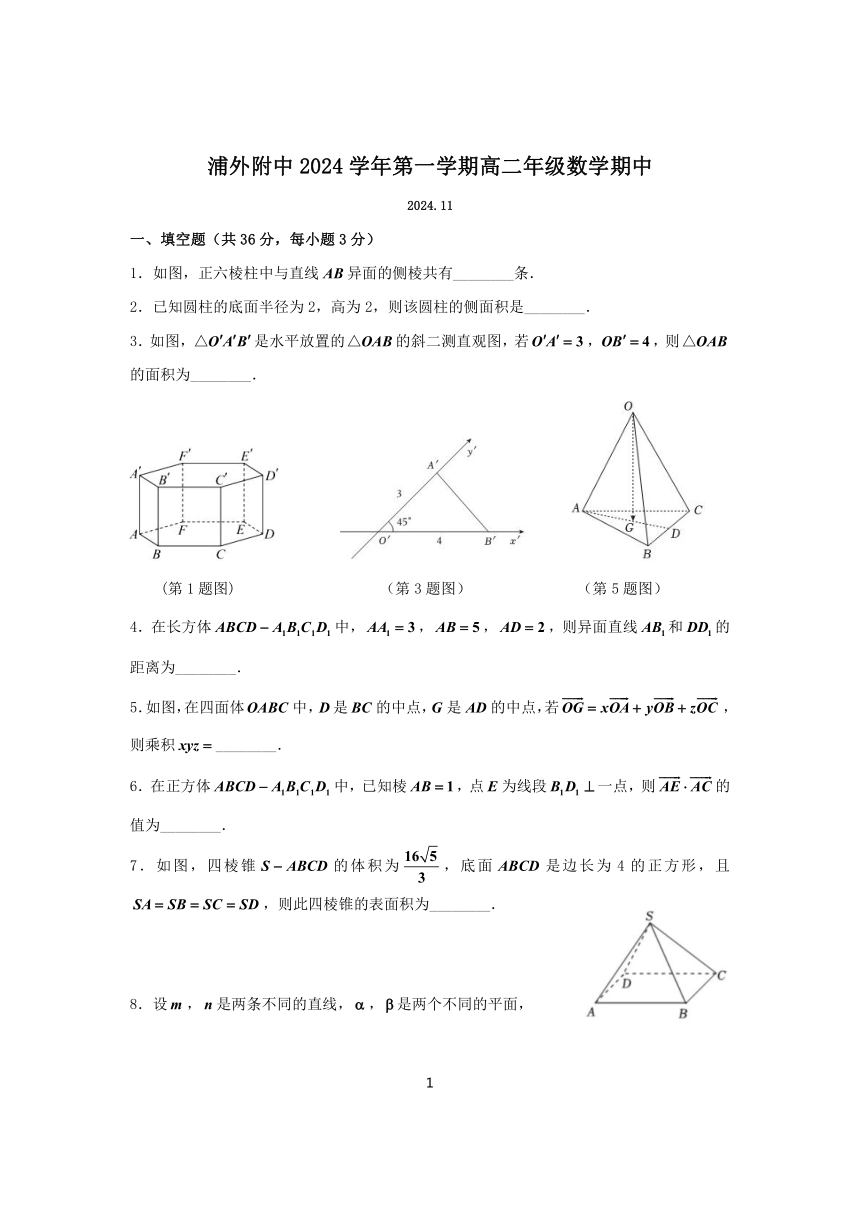 | |
| 格式 | docx | ||
| 文件大小 | 838.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-30 20:49:19 | ||
图片预览





文档简介
浦外附中2024学年第一学期高二年级数学期中
2024.11
一、填空题(共36分,每小题3分)
1.如图,正六棱柱中与直线异面的侧棱共有________条.
2.已知圆柱的底面半径为2,高为2,则该圆柱的侧面积是________.
3.如图,是水平放置的的斜二测直观图,若,,则的面积为________.
(第1题图) (第3题图) (第5题图)
4.在长方体中,,,,则异面直线和的距离为________.
5.如图,在四面体中,是的中点,是的中点,若,则乘积________.
6.在正方体中,已知棱,点为线段一点,则的值为________.
7.如图,四棱锥的体积为,底面是边长为4的正方形,且,则此四棱锥的表面积为________.
8.设,是两条不同的直线,,是两个不同的平面,
(1)若,,,则;(2)若,,,则;
(3)若,,,则;(4)若,,,则
其中正确的命题有________.(填写所有正确命题的编号)
9.如图,正四棱柱的底面边长为2,,为的中点,则到平面的距离为________.
10.如图所示,绕直角边所在直线旋转一周形成一个圆锥,已知在空间直角坐标系中,点和点均在圆锥的母线上,则圆锥的表面积为________.
(第9题图) (第10题图) (第11题图)
11.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有升水时,水面恰好经过正四棱锥的顶点.如果将容器倒置,水面也恰好经过点(图2),试正四棱柱的高为,正四棱锥的高为,则________.
12.如图,在直四棱柱中,底面为平行四边形,,,,,点在上底面所在平面上,使得,点在下底面所在平面上,使得,若三棱锥的外接球表面积为,则的取值范围是________.
二、单选题(共12分,每小题3分)
13.已知直线平面,则“直线”是“”的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
14.以下说法正确的是( )
A.各侧面都是矩形的棱柱是长方体
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.各侧面都是全等的等腰三角形的四棱锥是正四棱锥
D.底面四条边相等的直棱柱是正四棱柱
15.已知是棱长为1的正四面体.若点满足,其中,则的最小值为( )
A. B.1 C.0 D.
16.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼.营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱,中间是球的一部分(除去两个球缺).如图2.“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为,其中是球的半径,是球缺的高.已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则该灯笼的体积为(取)( )
A. B. C. D.
三、解答题(共52分)
17.(本题满分8分,)如图,在三棱柱中,侧面,均为正方形,,,点是棱的中点.
(1)求证:平面;
(2)求异面直线与所成角的大小.
18.(本题满分8分,)已知空间三点,,.
(1)若向量与互相垂直,求实数的值;
(2)求以,为邻边的平行四边形的面积.
19.(本题满分10分,)如图,圆柱中,是一条母线,是底面一条直径,是的中点.
(1)证明:平面平面;
(2)若,求二面角的余弦值.
20.(本题满分11分,)如图1,在中,,,为的中点,现将及其内部以边为轴进行旋转,得到如图2所示的新的几何体,点为旋转过程中形成的圆的圆心,为圆上任意一点.
(1)求新的几何体的体积;
(2)记与底面所成角为,求的取值范围.
21.(本题满分15分,)如图在四面体中,是边长为2的等边三角形,为直角三角形,其中为直角顶点,,、、、分别是线段、、、上的动点,且四边形为平行四边形.
(1)求证:平面;
(2)试探究当二面角从增加到的过程中,线段在平面上的投影所扫过的平面区域的面积;
(3)设,且是以为底的等腰三角形,当为何值时,多面体的体积恰好为?
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.;
10.; 11.; 12.;
11.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有升水时,水面恰好经过正四棱锥的顶点.如果将容器倒置,水面也恰好经过点(图2),试正四棱柱的高为,正四棱锥的高为,则________.
【答案】
【解析】设图(1)中到正四棱柱下底面与上底面的距离分别为,正四棱柱的上下底面面积为,则由图(1)可得,
又由图(2)可得
正四棱柱的高为,正四棱柱的高为故答案为:.
12.如图,在直四棱柱中,底面为平行四边形,,,,,点在上底面所在平面上,使得,点在下底面所在平面上,使得,若三棱锥的外接球表面积为,则的取值范围是________.
【答案】
【解析】在中,已知,
则,可得,
取的中点分别为,则
由,得点在平面的轨迹为以为直径的圆,记为.
又,得点在平面的轨迹为以为直径的圆,记为,
可得经过点,且三棱锥的外接球球心在直线上.
设,球的半径为,
在中,由勾股定理得:
在中,由勾股定理得:
联立(1)(2)可得,由,得,
则,可得三棱锥的外接球的表面积.
故答案为:.
二、选择题
13.B; 14.B; 15.A; 16.A
15.已知是棱长为1的正四面体.若点满足,其中,则的最小值为( )
A. B.1 C.0 D.
【答案】A
【解析】根据题意,点满足,其中
所以,可得,因为点是平面内的一点,又正四面体棱长为1,
所以当点与在上的射影重合时,等于正四面体的高,
此时且达到最小值。故答案为:.故选A.
16.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼.营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱,中间是球的一部分(除去两个球缺).如图2.“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为,其中是球的半径,是球缺的高.已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则该灯笼的体积为(取)( )
A. B. C. D.
【答案】A
【解析】由题意得,解得,
所以两个球缺的体积之和为
因为取,所以,所以中间部分的体积为
因为上下两个圆柱的体积之和为
所以围成该灯笼的体积为.故选A.
三、解答题
17.(1)证明略 (2)
18.(1) (2)
19.(1)证明略 (2)
20.如图1,在中,,,为的中点,现将及其内部以边为轴进行旋转,得到如图2所示的新的几何体,点为旋转过程中形成的圆的圆心,为圆上任意一点.
(1)求新的几何体的体积;
(2)记与底面所成角为,求的取值范围.
【答案】(1) (2)
【解析】(1)连接,由题可得
所以新的几何体的体积
(2)如图,作的中点,连接,易知为与底面所面的角,则,又因为,所以.
21.如图在四面体中,是边长为2的等边三角形,为直角三角形,其中为直角顶点,,、、、分别是线段、、、上的动点,且四边形为平行四边形.
(1)求证:平面;
(2)试探究当二面角从增加到的过程中,线段在平面上的投影所扫过的平面区域的面积;
(3)设,且是以为底的等腰三角形,当为何值时,多面体的体积恰好为?
【答案】(1)见解析 (2) (3)
【解析】(1)证明:四边形为平行四边形,.
而面面,面.
而面,面面,.
而面面,面.
(2),在平面上的投影满足,即在线段的中垂线上.
如右图所示,将补成边长为2的正,
当二面角为角时,即点在平面上,
此时为,当二面角为角时,此时为中点,
故在平面上的投影所扫过的平面区域为,
而,故线段在平面上的投影所扫过的平面区域的面积为.
(3),且为等腰三角形,.
取中点,由题意得:,,
满足,根据勾股定理可知.
平面
而多面体的体积恰好为
即多面体的体积恰为四面体体积的一半.连接
.,整理得解得.
2024.11
一、填空题(共36分,每小题3分)
1.如图,正六棱柱中与直线异面的侧棱共有________条.
2.已知圆柱的底面半径为2,高为2,则该圆柱的侧面积是________.
3.如图,是水平放置的的斜二测直观图,若,,则的面积为________.
(第1题图) (第3题图) (第5题图)
4.在长方体中,,,,则异面直线和的距离为________.
5.如图,在四面体中,是的中点,是的中点,若,则乘积________.
6.在正方体中,已知棱,点为线段一点,则的值为________.
7.如图,四棱锥的体积为,底面是边长为4的正方形,且,则此四棱锥的表面积为________.
8.设,是两条不同的直线,,是两个不同的平面,
(1)若,,,则;(2)若,,,则;
(3)若,,,则;(4)若,,,则
其中正确的命题有________.(填写所有正确命题的编号)
9.如图,正四棱柱的底面边长为2,,为的中点,则到平面的距离为________.
10.如图所示,绕直角边所在直线旋转一周形成一个圆锥,已知在空间直角坐标系中,点和点均在圆锥的母线上,则圆锥的表面积为________.
(第9题图) (第10题图) (第11题图)
11.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有升水时,水面恰好经过正四棱锥的顶点.如果将容器倒置,水面也恰好经过点(图2),试正四棱柱的高为,正四棱锥的高为,则________.
12.如图,在直四棱柱中,底面为平行四边形,,,,,点在上底面所在平面上,使得,点在下底面所在平面上,使得,若三棱锥的外接球表面积为,则的取值范围是________.
二、单选题(共12分,每小题3分)
13.已知直线平面,则“直线”是“”的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
14.以下说法正确的是( )
A.各侧面都是矩形的棱柱是长方体
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.各侧面都是全等的等腰三角形的四棱锥是正四棱锥
D.底面四条边相等的直棱柱是正四棱柱
15.已知是棱长为1的正四面体.若点满足,其中,则的最小值为( )
A. B.1 C.0 D.
16.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼.营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱,中间是球的一部分(除去两个球缺).如图2.“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为,其中是球的半径,是球缺的高.已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则该灯笼的体积为(取)( )
A. B. C. D.
三、解答题(共52分)
17.(本题满分8分,)如图,在三棱柱中,侧面,均为正方形,,,点是棱的中点.
(1)求证:平面;
(2)求异面直线与所成角的大小.
18.(本题满分8分,)已知空间三点,,.
(1)若向量与互相垂直,求实数的值;
(2)求以,为邻边的平行四边形的面积.
19.(本题满分10分,)如图,圆柱中,是一条母线,是底面一条直径,是的中点.
(1)证明:平面平面;
(2)若,求二面角的余弦值.
20.(本题满分11分,)如图1,在中,,,为的中点,现将及其内部以边为轴进行旋转,得到如图2所示的新的几何体,点为旋转过程中形成的圆的圆心,为圆上任意一点.
(1)求新的几何体的体积;
(2)记与底面所成角为,求的取值范围.
21.(本题满分15分,)如图在四面体中,是边长为2的等边三角形,为直角三角形,其中为直角顶点,,、、、分别是线段、、、上的动点,且四边形为平行四边形.
(1)求证:平面;
(2)试探究当二面角从增加到的过程中,线段在平面上的投影所扫过的平面区域的面积;
(3)设,且是以为底的等腰三角形,当为何值时,多面体的体积恰好为?
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.;
10.; 11.; 12.;
11.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有升水时,水面恰好经过正四棱锥的顶点.如果将容器倒置,水面也恰好经过点(图2),试正四棱柱的高为,正四棱锥的高为,则________.
【答案】
【解析】设图(1)中到正四棱柱下底面与上底面的距离分别为,正四棱柱的上下底面面积为,则由图(1)可得,
又由图(2)可得
正四棱柱的高为,正四棱柱的高为故答案为:.
12.如图,在直四棱柱中,底面为平行四边形,,,,,点在上底面所在平面上,使得,点在下底面所在平面上,使得,若三棱锥的外接球表面积为,则的取值范围是________.
【答案】
【解析】在中,已知,
则,可得,
取的中点分别为,则
由,得点在平面的轨迹为以为直径的圆,记为.
又,得点在平面的轨迹为以为直径的圆,记为,
可得经过点,且三棱锥的外接球球心在直线上.
设,球的半径为,
在中,由勾股定理得:
在中,由勾股定理得:
联立(1)(2)可得,由,得,
则,可得三棱锥的外接球的表面积.
故答案为:.
二、选择题
13.B; 14.B; 15.A; 16.A
15.已知是棱长为1的正四面体.若点满足,其中,则的最小值为( )
A. B.1 C.0 D.
【答案】A
【解析】根据题意,点满足,其中
所以,可得,因为点是平面内的一点,又正四面体棱长为1,
所以当点与在上的射影重合时,等于正四面体的高,
此时且达到最小值。故答案为:.故选A.
16.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼.营造一种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱,中间是球的一部分(除去两个球缺).如图2.“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为,其中是球的半径,是球缺的高.已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则该灯笼的体积为(取)( )
A. B. C. D.
【答案】A
【解析】由题意得,解得,
所以两个球缺的体积之和为
因为取,所以,所以中间部分的体积为
因为上下两个圆柱的体积之和为
所以围成该灯笼的体积为.故选A.
三、解答题
17.(1)证明略 (2)
18.(1) (2)
19.(1)证明略 (2)
20.如图1,在中,,,为的中点,现将及其内部以边为轴进行旋转,得到如图2所示的新的几何体,点为旋转过程中形成的圆的圆心,为圆上任意一点.
(1)求新的几何体的体积;
(2)记与底面所成角为,求的取值范围.
【答案】(1) (2)
【解析】(1)连接,由题可得
所以新的几何体的体积
(2)如图,作的中点,连接,易知为与底面所面的角,则,又因为,所以.
21.如图在四面体中,是边长为2的等边三角形,为直角三角形,其中为直角顶点,,、、、分别是线段、、、上的动点,且四边形为平行四边形.
(1)求证:平面;
(2)试探究当二面角从增加到的过程中,线段在平面上的投影所扫过的平面区域的面积;
(3)设,且是以为底的等腰三角形,当为何值时,多面体的体积恰好为?
【答案】(1)见解析 (2) (3)
【解析】(1)证明:四边形为平行四边形,.
而面面,面.
而面,面面,.
而面面,面.
(2),在平面上的投影满足,即在线段的中垂线上.
如右图所示,将补成边长为2的正,
当二面角为角时,即点在平面上,
此时为,当二面角为角时,此时为中点,
故在平面上的投影所扫过的平面区域为,
而,故线段在平面上的投影所扫过的平面区域的面积为.
(3),且为等腰三角形,.
取中点,由题意得:,,
满足,根据勾股定理可知.
平面
而多面体的体积恰好为
即多面体的体积恰为四面体体积的一半.连接
.,整理得解得.
同课章节目录
