2.1.2由曲线求它的方程,由方程研究曲线的性质
文档属性
| 名称 | 2.1.2由曲线求它的方程,由方程研究曲线的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 150.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-13 10:26:48 | ||
图片预览








文档简介
课件23张PPT。中国人民大学附属中学2.1.2由曲线求它的方程,
由方程研究曲线的性质 在研究直线与圆的方程时,我们已经看到解析几何主要推论下面两个基本问题:
1.由曲线求它的方程;
2.利用方程研究曲线的性质. 下面让我们通过实例,进一步体会如何建立曲线的方程,以及如何利用方程以及曲线的性质。例1.设动点M与两条互相垂直的直线的距离的积等于1,求动点M的轨迹方程并利用方程研究轨迹(曲线)的性质。解:(1)求动点M的轨迹方程:① 建立直角坐标系. 取已知两条互相垂直的直线为坐标轴,建立平面直角坐标系xOy;② 设动点M的坐标为(x,y); ③ 把几何条件转化为坐标表示:
过点M分别作x轴,y轴的垂线,垂足分别为E,F,有轨迹上的点M与两坐标轴的距离之积等于1,得 因为点M与x轴的距离|ME|=|y|,与y轴的距离|MF|=|x|,所以上述条件转化为方程的表示:|x|·|y|=1. 这个方程等价于xy=1或xy=-1. 这就是说,M(x,y)在曲线上,则它的坐标满足方程,以|x|·|y|=1的解为坐标的点M(x,y)都在曲线上。因此方程|x|·|y|=1为所求动点轨迹的方程.④ 证明(略);(2)利用方程研究曲线的性质:① 曲线的组成 由于方程|x|·|y|=1等价于下列两个方程xy=1或xy=-1,每一个方程都表示一条曲线,由此可知表示方程的曲线由上述两个方程的曲线组成;② 曲线与坐标轴的交点 由方程|x|·|y|=1,可推知x≠0且y≠0,因此方程的曲线与两坐标轴没有交点,方程对应的曲线被两条坐标轴分开;③ 曲线的对称性质 在方程|x|·|y|=1中,以-x代替x,这个方程并未变化,因此方程的图象关于y轴对称. 在方程|x|·|y|=1中,以-y代替y,这个方程也未变化,因此方程的图象关于x轴对称;
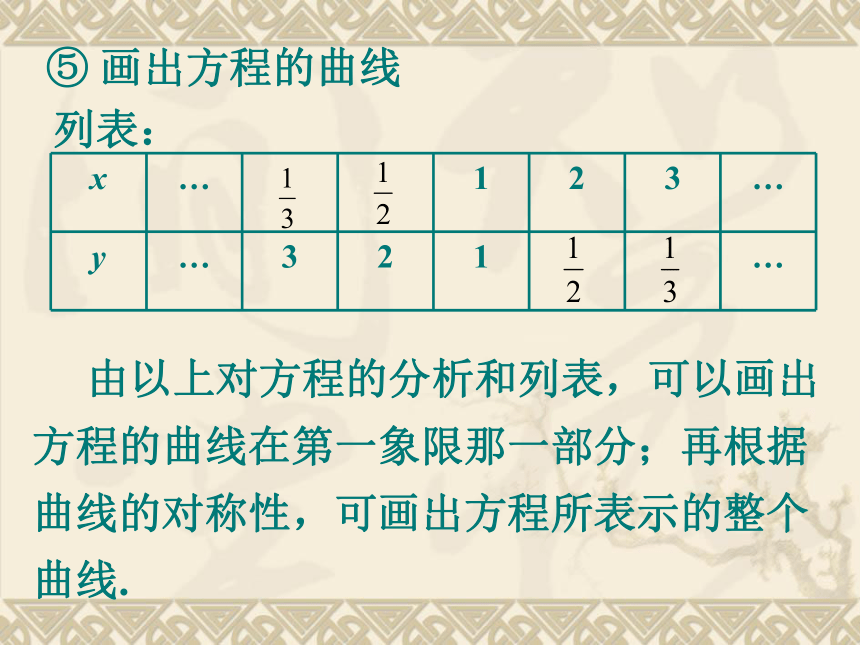
在方程|x|·|y|=1中,以-x代替x,同时以-y代替y,这个方程也未变化,因此方程的图象关于原点中心对称. 由以上分析可知,这个方程所表示的曲线,既是轴对称图形,也是中心对称图形。因此在我们研究方程的曲线时,只要研究它在第一象限那一部分曲线即可;④ 曲线的变化情况 由曲线的对称性质,我们只考虑第一象限的情况(x>0,y>0),由方程可知,当变量x逐渐变大时,变量y的值逐渐变小,曲线无限地靠近x轴;当变量x逐渐变小时,变量y的值逐渐变大,曲线无限地靠近y轴;⑤ 画出方程的曲线列表: 由以上对方程的分析和列表,可以画出方程的曲线在第一象限那一部分;再根据曲线的对称性,可画出方程所表示的整个曲线.例2.已知一曲线在x轴的上方,它上面的每一个点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程。解:设曲线上任一点的坐标为M(x,y), 作MB⊥x轴,B为垂足,则点M属于集合P={M| |MA|-|MB|=2},由距离公式,点M适合的条件可表示为化简为x2=8y, 因为曲线在x轴的上方,所以 y>0,显然(0,0)是这个方程的解,但不属于已知曲线,
所以曲线的方程是x2=8y (y≠0).例3.已知平面上两个定点A、B之间的距离为2a,点M到A、B两点的距离之比为2:1,求动点M的轨迹方程。解:以两定点A、B所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,
由AB=2a,可设A(-a,0),B(a,0),M(x,y), ∴ ∵ |MA|:|MB|=2:1, 化简得 所以动点M的轨迹方程为 例4.画出方程y2-4x-4=0的曲线。解:(1)范围:∵ y2=4x+4≥0,
得x≥-1,y可取一切实数,所以曲线在直线x=-1的右侧,向上向下无限延伸;(2)对称性:用-y代替y,方程不变,故曲线关于x轴对称;(3)截距:令y=0,得x=-1,令x=0,得y=±2;即曲线的横截距为-1,纵截距为±2;(4)列表:(5)描点作图.课堂练习1.到A(2,-3)和B(4,-1)的距离相等的点的轨迹方程是( )
(A)x-y-1=0
(B)x-y+1=0
(C)x+y-1=0
(D)x+y+1=0C2.直角坐标系内到两坐标轴距离之差等于1的点的轨迹方程是( )
(A)|x|-|y|=1
(B)|x-y|=1
(C)|x|-|y|=±1
(D)|x±y|=1C3.已知点M(-2,0)、N(2,0),则以MN为斜边的直角三角形的直角顶点的轨迹方程是( )
(A)x2+y2=4 (x≠±2)
(B)x2+y2=4
(C)x2+y2=16
(D)x2+y2=16 (x≠±4)A4.方程 所表示的图形是( )
(A)x2=y的图形在第二象限的部分 (B)与x2=y的图形相同
(C)与x2=-y的图形相同
(D)x2=-y的图形在第四象限的部分A5.方程(x+a)(y-a)=0表示的曲线是( )
(A)两条相交的直线
(B)一个点(-a,a)
(C)与方程组 的图形相同
(D)第一、三象限的角平分线A6.已知A(-1,0),B(2,4),△ABC的面积为10,求动点C的轨迹方程。4x-3y-16=0或4x-3y+24=07.已知点M到点F(0,1)和直线l:y=-1的距离相等,求点M的轨迹方程。8.已知△ABC的顶点B(0,0),C(5,0),AB边上的中线长|CD|=3,求顶点A的轨迹方程。 x2+y2-20x+64=0 (y≠0)
1.由曲线求它的方程;
2.利用方程研究曲线的性质. 下面让我们通过实例,进一步体会如何建立曲线的方程,以及如何利用方程以及曲线的性质。例1.设动点M与两条互相垂直的直线的距离的积等于1,求动点M的轨迹方程并利用方程研究轨迹(曲线)的性质。解:(1)求动点M的轨迹方程:① 建立直角坐标系. 取已知两条互相垂直的直线为坐标轴,建立平面直角坐标系xOy;② 设动点M的坐标为(x,y); ③ 把几何条件转化为坐标表示:
过点M分别作x轴,y轴的垂线,垂足分别为E,F,有轨迹上的点M与两坐标轴的距离之积等于1,得 因为点M与x轴的距离|ME|=|y|,与y轴的距离|MF|=|x|,所以上述条件转化为方程的表示:|x|·|y|=1. 这个方程等价于xy=1或xy=-1. 这就是说,M(x,y)在曲线上,则它的坐标满足方程,以|x|·|y|=1的解为坐标的点M(x,y)都在曲线上。因此方程|x|·|y|=1为所求动点轨迹的方程.④ 证明(略);(2)利用方程研究曲线的性质:① 曲线的组成 由于方程|x|·|y|=1等价于下列两个方程xy=1或xy=-1,每一个方程都表示一条曲线,由此可知表示方程的曲线由上述两个方程的曲线组成;② 曲线与坐标轴的交点 由方程|x|·|y|=1,可推知x≠0且y≠0,因此方程的曲线与两坐标轴没有交点,方程对应的曲线被两条坐标轴分开;③ 曲线的对称性质 在方程|x|·|y|=1中,以-x代替x,这个方程并未变化,因此方程的图象关于y轴对称. 在方程|x|·|y|=1中,以-y代替y,这个方程也未变化,因此方程的图象关于x轴对称;
在方程|x|·|y|=1中,以-x代替x,同时以-y代替y,这个方程也未变化,因此方程的图象关于原点中心对称. 由以上分析可知,这个方程所表示的曲线,既是轴对称图形,也是中心对称图形。因此在我们研究方程的曲线时,只要研究它在第一象限那一部分曲线即可;④ 曲线的变化情况 由曲线的对称性质,我们只考虑第一象限的情况(x>0,y>0),由方程可知,当变量x逐渐变大时,变量y的值逐渐变小,曲线无限地靠近x轴;当变量x逐渐变小时,变量y的值逐渐变大,曲线无限地靠近y轴;⑤ 画出方程的曲线列表: 由以上对方程的分析和列表,可以画出方程的曲线在第一象限那一部分;再根据曲线的对称性,可画出方程所表示的整个曲线.例2.已知一曲线在x轴的上方,它上面的每一个点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程。解:设曲线上任一点的坐标为M(x,y), 作MB⊥x轴,B为垂足,则点M属于集合P={M| |MA|-|MB|=2},由距离公式,点M适合的条件可表示为化简为x2=8y, 因为曲线在x轴的上方,所以 y>0,显然(0,0)是这个方程的解,但不属于已知曲线,
所以曲线的方程是x2=8y (y≠0).例3.已知平面上两个定点A、B之间的距离为2a,点M到A、B两点的距离之比为2:1,求动点M的轨迹方程。解:以两定点A、B所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,
由AB=2a,可设A(-a,0),B(a,0),M(x,y), ∴ ∵ |MA|:|MB|=2:1, 化简得 所以动点M的轨迹方程为 例4.画出方程y2-4x-4=0的曲线。解:(1)范围:∵ y2=4x+4≥0,
得x≥-1,y可取一切实数,所以曲线在直线x=-1的右侧,向上向下无限延伸;(2)对称性:用-y代替y,方程不变,故曲线关于x轴对称;(3)截距:令y=0,得x=-1,令x=0,得y=±2;即曲线的横截距为-1,纵截距为±2;(4)列表:(5)描点作图.课堂练习1.到A(2,-3)和B(4,-1)的距离相等的点的轨迹方程是( )
(A)x-y-1=0
(B)x-y+1=0
(C)x+y-1=0
(D)x+y+1=0C2.直角坐标系内到两坐标轴距离之差等于1的点的轨迹方程是( )
(A)|x|-|y|=1
(B)|x-y|=1
(C)|x|-|y|=±1
(D)|x±y|=1C3.已知点M(-2,0)、N(2,0),则以MN为斜边的直角三角形的直角顶点的轨迹方程是( )
(A)x2+y2=4 (x≠±2)
(B)x2+y2=4
(C)x2+y2=16
(D)x2+y2=16 (x≠±4)A4.方程 所表示的图形是( )
(A)x2=y的图形在第二象限的部分 (B)与x2=y的图形相同
(C)与x2=-y的图形相同
(D)x2=-y的图形在第四象限的部分A5.方程(x+a)(y-a)=0表示的曲线是( )
(A)两条相交的直线
(B)一个点(-a,a)
(C)与方程组 的图形相同
(D)第一、三象限的角平分线A6.已知A(-1,0),B(2,4),△ABC的面积为10,求动点C的轨迹方程。4x-3y-16=0或4x-3y+24=07.已知点M到点F(0,1)和直线l:y=-1的距离相等,求点M的轨迹方程。8.已知△ABC的顶点B(0,0),C(5,0),AB边上的中线长|CD|=3,求顶点A的轨迹方程。 x2+y2-20x+64=0 (y≠0)
