2.2.1椭圆的标准方程
文档属性
| 名称 | 2.2.1椭圆的标准方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-13 00:00:00 | ||
图片预览







文档简介
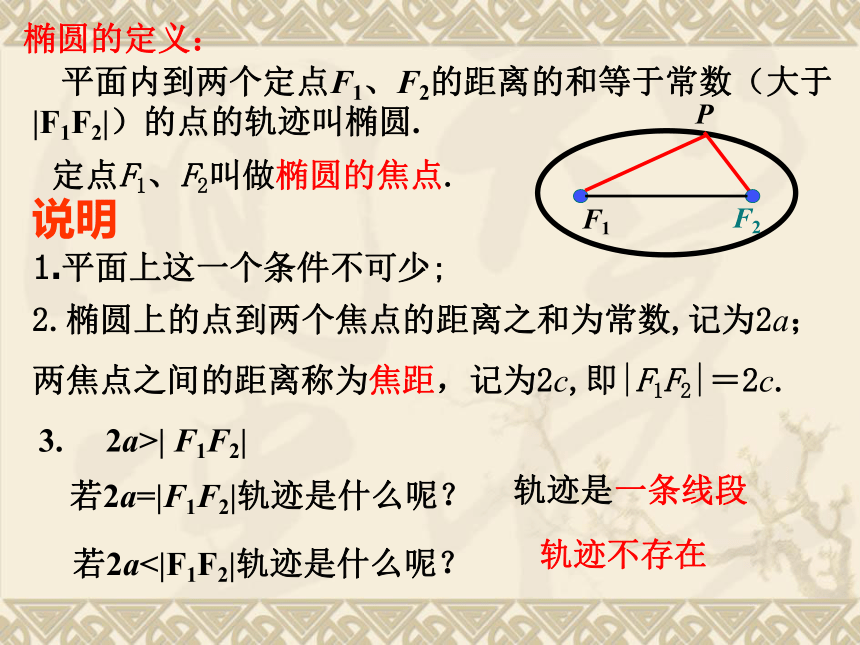
课件28张PPT。中国人民大学附属中学2.2.1椭圆的标准方程 平面内到两个定点F1、F2的距离的和等于常数(大于
|F1F2|)的点的轨迹叫椭圆.定点F1、F2叫做椭圆的焦点.2.椭圆上的点到两个焦点的距离之和为常数,记为2a;
两焦点之间的距离称为焦距,记为2c,即|F1F2|=2c.说明椭圆的定义:1.平面上这一个条件不可少;3. 2a>| F1F2|若2a=|F1F2|轨迹是什么呢?若2a<|F1F2|轨迹是什么呢?轨迹是一条线段轨迹不存在怎样推导椭圆的方程:求曲线方程的一般步骤是什么?如何建立适当的直角坐标系?原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)? 探讨建立平面直角坐标系的方案方案一(对称、“简洁”) 以过焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy,这时F1,F2的坐标分别为(-c,0),(c,0), 设M(x,y)是椭圆上的任意一点,根据椭圆的定义可知,点M在椭圆上的充分必要条件是|MF1|+|MF2|=2a,因为
所以上述条件转化为坐标表示,就是 ① 当x≠0时, 由①得 整理得 即 ② ①+②,整理得 ③ 将③式平方,再整理得 ④ 因为a>c>0,所以a2-c2>0,设a2-c2=b2>0,则④式化为 ⑤ 当x=0时,|MF1|=|MF2|=a,由 得y2=a2-c2=b2,此时M的坐标适合⑤. 因此,方程⑤是给定的椭圆的方程。
通常把这个方程叫做椭圆的标准方程。
焦点是F1(-c,0),F2(c,0),且c2=a2-b2.思考:如果椭圆的焦点在y轴上, 焦点是F1(0,-c),F2(0,c),只要将方程①的x,y互换,就可以得到它的方程,
其中b2=a2-c2,这个方程也是椭圆的标准方程。例1. 求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-3,0),(3,0),椭圆上任意一点与两焦点的距离的和等于8;解:(1)椭圆的焦点在x轴上,设它的标准方程是由已知,得2a=8,即a=4,又因为c=3,
所以b2=a2-c2=7,因此椭圆的标准方程是 解:(2)椭圆的焦点在y轴上,设它的标准方程是 由已知,得c=4,因为c2=a2-b2,
所以a2=b2+16 ①将①代入②得, 解得b2=4 (b2=-12舍去),则a2=4+16=20,因此椭圆的标准方程是 解:(1)已知方程就是椭圆的标准方程,由36>24,可知这个椭圆的焦点在x轴上,且a2=36,b2=24,所以c2=a2-b2=12, 解:(2)把已知方程化为标准方程,
由8>3可知这个椭圆的解得在y轴上,
且a2=8,b2=3,得c2=a2-b2=5,(2)8x2+3y2=24.例3. 已知B,C是两个定点,|BC|=8,且△ABC的周长等于18,求这个三角形的顶点A的轨迹方程。解:以过B,C两点的直线为x轴,线段BC的垂直平分线为y轴,建立直角坐标系xOy,
由|BC|=8,可知B(-4,0),C(4,0),由|AB|+|AC|+|BC|=18,得|AB|+|AC|=10,因此点A的轨迹是以B,C为焦点的椭圆, 这个椭圆上的点与两焦点的距离的和2a=10,但A点不在x轴上, 由a=5,c=4,解得b2=9,因此点A的轨迹方程是 例4.如果方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围是 。解:将方程整理成 根据题意得 解得0(1)求△AF1B的周长;
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?(1) |AF1|+|AB|+|BF1|=20. (2)周长不变 课堂练习1.椭圆 上一点P到一个焦点的距离为5,则P点到另一个焦点的距离是( )
(A)5 (B)6 (C)4 (D)12A2.椭圆 的左、右焦点为F1,F2,一直线过F1交椭圆于A、B两点,则△ABF2的周长为( )
(A)32 (B)16
(C)8 (D)4B3.若△ABC的两个顶点坐标为A(-4,0),B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
(A) (B)
(C) (D)D4.已知定点F1、F2,且|F1F2|=8,动点P满足|PF1|+|PF2|=8,则动点P的轨迹是( )
(A)椭圆 (B)圆
(C)直线 (D)线段D5.椭圆5x2+ky2=5的一个焦点是(0,2),那么k的值为( )
(A)-1 (B)1
(C) (D)-B6.过点(-3,2)且与 有相同焦点的椭圆的方程为( )
(A) (B)
(C) (D)A7.已知椭圆过点P( ,-4)和点Q(- , 3),则此椭圆的标准方程是( )
(A)
(B) 或
(C)
(D)以上都不对A 8.若椭圆 的焦距是2,则m的值是( )
(A)5 (B)5或8
(C)3或5 (D)20C
|F1F2|)的点的轨迹叫椭圆.定点F1、F2叫做椭圆的焦点.2.椭圆上的点到两个焦点的距离之和为常数,记为2a;
两焦点之间的距离称为焦距,记为2c,即|F1F2|=2c.说明椭圆的定义:1.平面上这一个条件不可少;3. 2a>| F1F2|若2a=|F1F2|轨迹是什么呢?若2a<|F1F2|轨迹是什么呢?轨迹是一条线段轨迹不存在怎样推导椭圆的方程:求曲线方程的一般步骤是什么?如何建立适当的直角坐标系?原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)? 探讨建立平面直角坐标系的方案方案一(对称、“简洁”) 以过焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy,这时F1,F2的坐标分别为(-c,0),(c,0), 设M(x,y)是椭圆上的任意一点,根据椭圆的定义可知,点M在椭圆上的充分必要条件是|MF1|+|MF2|=2a,因为
所以上述条件转化为坐标表示,就是 ① 当x≠0时, 由①得 整理得 即 ② ①+②,整理得 ③ 将③式平方,再整理得 ④ 因为a>c>0,所以a2-c2>0,设a2-c2=b2>0,则④式化为 ⑤ 当x=0时,|MF1|=|MF2|=a,由 得y2=a2-c2=b2,此时M的坐标适合⑤. 因此,方程⑤是给定的椭圆的方程。
通常把这个方程叫做椭圆的标准方程。
焦点是F1(-c,0),F2(c,0),且c2=a2-b2.思考:如果椭圆的焦点在y轴上, 焦点是F1(0,-c),F2(0,c),只要将方程①的x,y互换,就可以得到它的方程,
其中b2=a2-c2,这个方程也是椭圆的标准方程。例1. 求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-3,0),(3,0),椭圆上任意一点与两焦点的距离的和等于8;解:(1)椭圆的焦点在x轴上,设它的标准方程是由已知,得2a=8,即a=4,又因为c=3,
所以b2=a2-c2=7,因此椭圆的标准方程是 解:(2)椭圆的焦点在y轴上,设它的标准方程是 由已知,得c=4,因为c2=a2-b2,
所以a2=b2+16 ①将①代入②得, 解得b2=4 (b2=-12舍去),则a2=4+16=20,因此椭圆的标准方程是 解:(1)已知方程就是椭圆的标准方程,由36>24,可知这个椭圆的焦点在x轴上,且a2=36,b2=24,所以c2=a2-b2=12, 解:(2)把已知方程化为标准方程,
由8>3可知这个椭圆的解得在y轴上,
且a2=8,b2=3,得c2=a2-b2=5,(2)8x2+3y2=24.例3. 已知B,C是两个定点,|BC|=8,且△ABC的周长等于18,求这个三角形的顶点A的轨迹方程。解:以过B,C两点的直线为x轴,线段BC的垂直平分线为y轴,建立直角坐标系xOy,
由|BC|=8,可知B(-4,0),C(4,0),由|AB|+|AC|+|BC|=18,得|AB|+|AC|=10,因此点A的轨迹是以B,C为焦点的椭圆, 这个椭圆上的点与两焦点的距离的和2a=10,但A点不在x轴上, 由a=5,c=4,解得b2=9,因此点A的轨迹方程是 例4.如果方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围是 。解:将方程整理成 根据题意得 解得0
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?(1) |AF1|+|AB|+|BF1|=20. (2)周长不变 课堂练习1.椭圆 上一点P到一个焦点的距离为5,则P点到另一个焦点的距离是( )
(A)5 (B)6 (C)4 (D)12A2.椭圆 的左、右焦点为F1,F2,一直线过F1交椭圆于A、B两点,则△ABF2的周长为( )
(A)32 (B)16
(C)8 (D)4B3.若△ABC的两个顶点坐标为A(-4,0),B(4,0),△ABC的周长为18,则顶点C的轨迹方程为( )
(A) (B)
(C) (D)D4.已知定点F1、F2,且|F1F2|=8,动点P满足|PF1|+|PF2|=8,则动点P的轨迹是( )
(A)椭圆 (B)圆
(C)直线 (D)线段D5.椭圆5x2+ky2=5的一个焦点是(0,2),那么k的值为( )
(A)-1 (B)1
(C) (D)-B6.过点(-3,2)且与 有相同焦点的椭圆的方程为( )
(A) (B)
(C) (D)A7.已知椭圆过点P( ,-4)和点Q(- , 3),则此椭圆的标准方程是( )
(A)
(B) 或
(C)
(D)以上都不对A 8.若椭圆 的焦距是2,则m的值是( )
(A)5 (B)5或8
(C)3或5 (D)20C
