2.3.2双曲线的几何性质
文档属性
| 名称 | 2.3.2双曲线的几何性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 205.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-13 00:00:00 | ||
图片预览








文档简介
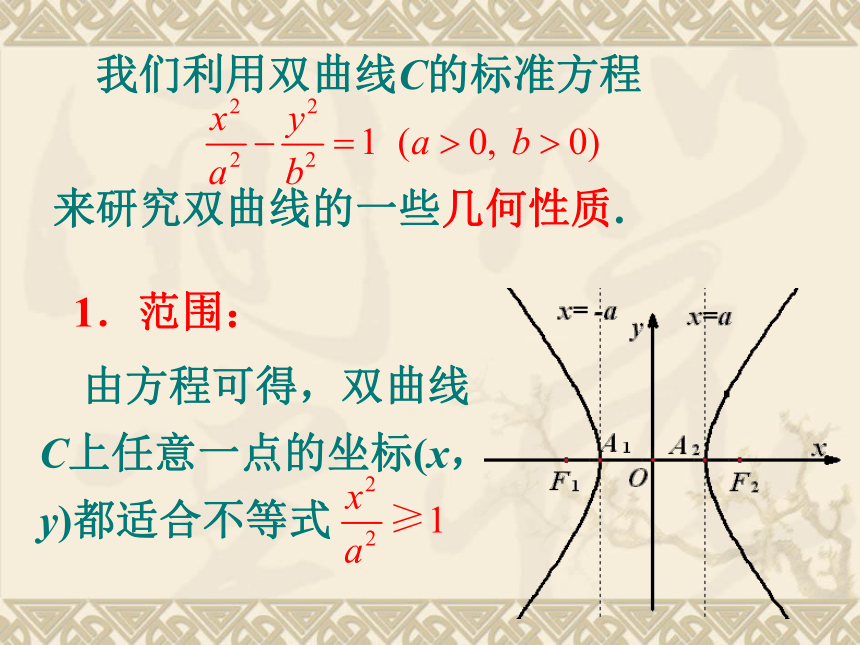
课件22张PPT。中国人民大学附属中学2.3.2双曲线的几何性质 我们利用双曲线C的标准方程
来研究双曲线的一些几何性质. 1.范围: 由方程可得,双曲线C上任意一点的坐标(x,y)都适合不等式 即x≥a,或x≤-a. 因此双曲线C位于两直线x=a和x=-a所夹平面区域的外侧。2.对称性: 类似于对椭圆对称性的讨论,可知双曲线C分别以x轴,y轴为对称轴的轴对称图形,又是以坐标原点为对称中心的中心对称图形,双曲线的对称中心又叫做双曲线的中心。3.顶点: 在方程中,令y=0,得x=±a,可知双曲线C与x轴有两个交点,分别是A1(-a,0),A2(a,0),如果令x=0,得y2=-b2,这个方程没有实数根,说明双曲线C与y轴没有公共点,
双曲线与它的对称轴的两个交点叫双曲线的顶点。 如图,双曲线C的顶点是A1(-a,0),A2(a,0),这两个顶点是双曲线两支中相距最近的点。 线段A1A2叫做双曲线的实轴,它的长等于2a,同时在y轴上作点B1(0,-b),B2(0,b),线段B1B2叫做双曲线的虚轴,它的长等于2b. 相应的a,b分别是双曲线的实半轴长和虚半轴长。 4.渐近线 观察图中方程①所表示的双曲线C,在直线x=a的右侧,当x逐渐增大时,双曲线的右支向右上和右下逐渐延伸;在直线x=-a的左侧,当x逐渐减小时,双曲线的左支向左上和左下逐渐延伸。 我们再进一步分析双曲线的这一变化趋势,不妨先考虑它在第一象限内的那一部分,这一部分的曲线的方程可以表达为 由于x>a>0,可知 又因为b>0,所以 这说明在第一象限内,双曲线C上的任意一点M(x,y)总是位于直线 的下方. 过点M作平行于y轴的直线,设它与直线
相交于点P,则因为当x>a时, 随着x的增大而增大, 可知当x越来越大时,|PM|越来越接近于0. 这说明当点M以双曲线C的顶点A2开始在第一象限沿此双曲线移动并越来越远离点A2时,点M和直线 就越来越接近。 由此可见,此双曲线右支向右上方无限延伸时,它总在直线的下方,且与直线
越来越接近,但不会相交。 根据双曲线的对称性可知,双曲线C向外无限延伸时,总是局限在由直线 和直线 相交而分平面所成的、含双曲线焦点的两个区域内,并与这两条直线无限接近,但永远不会与这两条直线相交。 直线 和直线 叫做双曲线的渐近线。5.离心率 双曲线的焦距与实轴长的比 叫做双曲线的离心率。 因为c>a>0,所以e>1,
e越趋近于1,由等式c2-a2=b2,可得 因此e越大, 也越大,即渐近线 的斜率的绝对值越大,这时双曲线的形状就从扁狭逐渐变得开阔, 双曲线的离心率越大,它的开口就越开阔。例1.已知双曲线的焦点在x轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其渐近线的方程。 解:由已知,得2c=8,2a=6,
因此c=4,a=3,b2=c2-a2=7. 又因为双曲线的焦点在x轴上,因此双曲线的标准方程是 双曲线渐近线方程是 例2.求双曲线16x2-9y2=144的实轴长和虚轴长、顶点坐标、焦点坐标及渐近线方程。解:把双曲线方程化为标准方程 由此可知,实半轴长a=3,虚半轴长b=4,半焦距c=5, 因此实轴长 2a=6;虚轴长 2b=8; 顶点坐标是(3,0),(-3,0);焦点坐标是(-5,0),(5,0); 渐近线方程是例3.一双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小直径为24m,上口直径为26m,下口直径50m,高为55m,在所给的直角坐标系中,求此双曲线的近似方程(虚半轴长精确的0.1m)。解:在给定的直角坐标系中,设双曲线的标准方程为 由已知冷却塔的最小直径AA’=24m,上口直径CC’=26m,下口直径BB’=50m,可知a=12,点B、C的横坐标分别为25,13. 设B、C的纵坐标分别为y1,y2,其中y1<0,y2>0,因为B(25,y1),C(13,y2)在双曲线上,所以因为塔高为55m,所以y2-y1=55,即因此双曲线的近似方程是 解得b≈24.5,例4.已知双曲线的渐近线方程为y=± ,并且焦点都在圆x2+y2=100上,求双曲线的方程。解:当焦点在x轴上时,设双曲线的方程是 因为焦点都在圆x2+y2=100上,所以c=10,又双曲线的渐近线方程为y=± 所以 由 解得 所以双曲线的方程是 当焦点在y轴上时,设双曲线的方程是 因为焦点都在圆x2+y2=100上,
所以c=10,又双曲线的渐近线方程为y=± 所以 解得 所以双曲线的方程是 由例5.双曲线 (a>1,b>0)的焦距为2,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥ c,求双曲线的离心率e的取值范围。解:直线l的方程为即bx+ay-ab=0, 由点到直线的距离公式,且a>1,得到点(1,0)到直线l的距离 d1= 同理点(-1,0) 到直线l的距离d2= s=d1+d2= 由s≥ c,得 即 解不等式得 ≤e2≤5, 由e>1,所以e的取值范围是
来研究双曲线的一些几何性质. 1.范围: 由方程可得,双曲线C上任意一点的坐标(x,y)都适合不等式 即x≥a,或x≤-a. 因此双曲线C位于两直线x=a和x=-a所夹平面区域的外侧。2.对称性: 类似于对椭圆对称性的讨论,可知双曲线C分别以x轴,y轴为对称轴的轴对称图形,又是以坐标原点为对称中心的中心对称图形,双曲线的对称中心又叫做双曲线的中心。3.顶点: 在方程中,令y=0,得x=±a,可知双曲线C与x轴有两个交点,分别是A1(-a,0),A2(a,0),如果令x=0,得y2=-b2,这个方程没有实数根,说明双曲线C与y轴没有公共点,
双曲线与它的对称轴的两个交点叫双曲线的顶点。 如图,双曲线C的顶点是A1(-a,0),A2(a,0),这两个顶点是双曲线两支中相距最近的点。 线段A1A2叫做双曲线的实轴,它的长等于2a,同时在y轴上作点B1(0,-b),B2(0,b),线段B1B2叫做双曲线的虚轴,它的长等于2b. 相应的a,b分别是双曲线的实半轴长和虚半轴长。 4.渐近线 观察图中方程①所表示的双曲线C,在直线x=a的右侧,当x逐渐增大时,双曲线的右支向右上和右下逐渐延伸;在直线x=-a的左侧,当x逐渐减小时,双曲线的左支向左上和左下逐渐延伸。 我们再进一步分析双曲线的这一变化趋势,不妨先考虑它在第一象限内的那一部分,这一部分的曲线的方程可以表达为 由于x>a>0,可知 又因为b>0,所以 这说明在第一象限内,双曲线C上的任意一点M(x,y)总是位于直线 的下方. 过点M作平行于y轴的直线,设它与直线
相交于点P,则因为当x>a时, 随着x的增大而增大, 可知当x越来越大时,|PM|越来越接近于0. 这说明当点M以双曲线C的顶点A2开始在第一象限沿此双曲线移动并越来越远离点A2时,点M和直线 就越来越接近。 由此可见,此双曲线右支向右上方无限延伸时,它总在直线的下方,且与直线
越来越接近,但不会相交。 根据双曲线的对称性可知,双曲线C向外无限延伸时,总是局限在由直线 和直线 相交而分平面所成的、含双曲线焦点的两个区域内,并与这两条直线无限接近,但永远不会与这两条直线相交。 直线 和直线 叫做双曲线的渐近线。5.离心率 双曲线的焦距与实轴长的比 叫做双曲线的离心率。 因为c>a>0,所以e>1,
e越趋近于1,由等式c2-a2=b2,可得 因此e越大, 也越大,即渐近线 的斜率的绝对值越大,这时双曲线的形状就从扁狭逐渐变得开阔, 双曲线的离心率越大,它的开口就越开阔。例1.已知双曲线的焦点在x轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其渐近线的方程。 解:由已知,得2c=8,2a=6,
因此c=4,a=3,b2=c2-a2=7. 又因为双曲线的焦点在x轴上,因此双曲线的标准方程是 双曲线渐近线方程是 例2.求双曲线16x2-9y2=144的实轴长和虚轴长、顶点坐标、焦点坐标及渐近线方程。解:把双曲线方程化为标准方程 由此可知,实半轴长a=3,虚半轴长b=4,半焦距c=5, 因此实轴长 2a=6;虚轴长 2b=8; 顶点坐标是(3,0),(-3,0);焦点坐标是(-5,0),(5,0); 渐近线方程是例3.一双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小直径为24m,上口直径为26m,下口直径50m,高为55m,在所给的直角坐标系中,求此双曲线的近似方程(虚半轴长精确的0.1m)。解:在给定的直角坐标系中,设双曲线的标准方程为 由已知冷却塔的最小直径AA’=24m,上口直径CC’=26m,下口直径BB’=50m,可知a=12,点B、C的横坐标分别为25,13. 设B、C的纵坐标分别为y1,y2,其中y1<0,y2>0,因为B(25,y1),C(13,y2)在双曲线上,所以因为塔高为55m,所以y2-y1=55,即因此双曲线的近似方程是 解得b≈24.5,例4.已知双曲线的渐近线方程为y=± ,并且焦点都在圆x2+y2=100上,求双曲线的方程。解:当焦点在x轴上时,设双曲线的方程是 因为焦点都在圆x2+y2=100上,所以c=10,又双曲线的渐近线方程为y=± 所以 由 解得 所以双曲线的方程是 当焦点在y轴上时,设双曲线的方程是 因为焦点都在圆x2+y2=100上,
所以c=10,又双曲线的渐近线方程为y=± 所以 解得 所以双曲线的方程是 由例5.双曲线 (a>1,b>0)的焦距为2,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥ c,求双曲线的离心率e的取值范围。解:直线l的方程为即bx+ay-ab=0, 由点到直线的距离公式,且a>1,得到点(1,0)到直线l的距离 d1= 同理点(-1,0) 到直线l的距离d2= s=d1+d2= 由s≥ c,得 即 解不等式得 ≤e2≤5, 由e>1,所以e的取值范围是
