2.4.1抛物线的标准方程
文档属性
| 名称 | 2.4.1抛物线的标准方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 162.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-13 10:59:40 | ||
图片预览








文档简介
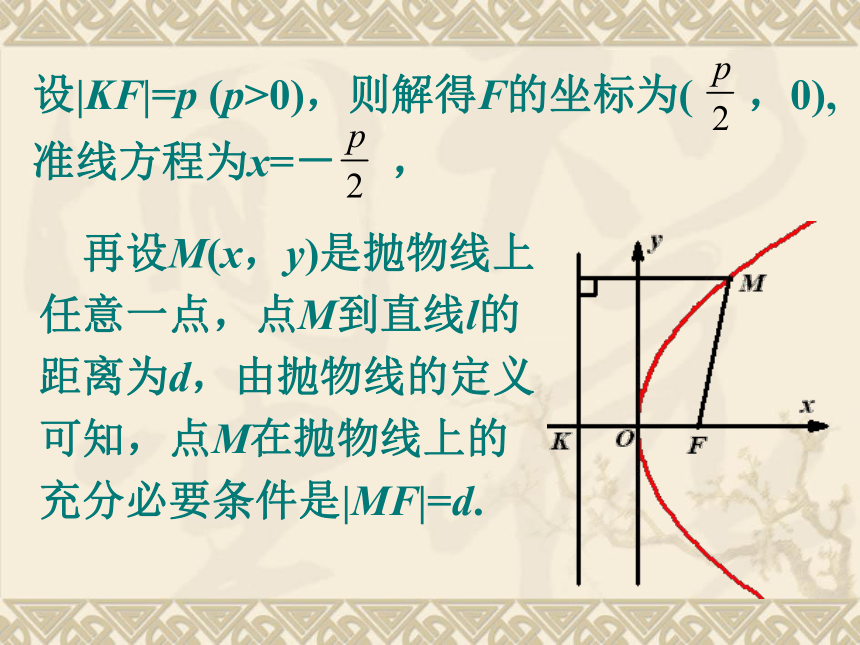
课件22张PPT。中国人民大学附属中学2.4.1抛物线的标准方程 定点F叫做抛物线的焦点,
定直线l叫做抛物线的准线。 下面我们根据抛物线的定义来探求它的方程。 过点F作直线l的垂线,垂足为K,以直线KF为x轴,线段KF的中垂线为y轴,建立直角坐标系xOy. 再设M(x,y)是抛物线上任意一点,点M到直线l的距离为d,由抛物线的定义可知,点M在抛物线上的充分必要条件是|MF|=d.所以 将上式两边平方并化简,得y2=2px (p>0). ① 方程①叫做抛物线的标准方程, 例1.已知抛物线的焦点坐标是(3,2),写出它的标准方程和准线方程。因此抛物线的标准方程是y2=12x,准线方程是x=-3.例2.已知抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,求抛物线的标准方程、焦点坐标和准线方程。解:因为抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,所以p=3, 所求的抛物线的标准方程是y2=6x, 例3.已知抛物线的顶点在原点,焦点在x轴的正半轴上,抛物线上的点M(3,m)到焦点的距离等于5,求抛物线的方程和m的值。由题意知 解得 例4.若点A的坐标为(3,2),F为抛物线y2= 2x的焦点,点P在抛物线上移动,为使得|PA|+|PF|取得最小值,则P点的坐标为 .解:由抛物线的定义,|PF|等于点P到抛物线的准线的距离|PP’|,由图可知,当且仅当P、A、P’在同一条直线上时, |PF|+|PA|=|PP’|+|PA|最小,此时点P的纵坐标等于A点的纵坐标,即P点的坐标为(2,2).课堂练习1.抛物线y2=8x的准线方程是( )
(A)x=-2 (B)x=-4
(C)y=-2 (D)y=-4A 2.顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上的抛物线方程是( )
(A)y2=4x (B)y2=8x
(C)y2=16x (D)y2=12xC3.抛物线y2=x上一点P到焦点的距离是2,则P点的坐标为( )
(A) (B)
(C) (D)B4.设抛物线y2=8px (p>0),F是它的焦点,则p表示( )
(A)F到准线的距离
(B)F到x轴的距离
(C)F到x轴距离的
(D)F到准线距离的D5.抛物线y2=4px (p>0)上一点M到焦点的距离为a,则M到y轴的距离为( )
(A)a-p (B)a+p
(C)a- (D)a+2pA6.焦点在x轴的正半轴上,并且过M(2,4)点的抛物线的标准方程是 。 y2=8x 7.已知抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,则抛物线的标准方程是 ;焦点坐标是 ;准线方程是 。y2=6x 8.已知P是抛物线y2=16x上一点,它到x轴的距离为12,则它到焦点的距离是 。139.以双曲线 的右焦点为焦点,且以原点为顶点的抛物线的标准方程是 。 y2=20x 10.斜率是1的直线经过抛物线y2=4x的焦点,与抛物线相交于A、B两点,则线段AB的长等于 .8 11.方程mx+ny2=0与mx2+ny2=1(mn≠0)在同一坐标系中的图象大致是( )。 (A) (B) (C) (D)A 12.抛物线y2=2x上两点A, B到焦点的距离之和是5,则线段AB中点的横坐标是 .2 13.抛物线型拱桥,当水面离拱顶2m时,水面宽4m,若水面下降1m后,则水面宽是 . 14.有一个正三角形,它的两个顶点在抛物线y2=-4x上,另一个顶点在原点,则此正三角形的面积是 .
定直线l叫做抛物线的准线。 下面我们根据抛物线的定义来探求它的方程。 过点F作直线l的垂线,垂足为K,以直线KF为x轴,线段KF的中垂线为y轴,建立直角坐标系xOy. 再设M(x,y)是抛物线上任意一点,点M到直线l的距离为d,由抛物线的定义可知,点M在抛物线上的充分必要条件是|MF|=d.所以 将上式两边平方并化简,得y2=2px (p>0). ① 方程①叫做抛物线的标准方程, 例1.已知抛物线的焦点坐标是(3,2),写出它的标准方程和准线方程。因此抛物线的标准方程是y2=12x,准线方程是x=-3.例2.已知抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,求抛物线的标准方程、焦点坐标和准线方程。解:因为抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,所以p=3, 所求的抛物线的标准方程是y2=6x, 例3.已知抛物线的顶点在原点,焦点在x轴的正半轴上,抛物线上的点M(3,m)到焦点的距离等于5,求抛物线的方程和m的值。由题意知 解得 例4.若点A的坐标为(3,2),F为抛物线y2= 2x的焦点,点P在抛物线上移动,为使得|PA|+|PF|取得最小值,则P点的坐标为 .解:由抛物线的定义,|PF|等于点P到抛物线的准线的距离|PP’|,由图可知,当且仅当P、A、P’在同一条直线上时, |PF|+|PA|=|PP’|+|PA|最小,此时点P的纵坐标等于A点的纵坐标,即P点的坐标为(2,2).课堂练习1.抛物线y2=8x的准线方程是( )
(A)x=-2 (B)x=-4
(C)y=-2 (D)y=-4A 2.顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上的抛物线方程是( )
(A)y2=4x (B)y2=8x
(C)y2=16x (D)y2=12xC3.抛物线y2=x上一点P到焦点的距离是2,则P点的坐标为( )
(A) (B)
(C) (D)B4.设抛物线y2=8px (p>0),F是它的焦点,则p表示( )
(A)F到准线的距离
(B)F到x轴的距离
(C)F到x轴距离的
(D)F到准线距离的D5.抛物线y2=4px (p>0)上一点M到焦点的距离为a,则M到y轴的距离为( )
(A)a-p (B)a+p
(C)a- (D)a+2pA6.焦点在x轴的正半轴上,并且过M(2,4)点的抛物线的标准方程是 。 y2=8x 7.已知抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,则抛物线的标准方程是 ;焦点坐标是 ;准线方程是 。y2=6x 8.已知P是抛物线y2=16x上一点,它到x轴的距离为12,则它到焦点的距离是 。139.以双曲线 的右焦点为焦点,且以原点为顶点的抛物线的标准方程是 。 y2=20x 10.斜率是1的直线经过抛物线y2=4x的焦点,与抛物线相交于A、B两点,则线段AB的长等于 .8 11.方程mx+ny2=0与mx2+ny2=1(mn≠0)在同一坐标系中的图象大致是( )。 (A) (B) (C) (D)A 12.抛物线y2=2x上两点A, B到焦点的距离之和是5,则线段AB中点的横坐标是 .2 13.抛物线型拱桥,当水面离拱顶2m时,水面宽4m,若水面下降1m后,则水面宽是 . 14.有一个正三角形,它的两个顶点在抛物线y2=-4x上,另一个顶点在原点,则此正三角形的面积是 .
