1.3正方形的判定 教学设计 北师大版数学九年级上册
文档属性
| 名称 | 1.3正方形的判定 教学设计 北师大版数学九年级上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 995.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 20:39:04 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 正方形的性质与判定(第二课时)
教科书 书 名:数学教材出版社:北京师范大学出版社
教学目标
1.经历“探索—发现—猜想—证明”的过程,掌握正方形的判定定理,发现决定中点四边形形状的因素,并能综合运用特殊四边形的性质和判定解决问题,进一步发展逻辑推理能力。2.通过凸四边形的中点四边形的探求过程,引导学生体会证明过程中所运用的由一般到特殊再到一般的归纳、类比、转化的思想方法等,培养积极探索、勇于创新的精神,以及推陈出新的创新能力。3.通过师生互动、生生合作交流以及多媒体课件的使用,进一步发展学生合作交流的能力和数学表达能力,并使学生发现数学中蕴涵的美,激发学生学习的自觉性、积极性,提高学习数学的兴趣。
教学内容
教学重点:1. 掌握正方形的判定定理,发现决定中点四边形形状的因素。
教学难点:1. 综合运用特殊四边形的性质和判定解决问题。
教学过程
教学环节 教师活动 学生活动 设计意图
一、类比经验,提出目标 引导学生类比《菱形的判定》和《矩形的判定》这两节课的学习过程,获得本节课的学习目标。 类比已有经验,获得学习目标。 学习最终是走上自学的道路,学生必须自己形成知识建构。
二、知识回顾,导入新课 回顾前面所学知识,如何得到菱形和矩形? 将自己做的四边形纸片展示在黑板上,并归纳菱形和矩形的判定方法。 以形入手,直观想象。对本章前面所学知识形成清晰的脉络。
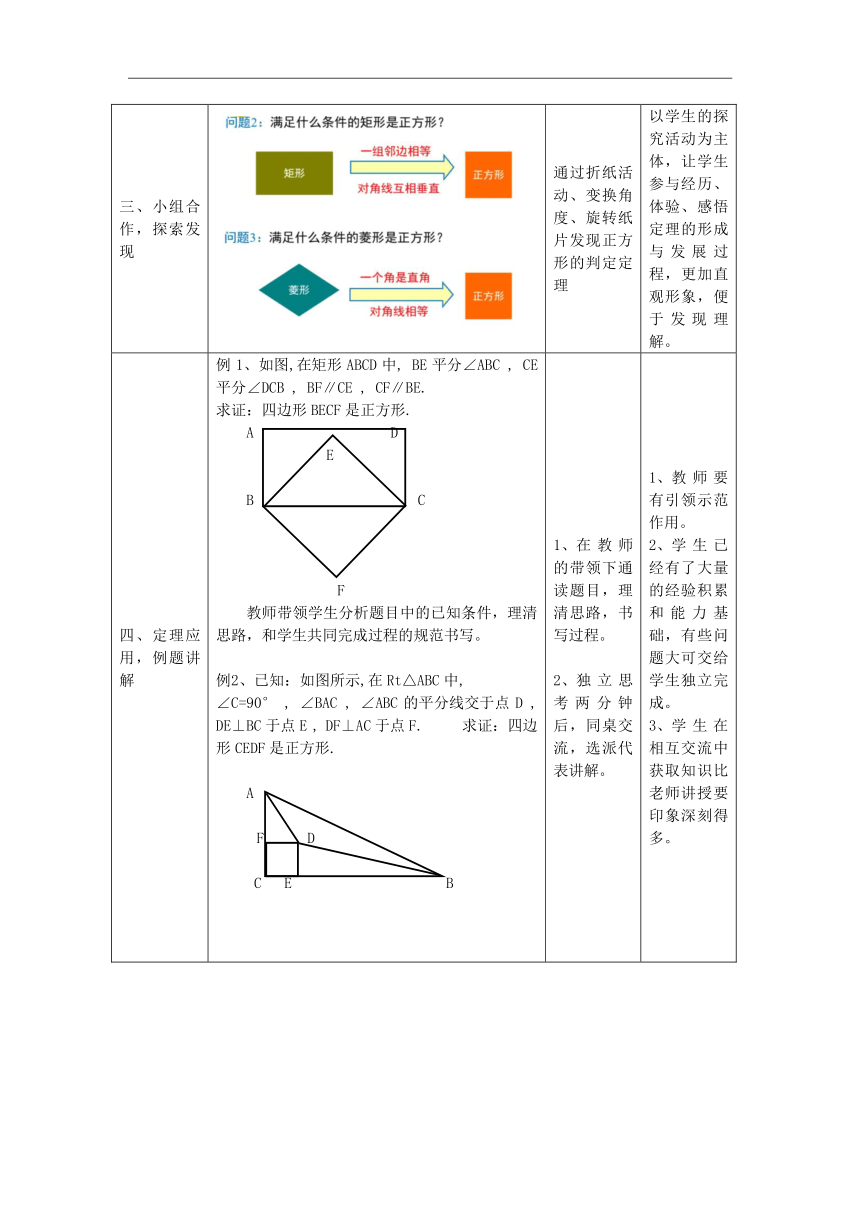
三、小组合作,探索发现 通过折纸活动、变换角度、旋转纸片发现正方形的判定定理 以学生的探究活动为主体,让学生参与经历、体验、感悟定理的形成与发展过程,更加直观形象,便于发现理解。
四、定理应用,例题讲解 例1、如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.求证:四边形BECF是正方形. A D E B C F教师带领学生分析题目中的已知条件,理清思路,和学生共同完成过程的规范书写。已知:如图所示,在Rt△ABC中, ∠C=90° , ∠BAC , ∠ABC的平分线交于点D , DE⊥BC于点E , DF⊥AC于点F. 求证:四边形CEDF是正方形. AF D C E B 在教师的带领下通读题目,理清思路,书写过程。独立思考两分钟后,同桌交流,选派代表讲解。 教师要有引领示范作用。学生已经有了大量的经验积累和能力基础,有些问题大可交给学生独立完成。学生在相互交流中获取知识比老师讲授要印象深刻得多。
五、小组合作,再探新知 依次连接下面各四边形各边中点,得到什么图形?中点四边形的形状和原四边形的对角线有什么关系?原四边形对角线的特点举例任意四边形矩形菱形正方形中点四边形形状教师带领学生从特殊入手,便于发现规律,再抽象到一般情形,使所学知识得到升华。 1、动手画图,小组交流,获得结果。2、合情推理,抽象概括,获得更具一般性的结论。 数学是一门严密的学科,是透过现象窥探本质的一门学科。学生畅所欲言,在“以生为本”的民主氛围中培养学生抽象概括能力和语言表达能力以及严密的数学推理能力
六、知识运用,巩固提升 1.顺次连接对角线互相垂直的四边形中点,所得图形一定是( ) A.直角梯形 B.菱形 C.矩形 D.平行四边形 1、让学生用已获得的知识去解决新问题,这样做可以培养学生“学以致用”的思想。
六、知识运用,巩固提升 2.如图,在四边形ABCD中, AB=BC ,对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD ,垂足分别为M、N. (1) 求证:∠ADB=∠CDB; (2) 若∠ADC=900,求证:四边形MPND是正方形. 知识应用,巩固提升 2、让学生感受到数学学习的逻辑严密性。3、变式训练,巩固提高,使学生知识技能螺旋式的上升,及时反馈。
七、反思小结,提炼规律 鼓励学生大胆积极发言,各抒己见 使学生头脑中存储着一个层次分明的知识系统。
八、布置作业,提高升华 1、基础作业:整理正方形的判定知识框图2、提高作业:完成《绩优学案》对应练习3、创新作业:完成本章知识思维导图 鼓励学生在完成基础训练的基础上,向更高更远发展 在完成达标的基础上拓宽和加深,加强学生综合能力和创造才能的培养。也是尊重学生个体差异的表现。
板书设计 1.3.2正方形的判定一、正方形的判定判定的应用 学生板演区原四边形对角线的特点举例任意四边形矩形菱形正方形中点四边形形状三、中点四边形 通过课件展示, 清晰明了,但是必要的板书必不可少,因为这样更容易让学生了解知识的生成过程,让学生对所学知识加深理解板书的同时给学生留下展示的空间,整个课堂始终不忘以学生为主体。
C
A
B
D
P
M
N
PAGE
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 正方形的性质与判定(第二课时)
教科书 书 名:数学教材出版社:北京师范大学出版社
教学目标
1.经历“探索—发现—猜想—证明”的过程,掌握正方形的判定定理,发现决定中点四边形形状的因素,并能综合运用特殊四边形的性质和判定解决问题,进一步发展逻辑推理能力。2.通过凸四边形的中点四边形的探求过程,引导学生体会证明过程中所运用的由一般到特殊再到一般的归纳、类比、转化的思想方法等,培养积极探索、勇于创新的精神,以及推陈出新的创新能力。3.通过师生互动、生生合作交流以及多媒体课件的使用,进一步发展学生合作交流的能力和数学表达能力,并使学生发现数学中蕴涵的美,激发学生学习的自觉性、积极性,提高学习数学的兴趣。
教学内容
教学重点:1. 掌握正方形的判定定理,发现决定中点四边形形状的因素。
教学难点:1. 综合运用特殊四边形的性质和判定解决问题。
教学过程
教学环节 教师活动 学生活动 设计意图
一、类比经验,提出目标 引导学生类比《菱形的判定》和《矩形的判定》这两节课的学习过程,获得本节课的学习目标。 类比已有经验,获得学习目标。 学习最终是走上自学的道路,学生必须自己形成知识建构。
二、知识回顾,导入新课 回顾前面所学知识,如何得到菱形和矩形? 将自己做的四边形纸片展示在黑板上,并归纳菱形和矩形的判定方法。 以形入手,直观想象。对本章前面所学知识形成清晰的脉络。
三、小组合作,探索发现 通过折纸活动、变换角度、旋转纸片发现正方形的判定定理 以学生的探究活动为主体,让学生参与经历、体验、感悟定理的形成与发展过程,更加直观形象,便于发现理解。
四、定理应用,例题讲解 例1、如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.求证:四边形BECF是正方形. A D E B C F教师带领学生分析题目中的已知条件,理清思路,和学生共同完成过程的规范书写。已知:如图所示,在Rt△ABC中, ∠C=90° , ∠BAC , ∠ABC的平分线交于点D , DE⊥BC于点E , DF⊥AC于点F. 求证:四边形CEDF是正方形. AF D C E B 在教师的带领下通读题目,理清思路,书写过程。独立思考两分钟后,同桌交流,选派代表讲解。 教师要有引领示范作用。学生已经有了大量的经验积累和能力基础,有些问题大可交给学生独立完成。学生在相互交流中获取知识比老师讲授要印象深刻得多。
五、小组合作,再探新知 依次连接下面各四边形各边中点,得到什么图形?中点四边形的形状和原四边形的对角线有什么关系?原四边形对角线的特点举例任意四边形矩形菱形正方形中点四边形形状教师带领学生从特殊入手,便于发现规律,再抽象到一般情形,使所学知识得到升华。 1、动手画图,小组交流,获得结果。2、合情推理,抽象概括,获得更具一般性的结论。 数学是一门严密的学科,是透过现象窥探本质的一门学科。学生畅所欲言,在“以生为本”的民主氛围中培养学生抽象概括能力和语言表达能力以及严密的数学推理能力
六、知识运用,巩固提升 1.顺次连接对角线互相垂直的四边形中点,所得图形一定是( ) A.直角梯形 B.菱形 C.矩形 D.平行四边形 1、让学生用已获得的知识去解决新问题,这样做可以培养学生“学以致用”的思想。
六、知识运用,巩固提升 2.如图,在四边形ABCD中, AB=BC ,对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD ,垂足分别为M、N. (1) 求证:∠ADB=∠CDB; (2) 若∠ADC=900,求证:四边形MPND是正方形. 知识应用,巩固提升 2、让学生感受到数学学习的逻辑严密性。3、变式训练,巩固提高,使学生知识技能螺旋式的上升,及时反馈。
七、反思小结,提炼规律 鼓励学生大胆积极发言,各抒己见 使学生头脑中存储着一个层次分明的知识系统。
八、布置作业,提高升华 1、基础作业:整理正方形的判定知识框图2、提高作业:完成《绩优学案》对应练习3、创新作业:完成本章知识思维导图 鼓励学生在完成基础训练的基础上,向更高更远发展 在完成达标的基础上拓宽和加深,加强学生综合能力和创造才能的培养。也是尊重学生个体差异的表现。
板书设计 1.3.2正方形的判定一、正方形的判定判定的应用 学生板演区原四边形对角线的特点举例任意四边形矩形菱形正方形中点四边形形状三、中点四边形 通过课件展示, 清晰明了,但是必要的板书必不可少,因为这样更容易让学生了解知识的生成过程,让学生对所学知识加深理解板书的同时给学生留下展示的空间,整个课堂始终不忘以学生为主体。
C
A
B
D
P
M
N
PAGE
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
