2025高考物理二轮复习专题四-电路和电磁感应-第8讲 电磁感应中的双杆和线框模型 课件 (共45张PPT)
文档属性
| 名称 | 2025高考物理二轮复习专题四-电路和电磁感应-第8讲 电磁感应中的双杆和线框模型 课件 (共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览








文档简介
(共45张PPT)
第8讲 电磁感应中的双杆和线框模型
角度1 双杆模型
角度2 线框模型
跟踪训练
备用习题
基本模型 图例 运动特点 图像 最终特征
无外力等 距式 ____________________________________ 棒1做加速度减 小的加速运动, 棒2做加速度减 小的减速运动 _________________________________________ ,
系统动量守恒
基本模型 图例 运动特点 图像 最终特征
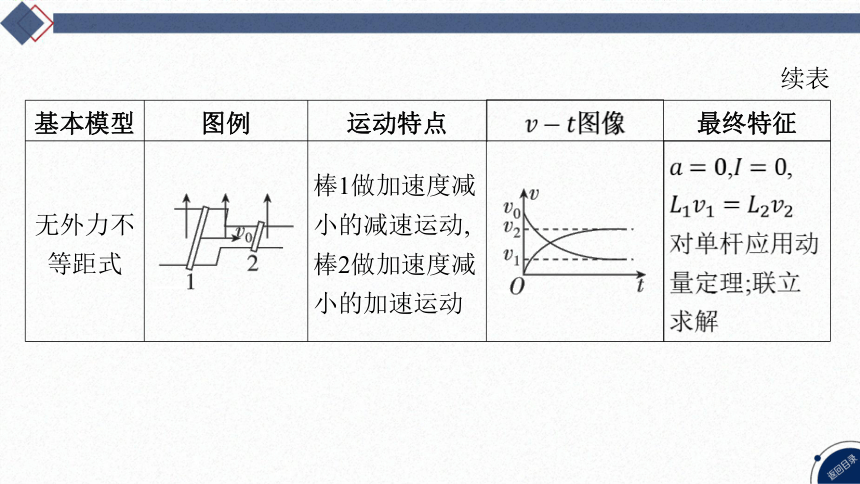
无外力不 等距式 _____________________________________ 棒1做加速度减 小的减速运动, 棒2做加速度减 小的加速运动 _______________________________________ , ,
对单杆应用动
量定理;联立
求解
续表
基本模型 图例 运动特点 图像 最终特征
有外力等 距式 ____________________________________ 棒1做加速度增 大的加速运动, 棒2做加速度减 小的加速运动 ______________________________________ ,、
恒定
对单杆应用动
量定理,稳定
后对单杆应用
牛顿第二定
律;联立求解
续表
角度1 双杆模型
例1 如图所示,在空间中有上、下两个足够长的水平光滑平行金属导轨
、和水平光滑平行金属导轨、 ,平行导轨间距均为
,导轨电阻不计,上、下两导轨的高度差为 ,上导轨
最左端接一电阻 .虚线左侧宽度的 区域内
存在着竖直向下的匀强磁场,磁感应强度随时间变化规律为
;虚线右侧 区域内存在竖直向上的匀强磁场,
磁感应强度;竖直线与 的右侧空间存在竖直向上的匀强
磁场,磁感应强度 .上、下导轨中垂直于导轨分别放置相同的导
体棒和导体棒,棒长均为,质量均为 ,电阻均为
.时刻闭合开关,导体棒 在安培力的作用下开始运动,
导体棒在离开上导轨、前已经达到稳定状态.导体棒从 离
开下落到下导轨上时,竖直速度立即变为零,水平速度不变.重力加速度
取 .
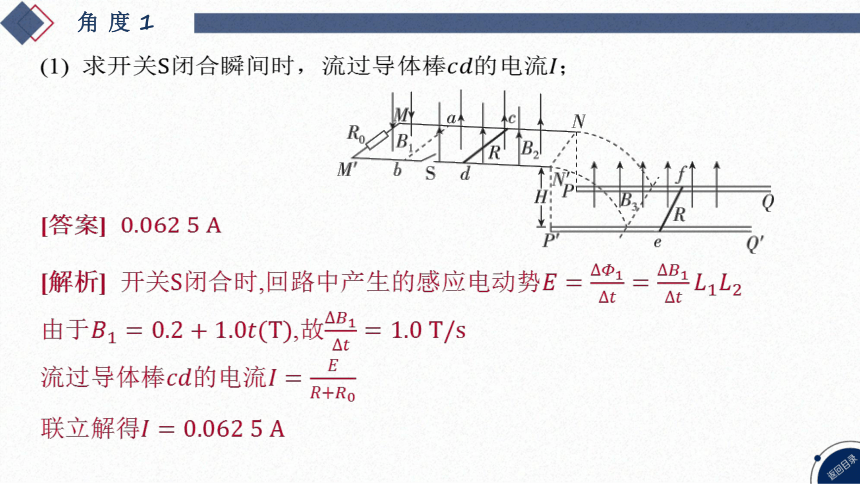
(1) 求开关闭合瞬间时,流过导体棒的电流 ;
[答案]
[解析] 开关闭合时,回路中产生的感应电动势
由于,故
流过导体棒的电流
联立解得
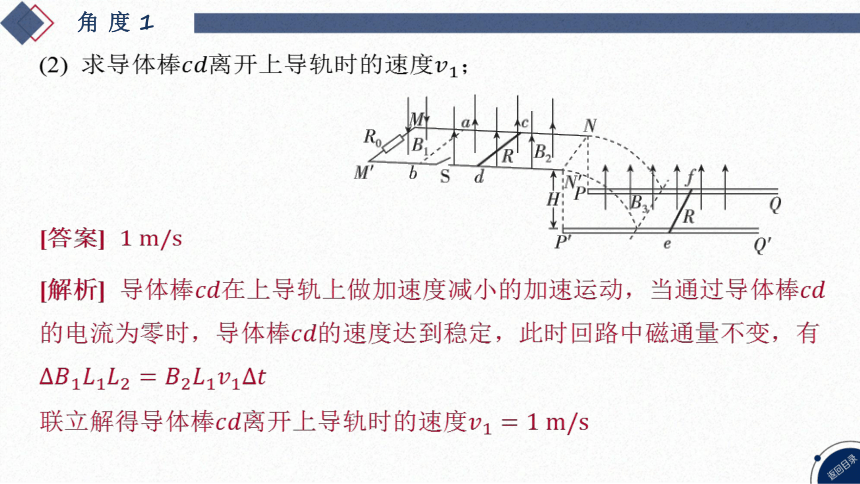
(2) 求导体棒离开上导轨时的速度 ;
[答案]
[解析] 导体棒在上导轨上做加速度减小的加速运动,当通过导体棒
的电流为零时,导体棒 的速度达到稳定,此时回路中磁通量不变,有
联立解得导体棒离开上导轨时的速度
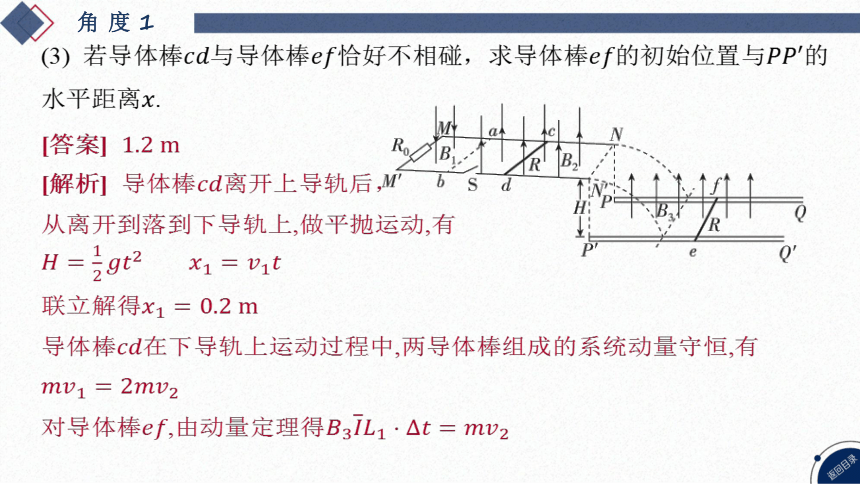
(3) 若导体棒与导体棒恰好不相碰,求导体棒的初始位置与 的
水平距离 .
[答案]
[解析] 导体棒 离开上导轨后,
从离开到落到下导轨上,做平抛运动,有
联立解得
导体棒 在下导轨上运动过程中,两导体棒组成的系统动量守恒,有
对导体棒,由动量定理得
其中,,
联立解得
由于导体棒与导体棒恰好不相碰,故导体棒的初始位置与 的水
平距离
角度2 线框模型
例2 [2024·温州模拟] 电动汽车可以利用电磁相关原理进行驱动和制动并
进行动能回收,其中一种轮毂电机可以通过控制定子绕组通电顺序和时间,
形成旋转磁场,驱动转子绕组带动轮胎转动,其展开简化模型如图甲所示.
定子产生一个个边长为的正方形匀强磁场,磁感应强度大小均为 ,相邻
磁场方向相反.转子绕组可简化为一个水平放置的正方形线圈,质量为 ,
匝数为,边长为,总电阻为,线圈运动时受到恒定阻力 .不考虑定子
发热损耗和磁场运动引起的电磁辐射.
[解析] 线圈达到最大速度时,产生的感应电动势
线圈中的电流
线圈受到的安培力
此时线圈也匀速运动,受力平衡,有
联立解得
(1) 若磁场以速度向右匀速运动,求线圈能达到的最大速度 ;
[答案]
(2) 若磁场从 时刻开始由静止匀加速运动,经过一段时间,线圈也匀
加速运动,时刻速度为,求线圈的加速度大小 ;
[答案]
[解析] 对线圈,根据牛顿第二定律有
其中,,
联立可得
由于线圈也做匀加速运动,即不变,则 应不变,说明磁场的
加速度也为, 时刻有
解得
(3) 制动时,磁场立刻停下,此时速度为 的线圈通过整流装置可以给电
动势为的动力电池充电,此过程线圈的 图像如图乙所示,
则此制动过程给动力电池充入的电荷量约为多少?
[答案]
[解析] 制动时,线圈给电池充电,有
当时,线圈不再给电池充电,由于 ,故此时线圈速度
由图像可知对应 时刻.在这段时间内,有
其中,在图像中,对应速度由到 段图线围成的面积,利
用数格法计算,
由于
联立解得
1. 如图所示,足够长的光滑平行金属导轨MN、PQ,间距为L,导轨电阻不计;左端向上弯曲,水平段导轨所处空间有两个有界匀强磁场(相距一段距离,不重叠),磁场Ⅰ区的磁感应强度为B,方向竖直向上,左边界在水平段导轨的最左端;磁场Ⅱ区的磁感应强度为2B,方向竖直向下.质量均为m、电阻均为R的金属棒a、b垂直放置在导轨上(b在区域Ⅱ内),现将金属棒a从弯曲导轨上距水平段导轨高h处由静止释放,金属棒a、b始终垂直导轨且接触良好,重力加速度为g.则:
(1)求金属棒a刚进入磁场Ⅰ区时,金属棒b的加速度;
[答案],方向向左
[解析] a棒下滑过程中由机械能守恒
定律得mgh=m解得v0=
a棒刚进入磁场Ⅰ区时,有E=BLv0
此时通过a、b棒的感应电流I=
对b棒,F安=2BIL=
则a=,方向向左.
(2)设两磁场区足够大(即a、b分别在磁场Ⅰ、Ⅱ运动),回路中最多能产生的焦耳热有多少
[答案]
[解析] 当金属棒a进入磁场 Ⅰ 后 , a棒向右减速,b棒向左加速,最终达到稳定状态,
有BLv1=2BLv2,得v1=2v2
设向右为正方向,对金属棒a,由动量定理有-BLi·t=mv1-mv0
对金属棒b,由动量定理有-2BLi·t=-mv2-0 ,解得v1= ,v2=
根据能量守恒定律知,回路中产生的最多的焦耳热
Q=mgh-
2. 如图所示,在水平面内固定一足够长的光滑平行金属导轨ab-a'b'与cdef-c'd'e'f',b与c之间以及b'与c'之间分别通过一小段长度可忽略的绝缘光滑轨道平滑连接,其中abcd-a'b'c'd'部分的宽度为2d,ef-e'f'部分的宽度为d,导轨最左端a、a'之间连接有一带电的、电容为C的电容器和开关S,整个导轨所在空间存在方向竖直向上、磁感应强度大小为B的匀强磁场.开始时开关断开,质量为m,长度为d,阻值为R的金属棒N静止在导轨ef-e'f'部分上,质量为2m,长度为2d,电阻可忽略不计的金属棒M静止在导轨ab-a'b'部分上.现闭合开关S,电容器C通过金属棒M放电,金属棒M开始沿导轨向右运动,且离开ab-a'b'部分前的一段距离内金属棒M以速度大小v0匀速运动.不计导轨电阻,两金属棒运动过程中始终与导轨垂直且接触良好,金属棒M始终在abcd-a'b'c'd'部分运动,求:
(1)金属棒M刚滑上导轨cdef-c'd'e'f'部分时加速度的大小;
[答案]
[解析] 金属棒M刚滑上导轨cdef-c'd'e'f'部分时,回路中的电流大小为I1=
E=2Bdv0
由牛顿第二定律可知金属棒M的加速度大小为a=
解得a=
(2)电容器初始时的带电荷量;
[答案] +2Bdv0C
[解析] 闭合开关S,设金属棒M速度达到稳定前某时刻的电流为I,金属棒M受到的安培力大小为F=BI·2d
在一小段时间Δt内,由动量定理可得F·Δt=2m·Δv
通过金属棒M的电荷量为Δq=I·Δt
从闭合开关S到金属棒M速度达到稳定的过程中累加求和有Bq·2d=2mv0-0
金属棒M速度稳定时切割磁感线产生的电动势为 E'=B·2dv0
此时电容器剩余的电荷量为Q1=CE'
所以电容器初始时的带电荷量为Q=q+Q1=+2Bdv0C
(3)整个过程中金属棒N产生的焦耳热.
[答案] m
[解析] 金属棒M滑上导轨cdef-c'd'e'f'部分后,流过金属棒M和金属棒N的电流大小相等,当回路中的电流为0时,两金属棒速度达到稳定,此时有B·2dv1=Bdv2
从金属棒M滑上导轨cdef-c'd'e'f'部分到速度达到稳定的过程中,根据动量定理可知,对金属棒M有Bq'·2d=2mv0-2mv1
对金属棒N有Bq'd=mv2-0
由能量守恒定律可得·2m·2mm+Q热
解得Q热=m
1.如图甲所示,在光滑的水平面上有一质量、足够长的 形金属
导轨,导轨间距.一阻值 的细导体棒 垂直于导轨
放置,并被固定在水平面上的两立柱挡住,导体棒 与导轨间的动摩擦
因数,在、两端接有一理想电压表(图中未画出).在形导轨
边初始位置右侧存在垂直于导轨平面向下、磁感应强度大小 的匀
强磁场,在两立柱左侧 形导轨内存在方向水平向左、磁感应强度大小为
的匀强磁场.以形导轨的点初始位置为原点,以沿 方向为正方向,
建立坐标轴时,形导轨的边在沿轴正方向的外力 作用下从
静止开始运动,电压表测得电压与时间的关系如图乙所示.经过 时间,
撤去外力,直至形导轨静止.已知内外力做功 .不计其他
电阻,导体棒始终与导轨垂直,忽略导体棒 的重力.
(1) 求在内外力随时间 的变化规律;
[答案]
[解析] 根据法拉第电磁感应定律可知
由于只有导体棒有电阻,故、两端电压等于产生的感应电动势 .
由图像可知
联立得
根据速度与时间关系可知
由于忽略导体棒的重力,所以摩擦力
对形金属导轨,根据牛顿第二定律有
其中
联立解得
[解析] 由功能关系得
由于摩擦力与安培力的关系为,故
则
解得
(2) 求在整个运动过程中电路产生的焦耳热 ;
[答案]
(3) 写出在整个运动过程中形导轨的边的速度与位置 的函数关系式.
[答案] 见解析
[解析] 撤去外力的时刻为时,形导轨的边在 时间内
做匀加速直线运动,在 后做非匀变速直线运动.
①时,根据位移与速度关系可知
根据匀变速直线运动规律可知,时形导轨的 边的速度为
位移为
②时,形导轨的 边做非匀变速直线运动直到停止,由动量定
理得
其中
联立解得
当时,
综上所述,边的速度与位置 的函数关系式如下:
2.[2024·杭州模拟] 如图所示,固定
的一对长金属导轨间距为 ,
其水平部分与倾斜部分均足够长.导
轨的水平部分处于竖直向上的匀强磁
场中,磁感应强度大小为 ,其左侧
连接了电源 .导轨的倾斜部分倾角
且处于平行于斜面向上的匀
强磁场中,磁感应强度大小为 ,其
下方接有开关和电容 的电
容器,开始时开关断开、电容器不带
电.导轨上正对的、 两处各有一小
段用绝缘材料制成,长度不计.质量
均为 的导电杆甲、乙静
止在导轨上,均与导轨垂直,甲与导
轨间的摩擦不计,甲的电阻
, 乙的电阻 .某时
刻起电源 开始工作,输出恒定电流
,经 ,使甲运动到
、处,电源 立即停止工作.当甲
越过、 瞬间,再对其施加一个沿
导轨水平向右的恒力 ,此时
乙恰好开始运动. 已知 ,
不计除导电杆外所有电阻,不计回路
自身激发磁场,最大静摩擦力等于滑
动摩擦力, ,
.
(1) 求甲通过、 时的速度大小;
[答案]
[解析] 对甲导电杆进行分析,根据牛
顿第二定律有
根据运动学公式有
联立解得
(2) 求乙与倾斜导轨间的动摩擦因数;
[答案]
[解析] 甲导电杆刚刚通过、 时产生的
感应电动势
感应电流
根据右手定则可知,回路中电流方向为逆
时针,根据左手定则可知,乙导电杆所
受安培力方向垂直于斜面向上,大小为
此时乙导电杆恰好开始运动,有
联立解得
(3) 求电源 输出的总能量;
[答案]
[解析] 根据能量守恒定律可知,电源
输出的总能量
联立解得
(4) 为回收部分能量,闭合开关,其他条件不变,已知在甲通过、 后
内位移为,产生的焦耳热为 ,此时电容器已达到最大稳定电
压.当电容器电压为时,其储能为 .忽略电磁辐射,求此过程
中乙上产生的焦耳热.
[答案]
[解析] 甲导电杆越过、 后,在拉力作
用下,甲导电杆向右先做加速度减小的
加速运动,最后做匀速直线运动,匀速
运动时受力平衡,有
感应电流
对甲导电杆,根据动能定理有
根据功能关系有
其中
联立解得
第8讲 电磁感应中的双杆和线框模型
角度1 双杆模型
角度2 线框模型
跟踪训练
备用习题
基本模型 图例 运动特点 图像 最终特征
无外力等 距式 ____________________________________ 棒1做加速度减 小的加速运动, 棒2做加速度减 小的减速运动 _________________________________________ ,
系统动量守恒
基本模型 图例 运动特点 图像 最终特征
无外力不 等距式 _____________________________________ 棒1做加速度减 小的减速运动, 棒2做加速度减 小的加速运动 _______________________________________ , ,
对单杆应用动
量定理;联立
求解
续表
基本模型 图例 运动特点 图像 最终特征
有外力等 距式 ____________________________________ 棒1做加速度增 大的加速运动, 棒2做加速度减 小的加速运动 ______________________________________ ,、
恒定
对单杆应用动
量定理,稳定
后对单杆应用
牛顿第二定
律;联立求解
续表
角度1 双杆模型
例1 如图所示,在空间中有上、下两个足够长的水平光滑平行金属导轨
、和水平光滑平行金属导轨、 ,平行导轨间距均为
,导轨电阻不计,上、下两导轨的高度差为 ,上导轨
最左端接一电阻 .虚线左侧宽度的 区域内
存在着竖直向下的匀强磁场,磁感应强度随时间变化规律为
;虚线右侧 区域内存在竖直向上的匀强磁场,
磁感应强度;竖直线与 的右侧空间存在竖直向上的匀强
磁场,磁感应强度 .上、下导轨中垂直于导轨分别放置相同的导
体棒和导体棒,棒长均为,质量均为 ,电阻均为
.时刻闭合开关,导体棒 在安培力的作用下开始运动,
导体棒在离开上导轨、前已经达到稳定状态.导体棒从 离
开下落到下导轨上时,竖直速度立即变为零,水平速度不变.重力加速度
取 .
(1) 求开关闭合瞬间时,流过导体棒的电流 ;
[答案]
[解析] 开关闭合时,回路中产生的感应电动势
由于,故
流过导体棒的电流
联立解得
(2) 求导体棒离开上导轨时的速度 ;
[答案]
[解析] 导体棒在上导轨上做加速度减小的加速运动,当通过导体棒
的电流为零时,导体棒 的速度达到稳定,此时回路中磁通量不变,有
联立解得导体棒离开上导轨时的速度
(3) 若导体棒与导体棒恰好不相碰,求导体棒的初始位置与 的
水平距离 .
[答案]
[解析] 导体棒 离开上导轨后,
从离开到落到下导轨上,做平抛运动,有
联立解得
导体棒 在下导轨上运动过程中,两导体棒组成的系统动量守恒,有
对导体棒,由动量定理得
其中,,
联立解得
由于导体棒与导体棒恰好不相碰,故导体棒的初始位置与 的水
平距离
角度2 线框模型
例2 [2024·温州模拟] 电动汽车可以利用电磁相关原理进行驱动和制动并
进行动能回收,其中一种轮毂电机可以通过控制定子绕组通电顺序和时间,
形成旋转磁场,驱动转子绕组带动轮胎转动,其展开简化模型如图甲所示.
定子产生一个个边长为的正方形匀强磁场,磁感应强度大小均为 ,相邻
磁场方向相反.转子绕组可简化为一个水平放置的正方形线圈,质量为 ,
匝数为,边长为,总电阻为,线圈运动时受到恒定阻力 .不考虑定子
发热损耗和磁场运动引起的电磁辐射.
[解析] 线圈达到最大速度时,产生的感应电动势
线圈中的电流
线圈受到的安培力
此时线圈也匀速运动,受力平衡,有
联立解得
(1) 若磁场以速度向右匀速运动,求线圈能达到的最大速度 ;
[答案]
(2) 若磁场从 时刻开始由静止匀加速运动,经过一段时间,线圈也匀
加速运动,时刻速度为,求线圈的加速度大小 ;
[答案]
[解析] 对线圈,根据牛顿第二定律有
其中,,
联立可得
由于线圈也做匀加速运动,即不变,则 应不变,说明磁场的
加速度也为, 时刻有
解得
(3) 制动时,磁场立刻停下,此时速度为 的线圈通过整流装置可以给电
动势为的动力电池充电,此过程线圈的 图像如图乙所示,
则此制动过程给动力电池充入的电荷量约为多少?
[答案]
[解析] 制动时,线圈给电池充电,有
当时,线圈不再给电池充电,由于 ,故此时线圈速度
由图像可知对应 时刻.在这段时间内,有
其中,在图像中,对应速度由到 段图线围成的面积,利
用数格法计算,
由于
联立解得
1. 如图所示,足够长的光滑平行金属导轨MN、PQ,间距为L,导轨电阻不计;左端向上弯曲,水平段导轨所处空间有两个有界匀强磁场(相距一段距离,不重叠),磁场Ⅰ区的磁感应强度为B,方向竖直向上,左边界在水平段导轨的最左端;磁场Ⅱ区的磁感应强度为2B,方向竖直向下.质量均为m、电阻均为R的金属棒a、b垂直放置在导轨上(b在区域Ⅱ内),现将金属棒a从弯曲导轨上距水平段导轨高h处由静止释放,金属棒a、b始终垂直导轨且接触良好,重力加速度为g.则:
(1)求金属棒a刚进入磁场Ⅰ区时,金属棒b的加速度;
[答案],方向向左
[解析] a棒下滑过程中由机械能守恒
定律得mgh=m解得v0=
a棒刚进入磁场Ⅰ区时,有E=BLv0
此时通过a、b棒的感应电流I=
对b棒,F安=2BIL=
则a=,方向向左.
(2)设两磁场区足够大(即a、b分别在磁场Ⅰ、Ⅱ运动),回路中最多能产生的焦耳热有多少
[答案]
[解析] 当金属棒a进入磁场 Ⅰ 后 , a棒向右减速,b棒向左加速,最终达到稳定状态,
有BLv1=2BLv2,得v1=2v2
设向右为正方向,对金属棒a,由动量定理有-BLi·t=mv1-mv0
对金属棒b,由动量定理有-2BLi·t=-mv2-0 ,解得v1= ,v2=
根据能量守恒定律知,回路中产生的最多的焦耳热
Q=mgh-
2. 如图所示,在水平面内固定一足够长的光滑平行金属导轨ab-a'b'与cdef-c'd'e'f',b与c之间以及b'与c'之间分别通过一小段长度可忽略的绝缘光滑轨道平滑连接,其中abcd-a'b'c'd'部分的宽度为2d,ef-e'f'部分的宽度为d,导轨最左端a、a'之间连接有一带电的、电容为C的电容器和开关S,整个导轨所在空间存在方向竖直向上、磁感应强度大小为B的匀强磁场.开始时开关断开,质量为m,长度为d,阻值为R的金属棒N静止在导轨ef-e'f'部分上,质量为2m,长度为2d,电阻可忽略不计的金属棒M静止在导轨ab-a'b'部分上.现闭合开关S,电容器C通过金属棒M放电,金属棒M开始沿导轨向右运动,且离开ab-a'b'部分前的一段距离内金属棒M以速度大小v0匀速运动.不计导轨电阻,两金属棒运动过程中始终与导轨垂直且接触良好,金属棒M始终在abcd-a'b'c'd'部分运动,求:
(1)金属棒M刚滑上导轨cdef-c'd'e'f'部分时加速度的大小;
[答案]
[解析] 金属棒M刚滑上导轨cdef-c'd'e'f'部分时,回路中的电流大小为I1=
E=2Bdv0
由牛顿第二定律可知金属棒M的加速度大小为a=
解得a=
(2)电容器初始时的带电荷量;
[答案] +2Bdv0C
[解析] 闭合开关S,设金属棒M速度达到稳定前某时刻的电流为I,金属棒M受到的安培力大小为F=BI·2d
在一小段时间Δt内,由动量定理可得F·Δt=2m·Δv
通过金属棒M的电荷量为Δq=I·Δt
从闭合开关S到金属棒M速度达到稳定的过程中累加求和有Bq·2d=2mv0-0
金属棒M速度稳定时切割磁感线产生的电动势为 E'=B·2dv0
此时电容器剩余的电荷量为Q1=CE'
所以电容器初始时的带电荷量为Q=q+Q1=+2Bdv0C
(3)整个过程中金属棒N产生的焦耳热.
[答案] m
[解析] 金属棒M滑上导轨cdef-c'd'e'f'部分后,流过金属棒M和金属棒N的电流大小相等,当回路中的电流为0时,两金属棒速度达到稳定,此时有B·2dv1=Bdv2
从金属棒M滑上导轨cdef-c'd'e'f'部分到速度达到稳定的过程中,根据动量定理可知,对金属棒M有Bq'·2d=2mv0-2mv1
对金属棒N有Bq'd=mv2-0
由能量守恒定律可得·2m·2mm+Q热
解得Q热=m
1.如图甲所示,在光滑的水平面上有一质量、足够长的 形金属
导轨,导轨间距.一阻值 的细导体棒 垂直于导轨
放置,并被固定在水平面上的两立柱挡住,导体棒 与导轨间的动摩擦
因数,在、两端接有一理想电压表(图中未画出).在形导轨
边初始位置右侧存在垂直于导轨平面向下、磁感应强度大小 的匀
强磁场,在两立柱左侧 形导轨内存在方向水平向左、磁感应强度大小为
的匀强磁场.以形导轨的点初始位置为原点,以沿 方向为正方向,
建立坐标轴时,形导轨的边在沿轴正方向的外力 作用下从
静止开始运动,电压表测得电压与时间的关系如图乙所示.经过 时间,
撤去外力,直至形导轨静止.已知内外力做功 .不计其他
电阻,导体棒始终与导轨垂直,忽略导体棒 的重力.
(1) 求在内外力随时间 的变化规律;
[答案]
[解析] 根据法拉第电磁感应定律可知
由于只有导体棒有电阻,故、两端电压等于产生的感应电动势 .
由图像可知
联立得
根据速度与时间关系可知
由于忽略导体棒的重力,所以摩擦力
对形金属导轨,根据牛顿第二定律有
其中
联立解得
[解析] 由功能关系得
由于摩擦力与安培力的关系为,故
则
解得
(2) 求在整个运动过程中电路产生的焦耳热 ;
[答案]
(3) 写出在整个运动过程中形导轨的边的速度与位置 的函数关系式.
[答案] 见解析
[解析] 撤去外力的时刻为时,形导轨的边在 时间内
做匀加速直线运动,在 后做非匀变速直线运动.
①时,根据位移与速度关系可知
根据匀变速直线运动规律可知,时形导轨的 边的速度为
位移为
②时,形导轨的 边做非匀变速直线运动直到停止,由动量定
理得
其中
联立解得
当时,
综上所述,边的速度与位置 的函数关系式如下:
2.[2024·杭州模拟] 如图所示,固定
的一对长金属导轨间距为 ,
其水平部分与倾斜部分均足够长.导
轨的水平部分处于竖直向上的匀强磁
场中,磁感应强度大小为 ,其左侧
连接了电源 .导轨的倾斜部分倾角
且处于平行于斜面向上的匀
强磁场中,磁感应强度大小为 ,其
下方接有开关和电容 的电
容器,开始时开关断开、电容器不带
电.导轨上正对的、 两处各有一小
段用绝缘材料制成,长度不计.质量
均为 的导电杆甲、乙静
止在导轨上,均与导轨垂直,甲与导
轨间的摩擦不计,甲的电阻
, 乙的电阻 .某时
刻起电源 开始工作,输出恒定电流
,经 ,使甲运动到
、处,电源 立即停止工作.当甲
越过、 瞬间,再对其施加一个沿
导轨水平向右的恒力 ,此时
乙恰好开始运动. 已知 ,
不计除导电杆外所有电阻,不计回路
自身激发磁场,最大静摩擦力等于滑
动摩擦力, ,
.
(1) 求甲通过、 时的速度大小;
[答案]
[解析] 对甲导电杆进行分析,根据牛
顿第二定律有
根据运动学公式有
联立解得
(2) 求乙与倾斜导轨间的动摩擦因数;
[答案]
[解析] 甲导电杆刚刚通过、 时产生的
感应电动势
感应电流
根据右手定则可知,回路中电流方向为逆
时针,根据左手定则可知,乙导电杆所
受安培力方向垂直于斜面向上,大小为
此时乙导电杆恰好开始运动,有
联立解得
(3) 求电源 输出的总能量;
[答案]
[解析] 根据能量守恒定律可知,电源
输出的总能量
联立解得
(4) 为回收部分能量,闭合开关,其他条件不变,已知在甲通过、 后
内位移为,产生的焦耳热为 ,此时电容器已达到最大稳定电
压.当电容器电压为时,其储能为 .忽略电磁辐射,求此过程
中乙上产生的焦耳热.
[答案]
[解析] 甲导电杆越过、 后,在拉力作
用下,甲导电杆向右先做加速度减小的
加速运动,最后做匀速直线运动,匀速
运动时受力平衡,有
感应电流
对甲导电杆,根据动能定理有
根据功能关系有
其中
联立解得
同课章节目录
