2024-2025北师大九年级数学(下)二次函数题型分类训练(无答案)
文档属性
| 名称 | 2024-2025北师大九年级数学(下)二次函数题型分类训练(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 08:32:08 | ||
图片预览


文档简介
2024-2025北师大九年级数学二次函数题型分类训练
题型一:二次函数的定义
1.下列函数中,是二次函数的是( )
A.y=2x2+4x B.y=-3x C.y=mx2+nx+p D.y =错误!未定义书签。
2.y=(m-1)xm2 +1+5x-3是二次函数则m的值为( )
A.3 B.1 C.-1 D.2
3.若函数y=(m2+2m-7)x2+4x+5是关于x的二次函数,则m的取值范围为 。
4.若函数y=(m-2)xm -2+5x+1是关于的二次函数,则m的值为 。
题型二:二次函数的对称轴、顶点、最值
5.抛物线y=2x2+5x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.y=(x-5)2+2的对称轴是直线( )
A.x=-5 B.x=5 C.y=-5 D.y=5
7.若直线y=ax+b不经过二、四象限,则抛物线y=ax2+bx+c( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴是y轴
C.开口向下,对称轴平行于y轴 D.开口向上,对称轴平行于y轴
8.抛物线y=x2-3x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.若抛物线y=ax2-6x经过点(2,0),则抛物线顶点到坐标原点的距离为( )
A. B. C. D.
10.若直线y=ax+b不经过二、四象限,则抛物线y=ax2+bx+c( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴是y轴
C.开口向下,对称轴平行于y轴 D.开口向上,对称轴平行于y轴
11.若抛物线y=ax2+bx+c(a≠0)的图象与抛物线y=x2+4x-1的图象关于y轴对称,则函数y=ax2+bx+c
的解析式为 .
12.若抛物线y=x2+bx+c与y轴交于点A,与x轴正半轴交于B,C两点,且BC=4,S△ABC=6,则b=______.
13.抛物y=x2+bx+c线的顶点坐标为(6,2),则b= ,c= .
14.已知抛物线y=x2+(m-1)x-的顶点的横坐标是2,求m的值.
题型三:二次函数的图象和性质
15.函数y=x2-6x+5经过的象限是( )
A.一、二、三象限 B.一、二象限 C.三、四象限 D.一、二、四象限
16.已知二次函数、、,它们的图像开口由小到大的顺序是( )
A、 B、 C、 D、
17.已知y=x2-6x-4,当函数值y随x的增大而减小时,x的取值范围是( )
A.x<3 B.x>3 C.x>-3 D.-3<x<4
18.二次函数y=a(x+k)2+k,当k取不同的实数值时,图象顶点所在的直线是( )
A.y=x B.x轴 C.y=-x D.y轴
19.正比例函数y=kx的图象经过二、四象限,则抛物线y=kx2-2x+k2的大致图象是( )
20.如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B.14 C.8或14 D.-8或-14
21.抛物线y=2x2-12x+25的开口方向是 ,顶点坐标是 。
22.试写出一个开口方向向上,对称轴为直线x=-1,且与y轴的交点坐标为(0,4)的抛物线的解析式 。
23.二次函数y=a(x-h)2的图象如图所示,已知a=,OA=OC,试求该抛物线的解析式。
题型四:二次函数的增减性
24.二次函数y=2x2-8x+5,当x>2时,y随x的增大而 ;当x<2时,y随x的增大而 ;当x=2时,函数有最 值是 。
25.已知函数y=2x2-mx+7,当x>-2时,y随x的增大而增大;当x<-2时,y随x的增大而减少;则x=1时,y的值为 。
26.已知二次函数y=x2-(m+1)x+1,当x≥1时,y随x的增大而增大,则m的取值范围是 .
27.若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系为 .
题型五:二次函数的平移
28.抛物线可以通过将抛物线y= 向 平移 个单位、再向 平移 个单位得到。
29.抛物线y=-x2向左平移3个单位,再向下平移4个单位,所得到的抛物线的关系式为 。
30.将抛物线y=3x2 ,可以得到y=3(x-6}2-8。
31.将抛物线y=ax2+bx+c向上平移1个单位,再向右平移1个单位,得到y=2x2-4x-1则a= ,b= ,c= .
32.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(5,-2),那么移动后的抛物线的关系式为 .
题型五:函数的交点及对称
33.抛物线y=x2+6x+5与直线y=2x+8的交点坐标为 。
34.直线y=3x+1与抛物线y=x2+4x+3的图象有 个交点。
35.抛物线y=2x2-4x关于y轴对称的抛物线的关系式为 。
36.抛物线y=ax2+bx+c关于x轴对称的抛物线为y=2x2-4x+3,则a= b= c= 。
37. 抛物线y=ax2+bx+c 经过A (-3,6),B(1,6)两点,则抛物线对称轴经过的点的坐标是 。
题型六:函数的图象特征与a、b、c的关系
38.已知抛物线y=ax2+bx+c的图象如右图所示,则a、b、c的符号为( )
A.a>0,b>0,c>0 B.a>0,b>0,c=0 C.a>0,b<0,c=0 D.a>0,b<0,c<0
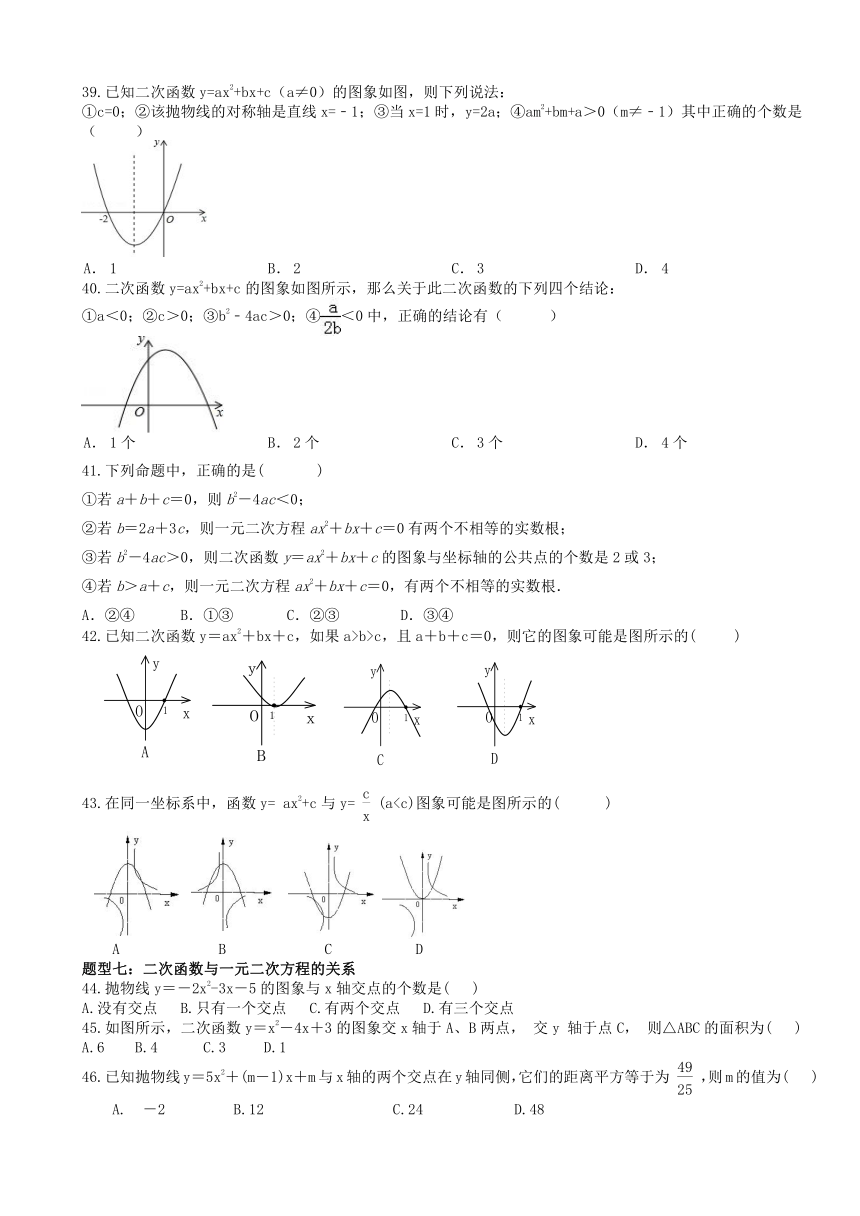
39.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:
①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1)其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
40.二次函数y=ax2+bx+c的图象如图所示,那么关于此二次函数的下列四个结论:
①a<0;②c>0;③b2﹣4ac>0;④<0中,正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
41.下列命题中,正确的是( )
①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b2-4ac>0,则二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是2或3;
④若b>a+c,则一元二次方程ax2+bx+c=0,有两个不相等的实数根.
A.②④ B.①③ C.②③ D.③④
42.已知二次函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是图所示的( )
43.在同一坐标系中,函数y= ax2+c与y= (aA B C D
题型七:二次函数与一元二次方程的关系
44.抛物线y=-2x2-3x-5的图象与x轴交点的个数是( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
45.如图所示,二次函数y=x2-4x+3的图象交x轴于A、B两点, 交y 轴于点C, 则△ABC的面积为( )
A.6 B.4 C.3 D.1
46.已知抛物线y=5x2+(m-1)x+m与x轴的两个交点在y轴同侧,它们的距离平方等于为 ,则m的值为( )
-2 B.12 C.24 D.48
47.如果二次函数y=x2+5x+c图象与x轴没有交点,其中c为整数,则c= (写一个即可)
48.二次函数y=x2-2x-8图象与x轴交点之间的距离为
49.若二次函数y=(m+3)x2+2(m-2)x+m的图象全部在x轴的上方,则m的取值范围是
50.已知抛物线y=x2-2x-8,
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点为A、B,且它的顶点为P,求△ABP的面积。
题型八:函数解析式的求法
51.已知二次函数的图象经过A(0,2)、B(1,3)、C(-1,5)三点,求该二次函数的解析式。
52.已知抛物线过A(1,0)和B(6,0)两点,交y轴于C点且BC=5,求该二次函数的解析式。
53.y=ax2+bx+c图象与x轴交于A、B与y轴交于C,OA=2,OB=1 ,OC=1,求函数解析式
54.知二次函数图象顶点坐标(-3,)且图象过点(2,),求二次函数解析式。
55.抛物线y= (k2-2)x2+m-4kx的对称轴是直线x=2,且它的最低点在直线y=-+2上,求函数解析式。
题型九:以二次函数为基架的综合题
56. 二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x= -1。
①求函数解析式;②若图象与x轴交于A、B(A在B左)与y轴交于C,顶点D,求四边形ABCD的面积。
57.已知:抛物线与X轴分别交于A、B两点(点A在B的左边),点P为抛物线的顶点,(1)若抛物线的顶点在直线上,求抛物线的解析式;
(2)若AP∶BP∶AB=1∶1∶,求抛物线的解析式。
58.抛物线与x轴交点为A,B,(A在B左侧)顶点为C.与Y轴交于点D,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
59.在轴上方的抛物线上是否存在一点M,过M作MG轴点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
题型十:二次函数的应用
60.如图,在一个矩形空地ABCD上修建一个矩形花坛AMPQ,要求点M在AB上,点Q在AD上,点P在对角线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
(1)求S与x的函数关系式;
(2)当x为何值时,S有最大值?请求出最大值.
61.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
62.某商场批单价为25元的旅游鞋。为确定 一个最佳的销售价格,在试销期采用多种价格进性销售,经试验发现:按每双30元的价格销售时,每天能卖出60双;按每双32元的价格销售时,每天能卖出52双,假定每天售出鞋的数量Y(双)是销售单位X的一次函数。
(1)求Y与X之间的函数关系式;
(2)在鞋不积压,且不考虑其它因素的情况下,求出每天的销售利润W(元)与销售单价X之间的函数关系式;
(3)销售价格定为多少元时,每天获得的销售利润最多?是多少?
63.宿州市某工艺厂为了打开市场,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,其中工艺品的销售单价x(元∕件)
与每天销售量y(件)之间满足如图所示关系.
(1)请根据图象直接写出当销售单价定为30元和40元时相应的日销售量;
(2)①试求出y与x之间的函数关系式;
②若物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)。
64.某商场批单价为25元的旅游鞋。为确定 一个最佳的销售价格,在试销期采用多种价格进性销售,经试验发现:按每双30元的价格销售时,每天能卖出60双;按每双32元的价格销售时,每天能卖出52双,假定每天售出鞋的数量Y(双)是销售单位X的一次函数。
(1)求Y与X之间的函数关系式;
(2)在鞋不积压,且不考虑其它因素的情况下,求出每天的销售利润W(元)与销售单价X之间的函数关系式;
(3)销售价格定为多少元时,每天获得的销售利润最多?是多少?
题型一:二次函数的定义
1.下列函数中,是二次函数的是( )
A.y=2x2+4x B.y=-3x C.y=mx2+nx+p D.y =错误!未定义书签。
2.y=(m-1)xm2 +1+5x-3是二次函数则m的值为( )
A.3 B.1 C.-1 D.2
3.若函数y=(m2+2m-7)x2+4x+5是关于x的二次函数,则m的取值范围为 。
4.若函数y=(m-2)xm -2+5x+1是关于的二次函数,则m的值为 。
题型二:二次函数的对称轴、顶点、最值
5.抛物线y=2x2+5x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.y=(x-5)2+2的对称轴是直线( )
A.x=-5 B.x=5 C.y=-5 D.y=5
7.若直线y=ax+b不经过二、四象限,则抛物线y=ax2+bx+c( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴是y轴
C.开口向下,对称轴平行于y轴 D.开口向上,对称轴平行于y轴
8.抛物线y=x2-3x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.若抛物线y=ax2-6x经过点(2,0),则抛物线顶点到坐标原点的距离为( )
A. B. C. D.
10.若直线y=ax+b不经过二、四象限,则抛物线y=ax2+bx+c( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴是y轴
C.开口向下,对称轴平行于y轴 D.开口向上,对称轴平行于y轴
11.若抛物线y=ax2+bx+c(a≠0)的图象与抛物线y=x2+4x-1的图象关于y轴对称,则函数y=ax2+bx+c
的解析式为 .
12.若抛物线y=x2+bx+c与y轴交于点A,与x轴正半轴交于B,C两点,且BC=4,S△ABC=6,则b=______.
13.抛物y=x2+bx+c线的顶点坐标为(6,2),则b= ,c= .
14.已知抛物线y=x2+(m-1)x-的顶点的横坐标是2,求m的值.
题型三:二次函数的图象和性质
15.函数y=x2-6x+5经过的象限是( )
A.一、二、三象限 B.一、二象限 C.三、四象限 D.一、二、四象限
16.已知二次函数、、,它们的图像开口由小到大的顺序是( )
A、 B、 C、 D、
17.已知y=x2-6x-4,当函数值y随x的增大而减小时,x的取值范围是( )
A.x<3 B.x>3 C.x>-3 D.-3<x<4
18.二次函数y=a(x+k)2+k,当k取不同的实数值时,图象顶点所在的直线是( )
A.y=x B.x轴 C.y=-x D.y轴
19.正比例函数y=kx的图象经过二、四象限,则抛物线y=kx2-2x+k2的大致图象是( )
20.如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B.14 C.8或14 D.-8或-14
21.抛物线y=2x2-12x+25的开口方向是 ,顶点坐标是 。
22.试写出一个开口方向向上,对称轴为直线x=-1,且与y轴的交点坐标为(0,4)的抛物线的解析式 。
23.二次函数y=a(x-h)2的图象如图所示,已知a=,OA=OC,试求该抛物线的解析式。
题型四:二次函数的增减性
24.二次函数y=2x2-8x+5,当x>2时,y随x的增大而 ;当x<2时,y随x的增大而 ;当x=2时,函数有最 值是 。
25.已知函数y=2x2-mx+7,当x>-2时,y随x的增大而增大;当x<-2时,y随x的增大而减少;则x=1时,y的值为 。
26.已知二次函数y=x2-(m+1)x+1,当x≥1时,y随x的增大而增大,则m的取值范围是 .
27.若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系为 .
题型五:二次函数的平移
28.抛物线可以通过将抛物线y= 向 平移 个单位、再向 平移 个单位得到。
29.抛物线y=-x2向左平移3个单位,再向下平移4个单位,所得到的抛物线的关系式为 。
30.将抛物线y=3x2 ,可以得到y=3(x-6}2-8。
31.将抛物线y=ax2+bx+c向上平移1个单位,再向右平移1个单位,得到y=2x2-4x-1则a= ,b= ,c= .
32.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(5,-2),那么移动后的抛物线的关系式为 .
题型五:函数的交点及对称
33.抛物线y=x2+6x+5与直线y=2x+8的交点坐标为 。
34.直线y=3x+1与抛物线y=x2+4x+3的图象有 个交点。
35.抛物线y=2x2-4x关于y轴对称的抛物线的关系式为 。
36.抛物线y=ax2+bx+c关于x轴对称的抛物线为y=2x2-4x+3,则a= b= c= 。
37. 抛物线y=ax2+bx+c 经过A (-3,6),B(1,6)两点,则抛物线对称轴经过的点的坐标是 。
题型六:函数的图象特征与a、b、c的关系
38.已知抛物线y=ax2+bx+c的图象如右图所示,则a、b、c的符号为( )
A.a>0,b>0,c>0 B.a>0,b>0,c=0 C.a>0,b<0,c=0 D.a>0,b<0,c<0
39.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:
①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1)其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
40.二次函数y=ax2+bx+c的图象如图所示,那么关于此二次函数的下列四个结论:
①a<0;②c>0;③b2﹣4ac>0;④<0中,正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
41.下列命题中,正确的是( )
①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b2-4ac>0,则二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是2或3;
④若b>a+c,则一元二次方程ax2+bx+c=0,有两个不相等的实数根.
A.②④ B.①③ C.②③ D.③④
42.已知二次函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是图所示的( )
43.在同一坐标系中,函数y= ax2+c与y= (a
题型七:二次函数与一元二次方程的关系
44.抛物线y=-2x2-3x-5的图象与x轴交点的个数是( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
45.如图所示,二次函数y=x2-4x+3的图象交x轴于A、B两点, 交y 轴于点C, 则△ABC的面积为( )
A.6 B.4 C.3 D.1
46.已知抛物线y=5x2+(m-1)x+m与x轴的两个交点在y轴同侧,它们的距离平方等于为 ,则m的值为( )
-2 B.12 C.24 D.48
47.如果二次函数y=x2+5x+c图象与x轴没有交点,其中c为整数,则c= (写一个即可)
48.二次函数y=x2-2x-8图象与x轴交点之间的距离为
49.若二次函数y=(m+3)x2+2(m-2)x+m的图象全部在x轴的上方,则m的取值范围是
50.已知抛物线y=x2-2x-8,
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点为A、B,且它的顶点为P,求△ABP的面积。
题型八:函数解析式的求法
51.已知二次函数的图象经过A(0,2)、B(1,3)、C(-1,5)三点,求该二次函数的解析式。
52.已知抛物线过A(1,0)和B(6,0)两点,交y轴于C点且BC=5,求该二次函数的解析式。
53.y=ax2+bx+c图象与x轴交于A、B与y轴交于C,OA=2,OB=1 ,OC=1,求函数解析式
54.知二次函数图象顶点坐标(-3,)且图象过点(2,),求二次函数解析式。
55.抛物线y= (k2-2)x2+m-4kx的对称轴是直线x=2,且它的最低点在直线y=-+2上,求函数解析式。
题型九:以二次函数为基架的综合题
56. 二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x= -1。
①求函数解析式;②若图象与x轴交于A、B(A在B左)与y轴交于C,顶点D,求四边形ABCD的面积。
57.已知:抛物线与X轴分别交于A、B两点(点A在B的左边),点P为抛物线的顶点,(1)若抛物线的顶点在直线上,求抛物线的解析式;
(2)若AP∶BP∶AB=1∶1∶,求抛物线的解析式。
58.抛物线与x轴交点为A,B,(A在B左侧)顶点为C.与Y轴交于点D,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
59.在轴上方的抛物线上是否存在一点M,过M作MG轴点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
题型十:二次函数的应用
60.如图,在一个矩形空地ABCD上修建一个矩形花坛AMPQ,要求点M在AB上,点Q在AD上,点P在对角线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
(1)求S与x的函数关系式;
(2)当x为何值时,S有最大值?请求出最大值.
61.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
62.某商场批单价为25元的旅游鞋。为确定 一个最佳的销售价格,在试销期采用多种价格进性销售,经试验发现:按每双30元的价格销售时,每天能卖出60双;按每双32元的价格销售时,每天能卖出52双,假定每天售出鞋的数量Y(双)是销售单位X的一次函数。
(1)求Y与X之间的函数关系式;
(2)在鞋不积压,且不考虑其它因素的情况下,求出每天的销售利润W(元)与销售单价X之间的函数关系式;
(3)销售价格定为多少元时,每天获得的销售利润最多?是多少?
63.宿州市某工艺厂为了打开市场,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,其中工艺品的销售单价x(元∕件)
与每天销售量y(件)之间满足如图所示关系.
(1)请根据图象直接写出当销售单价定为30元和40元时相应的日销售量;
(2)①试求出y与x之间的函数关系式;
②若物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)。
64.某商场批单价为25元的旅游鞋。为确定 一个最佳的销售价格,在试销期采用多种价格进性销售,经试验发现:按每双30元的价格销售时,每天能卖出60双;按每双32元的价格销售时,每天能卖出52双,假定每天售出鞋的数量Y(双)是销售单位X的一次函数。
(1)求Y与X之间的函数关系式;
(2)在鞋不积压,且不考虑其它因素的情况下,求出每天的销售利润W(元)与销售单价X之间的函数关系式;
(3)销售价格定为多少元时,每天获得的销售利润最多?是多少?
