2024-2025学年北京市平谷五中高二(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年北京市平谷五中高二(上)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 101.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 22:10:15 | ||
图片预览



文档简介
2024-2025学年北京市平谷五中高二(上)期中数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知,,则与的夹角为( )
A. B. C. D.
3.下列命题中,正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
4.从甲、乙、丙、丁四人任选两人参加问卷调查,则甲被选中的概率是( )
A. B. C. D.
5.为深入贯彻落实国务院办公厅关于强化学校体育促进学生身心健康全面发展的意见,我市提出:到年,全市义务教育阶段学生体质健康合格率达到,基础教育阶段学生优秀率达到以上某学校现有小学和初中学生共人,为了解学生的体质健康合格情况,决定采用分层抽样的方法从全校学生中抽取一个容量为的样本,其中被抽到的初中学生人数为,那么这所学校的初中学生人数为( )
A. B. C. D.
6.已知两条不同的直线,,两个不同的平面,,则下列说法正确的是( )
A. 若,,,则 B. 若,,则
C. 若,,,则 D. 若,,,则
7.甲、乙两人射击,甲的命中率为,乙的命中率为,如果甲、乙两人各射击一次,恰有一人命中的概率为( )
A. B. C. D.
8.如图,正方体的棱长为,,分别为棱,上的动点,那么三棱锥的体积为( )
A.
B.
C.
D.
9.有个相同的球,分别标有数字,,,,,,从中有放回的随机取两次,每次取个球,甲表示事件“第一次取出的球的数字是”,乙表示事件“第二次取出的球的数字是”,丙表示事件“两次取出的球的数字之和是”,丁表示事件“两次取出的球的数字之和是”,则( )
A. 甲与丙相互独立 B. 甲与丁相互独立 C. 乙与丙相互独立 D. 丙与丁相互独立
10.正多面体也称柏拉图立体,被誉为最有规律的立体结构,是所有面都只由一种正多边形构成的多面体各面都是全等的正多边形数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体如图,已知一个正八面体的棱长为,,分别为棱,的中点,则直线和夹角的余弦值为( )
A.
B.
C.
D.
二、填空题:本题共8小题,每小题5分,共40分。
11.函数的定义域为______.
12.复数其中为虚数单位的虚部为______.
13.已知空间向量,,且与是共线向量,则实数的值为______.
14.正四棱锥底面边长为,侧棱长为,则其体积为______.
15.若,是两条不同的直线,,是两个不同平面,,则“”是“”的____条件.
16.某高校调查了名学生每周的自习时间单位:小时,制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,根据直方图,这名学生中每周的自习时间不少于小时的人数是______.
17.已知实验女排和育才女排两队进行比赛,在一局比赛中实验女排获胜的概率是,没有平局.若采用三局两胜制,即先胜两局者获胜且比赛结束,则实验女排获胜的概率为______.
18.如图,在棱长为的正方体中,为棱上的动点且不与重合,为线段的中点给出下列四个命题:
三棱锥的体积为;
;
的面积为定值;
四棱锥是正四棱锥.
其中所有正确命题的序号是 .
三、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,在四棱锥中,底面是菱形,平面,为的中点.
Ⅰ求证:平面;
Ⅱ求证:平面.
20.本小题分
如图,三棱锥中,,平面平面,点是棱的中点,再从条件、条件这两个条件中选择一个作为已知.
求平面与平面的夹角的余弦值.
求点到面的距离.
条件:;
条件:直线与平面所成角为.
注:如果选择条件和条件分别解答,按第一个解答计分.
21.本小题分
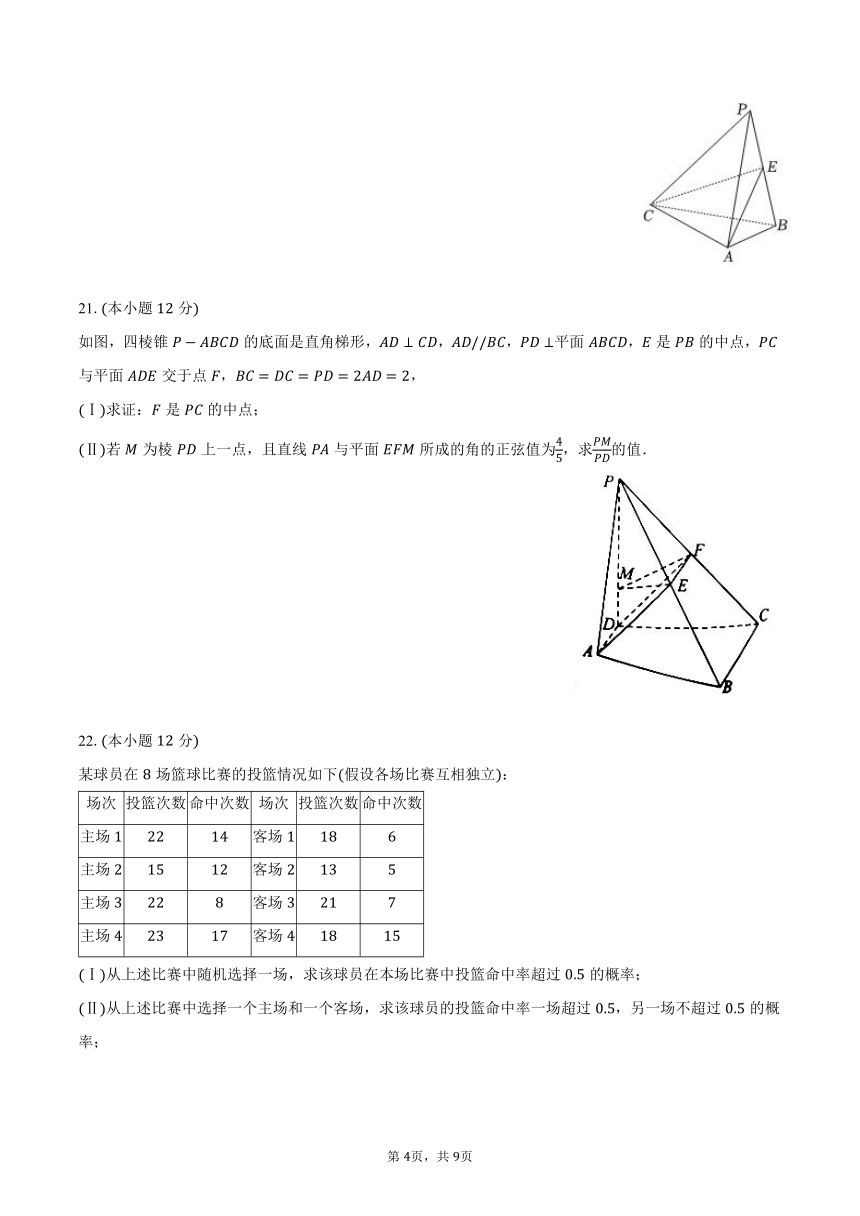
如图,四棱锥的底面是直角梯形,,,平面,是的中点,与平面交于点,,
Ⅰ求证:是的中点;
Ⅱ若为棱上一点,且直线与平面所成的角的正弦值为,求的值.
22.本小题分
某球员在场篮球比赛的投篮情况如下假设各场比赛互相独立:
场次 投篮次数 命中次数 场次 投篮次数 命中次数
主场 客场
主场 客场
主场 客场
主场 客场
Ⅰ从上述比赛中随机选择一场,求该球员在本场比赛中投篮命中率超过的概率;
Ⅱ从上述比赛中选择一个主场和一个客场,求该球员的投篮命中率一场超过,另一场不超过的概率;
Ⅲ记是表中场命中率的平均数,是表中个主场命中率的平均数,是表中个客场命中率的平均数,比较的大小只需写出结论
23.本小题分
手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间为了解,两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取,两个型号的手机各台,在相同条件下进行测试,统计结果如下:
手机编号
型待机时间
型待机时间
已知,两个型号被测试手机待机时间的平均值相等.
求的值;
从被测试的手机中随机抽取,型号手机各台,求至少有台的待机时间超过小时的概率.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.既不充分也不必要
16.
17.
18.
19.证明:Ⅰ因为底面是菱形,所以,
又因为平面,平面,
所以,而,
可证得:平面;
Ⅱ设,连接,因为底面是菱形,
所以为的中点,为的中点,所以为的中位线,
所以,
又因为平面,平面,
可证得:平面.
20.解:取中点为,连接,,
因为,所以是等边三角形,则,
又平面平面,平面平面,平面,
所以平面,因为平面,则.
若选条件:因为,,结合,可得.
又因为,则是以为,为的直角三角形.
若选条件:因为平面,所以即为直线与平面所成角,
因为,则为等腰直角三角形,因为,可得,
又因为,则是以为,为的直角三角形.
即,,是等边三角形.
如图延长,建立以为原点的空间直角坐标系.
则.
所以,
设平面法向量为,则,,
所以,取.
由题知,平面的一个法向量为,
设平面与平面的夹角为,
则;
由可得,
设平面法向量为,则,,
所以,取,
又,
则求点到面的距离.
21.解:Ⅰ证明:,平面,平面,
平面,
平面,平面平面,
,,
点是的中点,点是的中点.
Ⅱ平面,,平面,
,,由,建立如图所示的空间直角坐标系,
则,,,,,,
,,,,
设,,
,
设平面的一个法向量,
则,取,得,
,
设直线与平面所成角为,
则,
解得或,
的值为或.
22.解:Ⅰ有题意可知在场比赛中,该球员投篮命中率超过的有场,
分别是主场,主场,主场,客场.
所以在随机选择的一场比赛中,该球员投篮命中率超过的概率为;
Ⅱ设事件为“在随机选择的一场主场比赛中,该球员的投篮命中率超过”,
事件为“在随机选择的一场客场比赛中,该球员的投篮命中率超过”
事件为“在随机选择的一个主场和一个客场中,该球员的投篮命中率一场超过,一场不超过”.
则相互独立.
由题意可知,,,,
故;
Ⅲ由于主场命中的次数更多,所以.
23.解:现从某卖场库存手机中随机抽取,两个型号的手机各台,在相同条件下进行测试,
依题意,,,
由,解得,所以的值.
设型号手机为,,,,,型号手机为,,,,,“至少有台的待机时间超过小时”为事件,
从被测试的手机中随机抽取,型号手机各台,不同的抽取方法有种,
抽取的两台手机待机时间都不超过小时的选法有:,,,,共种,
因此,,
所以至少有台的待机时间超过小时的概率是.
第1页,共1页
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知,,则与的夹角为( )
A. B. C. D.
3.下列命题中,正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
4.从甲、乙、丙、丁四人任选两人参加问卷调查,则甲被选中的概率是( )
A. B. C. D.
5.为深入贯彻落实国务院办公厅关于强化学校体育促进学生身心健康全面发展的意见,我市提出:到年,全市义务教育阶段学生体质健康合格率达到,基础教育阶段学生优秀率达到以上某学校现有小学和初中学生共人,为了解学生的体质健康合格情况,决定采用分层抽样的方法从全校学生中抽取一个容量为的样本,其中被抽到的初中学生人数为,那么这所学校的初中学生人数为( )
A. B. C. D.
6.已知两条不同的直线,,两个不同的平面,,则下列说法正确的是( )
A. 若,,,则 B. 若,,则
C. 若,,,则 D. 若,,,则
7.甲、乙两人射击,甲的命中率为,乙的命中率为,如果甲、乙两人各射击一次,恰有一人命中的概率为( )
A. B. C. D.
8.如图,正方体的棱长为,,分别为棱,上的动点,那么三棱锥的体积为( )
A.
B.
C.
D.
9.有个相同的球,分别标有数字,,,,,,从中有放回的随机取两次,每次取个球,甲表示事件“第一次取出的球的数字是”,乙表示事件“第二次取出的球的数字是”,丙表示事件“两次取出的球的数字之和是”,丁表示事件“两次取出的球的数字之和是”,则( )
A. 甲与丙相互独立 B. 甲与丁相互独立 C. 乙与丙相互独立 D. 丙与丁相互独立
10.正多面体也称柏拉图立体,被誉为最有规律的立体结构,是所有面都只由一种正多边形构成的多面体各面都是全等的正多边形数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体如图,已知一个正八面体的棱长为,,分别为棱,的中点,则直线和夹角的余弦值为( )
A.
B.
C.
D.
二、填空题:本题共8小题,每小题5分,共40分。
11.函数的定义域为______.
12.复数其中为虚数单位的虚部为______.
13.已知空间向量,,且与是共线向量,则实数的值为______.
14.正四棱锥底面边长为,侧棱长为,则其体积为______.
15.若,是两条不同的直线,,是两个不同平面,,则“”是“”的____条件.
16.某高校调查了名学生每周的自习时间单位:小时,制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,根据直方图,这名学生中每周的自习时间不少于小时的人数是______.
17.已知实验女排和育才女排两队进行比赛,在一局比赛中实验女排获胜的概率是,没有平局.若采用三局两胜制,即先胜两局者获胜且比赛结束,则实验女排获胜的概率为______.
18.如图,在棱长为的正方体中,为棱上的动点且不与重合,为线段的中点给出下列四个命题:
三棱锥的体积为;
;
的面积为定值;
四棱锥是正四棱锥.
其中所有正确命题的序号是 .
三、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,在四棱锥中,底面是菱形,平面,为的中点.
Ⅰ求证:平面;
Ⅱ求证:平面.
20.本小题分
如图,三棱锥中,,平面平面,点是棱的中点,再从条件、条件这两个条件中选择一个作为已知.
求平面与平面的夹角的余弦值.
求点到面的距离.
条件:;
条件:直线与平面所成角为.
注:如果选择条件和条件分别解答,按第一个解答计分.
21.本小题分
如图,四棱锥的底面是直角梯形,,,平面,是的中点,与平面交于点,,
Ⅰ求证:是的中点;
Ⅱ若为棱上一点,且直线与平面所成的角的正弦值为,求的值.
22.本小题分
某球员在场篮球比赛的投篮情况如下假设各场比赛互相独立:
场次 投篮次数 命中次数 场次 投篮次数 命中次数
主场 客场
主场 客场
主场 客场
主场 客场
Ⅰ从上述比赛中随机选择一场,求该球员在本场比赛中投篮命中率超过的概率;
Ⅱ从上述比赛中选择一个主场和一个客场,求该球员的投篮命中率一场超过,另一场不超过的概率;
Ⅲ记是表中场命中率的平均数,是表中个主场命中率的平均数,是表中个客场命中率的平均数,比较的大小只需写出结论
23.本小题分
手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间为了解,两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取,两个型号的手机各台,在相同条件下进行测试,统计结果如下:
手机编号
型待机时间
型待机时间
已知,两个型号被测试手机待机时间的平均值相等.
求的值;
从被测试的手机中随机抽取,型号手机各台,求至少有台的待机时间超过小时的概率.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.既不充分也不必要
16.
17.
18.
19.证明:Ⅰ因为底面是菱形,所以,
又因为平面,平面,
所以,而,
可证得:平面;
Ⅱ设,连接,因为底面是菱形,
所以为的中点,为的中点,所以为的中位线,
所以,
又因为平面,平面,
可证得:平面.
20.解:取中点为,连接,,
因为,所以是等边三角形,则,
又平面平面,平面平面,平面,
所以平面,因为平面,则.
若选条件:因为,,结合,可得.
又因为,则是以为,为的直角三角形.
若选条件:因为平面,所以即为直线与平面所成角,
因为,则为等腰直角三角形,因为,可得,
又因为,则是以为,为的直角三角形.
即,,是等边三角形.
如图延长,建立以为原点的空间直角坐标系.
则.
所以,
设平面法向量为,则,,
所以,取.
由题知,平面的一个法向量为,
设平面与平面的夹角为,
则;
由可得,
设平面法向量为,则,,
所以,取,
又,
则求点到面的距离.
21.解:Ⅰ证明:,平面,平面,
平面,
平面,平面平面,
,,
点是的中点,点是的中点.
Ⅱ平面,,平面,
,,由,建立如图所示的空间直角坐标系,
则,,,,,,
,,,,
设,,
,
设平面的一个法向量,
则,取,得,
,
设直线与平面所成角为,
则,
解得或,
的值为或.
22.解:Ⅰ有题意可知在场比赛中,该球员投篮命中率超过的有场,
分别是主场,主场,主场,客场.
所以在随机选择的一场比赛中,该球员投篮命中率超过的概率为;
Ⅱ设事件为“在随机选择的一场主场比赛中,该球员的投篮命中率超过”,
事件为“在随机选择的一场客场比赛中,该球员的投篮命中率超过”
事件为“在随机选择的一个主场和一个客场中,该球员的投篮命中率一场超过,一场不超过”.
则相互独立.
由题意可知,,,,
故;
Ⅲ由于主场命中的次数更多,所以.
23.解:现从某卖场库存手机中随机抽取,两个型号的手机各台,在相同条件下进行测试,
依题意,,,
由,解得,所以的值.
设型号手机为,,,,,型号手机为,,,,,“至少有台的待机时间超过小时”为事件,
从被测试的手机中随机抽取,型号手机各台,不同的抽取方法有种,
抽取的两台手机待机时间都不超过小时的选法有:,,,,共种,
因此,,
所以至少有台的待机时间超过小时的概率是.
第1页,共1页
同课章节目录
