人教版九年级数学下名师点拨与训练第28章 锐角三角函数29.1 投影
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第28章 锐角三角函数29.1 投影 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.1 投影
学习目标:
1、理解投影的有关概念,能根据光线的方向辨认物体的投影。
2、理解平行投影和中心投影的区别与联系。
3、理解正投影概念,理解现实生活中影子的现象,学会用数学知识尝试解答。
学习重点:理解平行投影、中心投影、正投影的特征。
学习难点:在投影面上画出平面图形的平行投影、中心投影、正投影。
老师告诉你
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:1.线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
2.平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
一、知识点拨
知识点1 、 平行投影
1.投影的概念:
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面
2.平行投影:由平行光线所形成的投影称为平行投影.
注意:平行投影中物体与投影面平行时的投影是全等的.
判断投影是平行投影的方法是看光线是否是平行的.如果光线是平行的,所得到的投影就是平行投影.
【新知导学】
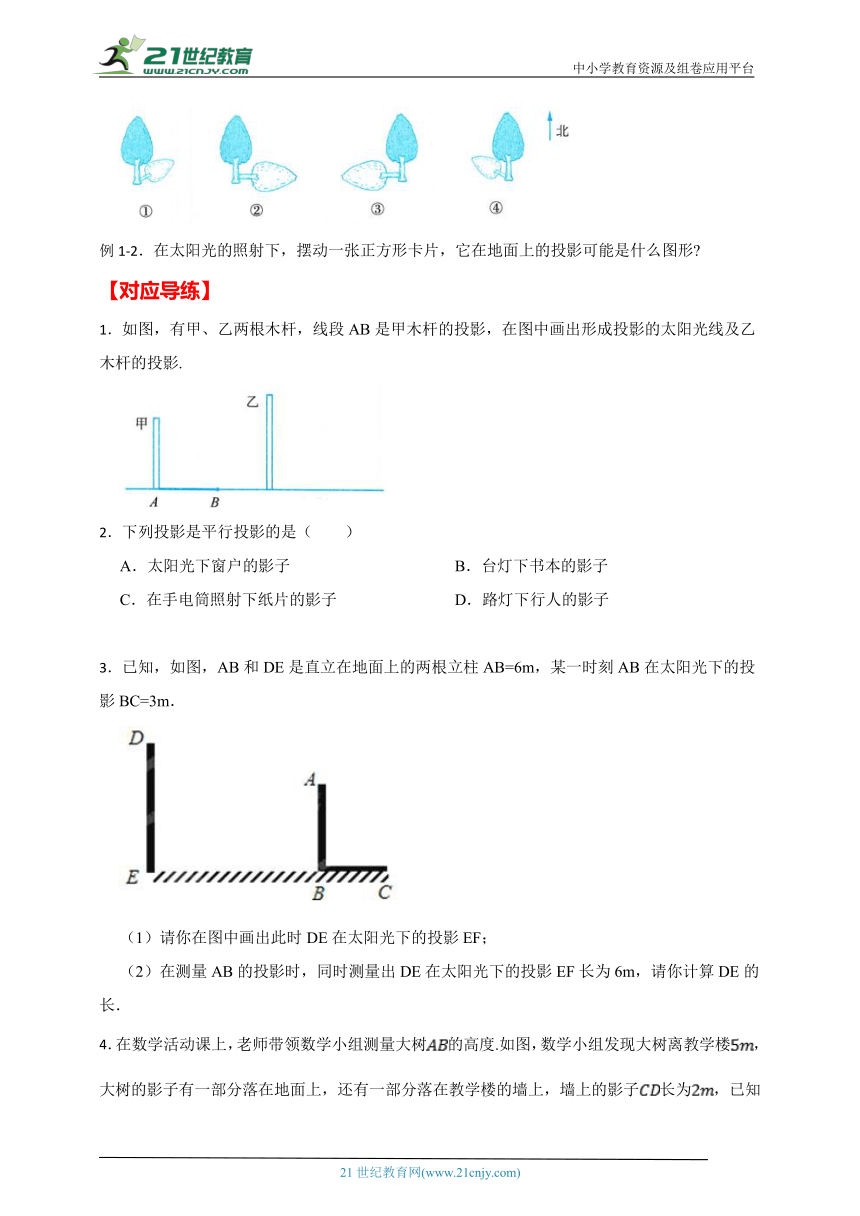
例1-1.下面四幅图是某校园内一棵小树不同时刻在太阳光下的影子,按照时间的先后顺序排列,是 .
例1-2.在太阳光的照射下,摆动一张正方形卡片,它在地面上的投影可能是什么图形
【对应导练】
1.如图,有甲、乙两根木杆,线段AB是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.
2.下列投影是平行投影的是( )
A.太阳光下窗户的影子 B.台灯下书本的影子
C.在手电筒照射下纸片的影子 D.路灯下行人的影子
3.已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
(1)请你在图中画出此时DE在太阳光下的投影EF;
(2)在测量AB的投影时,同时测量出DE在太阳光下的投影EF长为6m,请你计算DE的长.
4.在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼,大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为,已知此时高的竹竿在水平地面上的影子长,那么这棵大树高度是多少?
知识点2 、中心投影
1.中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.
2.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
3.判断投影是中心投影的方法是看光线是否相交于一点,如果光线是相交于一点,那么所得到的投影就是中心投影。
4.视点、视角和盲区
(1)把观察者所处的位置定为一点,叫视点.
(2)人眼到视平面的距离视固定的(视距),视平面左右两个边缘到人眼的连线得到的角度就是视角.
(3)盲区:视线到达不了的区域为盲区
【新知导学】
例2-1.下列现象属于中心投影的有( )
①小孔成像; ②皮影戏;③手影; ④放电影.
A.1个 B.2个 C.3个 D.4个
例2-2.某公园一角有一盏地面射灯照在一棵树上,树的影子投在墙上.已知树高1m,树与墙之间的距离为10m,与射灯之间的距离为5m.求树在墙上的影长.
【对应导练】
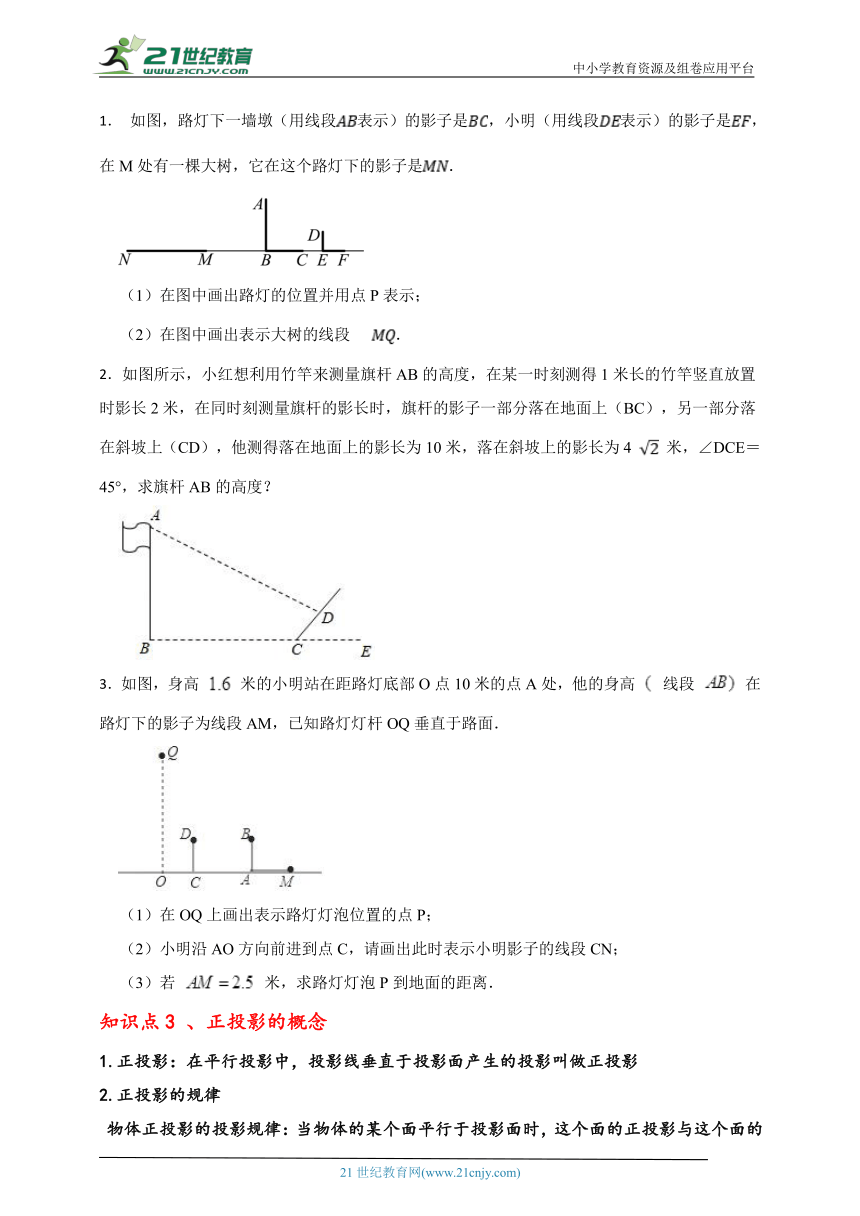
1. 如图,路灯下一墙墩(用线段表示)的影子是,小明(用线段表示)的影子是,在M处有一棵大树,它在这个路灯下的影子是.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段.
2.如图所示,小红想利用竹竿来测量旗杆AB的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为4 米,∠DCE=45°,求旗杆AB的高度?
3.如图,身高 米的小明站在距路灯底部O点10米的点A处,他的身高 线段 在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
(1)在OQ上画出表示路灯灯泡位置的点P;
(2)小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;
(3)若 米,求路灯灯泡P到地面的距离.
知识点3 、正投影的概念
1.正投影:在平行投影中,投影线垂直于投影面产生的投影叫做正投影
2.正投影的规律
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:(1).线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
(2).平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
3.画几何体的正投影
物体正投影的形状、大小与它相对于投影面的位置有关
【新知导学】
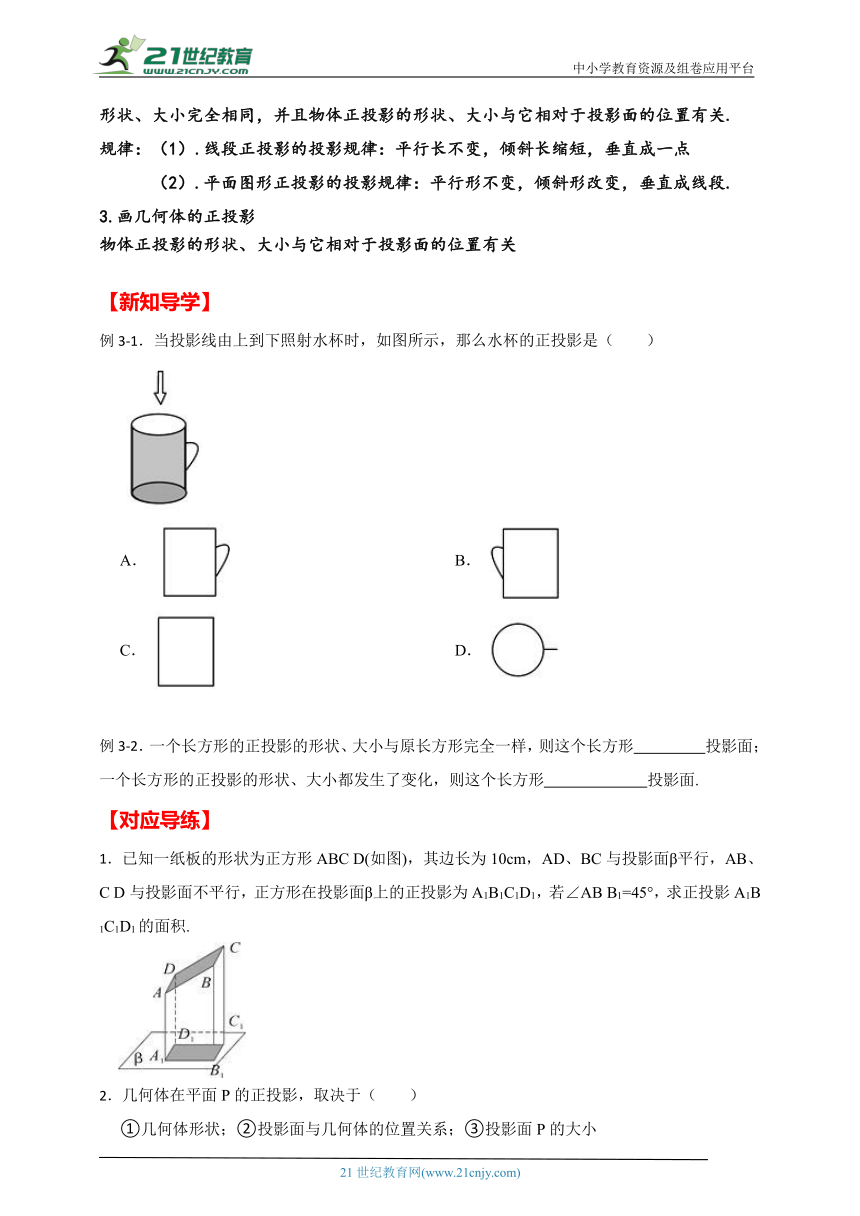
例3-1.当投影线由上到下照射水杯时,如图所示,那么水杯的正投影是( )
A. B.
C. D.
例3-2.一个长方形的正投影的形状、大小与原长方形完全一样,则这个长方形 投影面;一个长方形的正投影的形状、大小都发生了变化,则这个长方形 投影面.
【对应导练】
1.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1,若∠AB B1=45°,求正投影A1B 1C1D1的面积.
2.几何体在平面P的正投影,取决于( )
①几何体形状;②投影面与几何体的位置关系;③投影面P的大小
A.①② B.①③ C.②③ D.①②③
3.把一个正五棱柱如图摆放,当投射线由正前方射到后方时,它的正投影是( )
A. B. C. D.
题型训练
利用平行投影求物体高度
1.小王的身高是,在太阳光线下,他的影长是.
(1)小明的身高是,求同一时刻小明的影长(精确到).
(2)同一时刻旗杆的影长是,求旗杆的高.
2.据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,木杆长,它的影长为,测得为,求金字塔的高度.
3.如图所示,太阳光与地面成60°角,一颗倾斜的大树在地面上所成的角为30°,这时测得大树在地面上的影长约为10m,试求此大树的长约是多少?(得数保留整数)
利用中心投影与相似解决生活问题
4.如图分别是两根木棒及其影子的情形.
(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
5.如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?
6.高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
正投影与作图
7 .画出下列立体图形投影线从上方射向下方的正投影.
8 .画出如图摆放的正方体在投影面P上的正投影.
(1) 正方体的一个面ABCD平行于投影面P;
(2) 正方体的一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面P,并且其对角线AE垂直于投影面P.
【答案】见解析。
【解析】如图所示:
三、课堂达标
一、选择题(每小题4分,共32分)
1.晚上小亮在路灯下散步,在小亮从远处走到灯下,再远离路灯这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
2.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆 B.圆柱 C.梯形 D.矩形
3.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是( )
A.A B C D B.D B C A
C.C D A B D.A C B D
4.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
5.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
6.如图,灯光与影子的位置最合理的是( )
A. B.
C. D.
7.圆桌上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影,如图,已知桌面的直径1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A.0.36π平方米 B.0.81π平方米
C.2π平方米 D.3.24π平方米
8.春分时日,小彬上午9:00出去,测量了自己的影长,出去了一段时间之后,回来时,他发现这时的影长和上午出去时的影长一样长,则小彬出去的时间大约是( )小时.
A.2 B.4 C.6 D.8
二、填空题(每小题4分,共20分)
9.如图,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).
10.在数学活动课上,老师带领数学小组测量大树 的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离 为2m,那么这棵大树高 m.
11.如图,林林在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则该树的高度为
12.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为 m
13.如图:(A)(B)(C)(D)是一天中四个不同时刻的木杆在地面上的影子,将它们按时间先后顺序进行排列,为 .
三、解答题(每小题8分,共48分)
14.如图,AB表示一个窗户的高,AM和BN表示射人室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,求窗户的高度AB.
15.如图,树、红旗、人在同一直线上,已知人的影子为AB,树的影子为CD,确定光源的位置并画出旗杆的影子.
16.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
17.如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°.(以下计算结果都保留根号)
(1)求影子EB的长;
(2)若∠SAC=60°,求光源S离开地面的高度.
18.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的.请你确定此时路灯光源的位置.
19.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.1 投影
学习目标:
1、理解投影的有关概念,能根据光线的方向辨认物体的投影。
2、理解平行投影和中心投影的区别与联系。
3、理解正投影概念,理解现实生活中影子的现象,学会用数学知识尝试解答。
学习重点:理解平行投影、中心投影、正投影的特征。
学习难点:在投影面上画出平面图形的平行投影、中心投影、正投影。
老师告诉你
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:1.线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
2.平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
一、知识点拨
知识点1 、 平行投影
1.投影的概念:
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面
2.平行投影:由平行光线所形成的投影称为平行投影.
注意:平行投影中物体与投影面平行时的投影是全等的.
判断投影是平行投影的方法是看光线是否是平行的.如果光线是平行的,所得到的投影就是平行投影.
【新知导学】
例1-1.下面四幅图是某校园内一棵小树不同时刻在太阳光下的影子,按照时间的先后顺序排列,是 .
【答案】③④①②
【知识点】平行投影
【解析】【解答】解:根据平行投影的特点和规律可知,③,④是上午,①,②是下午,
根据影子的长度可知先后为③④①②.
故答案为:③④①②.
【分析】我们国家在北半球,从早晨到傍晚物体的影子的指向是:西、西北、北、东北、东,影长由长变短,再变长.
例1-2.在太阳光的照射下,摆动一张正方形卡片,它在地面上的投影可能是什么图形
【答案】解:在太阳光的照射下,摆动一张正方形卡片,它在地面上的投影可能正方形、长方形、菱形、平行四边形或一条直线.
【知识点】平行投影
【解析】【分析】利用平行投影的性质思考解题即可.
【对应导练】
1.如图,有甲、乙两根木杆,线段AB是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.
【答案】解:如图所示:
【知识点】平行投影;作图-平行线
【解析】【分析】已知线段AB是甲木杆的投影,连接甲杆的顶端与B即可得到太阳光线,再根据太阳光线互相平行,过乙的顶端做刚才得到太阳光线的平行线.
2.下列投影是平行投影的是( )
A.太阳光下窗户的影子 B.台灯下书本的影子
C.在手电筒照射下纸片的影子 D.路灯下行人的影子
【答案】A
【知识点】平行投影
【解析】【解答】A、太阳光下窗户的影子,是平行投影,故本选项正确;B、台灯下书本的影子是中心投影,故本选项错误;C、在手电筒照射下纸片的影子是中心投影,故本选项错误;D、路灯下行人的影子是中心投影,故本选项错误;故选A.
【分析】可根据平行投影的特点分析求解,或根据常识直接确定答案即可.
3.已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
(1)请你在图中画出此时DE在太阳光下的投影EF;
(2)在测量AB的投影时,同时测量出DE在太阳光下的投影EF长为6m,请你计算DE的长.
【答案】(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影,如图;
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴=,即=
∴DE=12(m).
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)根据太阳光线为平行光线,连结AC,然后过D点作AC的平行线交BC于E即可;
(2)证明△ABC∽△DEF,利用相似比计算DE的长.
4.在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼,大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为,已知此时高的竹竿在水平地面上的影子长,那么这棵大树高度是多少?
【答案】解:如图所示,过作于,
则,.
同一时刻物高和影长成正比,
,
,
,
答:这棵大树高为.
【知识点】平行投影
【解析】【分析】 过D作DE⊥AB于E, 在BE=CD=2m,DE=BC=5m,进而根据同一时刻物高和影长成正比建立方程,求解即可.
知识点2 、中心投影
1.中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.
2.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
3.判断投影是中心投影的方法是看光线是否相交于一点,如果光线是相交于一点,那么所得到的投影就是中心投影。
4.视点、视角和盲区
(1)把观察者所处的位置定为一点,叫视点.
(2)人眼到视平面的距离视固定的(视距),视平面左右两个边缘到人眼的连线得到的角度就是视角.
(3)盲区:视线到达不了的区域为盲区
【新知导学】
例2-1.下列现象属于中心投影的有( )
①小孔成像; ②皮影戏;③手影; ④放电影.
A.1个 B.2个 C.3个 D.4个
【答案】D
【知识点】中心投影
【解析】【解答】解:根据中心投影的定义可知答案为:D,
故答案为:D.
【分析】中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影。这个“点”就是中心,生活中能形成中心投影的点光源主要有手电筒、路灯、台灯、投影仪的灯光、放映机的灯光等。由此可得出答案.
例2-2.某公园一角有一盏地面射灯照在一棵树上,树的影子投在墙上.已知树高1m,树与墙之间的距离为10m,与射灯之间的距离为5m.求树在墙上的影长.
【答案】∵树高:影子长=灯与树距离:灯与墙的距离,
∴1:影子长=5:15,解得,影子长=3m.
【知识点】中心投影
【解析】【分析】根据中心投影的概念,列出比例式求解.
【对应导练】
1. 如图,路灯下一墙墩(用线段表示)的影子是,小明(用线段表示)的影子是,在M处有一棵大树,它在这个路灯下的影子是.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段.
【答案】(1)解:见解析:如图,点P即为所求,
(2)解:见解析:如图,线段即为所求.
【知识点】中心投影
【解析】【解答】解:
【分析】 (1)连接CA、FD并延长,交点即为路灯P的位置;
(2)连接PN,过点M作MQ⊥MN交PN于Q,MQ即为表示大树的线段.
2.如图所示,小红想利用竹竿来测量旗杆AB的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为4 米,∠DCE=45°,求旗杆AB的高度?
【答案】解:延长AD交BC的延长线于点F,过点D作DE⊥BC于点E,
∵CD 米,∠DCE=45°,
∴DE=CE=CD =4,
∵同一时刻物高与影长成正比,
∴ ,解得EF=2DE=8,
∴BF=10+4+8=22,
∵DE⊥BC,AB⊥BC,
∴△EDF∽△BAF,
∴ ,即 ,
∴AB=11米.
答:旗杆的高度为11米.
【知识点】相似三角形的应用;中心投影
【解析】【分析】 延长AD交BC的延长线于点F,过点D作DE⊥BC于点E, 证出 △EDF∽△BAF, 再利用相似三角形的性质列出比例式求解即可。
3.如图,身高 米的小明站在距路灯底部O点10米的点A处,他的身高 线段 在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
(1)在OQ上画出表示路灯灯泡位置的点P;
(2)小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;
(3)若 米,求路灯灯泡P到地面的距离.
【答案】(1)
(2)如图:
(3)∵AB∥OP,
∽ ,
,即 ,
解得 .
即路灯灯泡P到地面的距离是8米.
【知识点】相似三角形的判定与性质;中心投影
【解析】【分析】(1)根据中心投影的性质,连接MB并延长交OQ于一点,该点就是路灯灯泡位置的点P ;
(2)根据中心投影的性质,连接PD并延长,交OM于点N,线段CN就是小明在路灯下的影子;
(3)根据平行于三角形一边的直线,截其它两边,所截的三角形与原三角形相似得出 △MAB∽△MOP, ,根据相似三角形对应边成比例得出 , 根据比例式建立方程求解即可求出OP的长,从而得出答案。
知识点3 、正投影的概念
1.正投影:在平行投影中,投影线垂直于投影面产生的投影叫做正投影
2.正投影的规律
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:(1).线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
(2).平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
3.画几何体的正投影
物体正投影的形状、大小与它相对于投影面的位置有关
【新知导学】
例3-1.当投影线由上到下照射水杯时,如图所示,那么水杯的正投影是( )
A. B.
C. D.
【答案】D
【知识点】平行投影
【解析】【解答】解:投影线的方向是从上往下,因为杯口和杯底是圆,所以能看到一个圆和一条小线段。
故答案为:D。
【分析】由投影线的照射方向,可从向上往下看水杯得到图形。
例3-2.一个长方形的正投影的形状、大小与原长方形完全一样,则这个长方形 投影面;一个长方形的正投影的形状、大小都发生了变化,则这个长方形 投影面.
【答案】//;不平行于
【知识点】平行投影
【解析】【解答】解:长方形与投影面平行时,正投影不改变大小;
当长方形与投影面不平行时,正投影的形状将会改为,可能为线段,平行四边形。
故答案为://;不平行于
【分析】长方形的正投影与投影面的相对位置的不同,得到的正投影的大小也不一样。长方形与投影面的特殊的相对位置有:互相平行,互相垂直。平行时,正投影与原长方形形状大小一样;其他相对位置时,正投影的形状大小将会改变。
【对应导练】
1.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1,若∠AB B1=45°,求正投影A1B 1C1D1的面积.
【答案】解:过A作AE
BB1,交于点E,
因为∠ABB1=45°,
所以AE=BE=
cm
因为四边形ABCD是正方形,AD、BC与投影面β平行,
所以A1D1=B1C1=AD=BC=10cm,
所以正投影A1B 1C1D1的面积=10×
=
(cm2)
【知识点】平行投影
【解析】【分析】AD、BC与投影面β平行,则A1D1=B1C1=AD=BC,而且四边形ABCD是正方形,可得正投影A1B 1C1D1是正方形,求出A1B1的长即可(根据∠ABB1=45°可求得)。
2.几何体在平面P的正投影,取决于( )
①几何体形状;②投影面与几何体的位置关系;③投影面P的大小
A.①② B.①③ C.②③ D.①②③
【答案】A
【知识点】平行投影
【解析】【解答】解:∵几何体在平面的正投影与几何体的形状、投影面与几何体的位置有关,与投影面的大小无关,
∴只有①②符合题意
故答案为;A
【分析】根据几何体在平面的正投影与几何体的形状、投影面与几何体的位置有关,与投影面的大小无关,即可得出答案。
3.把一个正五棱柱如图摆放,当投射线由正前方射到后方时,它的正投影是( )
A. B. C. D.
【答案】B
【知识点】简单几何体的三视图;平行投影
【解析】【解答】根据投影的性质可得,该物体为五棱柱,则正投影应为矩形.故选B.
【分析】根据正投影的性质:当投射线由正前方射到后方时,其正投影应是矩形.
题型训练
利用平行投影求物体高度
1.小王的身高是,在太阳光线下,他的影长是.
(1)小明的身高是,求同一时刻小明的影长(精确到).
(2)同一时刻旗杆的影长是,求旗杆的高.
【答案】(1)解:设同一时刻小明的影长为xm,则
.
解得.
答:同一时刻小明的影长约为1.45m;
(2)解:设旗杆高为hm,则
.
解得.
答:旗杆的高为18.64m.
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)设同一时刻小明的影长为xm,同时同地物高与影长成正比,据此列式计算即可得解;
(2)设同一时刻旗杆高为hm,同时同地物高与影长成正比,据此列式计算即可得解.
2.据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,木杆长,它的影长为,测得为,求金字塔的高度.
【答案】解:太阳光线是平行线,.
又,,
,.
答:金字塔的高度为.
【知识点】相似三角形的应用;平行投影
【解析】【分析】由平行线的性质证出,根据对应边成比例求解即可.
3.如图所示,太阳光与地面成60°角,一颗倾斜的大树在地面上所成的角为30°,这时测得大树在地面上的影长约为10m,试求此大树的长约是多少?(得数保留整数)
【答案】解:过B作BM⊥AC于M,
∵∠A=30°,
∴BM= BC=5,AM=5 ,
又∵∠CBE=60°,
∴∠ACB=30°,
∴AB=CB,
∴CM=AM=5 ,
∴AC=10 ≈17.
答:此大树的长约是17m.
【知识点】三角形的外角性质;等腰三角形的判定与性质;含30°角的直角三角形;平行投影
【解析】【分析】先过B作BM⊥AC于M,构造含30°角的直角三角形,求得AM的长,再根据△ABC为等腰三角形,利用三线合一求得AC的长.
利用中心投影与相似解决生活问题
4.如图分别是两根木棒及其影子的情形.
(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
【答案】解:(1)图2反映了太阳光下的情形,图1反映了路灯下的情形;(2)设旗杆的高为xm,根据题意得,解得x=6,所以旗杆的高为6m;(3)如图1中,FG为在路灯下的第三根木棒的影长;如图2,FG为在太阳光下的第三根木棒的影长.
【知识点】平行投影;中心投影
【解析】【分析】(1)把木棒的顶端与投影的顶点连结起来即可得到投影线,然后根据投影线的关系判断是中心投影还是平行投影;
(2)对于平移投影,根据同一时刻身高与影长正比例进行计算;
(3)根据中心投影和平行投影的定义画图.
5.如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?
【答案】解:(1)因为球在灯光的正下方,所以阴影是圆形;(2)白炽灯向上移时,阴影会逐渐变小;(3)设球在地面上阴影的半径为x米,则,解得:x2=,则S阴影=π平方米.
【知识点】中心投影
【解析】【分析】(1)球在灯光的正下方,所以阴影是圆形;
(2)根据中心投影的特点可知:在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以白炽灯向上移时,阴影会逐渐变小;
(3)先根据相似求出阴影的半径,再求面积.
6.高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
【答案】解:(1)
(2)由于BF=DB=2(米),即∠D=45°,
所以,DP=OP=灯高,
△COP中AE⊥CP,OP⊥CP,
∴AE∥OP
∴△CEA∽△COP,即,
设AP=x,OP=h则:
①,
DP=OP表达为2+4+x=h②,
联立①②两式得:
x=4,h=10,
∴路灯有10米高.
【知识点】中心投影
【解析】【分析】(1)连接DF并延长与CE的延长线交与一点即可得到路灯的位置;
(2)由于BF=DB=2米,即∠D=45°,则DP=OP=灯高,得出△CEA∽△COP,即,进而求出路灯的高.
正投影与作图
7 .画出下列立体图形投影线从上方射向下方的正投影.
【答案】见解析。
【解析】如图所示:
8 .画出如图摆放的正方体在投影面P上的正投影.
(1) 正方体的一个面ABCD平行于投影面P;
(2) 正方体的一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面P,并且其对角线AE垂直于投影面P.
【答案】见解析。
【解析】如图所示:
三、课堂达标
一、选择题(每小题4分,共32分)
1.晚上小亮在路灯下散步,在小亮从远处走到灯下,再远离路灯这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
【答案】B
【知识点】中心投影
【解析】【解答】解:晚上小亮在路灯下散步,当小亮从远处走到灯下的时候,他在地上的影子由长变短,当他再远离路灯的时候,他在地上的影子由短变长.
故选B.
【分析】根据中心投影的定义当小亮从远处走到灯下,他在地上的影子逐渐变短,当他再远离路灯的时,他在地上的影子逐渐变长.
2.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆 B.圆柱 C.梯形 D.矩形
【答案】D
【知识点】平行投影
【解析】【解答】解:根据平行投影特点,图中圆柱体的正投影是矩形.故选D.
【分析】根据平行投影特点可知.
3.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是( )
A.A B C D B.D B C A
C.C D A B D.A C B D
【答案】C
【知识点】平行投影
【解析】【解答】解:根据平行投影的特点和规律可知,C,D是上午,A,B是下午,
根据影子的长度可知先后为C→D→A→B.
故选C.
【分析】解:根据平行投影的特点和规律可知,C,D是上午,A,B是下午,根据影子的长度可知先后为C→D→A→B.
4.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
【答案】C
【知识点】中心投影
【解析】【解答】解:根据两个人的影子在两个相反的方向,则一定是中心投影;且两人同在光源两侧.故答案为:C.
【分析】由平行投影中影子的长度取决于物体的长度,中心投影中影子的长度和方向不仅与物体的长度有关,而且还要看物体到光源的距离可以得出本题结论.
5.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
【答案】A
【知识点】中心投影
【解析】【解答】根据光源是由远到近的过程和中心投影的特点可得:小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短,
故答案为:A.
【分析】该投影是中心投影, 小亮从A处向着路灯灯柱方向径直走到B处 的过程中,光源是由远到近的过程,根据中心投影的特点,小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短。
6.如图,灯光与影子的位置最合理的是( )
A. B.
C. D.
【答案】B
【知识点】中心投影
【解析】【解答】解:根据中心投影的特点:①影子与光源应在物体的异侧,②连接物体和它影子的顶端的直线必定经过点光源;
故答案为:B.
【分析】根据中心投影特点一一分析即可得出答案.
7.圆桌上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影,如图,已知桌面的直径1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A.0.36π平方米 B.0.81π平方米
C.2π平方米 D.3.24π平方米
【答案】B
【知识点】相似三角形的性质;中心投影
【解析】【解答】如图,根据常识桌面与地面平行,
所以,△ADE∽△ABC,
∴
即 ,
解得BC=1.8,
所以,地面上阴影部分的面积= =0.81π(平方米).
故答案为:B.
【分析】根据常识,桌面与地面是平行的,然后判断出△ADE∽△ABC,根据相似三角形对应高的比等于对应边的比列出比例式,然后求出地面阴影部分的直径,再根据圆的面积公式列式进行计算即可得解.
8.春分时日,小彬上午9:00出去,测量了自己的影长,出去了一段时间之后,回来时,他发现这时的影长和上午出去时的影长一样长,则小彬出去的时间大约是( )小时.
A.2 B.4 C.6 D.8
【答案】C
【知识点】平行投影
【解析】【解答】解:依题意,要令影长相等,就要使太阳高度角相等.已知上午9:00与15:00的太阳高度角是相等的,
故可求出小彬出去的之间为15﹣9=6(小时).
故选:C.
【分析】结合题意,要使两个时间的影长相等,必须使阳光照射的角度相等,根据地理常识可知:上午9:00与15:00的阳光照射的角度相等,故则小彬出去的时间大约为6小时.
二、填空题(每小题4分,共20分)
9.如图,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).
【答案】变小
【知识点】中心投影
【解析】【解答】解:易知投影为光线路程从蜡烛A点到人物头所连接的直线延伸到墙上,设为AD.
当人离墙的距离变小时候(即往右边移动),易知其AD与AB的夹角会变小,AD长度变小,根据勾股定理易知,斜边变小,其中一条直角边固定不变,则另一条直角边肯定会长度变小.
故答案为:变小.
【分析】可连接光源和人的头顶可知,墙上的影长和人到墙的距离变化规律是:距离墙越近,影长越短,距离墙越远影长越长.
10.在数学活动课上,老师带领数学小组测量大树 的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离 为2m,那么这棵大树高 m.
【答案】9
【知识点】平行投影
【解析】【解答】解:延长AD交BC延长线于E,
根据同一时刻影长与物高成比例可得CE:CD=1:1.4,
∵CD=2m,
∴CE= m,
∴BE=BC+CE=5+ = m,
∴BE:AB=1:1.4,
∴AB=9m.
故答案为:9.
【分析】根据同一时刻影长与物高成比例,先求出CE,再求AB即可.
11.如图,林林在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则该树的高度为
【答案】4m
【知识点】锐角三角函数的定义;平行投影
【解析】【解答】解:根据题意构建如图所示的三角形:
∴∠ECF=90°,ED=2 m,DF=8 m,CD为树高.
∵∠1+∠2=∠E+∠2=90°,
∴∠1=∠E.
∴tan E=tan∠ 1,
即 = ,
解得CD=4 m.
【分析】根据题意构建如图所示的三角形:根据同角的余角相等,再由等角的正切相等得 ,解之即可得出答案.
12.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为 m
【答案】5
【知识点】平行投影
【解析】【解答】解:小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
∵=,
∴=,解得GH=8,
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=GH=4,
在Rt△OGM中,OM=R﹣2,OG=R,GM=4,
∵OM2+GM2=OG2,
∴(R﹣2)2+42=R2,解得R=5,
即⊙O的半径为5m.
故答案为5m.
【分析】小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,先利用平行投影的性质和相似的性质得到=,于是可求出GH=8,再根据垂径定理得到点O在直线MN上,GM=HM=GH=4,然后根据勾股定理得到(R﹣2)2+42=R2,再解方程即可.
13.如图:(A)(B)(C)(D)是一天中四个不同时刻的木杆在地面上的影子,将它们按时间先后顺序进行排列,为 .
【答案】(D)(C)(A)(B)
【知识点】平行投影
【解析】【解答】解:太阳从东方升起最后从西面落下,木杆的影子应该在西面,随着时间的变化影子逐渐的向北偏西,南偏西,正东方向的顺序移动,故它们按时间先后顺序进行排列,为(D)(C)(A)(B).
【分析】根据影子变化的方向正好太阳所处的方向是相反的来判断.太阳从东方升起最后从西面落下确定影子的起始方向.
三、解答题(每小题8分,共48分)
14.如图,AB表示一个窗户的高,AM和BN表示射人室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,求窗户的高度AB.
【答案】解:∵BN∥AM,
∴∠CBN=∠A,∠CNB=∠M,
∴△CBN∽△CAM,
∴ 即
解得:CA=3,
∴AB=3-1=2,
答:窗户的高度AB为2m.
【知识点】相似三角形的性质;平行投影
【解析】【分析】阳光可看作一束平行光,由光的直线传播特性可知透过窗户后的光线BN与AE仍然平行,由此可得出一对相似三角形,由相似三角形的性质可求出AC的长,进而求出AB的长即窗户的高度.
15.如图,树、红旗、人在同一直线上,已知人的影子为AB,树的影子为CD,确定光源的位置并画出旗杆的影子.
【答案】解:如图所示是灯光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线,再过人的顶端及其影子的顶端作一条直线,两直线相交,其交点就是光源的位置;然后再过旗杆的顶端连接光源的直线,交地面于一点,连接这点与旗杆底端的线段就是旗杆的影子.
【知识点】平行投影
【解析】【分析】利用两个物体与影长的对应顶点的连线交于一点,这样得到的投影是中心投影,此点就是光源的位置所在.
16.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
【答案】解:(1)如图所示:P点即为路灯的位置;
(2)如图所示:GM即为所求.
【知识点】中心投影
【解析】【分析】(1)利用对应点连线相交于一点进而得出路灯位置;
(2)利用路灯的位置得出大树高.
17.如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°.(以下计算结果都保留根号)
(1)求影子EB的长;
(2)若∠SAC=60°,求光源S离开地面的高度.
【答案】解:(1)∵圆锥的底面半径和高都为2m,∴CH=HE=2m,∵∠SBA=30°,∴HB=2m,∴影长BE=BH﹣HE=2﹣2(m);(2)作CD⊥SA于点D,在Rt△ACD中,得CD=ACcos30°=AC=,∵∠SBA=30°,∠SAB=∠SAC+∠BAC=60°+45°=105°,∴∠DSC=45°,∴SC==2,∴SB=2+BC=2+4,∴SF=SB=(+2)m,答:光源S离开地面的高度为(2+)m.
【知识点】中心投影
【解析】【分析】(1)根据已知得出CH=HE=2m,进而得出HB的长,即可得出BE的长;
(2)首先求出CD的长进而得出∠DSC=45°,利用锐角三角函数关系得出SC的长即可.
18.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的.请你确定此时路灯光源的位置.
【答案】解:
∴点O为路灯光源的位置.
【知识点】中心投影
【解析】【分析】直接连接树的顶端和影子的顶端形成的直线,再根据反射的原理作出经过玻璃反射的光线形成的直线,两条直线的交点处即为点光源的位置.
19.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
【答案】解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴,即,解得DE=10(m),
即DE的长为10m.
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)连结AC,过点D作DF∥AC,则EF为所求;
(2)先证明Rt△ABC∽Rt△DEF,然后利用相似比计算出DE的长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.1 投影
学习目标:
1、理解投影的有关概念,能根据光线的方向辨认物体的投影。
2、理解平行投影和中心投影的区别与联系。
3、理解正投影概念,理解现实生活中影子的现象,学会用数学知识尝试解答。
学习重点:理解平行投影、中心投影、正投影的特征。
学习难点:在投影面上画出平面图形的平行投影、中心投影、正投影。
老师告诉你
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:1.线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
2.平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
一、知识点拨
知识点1 、 平行投影
1.投影的概念:
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面
2.平行投影:由平行光线所形成的投影称为平行投影.
注意:平行投影中物体与投影面平行时的投影是全等的.
判断投影是平行投影的方法是看光线是否是平行的.如果光线是平行的,所得到的投影就是平行投影.
【新知导学】
例1-1.下面四幅图是某校园内一棵小树不同时刻在太阳光下的影子,按照时间的先后顺序排列,是 .
例1-2.在太阳光的照射下,摆动一张正方形卡片,它在地面上的投影可能是什么图形
【对应导练】
1.如图,有甲、乙两根木杆,线段AB是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.
2.下列投影是平行投影的是( )
A.太阳光下窗户的影子 B.台灯下书本的影子
C.在手电筒照射下纸片的影子 D.路灯下行人的影子
3.已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
(1)请你在图中画出此时DE在太阳光下的投影EF;
(2)在测量AB的投影时,同时测量出DE在太阳光下的投影EF长为6m,请你计算DE的长.
4.在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼,大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为,已知此时高的竹竿在水平地面上的影子长,那么这棵大树高度是多少?
知识点2 、中心投影
1.中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.
2.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
3.判断投影是中心投影的方法是看光线是否相交于一点,如果光线是相交于一点,那么所得到的投影就是中心投影。
4.视点、视角和盲区
(1)把观察者所处的位置定为一点,叫视点.
(2)人眼到视平面的距离视固定的(视距),视平面左右两个边缘到人眼的连线得到的角度就是视角.
(3)盲区:视线到达不了的区域为盲区
【新知导学】
例2-1.下列现象属于中心投影的有( )
①小孔成像; ②皮影戏;③手影; ④放电影.
A.1个 B.2个 C.3个 D.4个
例2-2.某公园一角有一盏地面射灯照在一棵树上,树的影子投在墙上.已知树高1m,树与墙之间的距离为10m,与射灯之间的距离为5m.求树在墙上的影长.
【对应导练】
1. 如图,路灯下一墙墩(用线段表示)的影子是,小明(用线段表示)的影子是,在M处有一棵大树,它在这个路灯下的影子是.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段.
2.如图所示,小红想利用竹竿来测量旗杆AB的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为4 米,∠DCE=45°,求旗杆AB的高度?
3.如图,身高 米的小明站在距路灯底部O点10米的点A处,他的身高 线段 在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
(1)在OQ上画出表示路灯灯泡位置的点P;
(2)小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;
(3)若 米,求路灯灯泡P到地面的距离.
知识点3 、正投影的概念
1.正投影:在平行投影中,投影线垂直于投影面产生的投影叫做正投影
2.正投影的规律
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:(1).线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
(2).平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
3.画几何体的正投影
物体正投影的形状、大小与它相对于投影面的位置有关
【新知导学】
例3-1.当投影线由上到下照射水杯时,如图所示,那么水杯的正投影是( )
A. B.
C. D.
例3-2.一个长方形的正投影的形状、大小与原长方形完全一样,则这个长方形 投影面;一个长方形的正投影的形状、大小都发生了变化,则这个长方形 投影面.
【对应导练】
1.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1,若∠AB B1=45°,求正投影A1B 1C1D1的面积.
2.几何体在平面P的正投影,取决于( )
①几何体形状;②投影面与几何体的位置关系;③投影面P的大小
A.①② B.①③ C.②③ D.①②③
3.把一个正五棱柱如图摆放,当投射线由正前方射到后方时,它的正投影是( )
A. B. C. D.
题型训练
利用平行投影求物体高度
1.小王的身高是,在太阳光线下,他的影长是.
(1)小明的身高是,求同一时刻小明的影长(精确到).
(2)同一时刻旗杆的影长是,求旗杆的高.
2.据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,木杆长,它的影长为,测得为,求金字塔的高度.
3.如图所示,太阳光与地面成60°角,一颗倾斜的大树在地面上所成的角为30°,这时测得大树在地面上的影长约为10m,试求此大树的长约是多少?(得数保留整数)
利用中心投影与相似解决生活问题
4.如图分别是两根木棒及其影子的情形.
(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
5.如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?
6.高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
正投影与作图
7 .画出下列立体图形投影线从上方射向下方的正投影.
8 .画出如图摆放的正方体在投影面P上的正投影.
(1) 正方体的一个面ABCD平行于投影面P;
(2) 正方体的一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面P,并且其对角线AE垂直于投影面P.
【答案】见解析。
【解析】如图所示:
三、课堂达标
一、选择题(每小题4分,共32分)
1.晚上小亮在路灯下散步,在小亮从远处走到灯下,再远离路灯这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
2.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆 B.圆柱 C.梯形 D.矩形
3.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是( )
A.A B C D B.D B C A
C.C D A B D.A C B D
4.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
5.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
6.如图,灯光与影子的位置最合理的是( )
A. B.
C. D.
7.圆桌上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影,如图,已知桌面的直径1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A.0.36π平方米 B.0.81π平方米
C.2π平方米 D.3.24π平方米
8.春分时日,小彬上午9:00出去,测量了自己的影长,出去了一段时间之后,回来时,他发现这时的影长和上午出去时的影长一样长,则小彬出去的时间大约是( )小时.
A.2 B.4 C.6 D.8
二、填空题(每小题4分,共20分)
9.如图,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).
10.在数学活动课上,老师带领数学小组测量大树 的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离 为2m,那么这棵大树高 m.
11.如图,林林在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则该树的高度为
12.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为 m
13.如图:(A)(B)(C)(D)是一天中四个不同时刻的木杆在地面上的影子,将它们按时间先后顺序进行排列,为 .
三、解答题(每小题8分,共48分)
14.如图,AB表示一个窗户的高,AM和BN表示射人室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,求窗户的高度AB.
15.如图,树、红旗、人在同一直线上,已知人的影子为AB,树的影子为CD,确定光源的位置并画出旗杆的影子.
16.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
17.如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°.(以下计算结果都保留根号)
(1)求影子EB的长;
(2)若∠SAC=60°,求光源S离开地面的高度.
18.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的.请你确定此时路灯光源的位置.
19.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.1 投影
学习目标:
1、理解投影的有关概念,能根据光线的方向辨认物体的投影。
2、理解平行投影和中心投影的区别与联系。
3、理解正投影概念,理解现实生活中影子的现象,学会用数学知识尝试解答。
学习重点:理解平行投影、中心投影、正投影的特征。
学习难点:在投影面上画出平面图形的平行投影、中心投影、正投影。
老师告诉你
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:1.线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
2.平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
一、知识点拨
知识点1 、 平行投影
1.投影的概念:
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面
2.平行投影:由平行光线所形成的投影称为平行投影.
注意:平行投影中物体与投影面平行时的投影是全等的.
判断投影是平行投影的方法是看光线是否是平行的.如果光线是平行的,所得到的投影就是平行投影.
【新知导学】
例1-1.下面四幅图是某校园内一棵小树不同时刻在太阳光下的影子,按照时间的先后顺序排列,是 .
【答案】③④①②
【知识点】平行投影
【解析】【解答】解:根据平行投影的特点和规律可知,③,④是上午,①,②是下午,
根据影子的长度可知先后为③④①②.
故答案为:③④①②.
【分析】我们国家在北半球,从早晨到傍晚物体的影子的指向是:西、西北、北、东北、东,影长由长变短,再变长.
例1-2.在太阳光的照射下,摆动一张正方形卡片,它在地面上的投影可能是什么图形
【答案】解:在太阳光的照射下,摆动一张正方形卡片,它在地面上的投影可能正方形、长方形、菱形、平行四边形或一条直线.
【知识点】平行投影
【解析】【分析】利用平行投影的性质思考解题即可.
【对应导练】
1.如图,有甲、乙两根木杆,线段AB是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.
【答案】解:如图所示:
【知识点】平行投影;作图-平行线
【解析】【分析】已知线段AB是甲木杆的投影,连接甲杆的顶端与B即可得到太阳光线,再根据太阳光线互相平行,过乙的顶端做刚才得到太阳光线的平行线.
2.下列投影是平行投影的是( )
A.太阳光下窗户的影子 B.台灯下书本的影子
C.在手电筒照射下纸片的影子 D.路灯下行人的影子
【答案】A
【知识点】平行投影
【解析】【解答】A、太阳光下窗户的影子,是平行投影,故本选项正确;B、台灯下书本的影子是中心投影,故本选项错误;C、在手电筒照射下纸片的影子是中心投影,故本选项错误;D、路灯下行人的影子是中心投影,故本选项错误;故选A.
【分析】可根据平行投影的特点分析求解,或根据常识直接确定答案即可.
3.已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
(1)请你在图中画出此时DE在太阳光下的投影EF;
(2)在测量AB的投影时,同时测量出DE在太阳光下的投影EF长为6m,请你计算DE的长.
【答案】(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影,如图;
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴=,即=
∴DE=12(m).
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)根据太阳光线为平行光线,连结AC,然后过D点作AC的平行线交BC于E即可;
(2)证明△ABC∽△DEF,利用相似比计算DE的长.
4.在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼,大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为,已知此时高的竹竿在水平地面上的影子长,那么这棵大树高度是多少?
【答案】解:如图所示,过作于,
则,.
同一时刻物高和影长成正比,
,
,
,
答:这棵大树高为.
【知识点】平行投影
【解析】【分析】 过D作DE⊥AB于E, 在BE=CD=2m,DE=BC=5m,进而根据同一时刻物高和影长成正比建立方程,求解即可.
知识点2 、中心投影
1.中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.
2.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
3.判断投影是中心投影的方法是看光线是否相交于一点,如果光线是相交于一点,那么所得到的投影就是中心投影。
4.视点、视角和盲区
(1)把观察者所处的位置定为一点,叫视点.
(2)人眼到视平面的距离视固定的(视距),视平面左右两个边缘到人眼的连线得到的角度就是视角.
(3)盲区:视线到达不了的区域为盲区
【新知导学】
例2-1.下列现象属于中心投影的有( )
①小孔成像; ②皮影戏;③手影; ④放电影.
A.1个 B.2个 C.3个 D.4个
【答案】D
【知识点】中心投影
【解析】【解答】解:根据中心投影的定义可知答案为:D,
故答案为:D.
【分析】中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影。这个“点”就是中心,生活中能形成中心投影的点光源主要有手电筒、路灯、台灯、投影仪的灯光、放映机的灯光等。由此可得出答案.
例2-2.某公园一角有一盏地面射灯照在一棵树上,树的影子投在墙上.已知树高1m,树与墙之间的距离为10m,与射灯之间的距离为5m.求树在墙上的影长.
【答案】∵树高:影子长=灯与树距离:灯与墙的距离,
∴1:影子长=5:15,解得,影子长=3m.
【知识点】中心投影
【解析】【分析】根据中心投影的概念,列出比例式求解.
【对应导练】
1. 如图,路灯下一墙墩(用线段表示)的影子是,小明(用线段表示)的影子是,在M处有一棵大树,它在这个路灯下的影子是.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段.
【答案】(1)解:见解析:如图,点P即为所求,
(2)解:见解析:如图,线段即为所求.
【知识点】中心投影
【解析】【解答】解:
【分析】 (1)连接CA、FD并延长,交点即为路灯P的位置;
(2)连接PN,过点M作MQ⊥MN交PN于Q,MQ即为表示大树的线段.
2.如图所示,小红想利用竹竿来测量旗杆AB的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为4 米,∠DCE=45°,求旗杆AB的高度?
【答案】解:延长AD交BC的延长线于点F,过点D作DE⊥BC于点E,
∵CD 米,∠DCE=45°,
∴DE=CE=CD =4,
∵同一时刻物高与影长成正比,
∴ ,解得EF=2DE=8,
∴BF=10+4+8=22,
∵DE⊥BC,AB⊥BC,
∴△EDF∽△BAF,
∴ ,即 ,
∴AB=11米.
答:旗杆的高度为11米.
【知识点】相似三角形的应用;中心投影
【解析】【分析】 延长AD交BC的延长线于点F,过点D作DE⊥BC于点E, 证出 △EDF∽△BAF, 再利用相似三角形的性质列出比例式求解即可。
3.如图,身高 米的小明站在距路灯底部O点10米的点A处,他的身高 线段 在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
(1)在OQ上画出表示路灯灯泡位置的点P;
(2)小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;
(3)若 米,求路灯灯泡P到地面的距离.
【答案】(1)
(2)如图:
(3)∵AB∥OP,
∽ ,
,即 ,
解得 .
即路灯灯泡P到地面的距离是8米.
【知识点】相似三角形的判定与性质;中心投影
【解析】【分析】(1)根据中心投影的性质,连接MB并延长交OQ于一点,该点就是路灯灯泡位置的点P ;
(2)根据中心投影的性质,连接PD并延长,交OM于点N,线段CN就是小明在路灯下的影子;
(3)根据平行于三角形一边的直线,截其它两边,所截的三角形与原三角形相似得出 △MAB∽△MOP, ,根据相似三角形对应边成比例得出 , 根据比例式建立方程求解即可求出OP的长,从而得出答案。
知识点3 、正投影的概念
1.正投影:在平行投影中,投影线垂直于投影面产生的投影叫做正投影
2.正投影的规律
物体正投影的投影规律:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
规律:(1).线段正投影的投影规律:平行长不变,倾斜长缩短,垂直成一点
(2).平面图形正投影的投影规律:平行形不变,倾斜形改变,垂直成线段.
3.画几何体的正投影
物体正投影的形状、大小与它相对于投影面的位置有关
【新知导学】
例3-1.当投影线由上到下照射水杯时,如图所示,那么水杯的正投影是( )
A. B.
C. D.
【答案】D
【知识点】平行投影
【解析】【解答】解:投影线的方向是从上往下,因为杯口和杯底是圆,所以能看到一个圆和一条小线段。
故答案为:D。
【分析】由投影线的照射方向,可从向上往下看水杯得到图形。
例3-2.一个长方形的正投影的形状、大小与原长方形完全一样,则这个长方形 投影面;一个长方形的正投影的形状、大小都发生了变化,则这个长方形 投影面.
【答案】//;不平行于
【知识点】平行投影
【解析】【解答】解:长方形与投影面平行时,正投影不改变大小;
当长方形与投影面不平行时,正投影的形状将会改为,可能为线段,平行四边形。
故答案为://;不平行于
【分析】长方形的正投影与投影面的相对位置的不同,得到的正投影的大小也不一样。长方形与投影面的特殊的相对位置有:互相平行,互相垂直。平行时,正投影与原长方形形状大小一样;其他相对位置时,正投影的形状大小将会改变。
【对应导练】
1.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1,若∠AB B1=45°,求正投影A1B 1C1D1的面积.
【答案】解:过A作AE
BB1,交于点E,
因为∠ABB1=45°,
所以AE=BE=
cm
因为四边形ABCD是正方形,AD、BC与投影面β平行,
所以A1D1=B1C1=AD=BC=10cm,
所以正投影A1B 1C1D1的面积=10×
=
(cm2)
【知识点】平行投影
【解析】【分析】AD、BC与投影面β平行,则A1D1=B1C1=AD=BC,而且四边形ABCD是正方形,可得正投影A1B 1C1D1是正方形,求出A1B1的长即可(根据∠ABB1=45°可求得)。
2.几何体在平面P的正投影,取决于( )
①几何体形状;②投影面与几何体的位置关系;③投影面P的大小
A.①② B.①③ C.②③ D.①②③
【答案】A
【知识点】平行投影
【解析】【解答】解:∵几何体在平面的正投影与几何体的形状、投影面与几何体的位置有关,与投影面的大小无关,
∴只有①②符合题意
故答案为;A
【分析】根据几何体在平面的正投影与几何体的形状、投影面与几何体的位置有关,与投影面的大小无关,即可得出答案。
3.把一个正五棱柱如图摆放,当投射线由正前方射到后方时,它的正投影是( )
A. B. C. D.
【答案】B
【知识点】简单几何体的三视图;平行投影
【解析】【解答】根据投影的性质可得,该物体为五棱柱,则正投影应为矩形.故选B.
【分析】根据正投影的性质:当投射线由正前方射到后方时,其正投影应是矩形.
题型训练
利用平行投影求物体高度
1.小王的身高是,在太阳光线下,他的影长是.
(1)小明的身高是,求同一时刻小明的影长(精确到).
(2)同一时刻旗杆的影长是,求旗杆的高.
【答案】(1)解:设同一时刻小明的影长为xm,则
.
解得.
答:同一时刻小明的影长约为1.45m;
(2)解:设旗杆高为hm,则
.
解得.
答:旗杆的高为18.64m.
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)设同一时刻小明的影长为xm,同时同地物高与影长成正比,据此列式计算即可得解;
(2)设同一时刻旗杆高为hm,同时同地物高与影长成正比,据此列式计算即可得解.
2.据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,木杆长,它的影长为,测得为,求金字塔的高度.
【答案】解:太阳光线是平行线,.
又,,
,.
答:金字塔的高度为.
【知识点】相似三角形的应用;平行投影
【解析】【分析】由平行线的性质证出,根据对应边成比例求解即可.
3.如图所示,太阳光与地面成60°角,一颗倾斜的大树在地面上所成的角为30°,这时测得大树在地面上的影长约为10m,试求此大树的长约是多少?(得数保留整数)
【答案】解:过B作BM⊥AC于M,
∵∠A=30°,
∴BM= BC=5,AM=5 ,
又∵∠CBE=60°,
∴∠ACB=30°,
∴AB=CB,
∴CM=AM=5 ,
∴AC=10 ≈17.
答:此大树的长约是17m.
【知识点】三角形的外角性质;等腰三角形的判定与性质;含30°角的直角三角形;平行投影
【解析】【分析】先过B作BM⊥AC于M,构造含30°角的直角三角形,求得AM的长,再根据△ABC为等腰三角形,利用三线合一求得AC的长.
利用中心投影与相似解决生活问题
4.如图分别是两根木棒及其影子的情形.
(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
【答案】解:(1)图2反映了太阳光下的情形,图1反映了路灯下的情形;(2)设旗杆的高为xm,根据题意得,解得x=6,所以旗杆的高为6m;(3)如图1中,FG为在路灯下的第三根木棒的影长;如图2,FG为在太阳光下的第三根木棒的影长.
【知识点】平行投影;中心投影
【解析】【分析】(1)把木棒的顶端与投影的顶点连结起来即可得到投影线,然后根据投影线的关系判断是中心投影还是平行投影;
(2)对于平移投影,根据同一时刻身高与影长正比例进行计算;
(3)根据中心投影和平行投影的定义画图.
5.如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?
【答案】解:(1)因为球在灯光的正下方,所以阴影是圆形;(2)白炽灯向上移时,阴影会逐渐变小;(3)设球在地面上阴影的半径为x米,则,解得:x2=,则S阴影=π平方米.
【知识点】中心投影
【解析】【分析】(1)球在灯光的正下方,所以阴影是圆形;
(2)根据中心投影的特点可知:在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以白炽灯向上移时,阴影会逐渐变小;
(3)先根据相似求出阴影的半径,再求面积.
6.高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
【答案】解:(1)
(2)由于BF=DB=2(米),即∠D=45°,
所以,DP=OP=灯高,
△COP中AE⊥CP,OP⊥CP,
∴AE∥OP
∴△CEA∽△COP,即,
设AP=x,OP=h则:
①,
DP=OP表达为2+4+x=h②,
联立①②两式得:
x=4,h=10,
∴路灯有10米高.
【知识点】中心投影
【解析】【分析】(1)连接DF并延长与CE的延长线交与一点即可得到路灯的位置;
(2)由于BF=DB=2米,即∠D=45°,则DP=OP=灯高,得出△CEA∽△COP,即,进而求出路灯的高.
正投影与作图
7 .画出下列立体图形投影线从上方射向下方的正投影.
【答案】见解析。
【解析】如图所示:
8 .画出如图摆放的正方体在投影面P上的正投影.
(1) 正方体的一个面ABCD平行于投影面P;
(2) 正方体的一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面P,并且其对角线AE垂直于投影面P.
【答案】见解析。
【解析】如图所示:
三、课堂达标
一、选择题(每小题4分,共32分)
1.晚上小亮在路灯下散步,在小亮从远处走到灯下,再远离路灯这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
【答案】B
【知识点】中心投影
【解析】【解答】解:晚上小亮在路灯下散步,当小亮从远处走到灯下的时候,他在地上的影子由长变短,当他再远离路灯的时候,他在地上的影子由短变长.
故选B.
【分析】根据中心投影的定义当小亮从远处走到灯下,他在地上的影子逐渐变短,当他再远离路灯的时,他在地上的影子逐渐变长.
2.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆 B.圆柱 C.梯形 D.矩形
【答案】D
【知识点】平行投影
【解析】【解答】解:根据平行投影特点,图中圆柱体的正投影是矩形.故选D.
【分析】根据平行投影特点可知.
3.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是( )
A.A B C D B.D B C A
C.C D A B D.A C B D
【答案】C
【知识点】平行投影
【解析】【解答】解:根据平行投影的特点和规律可知,C,D是上午,A,B是下午,
根据影子的长度可知先后为C→D→A→B.
故选C.
【分析】解:根据平行投影的特点和规律可知,C,D是上午,A,B是下午,根据影子的长度可知先后为C→D→A→B.
4.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
【答案】C
【知识点】中心投影
【解析】【解答】解:根据两个人的影子在两个相反的方向,则一定是中心投影;且两人同在光源两侧.故答案为:C.
【分析】由平行投影中影子的长度取决于物体的长度,中心投影中影子的长度和方向不仅与物体的长度有关,而且还要看物体到光源的距离可以得出本题结论.
5.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
【答案】A
【知识点】中心投影
【解析】【解答】根据光源是由远到近的过程和中心投影的特点可得:小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短,
故答案为:A.
【分析】该投影是中心投影, 小亮从A处向着路灯灯柱方向径直走到B处 的过程中,光源是由远到近的过程,根据中心投影的特点,小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短。
6.如图,灯光与影子的位置最合理的是( )
A. B.
C. D.
【答案】B
【知识点】中心投影
【解析】【解答】解:根据中心投影的特点:①影子与光源应在物体的异侧,②连接物体和它影子的顶端的直线必定经过点光源;
故答案为:B.
【分析】根据中心投影特点一一分析即可得出答案.
7.圆桌上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影,如图,已知桌面的直径1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A.0.36π平方米 B.0.81π平方米
C.2π平方米 D.3.24π平方米
【答案】B
【知识点】相似三角形的性质;中心投影
【解析】【解答】如图,根据常识桌面与地面平行,
所以,△ADE∽△ABC,
∴
即 ,
解得BC=1.8,
所以,地面上阴影部分的面积= =0.81π(平方米).
故答案为:B.
【分析】根据常识,桌面与地面是平行的,然后判断出△ADE∽△ABC,根据相似三角形对应高的比等于对应边的比列出比例式,然后求出地面阴影部分的直径,再根据圆的面积公式列式进行计算即可得解.
8.春分时日,小彬上午9:00出去,测量了自己的影长,出去了一段时间之后,回来时,他发现这时的影长和上午出去时的影长一样长,则小彬出去的时间大约是( )小时.
A.2 B.4 C.6 D.8
【答案】C
【知识点】平行投影
【解析】【解答】解:依题意,要令影长相等,就要使太阳高度角相等.已知上午9:00与15:00的太阳高度角是相等的,
故可求出小彬出去的之间为15﹣9=6(小时).
故选:C.
【分析】结合题意,要使两个时间的影长相等,必须使阳光照射的角度相等,根据地理常识可知:上午9:00与15:00的阳光照射的角度相等,故则小彬出去的时间大约为6小时.
二、填空题(每小题4分,共20分)
9.如图,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).
【答案】变小
【知识点】中心投影
【解析】【解答】解:易知投影为光线路程从蜡烛A点到人物头所连接的直线延伸到墙上,设为AD.
当人离墙的距离变小时候(即往右边移动),易知其AD与AB的夹角会变小,AD长度变小,根据勾股定理易知,斜边变小,其中一条直角边固定不变,则另一条直角边肯定会长度变小.
故答案为:变小.
【分析】可连接光源和人的头顶可知,墙上的影长和人到墙的距离变化规律是:距离墙越近,影长越短,距离墙越远影长越长.
10.在数学活动课上,老师带领数学小组测量大树 的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离 为2m,那么这棵大树高 m.
【答案】9
【知识点】平行投影
【解析】【解答】解:延长AD交BC延长线于E,
根据同一时刻影长与物高成比例可得CE:CD=1:1.4,
∵CD=2m,
∴CE= m,
∴BE=BC+CE=5+ = m,
∴BE:AB=1:1.4,
∴AB=9m.
故答案为:9.
【分析】根据同一时刻影长与物高成比例,先求出CE,再求AB即可.
11.如图,林林在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则该树的高度为
【答案】4m
【知识点】锐角三角函数的定义;平行投影
【解析】【解答】解:根据题意构建如图所示的三角形:
∴∠ECF=90°,ED=2 m,DF=8 m,CD为树高.
∵∠1+∠2=∠E+∠2=90°,
∴∠1=∠E.
∴tan E=tan∠ 1,
即 = ,
解得CD=4 m.
【分析】根据题意构建如图所示的三角形:根据同角的余角相等,再由等角的正切相等得 ,解之即可得出答案.
12.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为 m
【答案】5
【知识点】平行投影
【解析】【解答】解:小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
∵=,
∴=,解得GH=8,
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=GH=4,
在Rt△OGM中,OM=R﹣2,OG=R,GM=4,
∵OM2+GM2=OG2,
∴(R﹣2)2+42=R2,解得R=5,
即⊙O的半径为5m.
故答案为5m.
【分析】小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,先利用平行投影的性质和相似的性质得到=,于是可求出GH=8,再根据垂径定理得到点O在直线MN上,GM=HM=GH=4,然后根据勾股定理得到(R﹣2)2+42=R2,再解方程即可.
13.如图:(A)(B)(C)(D)是一天中四个不同时刻的木杆在地面上的影子,将它们按时间先后顺序进行排列,为 .
【答案】(D)(C)(A)(B)
【知识点】平行投影
【解析】【解答】解:太阳从东方升起最后从西面落下,木杆的影子应该在西面,随着时间的变化影子逐渐的向北偏西,南偏西,正东方向的顺序移动,故它们按时间先后顺序进行排列,为(D)(C)(A)(B).
【分析】根据影子变化的方向正好太阳所处的方向是相反的来判断.太阳从东方升起最后从西面落下确定影子的起始方向.
三、解答题(每小题8分,共48分)
14.如图,AB表示一个窗户的高,AM和BN表示射人室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,求窗户的高度AB.
【答案】解:∵BN∥AM,
∴∠CBN=∠A,∠CNB=∠M,
∴△CBN∽△CAM,
∴ 即
解得:CA=3,
∴AB=3-1=2,
答:窗户的高度AB为2m.
【知识点】相似三角形的性质;平行投影
【解析】【分析】阳光可看作一束平行光,由光的直线传播特性可知透过窗户后的光线BN与AE仍然平行,由此可得出一对相似三角形,由相似三角形的性质可求出AC的长,进而求出AB的长即窗户的高度.
15.如图,树、红旗、人在同一直线上,已知人的影子为AB,树的影子为CD,确定光源的位置并画出旗杆的影子.
【答案】解:如图所示是灯光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线,再过人的顶端及其影子的顶端作一条直线,两直线相交,其交点就是光源的位置;然后再过旗杆的顶端连接光源的直线,交地面于一点,连接这点与旗杆底端的线段就是旗杆的影子.
【知识点】平行投影
【解析】【分析】利用两个物体与影长的对应顶点的连线交于一点,这样得到的投影是中心投影,此点就是光源的位置所在.
16.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
【答案】解:(1)如图所示:P点即为路灯的位置;
(2)如图所示:GM即为所求.
【知识点】中心投影
【解析】【分析】(1)利用对应点连线相交于一点进而得出路灯位置;
(2)利用路灯的位置得出大树高.
17.如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°.(以下计算结果都保留根号)
(1)求影子EB的长;
(2)若∠SAC=60°,求光源S离开地面的高度.
【答案】解:(1)∵圆锥的底面半径和高都为2m,∴CH=HE=2m,∵∠SBA=30°,∴HB=2m,∴影长BE=BH﹣HE=2﹣2(m);(2)作CD⊥SA于点D,在Rt△ACD中,得CD=ACcos30°=AC=,∵∠SBA=30°,∠SAB=∠SAC+∠BAC=60°+45°=105°,∴∠DSC=45°,∴SC==2,∴SB=2+BC=2+4,∴SF=SB=(+2)m,答:光源S离开地面的高度为(2+)m.
【知识点】中心投影
【解析】【分析】(1)根据已知得出CH=HE=2m,进而得出HB的长,即可得出BE的长;
(2)首先求出CD的长进而得出∠DSC=45°,利用锐角三角函数关系得出SC的长即可.
18.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的.请你确定此时路灯光源的位置.
【答案】解:
∴点O为路灯光源的位置.
【知识点】中心投影
【解析】【分析】直接连接树的顶端和影子的顶端形成的直线,再根据反射的原理作出经过玻璃反射的光线形成的直线,两条直线的交点处即为点光源的位置.
19.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
【答案】解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴,即,解得DE=10(m),
即DE的长为10m.
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)连结AC,过点D作DF∥AC,则EF为所求;
(2)先证明Rt△ABC∽Rt△DEF,然后利用相似比计算出DE的长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
