人教版九年级数学下名师点拨与训练第28章 锐角三角函数29.2 三视图
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第28章 锐角三角函数29.2 三视图 |  | |
| 格式 | doc | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 11:20:53 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.2 三视图
学习目标:
1.会从投影的角度理解视图的概念;
2.会画简单几何体的三视图;
3.会利用三视图计算立体图形的侧面积和表面积
4.通过观察探究等活动知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系.
老师告诉你
1.由三视图想象立体图形,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面、左面,然后再综合起来考虑整体图形。
2.由物画图与由图想物是相互联系的两类问题,前者是“分解”,后者是“综合”,体会由三视图想象立体图形,感受“综合”思考过程.
一、知识点拨
知识点1 、 三视图概念及被观察物体三视图之间的关系:
三视图的概念
视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水 平面,右边的面叫做侧面.
(3)三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
被观察物体三视图之间的关系
(1)位置关系
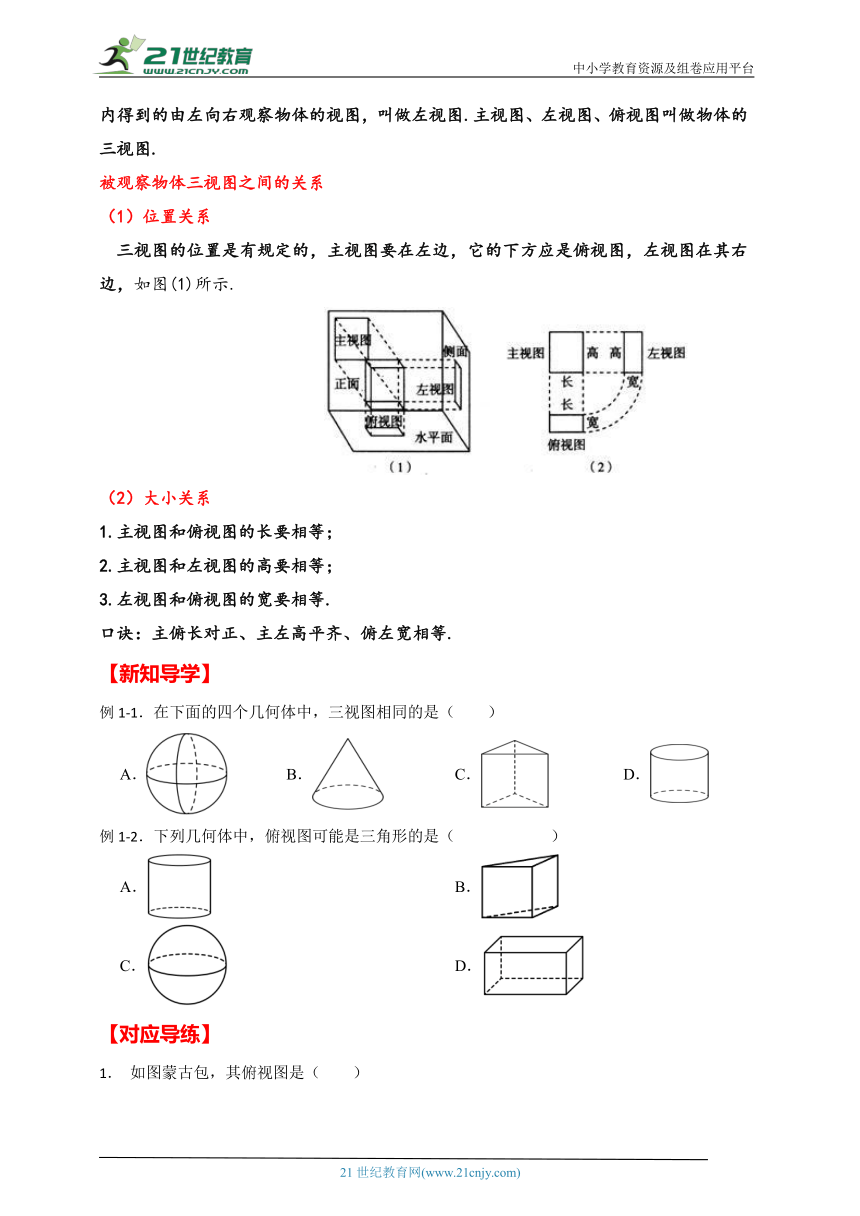
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
(2)大小关系
1.主视图和俯视图的长要相等;
2.主视图和左视图的高要相等;
3.左视图和俯视图的宽要相等.
口诀:主俯长对正、主左高平齐、俯左宽相等.
【新知导学】
例1-1.在下面的四个几何体中,三视图相同的是( )
A. B. C. D.
例1-2.下列几何体中,俯视图可能是三角形的是( )
A. B.
C. D.
【对应导练】
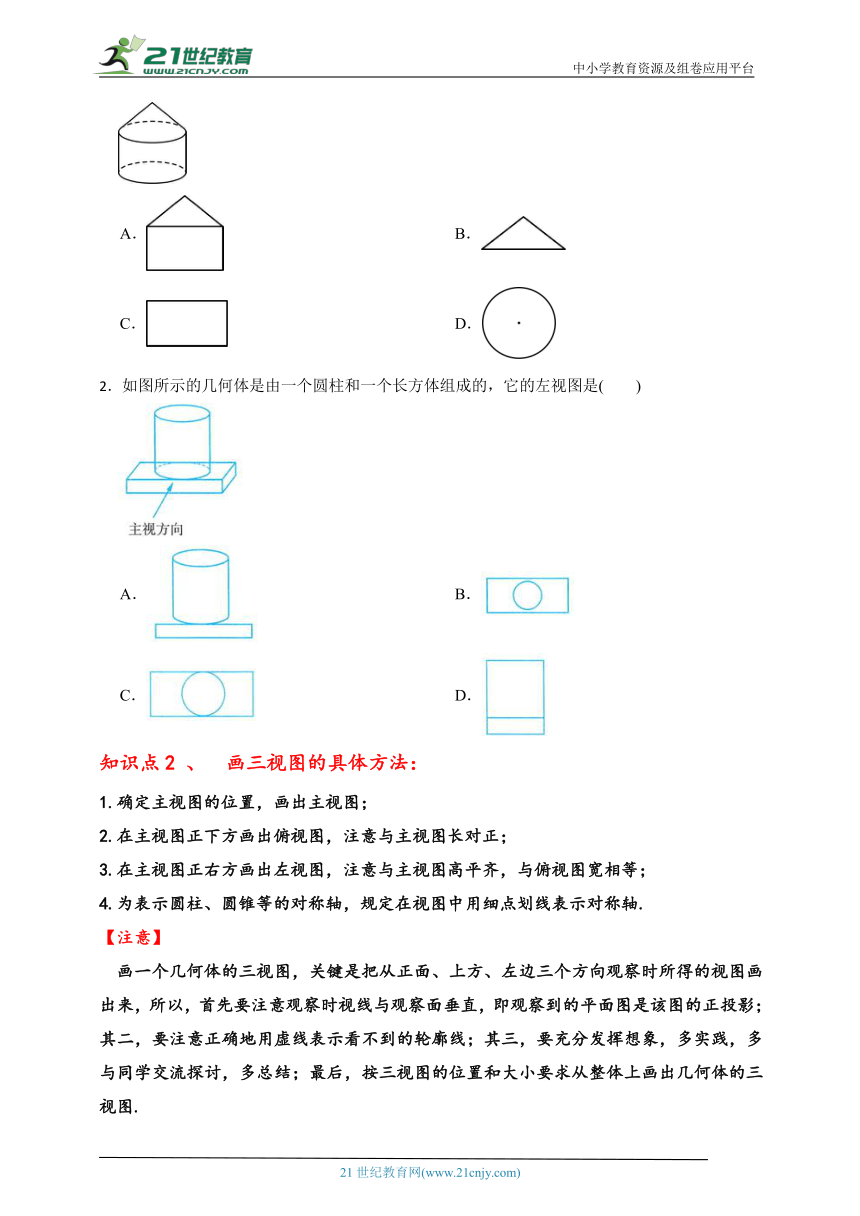
1. 如图蒙古包,其俯视图是( )
A. B.
C. D.
2.如图所示的几何体是由一个圆柱和一个长方体组成的,它的左视图是( )
A. B.
C. D.
知识点2 、 画三视图的具体方法:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图长对正;
3.在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
4.为表示圆柱、圆锥等的对称轴,规定在视图中用细点划线表示对称轴.
【注意】
画一个几何体的三视图,关键是把从正面、上方、左边三个方向观察时所得的视图画出来,所以,首先要注意观察时视线与观察面垂直,即观察到的平面图是该图的正投影;其二,要注意正确地用虚线表示看不到的轮廓线;其三,要充分发挥想象,多实践,多与同学交流探讨,多总结;最后,按三视图的位置和大小要求从整体上画出几何体的三视图.
【新知导学】
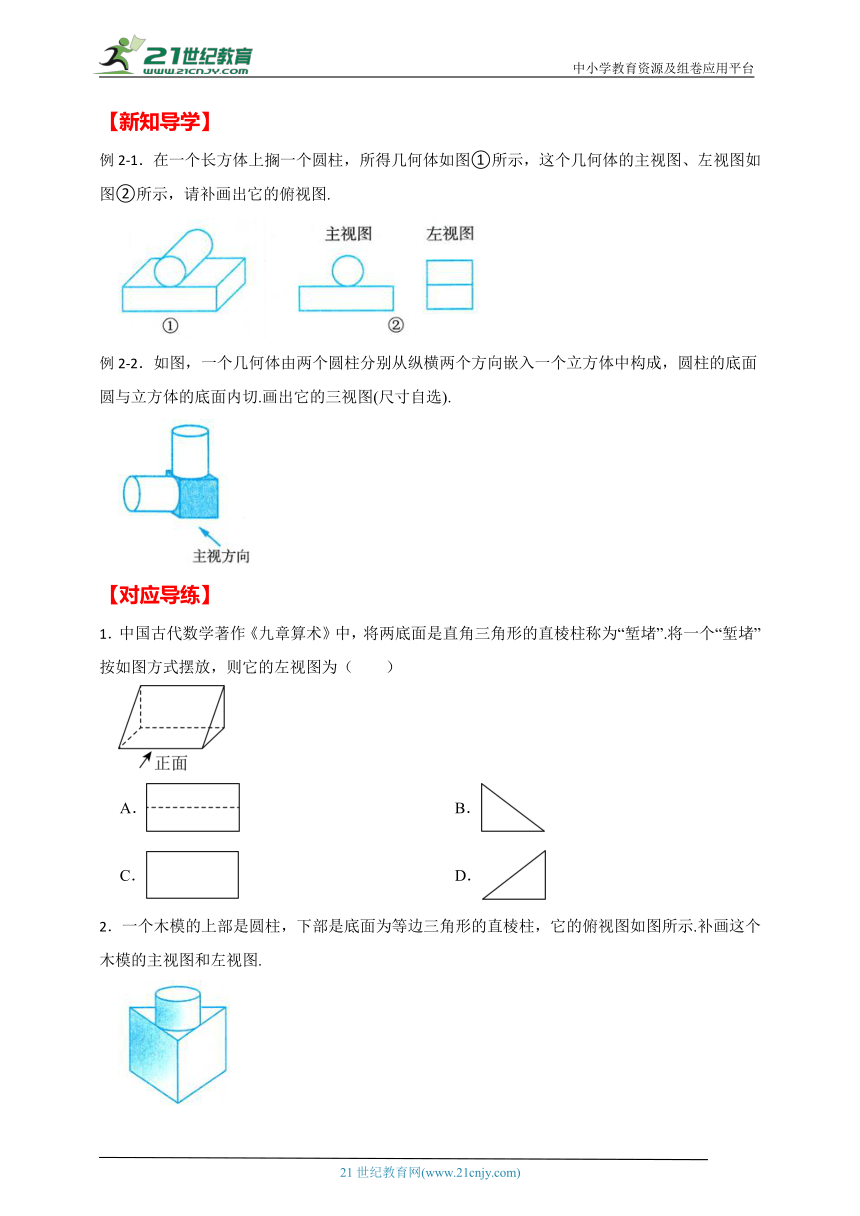
例2-1.在一个长方体上搁一个圆柱,所得几何体如图①所示,这个几何体的主视图、左视图如图②所示,请补画出它的俯视图.
例2-2.如图,一个几何体由两个圆柱分别从纵横两个方向嵌入一个立方体中构成,圆柱的底面圆与立方体的底面内切.画出它的三视图(尺寸自选).
【对应导练】
1.中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的左视图为( )
A. B.
C. D.
2.一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱,它的俯视图如图所示.补画这个木模的主视图和左视图.
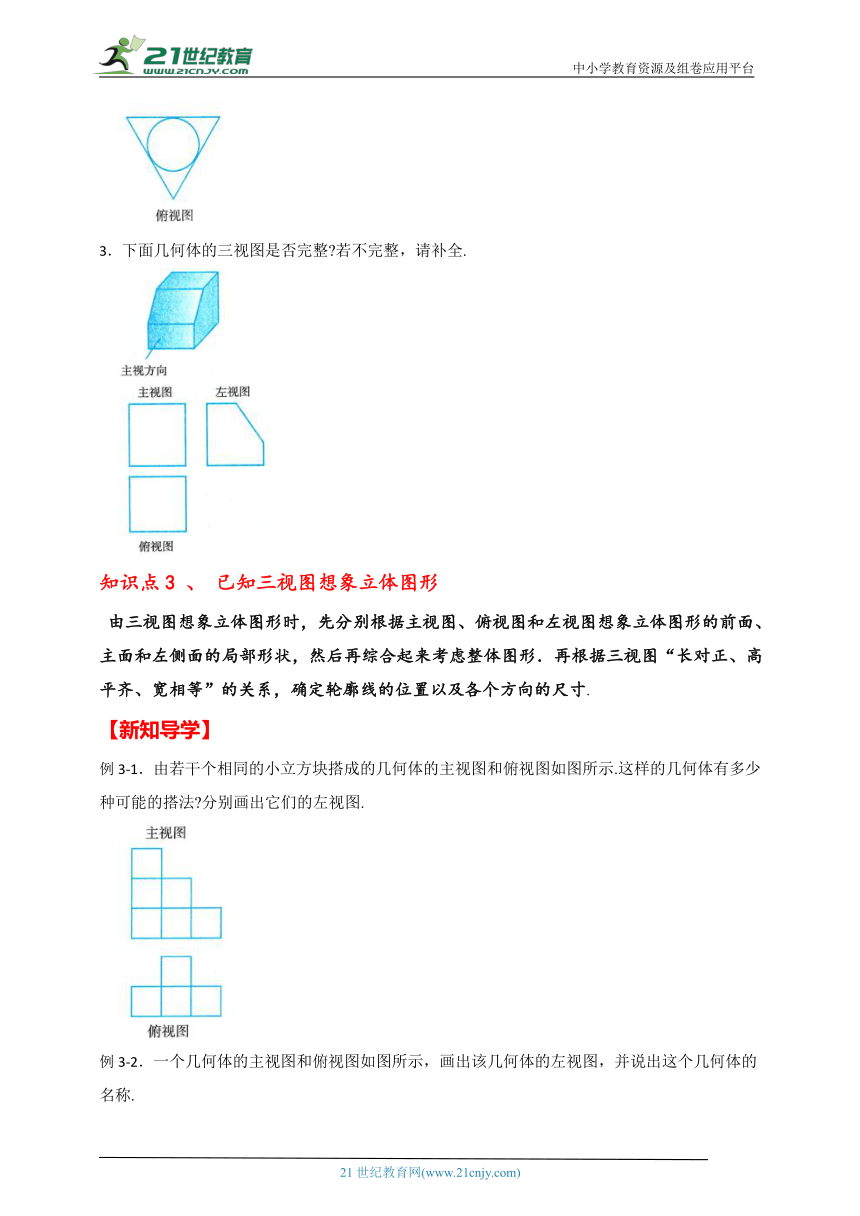
3.下面几何体的三视图是否完整 若不完整,请补全.
知识点3 、 已知三视图想象立体图形
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置以及各个方向的尺寸.
【新知导学】
例3-1.由若干个相同的小立方块搭成的几何体的主视图和俯视图如图所示.这样的几何体有多少种可能的搭法 分别画出它们的左视图.
例3-2.一个几何体的主视图和俯视图如图所示,画出该几何体的左视图,并说出这个几何体的名称.
【对应导练】
1.如图是某个几何体的三视图,则这个几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
2. 如图是某几何体的主视图、左视图和俯视图,则该几何体是( )
A.球 B.圆柱 C.圆锥 D.长方体
3.如图是一个几何体的三视图,则该几何体是( )
A. B.
C. D.
4.一个几何体的三视图如图所示,这个几何体是 .
知识点4 、 由三视图求立体图形的面积(体积)
1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
2)将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
3)最后根据已知数据,求出展开图的面积(体积).
【新知导学】
例4-1.下图是一个几何体的三视图.
(1)说出这个几何体的名称.
(2)请根据图中尺寸(单位:cm)求该几何体的全面积(结果保留π).
例4-2.已知某几何体的三视图如下,其中俯视图为正方形,则这个长方体的底面边长为 .
二、题型训练
1.画几何体的三视图
1.如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
A. B.
C. D.
2.如图所示的几何体的主视图是( )
A. B.
C. D.
3.如图所示的几何体的俯视图是( )
A. B. C. D.
由三视图确定几何体
4.如图是由几个小立方块所搭成的几何体从上面所看到的,小正方形中的数字表示在该方块的个数,则从左边看到的这个几何体的形状图为( )
A. B.
C. D.
5.一个几何体由若干个大小相同的小立方块搭成,如图分别是它的主视图和俯视图,若该几何体所用小立方块的个数为个,则的最小值为( )
A.9 B.11 C.12 D.13
3.由三视图确定几何体的表面积
6.如图是一几何体的三视图,请选择恰当的比例,画出其表面展开图,并计算它的侧面积与全面积.
7.如图是某几何体的三视图,则该几何体的体积是( )
A.. B.. C.. D..
8.由7个完全相同的小立方体搭成的几何体如下,每个小正方体的棱长为2cm.
(1)画出该几何体的三视图(比例自选).
(2)求出该几何体的表面积.
9.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是 .
三、课堂达标
一、选择题(每小题4分,共32分)
1.由6个同样的立方体摆出从正面看是 的几何体,下面摆法正确的是( )
A. B.
C. D.
2.如图是大小相同的5个正方体搭成的几何体,其左视图是( )
A. B.
C. D.
3.下列四个几何体中,左视图为圆的是( )
A. B.
C. D.
4.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,这种连接方式不但可以承受较大的荷载,而且允许产生一定的变形.右图是某种榫卯构件的示意图,其中榫的俯视图是( )
A. B.
C. D.
5.如图的几何体是由10个相同的小正方体搭成的,若移走下列中的一块小正方体后,该几何体的主视图会发生改变,则可能移走的是( )
A.① B.② C.③ D.④
6.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不相同的几何体是( )
A.①② B.②③ C.②④ D.③④
7.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A.108cm3 B.100 cm3 C.92cm3 D.84cm3
8.某三棱锥的三视图如图所示,该三棱锥的体积是( )
A. B.4 C.2 D.
二、填空题(每小题4分,共20分)
9.桌上放着一个圆锥和长方体的组合体(如图①),图②③④是它的三视图,请在下面横线上写出三个视图的名称.
. . .
10.由个大小相同的小立方块搭成的几何体的左视图和俯视图如图所示,则的值为 .
11.一个长方体的三种视图如图所示,若其俯视图为正方形,则这个长方体的体积为 .
12.下图是由若干个相同的小正方体组合而成的一个几何体的三视图,则组成这个几何体的小正方体个数是 .
13.如图,是一几何体的三视图,根据图中数据,这个几何体的侧面积是 .
三、解答题(每小题8分,共48分)
14.按如图所标的主视方向填写下列几何体的三视图的名称.
圆柱 圆锥 球
主视图
俯视图
左视图
15.如图是一个直三棱柱的立体图和三视图,根据立体图上的尺寸,求:
(1)三视图中AB的长.
(2)左视图的面积.
16.已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.
17.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所示尺寸(单位:mm),计算出这个立体图形的表面积.
18.已知一个几何体的三视图如图所示,则该几何体的体积为多少?
19.分别画出如图所示几何体的三视图,并求几何体的表面积和体积.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.2 三视图
学习目标:
1.会从投影的角度理解视图的概念;
2.会画简单几何体的三视图;
3.会利用三视图计算立体图形的侧面积和表面积
4.通过观察探究等活动知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系.
老师告诉你
1.由三视图想象立体图形,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面、左面,然后再综合起来考虑整体图形。
2.由物画图与由图想物是相互联系的两类问题,前者是“分解”,后者是“综合”,体会由三视图想象立体图形,感受“综合”思考过程.
一、知识点拨
知识点1 、 三视图概念及被观察物体三视图之间的关系:
三视图的概念
视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水 平面,右边的面叫做侧面.
(3)三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
被观察物体三视图之间的关系
(1)位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
(2)大小关系
1.主视图和俯视图的长要相等;
2.主视图和左视图的高要相等;
3.左视图和俯视图的宽要相等.
口诀:主俯长对正、主左高平齐、俯左宽相等.
【新知导学】
例1-1.在下面的四个几何体中,三视图相同的是( )
A. B. C. D.
【答案】A
【知识点】简单几何体的三视图
【解析】【解答】解:A、球的主视图,俯视图,左视图都是圆,符合题意;
B、圆锥的主视图和左视图都是三角形,俯视图是圆,不符合题意;
C、三棱柱的主视图和左视图都是长方形,俯视图是三角形,不符合题意;
D、圆柱的主视图和左视图都是长方形,俯视图是圆,不符合题意.
故答案为:A.
【分析】主视图,就是从前向后看得到的正投影;左视图,就是从左向右看得到的正投影;俯视图,就是从上向下看得到的正投影,根据定义分别找出各个几何体的三个视图,即可逐一判断得出答案.
例1-2.下列几何体中,俯视图可能是三角形的是( )
A. B.
C. D.
【答案】B
【知识点】简单几何体的三视图
【解析】【解答】根据题意,俯视图可能是三角形的是
故选B.
【分析】根据俯视图的意义解答可.
【对应导练】
1. 如图蒙古包,其俯视图是( )
A. B.
C. D.
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:从上面看,俯视图为一个带圆心的圆,
即 .
故答案为:D.
【分析】根据俯视图是从上面看到的图形,即可得到答案.
2.如图所示的几何体是由一个圆柱和一个长方体组成的,它的左视图是( )
A. B.
C. D.
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:这个组合体的左视图为:
故答案为:D.
【分析】画出这个组合体的左视图即可求解.
知识点2 、 画三视图的具体方法:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图长对正;
3.在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
4.为表示圆柱、圆锥等的对称轴,规定在视图中用细点划线表示对称轴.
【注意】
画一个几何体的三视图,关键是把从正面、上方、左边三个方向观察时所得的视图画出来,所以,首先要注意观察时视线与观察面垂直,即观察到的平面图是该图的正投影;其二,要注意正确地用虚线表示看不到的轮廓线;其三,要充分发挥想象,多实践,多与同学交流探讨,多总结;最后,按三视图的位置和大小要求从整体上画出几何体的三视图.
【新知导学】
例2-1.在一个长方体上搁一个圆柱,所得几何体如图①所示,这个几何体的主视图、左视图如图②所示,请补画出它的俯视图.
【答案】解:如图所示.
【知识点】作图﹣三视图
【解析】【分析】根据简单组合体的三视图画法画出俯视图即可.
例2-2.如图,一个几何体由两个圆柱分别从纵横两个方向嵌入一个立方体中构成,圆柱的底面圆与立方体的底面内切.画出它的三视图(尺寸自选).
【答案】
【知识点】作图﹣三视图
【解析】【分析】根据简单组合体的三视图画法画出相应图形即可.
【对应导练】
1.中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的左视图为( )
A. B.
C. D.
【答案】B
【知识点】简单几何体的三视图
【解析】【解答】解:从左边观看立体图形可得:左视图为直角在左边的直角三角形,
故选:B.
【分析】左视图:从物体左面所看的平面图形,注意:看到的棱画实线,看不到的棱画虚线,据此进行解答即可.
2.一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱,它的俯视图如图所示.补画这个木模的主视图和左视图.
【答案】解:如图所示,
【知识点】作图﹣三视图
【解析】【分析】根据三视图的画法即可画出相应图形.
3.下面几何体的三视图是否完整 若不完整,请补全.
【答案】解:该几何体的三视图不完成,补全图形如下图.
【知识点】简单几何体的三视图;作图﹣三视图
【解析】【分析】 根据几何体的三视图画法画出图形,注意看得见部分的轮廓线画成实线,被遮挡部分的轮廓线画成虚线即可.
知识点3 、 已知三视图想象立体图形
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置以及各个方向的尺寸.
【新知导学】
例3-1.由若干个相同的小立方块搭成的几何体的主视图和俯视图如图所示.这样的几何体有多少种可能的搭法 分别画出它们的左视图.
【答案】解:这样的几何体有3种可能.左视图的示意图如图
【知识点】作图﹣三视图;由三视图判断小正方体的个数
【解析】【分析】根据主视图,俯视图,想像出几何体,再根据几体体画出左视图.
例3-2.一个几何体的主视图和俯视图如图所示,画出该几何体的左视图,并说出这个几何体的名称.
【答案】解:左视图
该几何体是直三棱柱.
【知识点】由三视图判断几何体;作图﹣三视图
【解析】【分析】根据俯视图三角形水平边上的高与主视图较短边为长与宽画出左视图.
【对应导练】
1.如图是某个几何体的三视图,则这个几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
【答案】D
【知识点】由三视图判断几何体
【解析】【解答】解:根据三视图的定义可得,该图形是三棱柱的三视图,
故答案为:D.
【分析】利用三棱柱三视图的特征分析求解即可.
2. 如图是某几何体的主视图、左视图和俯视图,则该几何体是( )
A.球 B.圆柱 C.圆锥 D.长方体
【答案】C
【知识点】由三视图判断几何体
【解析】【解答】解:∵主视图及左视图是三角形,
∴该几何体应该是椎体,
∵俯视图是圆形,
∴该几何体是圆锥.
故答案为:C.
【分析】由主视图及左视图可判断出是柱体还是椎体,再结合俯视图即可判断出是圆锥.
3.如图是一个几何体的三视图,则该几何体是( )
A. B.
C. D.
【答案】C
【知识点】由三视图判断几何体
【解析】【解答】解:A:主视图为:,不符合题意;
B:主视图为:,不符合题意;
C:主视图为:,符合题意;
D:主视图为:,不符合题意
故答案为:C
【分析】根据组合体的三视图,分别求出各项主视图即可求出答案.
4.一个几何体的三视图如图所示,这个几何体是 .
【答案】圆柱
【知识点】由三视图判断几何体
【解析】【解答】解:一个几何体的三视图中,主视图与左视图都是矩形,俯视图是圆,这个几何体是圆柱.
故答案为:圆柱.
【分析】根据所给的三视图,想像几何体.
知识点4 、 由三视图求立体图形的面积(体积)
1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
2)将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
3)最后根据已知数据,求出展开图的面积(体积).
【新知导学】
例4-1.下图是一个几何体的三视图.
(1)说出这个几何体的名称.
(2)请根据图中尺寸(单位:cm)求该几何体的全面积(结果保留π).
【答案】(1)解:该几何体为一个圆锥.
(2)解:由(1)可得:该几何题为圆锥,
底面圆半径r=12,高为6,
∴侧面母线长
∴
【知识点】圆锥的计算;由三视图判断几何体
【解析】【分析】(1)根据三视图的特征结合圆锥特征即可求出答案.
(2)根据勾股定理求出圆锥侧面母线长,再根据圆锥全面积公式即可求出答案.
例4-2.已知某几何体的三视图如下,其中俯视图为正方形,则这个长方体的底面边长为 .
【答案】2
【知识点】勾股定理;简单几何体的三视图
【解析】【解答】解:由主视图可得底面正方形对角线长为
设底面正方形边长为a
∴
解得:a=2
故答案为:2
【分析】根据主视图可得出底面正方形对角线,再根据勾股定理即可求出答案.
二、题型训练
1.画几何体的三视图
1.如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
A. B.
C. D.
【答案】C
【知识点】简单组合体的三视图;小正方体组合体的三视图
【解析】【解答】解:俯视图为:.
故答案为:C.
【分析】俯视图是从几何体上面观察所得到的平面图形,据此判断.
2.如图所示的几何体的主视图是( )
A. B.
C. D.
【答案】A
【知识点】简单组合体的三视图
【解析】【解答】解:此题是一个圆柱与一个六棱柱的组合体,其主视图应该为:下面是一个矩形左右各加一竖实线,上面是一个矩形所以只有A选项符合题意.
故答案为:A.
【分析】主视图,就是从正面看得到的图形,看得见的轮廓线需要画成实线,看不见但又存在的轮廓线画成虚线,据此可的A选项是其主视图,B选项是其左视图,C选项是其俯视图.
3.如图所示的几何体的俯视图是( )
A. B. C. D.
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:从上面看该几何体,选项D的图形符合题意,
故答案为:D.
【分析】俯视图是从几何体上面观察所得到的平面图形,据此判断.
由三视图确定几何体
4.如图是由几个小立方块所搭成的几何体从上面所看到的,小正方形中的数字表示在该方块的个数,则从左边看到的这个几何体的形状图为( )
A. B.
C. D.
【答案】B
【知识点】由三视图判断几何体
【解析】【解答】解:观察俯视图可知,这个几何体的左视图由3列小正方形组成,最左列只有一个正方形,中间列有3个,最右边一列有2个,
故答案为:B.
【分析】本题考查的是几何体的三视图,由条件中的俯视图可以判断出几何体的形状,再以此推断出几何体的左视图.
5.一个几何体由若干个大小相同的小立方块搭成,如图分别是它的主视图和俯视图,若该几何体所用小立方块的个数为个,则的最小值为( )
A.9 B.11 C.12 D.13
【答案】A
【知识点】由三视图判断几何体
【解析】【解答】解:根据主视图、俯视图可得:当小立方块个数最少时,在俯视图的相应位置上所摆放的个数如下:
故n的最小值为1+1+1+1+2+3=9.
故答案为:9.
【分析】根据主视图、俯视图可得:当小立方块个数最少时,每层摆放的个数,然后相加即可.
3.由三视图确定几何体的表面积
6.如图是一几何体的三视图,请选择恰当的比例,画出其表面展开图,并计算它的侧面积与全面积.
【答案】表面展开图如图所示
它的侧面积是(1.5+2+2.5)×3=18(cm2);
它的全面积是18+×1.5×2×2=21(cm2)
【知识点】几何体的表面积;几何体的展开图;由三视图判断几何体
【解析】【分析】根据三视图可知,这个几何体是三棱柱,据此画出展开图,求出侧面积,全面积即可.
7.如图是某几何体的三视图,则该几何体的体积是( )
A.. B.. C.. D..
【答案】C
【知识点】简单组合体的三视图
【解析】【解答】解:根据题意可知该几何体是六棱柱,且底面是正六边形,
将正六边形分成6个全等的等边三角形,过点A作AD⊥BC于点D,如图,
由题意得AB=BC=5,BD=2.5,
∴根据勾股定理得,
∴,
∴正六边形得面积为,
∵由题意得六棱柱的高为2,
∴该几何体六棱柱的体积是.
故答案为:C.
【分析】先根据题意得到该几何体是六棱柱,且底面是正六边形,根据棱柱的体积公式是V=Sh(S是底面积,h是棱柱的高),可先求出底面积,把它分成6个全等的等边三角形去求,利用勾股定理求出等边三角形的高即可求出底面积,最后再代入体积公式即可求出答案.
8.由7个完全相同的小立方体搭成的几何体如下,每个小正方体的棱长为2cm.
(1)画出该几何体的三视图(比例自选).
(2)求出该几何体的表面积.
【答案】(1)解:画三视图如下.
(2)解:S表面=(5+3+5)×2×2×2+2×2×2=112(cm2).
【知识点】作图﹣三视图;小正方体组合体的表面积
【解析】【分析】(1)直接根据立体图形画出三视图即可;
(2)由立体图形可知,正面有5个面,后面有5个面,上面有5个面,底面有5个面,左面有3个面,右面有3个面,中间内侧有2个面,即(5+3+5)×2×2×2+2×2×2=112(cm2).
9.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是 .
【答案】12π
【知识点】圆锥的计算;由三视图判断几何体;圆柱的侧面积和表面积
【解析】【解答】解:由三视图可得该结合体上面是圆锥,下面是圆柱,
根据三视图中的数据可得圆锥的母线长为=2,
∴该整流罩的侧面积为π×2.4×4+π×(2.4÷2)×2=12π.
故答案为:12π.
【分析】由三视图可得该结合体上面是圆锥,下面是圆柱,根据三视图中的数据求出圆锥的母线长,然后根据圆柱、圆锥的侧面积公式进行计算.
三、课堂达标
一、选择题(每小题4分,共32分)
1.由6个同样的立方体摆出从正面看是 的几何体,下面摆法正确的是( )
A. B.
C. D.
【答案】B
【知识点】简单几何体的三视图
【解析】【解答】解:A、主视图得到两行两列,故A不符合题意
B、主视图是,故B符合题意
C、主视图是两行三列,且第一二列都是两个,故C不符合题意
D、主视图是两行四列,故D不符合题意
故答案为:B.
【分析】从一个几何体正面投射得到的视图叫几何体的主视图.
2.如图是大小相同的5个正方体搭成的几何体,其左视图是( )
A. B.
C. D.
【答案】A
【知识点】简单组合体的三视图
【解析】【解答】解:根据立体图可知该左视图是底层有2个小正方形,第二层左边有1个小正方形.
故选:A.
【分析】从左边观察即可判断.
3.下列四个几何体中,左视图为圆的是( )
A. B.
C. D.
【答案】A
【知识点】简单几何体的三视图
【解析】【解答】解:左视图为从左往右看得到的视图,
A.球的左视图是圆,
B.圆柱的左视图是长方形,
C.圆锥的左视图是等腰三角形,
D.圆台的左视图是等腰梯形,
故答案为:A.
【分析】根据三视图的定义求解即可。
4.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,这种连接方式不但可以承受较大的荷载,而且允许产生一定的变形.右图是某种榫卯构件的示意图,其中榫的俯视图是( )
A. B.
C. D.
【答案】D
【知识点】简单几何体的三视图
【解析】【解答】解:从上往下看立体图,可以得到俯视图的形状应该是四根实线夹着两根虚线的长方形,如图所示:
故选:D.
【分析】利用几何体俯视图的定义(从上面观察物体所得到的视图是俯视图)分析求解即可.
5.如图的几何体是由10个相同的小正方体搭成的,若移走下列中的一块小正方体后,该几何体的主视图会发生改变,则可能移走的是( )
A.① B.② C.③ D.④
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:由几何体的搭建可知,若移走下列中的一块小正方体后,该几何体的主视图会发生改变,则可能移走的小正方体是④.
故答案为:D.
【分析】根据主视图是从正面看到的图像即可判断.
6.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不相同的几何体是( )
A.①② B.②③ C.②④ D.③④
【答案】B
【知识点】简单几何体的三视图
【解析】【分析】先分别分析四种几何体的三种视图,再找出有两个相同而另一个不同的几何体.
【解答】①因为正方体的三个视图都相同,都是正方形,不符合条件;
②圆柱的主视图与左视图都是长方形,俯视图是圆,符合条件;
③圆锥的主视图与左视图都是三角形,俯视图是圆中间还有一点,符合条件;
④球的三个视图都相同,都是圆,不符合条件.
故符合条件的是:②③.
故选:B.
【点评】此题主要考查了学生的观察能力和对几何体三种视图的空间想象能力
7.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A.108cm3 B.100 cm3 C.92cm3 D.84cm3
【答案】B
【知识点】由三视图判断几何体
【解析】【解答】解:由三视图可知:该几何体是一个棱长分别为6cm,6cm,3cm的长方体截去一个三条侧棱长分别为4cm,4cm,3cm的一个三棱锥(长方体的一个角)后的图形,如图所示.
∴该几何体的体积V=6×6×3-
=100(cm3).
故答案为B。
【分析】从三视图,若不看每个图中斜的实线,我们会发现该几何体是一个长方体;根据斜线的位置可以确定该几何体是由一个长方体截掉一个棱锥所得到的。由三视图得到长方体的长、宽、高,以及三棱锥的底面三角形的底与高,和三棱锥的高。
8.某三棱锥的三视图如图所示,该三棱锥的体积是( )
A. B.4 C.2 D.
【答案】B
【知识点】由三视图判断几何体
【解析】【解答】解:由主视图和俯视图,底面三角形一条边长为4,
由左视图可得底面三角形边长为4的边对应的高长为3,且三棱锥的高是2,
则三棱锥的体积是
故答案为:B。
【分析】由三棱锥的体积公式,则需要求出底面的面积及三棱锥的高;由主视图和俯视图,底面三角形一条边长为4;由左视图可得底面三角形边长为4的边对应的高长为3,且三棱锥的高是2,从而代入公式计算即可。
二、填空题(每小题4分,共20分)
9.桌上放着一个圆锥和长方体的组合体(如图①),图②③④是它的三视图,请在下面横线上写出三个视图的名称.
. . .
【答案】俯视图;左视图;主视图
【知识点】简单组合体的三视图
【解析】【解答】解: 根据题意得,图 ② 是该几何体的俯视图;图 ③是该几何体的左视图;图 ④ 是该几何体的主视图.
故答案为:俯视图;左视图;主视图.
【分析】根据三视图的概念,观察几何体后即可得出答案.
10.由个大小相同的小立方块搭成的几何体的左视图和俯视图如图所示,则的值为 .
【答案】6或7
【知识点】简单组合体的三视图;由三视图判断小正方体的个数
【解析】【解答】解:根据俯视图有5个正方形,可知几何体至少有5个小立方体,再根据左视图,可知几何体还可能有1或2个小立方体,故n的值为6或7.
故答案为:6或7.
【分析】先根据俯视图,得出n至少有几个,再根据左视图可得还可能有几个,再求n.
11.一个长方体的三种视图如图所示,若其俯视图为正方形,则这个长方体的体积为 .
【答案】144
【知识点】简单几何体的三视图;由三视图判断几何体
【解析】【解答】由图形可得长方体体积为,
【分析】根据对角线为6cm,俯视图是一个长方形,则地面面积为(cm2),再根据长方体体积公式计算即可.
12.下图是由若干个相同的小正方体组合而成的一个几何体的三视图,则组成这个几何体的小正方体个数是 .
【答案】5
【知识点】由三视图判断几何体
【解析】【解答】解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,
第二有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
故答案为:5.
【分析】 根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
13.如图,是一几何体的三视图,根据图中数据,这个几何体的侧面积是 .
【答案】
【知识点】圆锥的计算;由三视图判断几何体
【解析】【解答】解:由三视图可知,原几何体为圆锥,
∵圆锥的底面半径为: ,圆锥的高为: ,
∴圆锥的母线长为: ,
∴ ;
∴这个几何体的侧面积是 ;
故答案为: .
【分析】根据三视图的定义判断出该物体为圆锥,再利用圆锥的侧面积计算即可。
三、解答题(每小题8分,共48分)
14.按如图所标的主视方向填写下列几何体的三视图的名称.
圆柱 圆锥 球
主视图
俯视图
左视图
【答案】
圆柱 圆锥 球
主视图 矩形 等腰三角形 圆
俯视图 圆 圆和圆心 圆
左视图 矩形 等腰三角形 圆
【知识点】简单几何体的三视图
【解析】【分析】根据圆柱图、圆锥、球体的三视图进行填空即可解答.
15.如图是一个直三棱柱的立体图和三视图,根据立体图上的尺寸,求:
(1)三视图中AB的长.
(2)左视图的面积.
【答案】(1)解:如图,根据题意可知AC=AD=5,DC=6,过点D作DB⊥AC于点B,
设AB=x,则BC=5-x,
在与中,根据勾股定理得AD2-AB2=CD2-CB2,
∴52-x2=62-(5-x)2,
∴,即三视图中AB的长为;
(2)解:由(1)有,
∴在中,,
∴左视图面积为.
【知识点】简单几何体的三视图
【解析】【分析】(1)利用俯视图, 如图所示,AC=AD=5,DC=6,过点D作DB⊥AC于点B,设AB=x,根据勾股定理构建方程求解即可;
(2)左视图是一个长方形,根据题意得两边长的长度,再利用面积公式求解即可.
16.已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.
【答案】解:如图所示:根据三视图可以得出:此物体是:三棱柱表面积:S表=6×8+4×6+4×8+4×10=144(cm2);体积:V=×6×8×4=96(cm3).
【知识点】由三视图判断几何体
【解析】【分析】根据三视图得出几何体的各边长度,进而得出几何体的表面积和体积即可.
17.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所示尺寸(单位:mm),计算出这个立体图形的表面积.
【答案】解:根据三视图可得:上面的长方体长4mm,高4mm,宽2mm,
下面的长方体长8mm,宽6mm,高2mm,
∴立体图形的表面积是:4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2).
故答案为200 mm2.
【知识点】由三视图判断几何体
【解析】【分析】根据三视图可知立体图形下面的长方体的长、宽、高分别 8mm,6mm,2mm,上面的长、宽、高分别 4mm,2mm,4mm。由此计算这个立体图形的表面积即可。
18.已知一个几何体的三视图如图所示,则该几何体的体积为多少?
【答案】解:由三视图可其看成为两个长方体上、下叠放而成。
下面的长方体的长、宽、高分别为5、5、4;
上面的长方体的长、宽、高分别为5、4、1;
则该组合体的体积是5×5×4+5×4×1=120.
【知识点】由三视图判断几何体
【解析】【分析】由三视图将该几何看成是由两个长方体靠右对齐叠放而成;由标出的数据确定每个长方体的长宽高,从而计算两个长方体的体积和。
19.分别画出如图所示几何体的三视图,并求几何体的表面积和体积.
【答案】解:①
由勾股定理易得主视图中等腰三角形的腰长为5cm,
表面积为:6×2×2+8×2×2+2×6×4÷2+2×5×8+6×8=208cm2;
体积为:(6×2+6×4÷2)×8=192cm3;
②
表面积为:9×4.5×2+4.5×9×2+(4.5×4.5﹣1.5×3)×2+3×9×2=247.5cm2;
体积为:(4.5×4.5﹣1.5×3)×9=141.75cm3;
③
表面积为:15×5×2+10×15+(2×10×5﹣π×32)+ π(10﹣2﹣2)×15=(460+36π)cm2;
体积为:(10×5﹣ π×32)×15=(750﹣67.5π)cm3.
【知识点】作图﹣三视图
【解析】【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;计算表面积找到所有面的和相加即可;所给几何体的体积均为相应的底面积乘高,把相关数值代入即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.2 三视图
学习目标:
1.会从投影的角度理解视图的概念;
2.会画简单几何体的三视图;
3.会利用三视图计算立体图形的侧面积和表面积
4.通过观察探究等活动知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系.
老师告诉你
1.由三视图想象立体图形,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面、左面,然后再综合起来考虑整体图形。
2.由物画图与由图想物是相互联系的两类问题,前者是“分解”,后者是“综合”,体会由三视图想象立体图形,感受“综合”思考过程.
一、知识点拨
知识点1 、 三视图概念及被观察物体三视图之间的关系:
三视图的概念
视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水 平面,右边的面叫做侧面.
(3)三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
被观察物体三视图之间的关系
(1)位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
(2)大小关系
1.主视图和俯视图的长要相等;
2.主视图和左视图的高要相等;
3.左视图和俯视图的宽要相等.
口诀:主俯长对正、主左高平齐、俯左宽相等.
【新知导学】
例1-1.在下面的四个几何体中,三视图相同的是( )
A. B. C. D.
例1-2.下列几何体中,俯视图可能是三角形的是( )
A. B.
C. D.
【对应导练】
1. 如图蒙古包,其俯视图是( )
A. B.
C. D.
2.如图所示的几何体是由一个圆柱和一个长方体组成的,它的左视图是( )
A. B.
C. D.
知识点2 、 画三视图的具体方法:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图长对正;
3.在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
4.为表示圆柱、圆锥等的对称轴,规定在视图中用细点划线表示对称轴.
【注意】
画一个几何体的三视图,关键是把从正面、上方、左边三个方向观察时所得的视图画出来,所以,首先要注意观察时视线与观察面垂直,即观察到的平面图是该图的正投影;其二,要注意正确地用虚线表示看不到的轮廓线;其三,要充分发挥想象,多实践,多与同学交流探讨,多总结;最后,按三视图的位置和大小要求从整体上画出几何体的三视图.
【新知导学】
例2-1.在一个长方体上搁一个圆柱,所得几何体如图①所示,这个几何体的主视图、左视图如图②所示,请补画出它的俯视图.
例2-2.如图,一个几何体由两个圆柱分别从纵横两个方向嵌入一个立方体中构成,圆柱的底面圆与立方体的底面内切.画出它的三视图(尺寸自选).
【对应导练】
1.中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的左视图为( )
A. B.
C. D.
2.一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱,它的俯视图如图所示.补画这个木模的主视图和左视图.
3.下面几何体的三视图是否完整 若不完整,请补全.
知识点3 、 已知三视图想象立体图形
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置以及各个方向的尺寸.
【新知导学】
例3-1.由若干个相同的小立方块搭成的几何体的主视图和俯视图如图所示.这样的几何体有多少种可能的搭法 分别画出它们的左视图.
例3-2.一个几何体的主视图和俯视图如图所示,画出该几何体的左视图,并说出这个几何体的名称.
【对应导练】
1.如图是某个几何体的三视图,则这个几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
2. 如图是某几何体的主视图、左视图和俯视图,则该几何体是( )
A.球 B.圆柱 C.圆锥 D.长方体
3.如图是一个几何体的三视图,则该几何体是( )
A. B.
C. D.
4.一个几何体的三视图如图所示,这个几何体是 .
知识点4 、 由三视图求立体图形的面积(体积)
1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
2)将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
3)最后根据已知数据,求出展开图的面积(体积).
【新知导学】
例4-1.下图是一个几何体的三视图.
(1)说出这个几何体的名称.
(2)请根据图中尺寸(单位:cm)求该几何体的全面积(结果保留π).
例4-2.已知某几何体的三视图如下,其中俯视图为正方形,则这个长方体的底面边长为 .
二、题型训练
1.画几何体的三视图
1.如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
A. B.
C. D.
2.如图所示的几何体的主视图是( )
A. B.
C. D.
3.如图所示的几何体的俯视图是( )
A. B. C. D.
由三视图确定几何体
4.如图是由几个小立方块所搭成的几何体从上面所看到的,小正方形中的数字表示在该方块的个数,则从左边看到的这个几何体的形状图为( )
A. B.
C. D.
5.一个几何体由若干个大小相同的小立方块搭成,如图分别是它的主视图和俯视图,若该几何体所用小立方块的个数为个,则的最小值为( )
A.9 B.11 C.12 D.13
3.由三视图确定几何体的表面积
6.如图是一几何体的三视图,请选择恰当的比例,画出其表面展开图,并计算它的侧面积与全面积.
7.如图是某几何体的三视图,则该几何体的体积是( )
A.. B.. C.. D..
8.由7个完全相同的小立方体搭成的几何体如下,每个小正方体的棱长为2cm.
(1)画出该几何体的三视图(比例自选).
(2)求出该几何体的表面积.
9.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是 .
三、课堂达标
一、选择题(每小题4分,共32分)
1.由6个同样的立方体摆出从正面看是 的几何体,下面摆法正确的是( )
A. B.
C. D.
2.如图是大小相同的5个正方体搭成的几何体,其左视图是( )
A. B.
C. D.
3.下列四个几何体中,左视图为圆的是( )
A. B.
C. D.
4.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,这种连接方式不但可以承受较大的荷载,而且允许产生一定的变形.右图是某种榫卯构件的示意图,其中榫的俯视图是( )
A. B.
C. D.
5.如图的几何体是由10个相同的小正方体搭成的,若移走下列中的一块小正方体后,该几何体的主视图会发生改变,则可能移走的是( )
A.① B.② C.③ D.④
6.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不相同的几何体是( )
A.①② B.②③ C.②④ D.③④
7.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A.108cm3 B.100 cm3 C.92cm3 D.84cm3
8.某三棱锥的三视图如图所示,该三棱锥的体积是( )
A. B.4 C.2 D.
二、填空题(每小题4分,共20分)
9.桌上放着一个圆锥和长方体的组合体(如图①),图②③④是它的三视图,请在下面横线上写出三个视图的名称.
. . .
10.由个大小相同的小立方块搭成的几何体的左视图和俯视图如图所示,则的值为 .
11.一个长方体的三种视图如图所示,若其俯视图为正方形,则这个长方体的体积为 .
12.下图是由若干个相同的小正方体组合而成的一个几何体的三视图,则组成这个几何体的小正方体个数是 .
13.如图,是一几何体的三视图,根据图中数据,这个几何体的侧面积是 .
三、解答题(每小题8分,共48分)
14.按如图所标的主视方向填写下列几何体的三视图的名称.
圆柱 圆锥 球
主视图
俯视图
左视图
15.如图是一个直三棱柱的立体图和三视图,根据立体图上的尺寸,求:
(1)三视图中AB的长.
(2)左视图的面积.
16.已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.
17.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所示尺寸(单位:mm),计算出这个立体图形的表面积.
18.已知一个几何体的三视图如图所示,则该几何体的体积为多少?
19.分别画出如图所示几何体的三视图,并求几何体的表面积和体积.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
29.2 三视图
学习目标:
1.会从投影的角度理解视图的概念;
2.会画简单几何体的三视图;
3.会利用三视图计算立体图形的侧面积和表面积
4.通过观察探究等活动知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系.
老师告诉你
1.由三视图想象立体图形,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面、左面,然后再综合起来考虑整体图形。
2.由物画图与由图想物是相互联系的两类问题,前者是“分解”,后者是“综合”,体会由三视图想象立体图形,感受“综合”思考过程.
一、知识点拨
知识点1 、 三视图概念及被观察物体三视图之间的关系:
三视图的概念
视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水 平面,右边的面叫做侧面.
(3)三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
被观察物体三视图之间的关系
(1)位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
(2)大小关系
1.主视图和俯视图的长要相等;
2.主视图和左视图的高要相等;
3.左视图和俯视图的宽要相等.
口诀:主俯长对正、主左高平齐、俯左宽相等.
【新知导学】
例1-1.在下面的四个几何体中,三视图相同的是( )
A. B. C. D.
【答案】A
【知识点】简单几何体的三视图
【解析】【解答】解:A、球的主视图,俯视图,左视图都是圆,符合题意;
B、圆锥的主视图和左视图都是三角形,俯视图是圆,不符合题意;
C、三棱柱的主视图和左视图都是长方形,俯视图是三角形,不符合题意;
D、圆柱的主视图和左视图都是长方形,俯视图是圆,不符合题意.
故答案为:A.
【分析】主视图,就是从前向后看得到的正投影;左视图,就是从左向右看得到的正投影;俯视图,就是从上向下看得到的正投影,根据定义分别找出各个几何体的三个视图,即可逐一判断得出答案.
例1-2.下列几何体中,俯视图可能是三角形的是( )
A. B.
C. D.
【答案】B
【知识点】简单几何体的三视图
【解析】【解答】根据题意,俯视图可能是三角形的是
故选B.
【分析】根据俯视图的意义解答可.
【对应导练】
1. 如图蒙古包,其俯视图是( )
A. B.
C. D.
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:从上面看,俯视图为一个带圆心的圆,
即 .
故答案为:D.
【分析】根据俯视图是从上面看到的图形,即可得到答案.
2.如图所示的几何体是由一个圆柱和一个长方体组成的,它的左视图是( )
A. B.
C. D.
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:这个组合体的左视图为:
故答案为:D.
【分析】画出这个组合体的左视图即可求解.
知识点2 、 画三视图的具体方法:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图长对正;
3.在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
4.为表示圆柱、圆锥等的对称轴,规定在视图中用细点划线表示对称轴.
【注意】
画一个几何体的三视图,关键是把从正面、上方、左边三个方向观察时所得的视图画出来,所以,首先要注意观察时视线与观察面垂直,即观察到的平面图是该图的正投影;其二,要注意正确地用虚线表示看不到的轮廓线;其三,要充分发挥想象,多实践,多与同学交流探讨,多总结;最后,按三视图的位置和大小要求从整体上画出几何体的三视图.
【新知导学】
例2-1.在一个长方体上搁一个圆柱,所得几何体如图①所示,这个几何体的主视图、左视图如图②所示,请补画出它的俯视图.
【答案】解:如图所示.
【知识点】作图﹣三视图
【解析】【分析】根据简单组合体的三视图画法画出俯视图即可.
例2-2.如图,一个几何体由两个圆柱分别从纵横两个方向嵌入一个立方体中构成,圆柱的底面圆与立方体的底面内切.画出它的三视图(尺寸自选).
【答案】
【知识点】作图﹣三视图
【解析】【分析】根据简单组合体的三视图画法画出相应图形即可.
【对应导练】
1.中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的左视图为( )
A. B.
C. D.
【答案】B
【知识点】简单几何体的三视图
【解析】【解答】解:从左边观看立体图形可得:左视图为直角在左边的直角三角形,
故选:B.
【分析】左视图:从物体左面所看的平面图形,注意:看到的棱画实线,看不到的棱画虚线,据此进行解答即可.
2.一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱,它的俯视图如图所示.补画这个木模的主视图和左视图.
【答案】解:如图所示,
【知识点】作图﹣三视图
【解析】【分析】根据三视图的画法即可画出相应图形.
3.下面几何体的三视图是否完整 若不完整,请补全.
【答案】解:该几何体的三视图不完成,补全图形如下图.
【知识点】简单几何体的三视图;作图﹣三视图
【解析】【分析】 根据几何体的三视图画法画出图形,注意看得见部分的轮廓线画成实线,被遮挡部分的轮廓线画成虚线即可.
知识点3 、 已知三视图想象立体图形
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置以及各个方向的尺寸.
【新知导学】
例3-1.由若干个相同的小立方块搭成的几何体的主视图和俯视图如图所示.这样的几何体有多少种可能的搭法 分别画出它们的左视图.
【答案】解:这样的几何体有3种可能.左视图的示意图如图
【知识点】作图﹣三视图;由三视图判断小正方体的个数
【解析】【分析】根据主视图,俯视图,想像出几何体,再根据几体体画出左视图.
例3-2.一个几何体的主视图和俯视图如图所示,画出该几何体的左视图,并说出这个几何体的名称.
【答案】解:左视图
该几何体是直三棱柱.
【知识点】由三视图判断几何体;作图﹣三视图
【解析】【分析】根据俯视图三角形水平边上的高与主视图较短边为长与宽画出左视图.
【对应导练】
1.如图是某个几何体的三视图,则这个几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
【答案】D
【知识点】由三视图判断几何体
【解析】【解答】解:根据三视图的定义可得,该图形是三棱柱的三视图,
故答案为:D.
【分析】利用三棱柱三视图的特征分析求解即可.
2. 如图是某几何体的主视图、左视图和俯视图,则该几何体是( )
A.球 B.圆柱 C.圆锥 D.长方体
【答案】C
【知识点】由三视图判断几何体
【解析】【解答】解:∵主视图及左视图是三角形,
∴该几何体应该是椎体,
∵俯视图是圆形,
∴该几何体是圆锥.
故答案为:C.
【分析】由主视图及左视图可判断出是柱体还是椎体,再结合俯视图即可判断出是圆锥.
3.如图是一个几何体的三视图,则该几何体是( )
A. B.
C. D.
【答案】C
【知识点】由三视图判断几何体
【解析】【解答】解:A:主视图为:,不符合题意;
B:主视图为:,不符合题意;
C:主视图为:,符合题意;
D:主视图为:,不符合题意
故答案为:C
【分析】根据组合体的三视图,分别求出各项主视图即可求出答案.
4.一个几何体的三视图如图所示,这个几何体是 .
【答案】圆柱
【知识点】由三视图判断几何体
【解析】【解答】解:一个几何体的三视图中,主视图与左视图都是矩形,俯视图是圆,这个几何体是圆柱.
故答案为:圆柱.
【分析】根据所给的三视图,想像几何体.
知识点4 、 由三视图求立体图形的面积(体积)
1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
2)将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
3)最后根据已知数据,求出展开图的面积(体积).
【新知导学】
例4-1.下图是一个几何体的三视图.
(1)说出这个几何体的名称.
(2)请根据图中尺寸(单位:cm)求该几何体的全面积(结果保留π).
【答案】(1)解:该几何体为一个圆锥.
(2)解:由(1)可得:该几何题为圆锥,
底面圆半径r=12,高为6,
∴侧面母线长
∴
【知识点】圆锥的计算;由三视图判断几何体
【解析】【分析】(1)根据三视图的特征结合圆锥特征即可求出答案.
(2)根据勾股定理求出圆锥侧面母线长,再根据圆锥全面积公式即可求出答案.
例4-2.已知某几何体的三视图如下,其中俯视图为正方形,则这个长方体的底面边长为 .
【答案】2
【知识点】勾股定理;简单几何体的三视图
【解析】【解答】解:由主视图可得底面正方形对角线长为
设底面正方形边长为a
∴
解得:a=2
故答案为:2
【分析】根据主视图可得出底面正方形对角线,再根据勾股定理即可求出答案.
二、题型训练
1.画几何体的三视图
1.如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
A. B.
C. D.
【答案】C
【知识点】简单组合体的三视图;小正方体组合体的三视图
【解析】【解答】解:俯视图为:.
故答案为:C.
【分析】俯视图是从几何体上面观察所得到的平面图形,据此判断.
2.如图所示的几何体的主视图是( )
A. B.
C. D.
【答案】A
【知识点】简单组合体的三视图
【解析】【解答】解:此题是一个圆柱与一个六棱柱的组合体,其主视图应该为:下面是一个矩形左右各加一竖实线,上面是一个矩形所以只有A选项符合题意.
故答案为:A.
【分析】主视图,就是从正面看得到的图形,看得见的轮廓线需要画成实线,看不见但又存在的轮廓线画成虚线,据此可的A选项是其主视图,B选项是其左视图,C选项是其俯视图.
3.如图所示的几何体的俯视图是( )
A. B. C. D.
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:从上面看该几何体,选项D的图形符合题意,
故答案为:D.
【分析】俯视图是从几何体上面观察所得到的平面图形,据此判断.
由三视图确定几何体
4.如图是由几个小立方块所搭成的几何体从上面所看到的,小正方形中的数字表示在该方块的个数,则从左边看到的这个几何体的形状图为( )
A. B.
C. D.
【答案】B
【知识点】由三视图判断几何体
【解析】【解答】解:观察俯视图可知,这个几何体的左视图由3列小正方形组成,最左列只有一个正方形,中间列有3个,最右边一列有2个,
故答案为:B.
【分析】本题考查的是几何体的三视图,由条件中的俯视图可以判断出几何体的形状,再以此推断出几何体的左视图.
5.一个几何体由若干个大小相同的小立方块搭成,如图分别是它的主视图和俯视图,若该几何体所用小立方块的个数为个,则的最小值为( )
A.9 B.11 C.12 D.13
【答案】A
【知识点】由三视图判断几何体
【解析】【解答】解:根据主视图、俯视图可得:当小立方块个数最少时,在俯视图的相应位置上所摆放的个数如下:
故n的最小值为1+1+1+1+2+3=9.
故答案为:9.
【分析】根据主视图、俯视图可得:当小立方块个数最少时,每层摆放的个数,然后相加即可.
3.由三视图确定几何体的表面积
6.如图是一几何体的三视图,请选择恰当的比例,画出其表面展开图,并计算它的侧面积与全面积.
【答案】表面展开图如图所示
它的侧面积是(1.5+2+2.5)×3=18(cm2);
它的全面积是18+×1.5×2×2=21(cm2)
【知识点】几何体的表面积;几何体的展开图;由三视图判断几何体
【解析】【分析】根据三视图可知,这个几何体是三棱柱,据此画出展开图,求出侧面积,全面积即可.
7.如图是某几何体的三视图,则该几何体的体积是( )
A.. B.. C.. D..
【答案】C
【知识点】简单组合体的三视图
【解析】【解答】解:根据题意可知该几何体是六棱柱,且底面是正六边形,
将正六边形分成6个全等的等边三角形,过点A作AD⊥BC于点D,如图,
由题意得AB=BC=5,BD=2.5,
∴根据勾股定理得,
∴,
∴正六边形得面积为,
∵由题意得六棱柱的高为2,
∴该几何体六棱柱的体积是.
故答案为:C.
【分析】先根据题意得到该几何体是六棱柱,且底面是正六边形,根据棱柱的体积公式是V=Sh(S是底面积,h是棱柱的高),可先求出底面积,把它分成6个全等的等边三角形去求,利用勾股定理求出等边三角形的高即可求出底面积,最后再代入体积公式即可求出答案.
8.由7个完全相同的小立方体搭成的几何体如下,每个小正方体的棱长为2cm.
(1)画出该几何体的三视图(比例自选).
(2)求出该几何体的表面积.
【答案】(1)解:画三视图如下.
(2)解:S表面=(5+3+5)×2×2×2+2×2×2=112(cm2).
【知识点】作图﹣三视图;小正方体组合体的表面积
【解析】【分析】(1)直接根据立体图形画出三视图即可;
(2)由立体图形可知,正面有5个面,后面有5个面,上面有5个面,底面有5个面,左面有3个面,右面有3个面,中间内侧有2个面,即(5+3+5)×2×2×2+2×2×2=112(cm2).
9.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是 .
【答案】12π
【知识点】圆锥的计算;由三视图判断几何体;圆柱的侧面积和表面积
【解析】【解答】解:由三视图可得该结合体上面是圆锥,下面是圆柱,
根据三视图中的数据可得圆锥的母线长为=2,
∴该整流罩的侧面积为π×2.4×4+π×(2.4÷2)×2=12π.
故答案为:12π.
【分析】由三视图可得该结合体上面是圆锥,下面是圆柱,根据三视图中的数据求出圆锥的母线长,然后根据圆柱、圆锥的侧面积公式进行计算.
三、课堂达标
一、选择题(每小题4分,共32分)
1.由6个同样的立方体摆出从正面看是 的几何体,下面摆法正确的是( )
A. B.
C. D.
【答案】B
【知识点】简单几何体的三视图
【解析】【解答】解:A、主视图得到两行两列,故A不符合题意
B、主视图是,故B符合题意
C、主视图是两行三列,且第一二列都是两个,故C不符合题意
D、主视图是两行四列,故D不符合题意
故答案为:B.
【分析】从一个几何体正面投射得到的视图叫几何体的主视图.
2.如图是大小相同的5个正方体搭成的几何体,其左视图是( )
A. B.
C. D.
【答案】A
【知识点】简单组合体的三视图
【解析】【解答】解:根据立体图可知该左视图是底层有2个小正方形,第二层左边有1个小正方形.
故选:A.
【分析】从左边观察即可判断.
3.下列四个几何体中,左视图为圆的是( )
A. B.
C. D.
【答案】A
【知识点】简单几何体的三视图
【解析】【解答】解:左视图为从左往右看得到的视图,
A.球的左视图是圆,
B.圆柱的左视图是长方形,
C.圆锥的左视图是等腰三角形,
D.圆台的左视图是等腰梯形,
故答案为:A.
【分析】根据三视图的定义求解即可。
4.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,这种连接方式不但可以承受较大的荷载,而且允许产生一定的变形.右图是某种榫卯构件的示意图,其中榫的俯视图是( )
A. B.
C. D.
【答案】D
【知识点】简单几何体的三视图
【解析】【解答】解:从上往下看立体图,可以得到俯视图的形状应该是四根实线夹着两根虚线的长方形,如图所示:
故选:D.
【分析】利用几何体俯视图的定义(从上面观察物体所得到的视图是俯视图)分析求解即可.
5.如图的几何体是由10个相同的小正方体搭成的,若移走下列中的一块小正方体后,该几何体的主视图会发生改变,则可能移走的是( )
A.① B.② C.③ D.④
【答案】D
【知识点】简单组合体的三视图
【解析】【解答】解:由几何体的搭建可知,若移走下列中的一块小正方体后,该几何体的主视图会发生改变,则可能移走的小正方体是④.
故答案为:D.
【分析】根据主视图是从正面看到的图像即可判断.
6.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不相同的几何体是( )
A.①② B.②③ C.②④ D.③④
【答案】B
【知识点】简单几何体的三视图
【解析】【分析】先分别分析四种几何体的三种视图,再找出有两个相同而另一个不同的几何体.
【解答】①因为正方体的三个视图都相同,都是正方形,不符合条件;
②圆柱的主视图与左视图都是长方形,俯视图是圆,符合条件;
③圆锥的主视图与左视图都是三角形,俯视图是圆中间还有一点,符合条件;
④球的三个视图都相同,都是圆,不符合条件.
故符合条件的是:②③.
故选:B.
【点评】此题主要考查了学生的观察能力和对几何体三种视图的空间想象能力
7.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A.108cm3 B.100 cm3 C.92cm3 D.84cm3
【答案】B
【知识点】由三视图判断几何体
【解析】【解答】解:由三视图可知:该几何体是一个棱长分别为6cm,6cm,3cm的长方体截去一个三条侧棱长分别为4cm,4cm,3cm的一个三棱锥(长方体的一个角)后的图形,如图所示.
∴该几何体的体积V=6×6×3-
=100(cm3).
故答案为B。
【分析】从三视图,若不看每个图中斜的实线,我们会发现该几何体是一个长方体;根据斜线的位置可以确定该几何体是由一个长方体截掉一个棱锥所得到的。由三视图得到长方体的长、宽、高,以及三棱锥的底面三角形的底与高,和三棱锥的高。
8.某三棱锥的三视图如图所示,该三棱锥的体积是( )
A. B.4 C.2 D.
【答案】B
【知识点】由三视图判断几何体
【解析】【解答】解:由主视图和俯视图,底面三角形一条边长为4,
由左视图可得底面三角形边长为4的边对应的高长为3,且三棱锥的高是2,
则三棱锥的体积是
故答案为:B。
【分析】由三棱锥的体积公式,则需要求出底面的面积及三棱锥的高;由主视图和俯视图,底面三角形一条边长为4;由左视图可得底面三角形边长为4的边对应的高长为3,且三棱锥的高是2,从而代入公式计算即可。
二、填空题(每小题4分,共20分)
9.桌上放着一个圆锥和长方体的组合体(如图①),图②③④是它的三视图,请在下面横线上写出三个视图的名称.
. . .
【答案】俯视图;左视图;主视图
【知识点】简单组合体的三视图
【解析】【解答】解: 根据题意得,图 ② 是该几何体的俯视图;图 ③是该几何体的左视图;图 ④ 是该几何体的主视图.
故答案为:俯视图;左视图;主视图.
【分析】根据三视图的概念,观察几何体后即可得出答案.
10.由个大小相同的小立方块搭成的几何体的左视图和俯视图如图所示,则的值为 .
【答案】6或7
【知识点】简单组合体的三视图;由三视图判断小正方体的个数
【解析】【解答】解:根据俯视图有5个正方形,可知几何体至少有5个小立方体,再根据左视图,可知几何体还可能有1或2个小立方体,故n的值为6或7.
故答案为:6或7.
【分析】先根据俯视图,得出n至少有几个,再根据左视图可得还可能有几个,再求n.
11.一个长方体的三种视图如图所示,若其俯视图为正方形,则这个长方体的体积为 .
【答案】144
【知识点】简单几何体的三视图;由三视图判断几何体
【解析】【解答】由图形可得长方体体积为,
【分析】根据对角线为6cm,俯视图是一个长方形,则地面面积为(cm2),再根据长方体体积公式计算即可.
12.下图是由若干个相同的小正方体组合而成的一个几何体的三视图,则组成这个几何体的小正方体个数是 .
【答案】5
【知识点】由三视图判断几何体
【解析】【解答】解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,
第二有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
故答案为:5.
【分析】 根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
13.如图,是一几何体的三视图,根据图中数据,这个几何体的侧面积是 .
【答案】
【知识点】圆锥的计算;由三视图判断几何体
【解析】【解答】解:由三视图可知,原几何体为圆锥,
∵圆锥的底面半径为: ,圆锥的高为: ,
∴圆锥的母线长为: ,
∴ ;
∴这个几何体的侧面积是 ;
故答案为: .
【分析】根据三视图的定义判断出该物体为圆锥,再利用圆锥的侧面积计算即可。
三、解答题(每小题8分,共48分)
14.按如图所标的主视方向填写下列几何体的三视图的名称.
圆柱 圆锥 球
主视图
俯视图
左视图
【答案】
圆柱 圆锥 球
主视图 矩形 等腰三角形 圆
俯视图 圆 圆和圆心 圆
左视图 矩形 等腰三角形 圆
【知识点】简单几何体的三视图
【解析】【分析】根据圆柱图、圆锥、球体的三视图进行填空即可解答.
15.如图是一个直三棱柱的立体图和三视图,根据立体图上的尺寸,求:
(1)三视图中AB的长.
(2)左视图的面积.
【答案】(1)解:如图,根据题意可知AC=AD=5,DC=6,过点D作DB⊥AC于点B,
设AB=x,则BC=5-x,
在与中,根据勾股定理得AD2-AB2=CD2-CB2,
∴52-x2=62-(5-x)2,
∴,即三视图中AB的长为;
(2)解:由(1)有,
∴在中,,
∴左视图面积为.
【知识点】简单几何体的三视图
【解析】【分析】(1)利用俯视图, 如图所示,AC=AD=5,DC=6,过点D作DB⊥AC于点B,设AB=x,根据勾股定理构建方程求解即可;
(2)左视图是一个长方形,根据题意得两边长的长度,再利用面积公式求解即可.
16.已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.
【答案】解:如图所示:根据三视图可以得出:此物体是:三棱柱表面积:S表=6×8+4×6+4×8+4×10=144(cm2);体积:V=×6×8×4=96(cm3).
【知识点】由三视图判断几何体
【解析】【分析】根据三视图得出几何体的各边长度,进而得出几何体的表面积和体积即可.
17.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所示尺寸(单位:mm),计算出这个立体图形的表面积.
【答案】解:根据三视图可得:上面的长方体长4mm,高4mm,宽2mm,
下面的长方体长8mm,宽6mm,高2mm,
∴立体图形的表面积是:4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2).
故答案为200 mm2.
【知识点】由三视图判断几何体
【解析】【分析】根据三视图可知立体图形下面的长方体的长、宽、高分别 8mm,6mm,2mm,上面的长、宽、高分别 4mm,2mm,4mm。由此计算这个立体图形的表面积即可。
18.已知一个几何体的三视图如图所示,则该几何体的体积为多少?
【答案】解:由三视图可其看成为两个长方体上、下叠放而成。
下面的长方体的长、宽、高分别为5、5、4;
上面的长方体的长、宽、高分别为5、4、1;
则该组合体的体积是5×5×4+5×4×1=120.
【知识点】由三视图判断几何体
【解析】【分析】由三视图将该几何看成是由两个长方体靠右对齐叠放而成;由标出的数据确定每个长方体的长宽高,从而计算两个长方体的体积和。
19.分别画出如图所示几何体的三视图,并求几何体的表面积和体积.
【答案】解:①
由勾股定理易得主视图中等腰三角形的腰长为5cm,
表面积为:6×2×2+8×2×2+2×6×4÷2+2×5×8+6×8=208cm2;
体积为:(6×2+6×4÷2)×8=192cm3;
②
表面积为:9×4.5×2+4.5×9×2+(4.5×4.5﹣1.5×3)×2+3×9×2=247.5cm2;
体积为:(4.5×4.5﹣1.5×3)×9=141.75cm3;
③
表面积为:15×5×2+10×15+(2×10×5﹣π×32)+ π(10﹣2﹣2)×15=(460+36π)cm2;
体积为:(10×5﹣ π×32)×15=(750﹣67.5π)cm3.
【知识点】作图﹣三视图
【解析】【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;计算表面积找到所有面的和相加即可;所给几何体的体积均为相应的底面积乘高,把相关数值代入即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
