人教版九年级数学下名师点拨与训练第28章 锐角三角函数小结与复习
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第28章 锐角三角函数小结与复习 |
|
|
| 格式 | doc | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
小结与复习
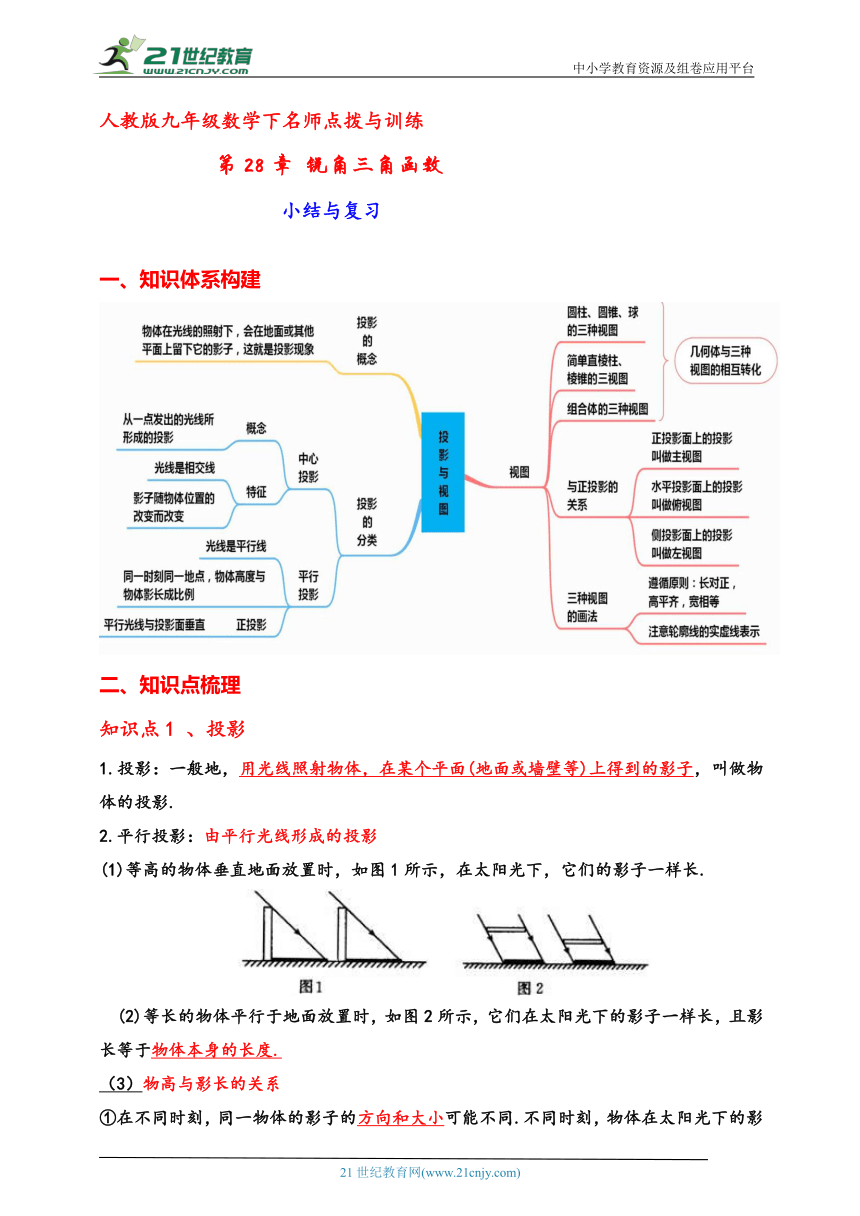
知识体系构建
知识点梳理
知识点1 、投影
1.投影:一般地,用光线照射物体,在某个平面(地面或墙壁等)上得到的影子,叫做物体的投影.
2.平行投影:由平行光线形成的投影
(1)等高的物体垂直地面放置时,如图1所示,在太阳光下,它们的影子一样长.
(2)等长的物体平行于地面放置时,如图2所示,它们在太阳光下的影子一样长,且影长等于物体本身的长度.
(3)物高与影长的关系
①在不同时刻,同一物体的影子的方向和大小可能不同.不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚,物体影子的指向是:西→西北→北→东北→东,影长也是由长变短再变长.
②在同一时刻,不同物体的物高与影长成正比例.
即:.
利用上面的关系式可以计算高大物体的高度,比如旗杆的高度等.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
3.中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影.这个“点”就是中心,相当于物理上学习的“点光源”
(1)等高的物体垂直地面放置时,如图1所示,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
(2)等长的物体平行于地面放置时,如图2所示.一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
在中心投影的情况下,还有这样一个重要结论:点光源、物体边缘上的点以及它在影子上的对应点在同一条直线上,根据其中两个点,就可以求出第三个点的位置.
知识点2 、平行投影与中心投影的区别与联系
1.联系:
(1)中心投影、平行投影都是研究物体投影的一种,只不过平行投影是在平行光线下所形成的投影,通常的平行光线有太阳光线、月光等,而中心投影是从一点发出的光线所形成的投影,通常状况下,灯泡的光线、手电筒的光线等都可看成是从某一点发射出来的光线.
(2)在平行投影中,同一时刻改变物体的方向和位置,其投影也跟着发生变化;在中心投影中,同一灯光下,改变物体的位置和方向,其投影也跟着发生变化.在中心投影中,固定物体的位置和方向,改变灯光的位置,物体投影的方向和位置也要发生变化.
2.区别:
(1)太阳光线是平行的,故太阳光下的影子长度都与物体高度成比例;灯光是发散的,灯光下的影子与物体高度不一定成比例.
(2)同一时刻,太阳光下影子的方向总是在同一方向,而灯光下的影子可能在同一方向,也可能在不同方向.
知识点3 、三视图
1 .正投影
正投影的定义:
如图所示,图(1)中的投影线集中于一点,形成中心投影;图(2)(3)中,投影线互相平行,形成平行投影;图(2)中,投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
(1)线段的正投影分为三种情况.如图所示.
①线段AB平行于投影面P时,它的正投影是线段A1B1,与线段AB的长相等;
②线段AB倾斜于投影面P时,它的正投影是线段A2B2,长小于线段AB的长;
③线段AB垂直于投影面P时,它的正投影是一个点.
(2)平面图形正投影也分三种情况,如图所示.
①当平面图形平行于投影面Q时,它的正投影与这个平面图形的形状、大小完全相同,即正投影与这个平面图形全等;
②当平面图形倾斜于投影面Q时,平面图形的正投影与这个平面图形的形状、大小发生变化,即会缩小,是类似图形但不一定相似.
③当平面图形垂直于投影面Q时,它的正投影是直线或直线的一部分.
(3)立体图形的正投影.
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最大截面全等.
2 .三视图
(1).三视图的概念
①视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
②正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水平面,右边的面叫做侧面.
③三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
(2).三视图之间的关系
①位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
②大小关系
三视图之间的大小是相互联系的,遵循主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等的原则.如图(2)所示.
知识点4 、画几何体的三视图
画图方法:
画一个几何体的三视图时,要从三个方面观察几何体,具体画法如下:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
几何体上被其他部分遮挡而看不见的部分的轮廓线应画成虚线.
知识点5、由三视图想象几何体的形状
由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象主体图的前面、上面和左侧面,然后综合起来考虑整体图形.
三、高频考点
考点1 平行投影
【例1-1】.在平行投影下,矩形的投影不可能是( )
A. B. C. D.
【例1-2】.下列说法正确的是( )
A.物体在阳光下的投影只与物体的高度有关
B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.
C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.
D.物体在阳光照射下,影子的长度和方向都是固定不变的.
【变式1-1】.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③—④—①—② B.②—①—④—③
C.④—①—②—③ D.④—①—③—②
【变式1-2】.日晷是我国古代利用日影测定时刻的一种计时仪器,它由“晷面”和“晷针”组成,古人常用的日晷有水平式日晷(图1)和赤道式日晷(图2).其中水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度且“晷面”与地面平行;赤道式日晷的“晷面”与赤道面平行当太阳光照在日晷上时,晷针的影子就会投向晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以此来显示时刻.此外,水平式日晷的“晷面”刻度不均匀,赤道式日晷的“晷面”刻度则是均匀的.
(1)如图1,当水平式日晷放在纬度为(即)位置时,晷针与晷面的夹角为__________°.
(2)如图3,将两种日晷的“晷针”重合,n小时后,两种日晷对应的时刻一致,即两种晷“晷针”的影子所在的直线相交于点.此时,与满足的关系式__________.
【变式1-3】.如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是_________投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
考点2 中心投影
【例2-1】.下列哪种光线形成的投影不是中心投影( )
A.台灯 B.太阳 C.手电筒 D.路灯
【例2-2】.如图,白炽灯正下方有一个乒乓球,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子( )
A.越来越大 B.越来越小 C.先变大后变小 D.先变小后变大
【变式2--1】.下列选项能正确反映小亮和小美在同一盏路灯的两侧站立时影子情况的是( )
A. B.
C. D.
【变式2-2】.广场上有一个高20米的路灯,一天晚上,身高1.65米的小刚路过这里,发现自己的影长是身高的2倍,这时小刚离路灯的距离是_________米.
【变式2-3】.在一直线上有几根竹竿.它们在同一灯光下的影子如图所示(图中的粗线段).
(1)根据灯光下的影子确定光源的位置;
(2)画出竹竿AB的影子(用线段表示);
(3)画出影子为CD的竹竿(用线段表示).
考点3 视点、视角、盲区
【例3-1】.如图,区域为驾驶员的盲区,驾驶员视线与地面的夹角,视线与地面的夹角,点为视线与车窗底端的交点,.若A点到B点的距离,则盲区中的长度是( )
(参考数据:)
A.2.6m B.2.8m C.3.4m D.4.5m
【变式3-1】.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A. B.
C. D.四边形
【变式3-2】.最佳视点
如图1,设墙壁上的展品最高处点P距底面a米,最低处的点Q距底面b米,站在何处观赏最理想?所谓观赏理想是指看展品的视角最大,问题转化为在水平视线EF上求使视角最大的点.
如图2,当过P、Q、E三点的圆与过点E的水平线相切于点E时,视角最大,站在此处观赏最理想,小明同学想这是为什么呢?他在过点E的水平线上任取异于点E的点,连接交于点F,连接,…
任务一:请按照小明的思路,说明在点E时视角最大;
任务二:若,,观察者的眼睛距地面的距离为1.5米,最大视角为,求观察者应该站在距离多远的地方最理想(结果精确到0.01米,参考数据).
考点4 判断几何体的三视图
【例4-1】.篆刻是中华传统艺术之一,雕刻印章是篆刻基本功.如图是一块雕刻印章的材料,其俯视图为( )
A. B. C. D.
【例4-2】.下列几何体都是由相同的小立方体搭成的,几何体的左视图与其他三个不同的是( )
A. B. C. D.
【变式4-1】.如图,是由几个大小完全一样的小正方体搭成的几何体,该几何体从左面看的形状图是( )
A. B.
C. D.
【变式4-2】..如图是平面切割正方体得到的几何体,该几何体的主视图是( )
A. B. C. D.
【变式4-3】..榫卯是古代中国建筑、家具等的主要结构方式,如图是某个部件“卯”的实物图,它的左视图是( )
A. B. C. D.
考点5 画几何体的三视图
【例5-1】.请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
【例5-2】.一个零件是由长为、高和宽都为的长方体与直径为、高度为的半圆柱组成几何体后,又切去直径为的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.
【变式5-1】.从大正方体中挖去一个小正方体,得到一个如图所示的零件,画出该零件的三视图.
【变式5-2】.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
A. B.
C. D.
【变式5-3】.用五个相同的正方体搭成如图所示的立体图形,则该立体图形的主视图是( )
A. B. C. D.
考点6由三视图确定几何体
【例6-1】.如图是一个立体图形的三视图,该立体图形是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
【例6-2】.如图为某几何体的三种视图,这个几何体可以是( )
A. B. C. D.
【变式6-1】.根据三视图,描述这个物体的形状.
变式6-2】.根据三视图,描述这个物体的形状.
【变式6-3】.由5个相同的小正方体搭成的物体的俯视图如图所示,这个物体有几种搭法?
【变式6-4】.根据下列三视图想象物体原形,并分别画出物体的实物图.
考点7 由三视图求几何体的表面积
【例7-1】.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称:______;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
【例7-2】.根据下列三视图,求它们表示的几何体的体积(图中标有尺寸).
【变式7-1】.图(1)是由两个长方体组成的立体图形,图(2)中的长方体是图(1)中的两个长方体的另一种摆放形式,图①②③是从不同的方向看图(1)所得的平面图形.
(1)填空:图①是从___________面看得到的平面图形,图②是从___________面看得到的平面图形,图③是从___________面看得到的平面图形,
(2)请根据各图中所给的信息(单位:cm),计算出图(1)中上面的小长方体的体积.
【变式7-2】.已知某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C. D.
【变式7-3】..如图,是一个底面为等边三角形的正三棱柱和它的主视图及俯视图,则它的左视图的面积是( )
A. B.8 C. D.16
【变式7-4】..如图,计算所给三视图表示的几何体的体积是_____.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
小结与复习
知识体系构建
二、知识点梳理
知识点1 、投影
1.投影:一般地,用光线照射物体,在某个平面(地面或墙壁等)上得到的影子,叫做物体的投影.
2.平行投影:由平行光线形成的投影
(1)等高的物体垂直地面放置时,如图1所示,在太阳光下,它们的影子一样长.
(2)等长的物体平行于地面放置时,如图2所示,它们在太阳光下的影子一样长,且影长等于物体本身的长度.
(3)物高与影长的关系
①在不同时刻,同一物体的影子的方向和大小可能不同.不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚,物体影子的指向是:西→西北→北→东北→东,影长也是由长变短再变长.
②在同一时刻,不同物体的物高与影长成正比例.
即:.
利用上面的关系式可以计算高大物体的高度,比如旗杆的高度等.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
3.中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影.这个“点”就是中心,相当于物理上学习的“点光源”
(1)等高的物体垂直地面放置时,如图1所示,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
(2)等长的物体平行于地面放置时,如图2所示.一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
在中心投影的情况下,还有这样一个重要结论:点光源、物体边缘上的点以及它在影子上的对应点在同一条直线上,根据其中两个点,就可以求出第三个点的位置.
知识点2 、平行投影与中心投影的区别与联系
1.联系:
(1)中心投影、平行投影都是研究物体投影的一种,只不过平行投影是在平行光线下所形成的投影,通常的平行光线有太阳光线、月光等,而中心投影是从一点发出的光线所形成的投影,通常状况下,灯泡的光线、手电筒的光线等都可看成是从某一点发射出来的光线.
(2)在平行投影中,同一时刻改变物体的方向和位置,其投影也跟着发生变化;在中心投影中,同一灯光下,改变物体的位置和方向,其投影也跟着发生变化.在中心投影中,固定物体的位置和方向,改变灯光的位置,物体投影的方向和位置也要发生变化.
2.区别:
(1)太阳光线是平行的,故太阳光下的影子长度都与物体高度成比例;灯光是发散的,灯光下的影子与物体高度不一定成比例.
(2)同一时刻,太阳光下影子的方向总是在同一方向,而灯光下的影子可能在同一方向,也可能在不同方向.
知识点3 、三视图
1 .正投影
正投影的定义:
如图所示,图(1)中的投影线集中于一点,形成中心投影;图(2)(3)中,投影线互相平行,形成平行投影;图(2)中,投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
(1)线段的正投影分为三种情况.如图所示.
①线段AB平行于投影面P时,它的正投影是线段A1B1,与线段AB的长相等;
②线段AB倾斜于投影面P时,它的正投影是线段A2B2,长小于线段AB的长;
③线段AB垂直于投影面P时,它的正投影是一个点.
(2)平面图形正投影也分三种情况,如图所示.
①当平面图形平行于投影面Q时,它的正投影与这个平面图形的形状、大小完全相同,即正投影与这个平面图形全等;
②当平面图形倾斜于投影面Q时,平面图形的正投影与这个平面图形的形状、大小发生变化,即会缩小,是类似图形但不一定相似.
③当平面图形垂直于投影面Q时,它的正投影是直线或直线的一部分.
(3)立体图形的正投影.
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最大截面全等.
2 .三视图
(1).三视图的概念
①视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
②正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水平面,右边的面叫做侧面.
③三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
(2).三视图之间的关系
①位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
②大小关系
三视图之间的大小是相互联系的,遵循主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等的原则.如图(2)所示.
知识点4 、画几何体的三视图
画图方法:
画一个几何体的三视图时,要从三个方面观察几何体,具体画法如下:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
几何体上被其他部分遮挡而看不见的部分的轮廓线应画成虚线.
知识点5、由三视图想象几何体的形状
由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象主体图的前面、上面和左侧面,然后综合起来考虑整体图形.
三、高频考点
考点1 平行投影
【例1-1】.在平行投影下,矩形的投影不可能是( )
A. B. C. D.
答案:A
解析:因为矩形的投影是在平行投影下,所以对边平行或重合成一条线段,故选项A错误.故选A.
【例1-2】.下列说法正确的是( )
A.物体在阳光下的投影只与物体的高度有关
B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.
C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.
D.物体在阳光照射下,影子的长度和方向都是固定不变的.
答案:C
解析:A、物体在阳光下的投影不只与物体的高度有关,还与时刻有关,错误;
B、小明的个子比小亮高,在不同的时间,小明的影子可能比小亮的影子短,错误;
C、不同时刻物体在太阳光下的影子的大小在变,方向也在改变,正确;
D、不同时刻物体在太阳光下的影子的大小在变,方向也在改变,错误.
故选:C.
【变式1-1】.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③—④—①—② B.②—①—④—③
C.④—①—②—③ D.④—①—③—②
答案:B
解析:众所周知,影子方向的变化是上午时朝向西边,中午时朝向北边,下午时朝向东边;
影子长短的变化是由长变短再变长,结合方向和长短的变化即可得出答案
故选:B.
【变式1-2】.日晷是我国古代利用日影测定时刻的一种计时仪器,它由“晷面”和“晷针”组成,古人常用的日晷有水平式日晷(图1)和赤道式日晷(图2).其中水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度且“晷面”与地面平行;赤道式日晷的“晷面”与赤道面平行当太阳光照在日晷上时,晷针的影子就会投向晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以此来显示时刻.此外,水平式日晷的“晷面”刻度不均匀,赤道式日晷的“晷面”刻度则是均匀的.
(1)如图1,当水平式日晷放在纬度为(即)位置时,晷针与晷面的夹角为__________°.
(2)如图3,将两种日晷的“晷针”重合,n小时后,两种日晷对应的时刻一致,即两种晷“晷针”的影子所在的直线相交于点.此时,与满足的关系式__________.
答案:(1)
(2)
解析:(1)水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度,
当水平式日晷放在纬度为(即)位置时,晷针与晷面的夹角为;
故答案为:;
(2)过点作于点E,如图所示:
则,
,
根据题意可知,赤道日晷的晷面与晷针垂直,
,
,
,
,
根据平行投影可知,当12点时,点在水平方向的投影为点E,经过n小时后,的投影在上,因此,
,
.
故答案为:.
【变式1-3】.如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是_________投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
答案:(1)平行
(2)7米
解析:(1)平行
(2)如图,过点E作于点M,过点G作于点N.
则米,米,米,米,(米).由平行投影的性质可知,即,米,即电线杆的高度为7米.
考点2 中心投影
【例2-1】.下列哪种光线形成的投影不是中心投影( )
A.台灯 B.太阳 C.手电筒 D.路灯
答案:B
解析:中心投影的光源为蜡烛、台灯、路灯这样的光,而平行投影的光源为太阳光与月光,由此可得形成的投影不是中心投影的是太阳,
故答案选择:B.
【例2-2】.如图,白炽灯正下方有一个乒乓球,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子( )
A.越来越大 B.越来越小 C.先变大后变小 D.先变小后变大
答案:B
解析:根据中心投影的特点,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子越来越小,
故选:B.
【变式2--1】.下列选项能正确反映小亮和小美在同一盏路灯的两侧站立时影子情况的是( )
A. B.
C. D.
答案:D
解析:小亮和小美在同一盏路灯的两侧站立时影子情况应如图所示:
故选D.
【变式2-2】.广场上有一个高20米的路灯,一天晚上,身高1.65米的小刚路过这里,发现自己的影长是身高的2倍,这时小刚离路灯的距离是_________米.
答案:36.7
解析:如图,由题意可得米,米,米,
,.设米,则米,,解得,小刚离路灯的距离是36.7米.
【变式2-3】.在一直线上有几根竹竿.它们在同一灯光下的影子如图所示(图中的粗线段).
(1)根据灯光下的影子确定光源的位置;
(2)画出竹竿AB的影子(用线段表示);
(3)画出影子为CD的竹竿(用线段表示).
答案:(1)见解析
(2)见解析
(3)见解析
解析:(1)如图,点P即为光源所在的位置.
(2)BE即为竹竿AB的影子.
(3)CF是影子为CD的竹竿.
考点3 视点、视角、盲区
【例3-1】.如图,区域为驾驶员的盲区,驾驶员视线与地面的夹角,视线与地面的夹角,点为视线与车窗底端的交点,.若A点到B点的距离,则盲区中的长度是( )
(参考数据:)
A.2.6m B.2.8m C.3.4m D.4.5m
答案:B
解析:本题考查解直角三角形的实际应用、矩形的判定和性质.
,
∴四边形为矩形.
由题意得,
.
,故选B.
【变式3-1】.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A. B.
C. D.四边形
答案:C
解析:由图知:在视点E的位置,看不到段,因此监视器的盲区在所在的区域,
故选:C.
【变式3-2】.最佳视点
如图1,设墙壁上的展品最高处点P距底面a米,最低处的点Q距底面b米,站在何处观赏最理想?所谓观赏理想是指看展品的视角最大,问题转化为在水平视线EF上求使视角最大的点.
如图2,当过P、Q、E三点的圆与过点E的水平线相切于点E时,视角最大,站在此处观赏最理想,小明同学想这是为什么呢?他在过点E的水平线上任取异于点E的点,连接交于点F,连接,…
任务一:请按照小明的思路,说明在点E时视角最大;
任务二:若,,观察者的眼睛距地面的距离为1.5米,最大视角为,求观察者应该站在距离多远的地方最理想(结果精确到0.01米,参考数据).
答案:任务一:见解析
任务二:观察者应该站在距离0.87米的地方最理想
解析:任务一:过点E的水平线上任取异于点E的点,连接交于点F,连接,
是的外角,
,
又与都是弧所对的圆周角,
,
,
在点E时视角最大.
任务二:,
,
又,
是等边三角形,.
如图2,连接,
是的切线,
,
,
,
,
又,
四边形是平行四边形,
,
.
由题意得,(米),
在中,(米).
答:观察者应该站在距离0.87米的地方最理想.
考点4 判断几何体的三视图
【例4-1】.篆刻是中华传统艺术之一,雕刻印章是篆刻基本功.如图是一块雕刻印章的材料,其俯视图为( )
A. B. C. D.
答案:D
解析:
【例4-2】.下列几何体都是由相同的小立方体搭成的,几何体的左视图与其他三个不同的是( )
A. B. C. D.
答案:D
解析:
【变式4-1】.如图,是由几个大小完全一样的小正方体搭成的几何体,该几何体从左面看的形状图是( )
A. B.
C. D.
答案:B
解析:从左边看,底层是两个小正方形,上层的左边是一个小正方形,
故选:B.
【变式4-2】..如图是平面切割正方体得到的几何体,该几何体的主视图是( )
A. B. C. D.
答案:B
解析:
【变式4-3】..榫卯是古代中国建筑、家具等的主要结构方式,如图是某个部件“卯”的实物图,它的左视图是( )
A. B. C. D.
答案:D
解析:从左边看到的平面图形是,
故选:D.
考点5 画几何体的三视图
【例5-1】.请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
答案:作图见解析
解析:从正面可以看到5个正方形,分3列,依次为3个,1个,1个,
所以从正面看的主视图为:
从左面可以看到4个正方形,分2列,依次为3个,1个,
所以从左面看的左视图为:
从上面可以看到4个正方形,分3列,依次为1个,2个,1个,
所以从上面看的俯视图为:
【例5-2】.一个零件是由长为、高和宽都为的长方体与直径为、高度为的半圆柱组成几何体后,又切去直径为的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.
答案:见解析
解析:三视图如图所示:
【变式5-1】.从大正方体中挖去一个小正方体,得到一个如图所示的零件,画出该零件的三视图.
答案:见解析
解析:如图:
【变式5-2】.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
A. B.
C. D.
答案:D
解析:从左边看,是一个矩形,矩形的中间有一条横向的虚线.
故选:D.
【变式5-3】.用五个相同的正方体搭成如图所示的立体图形,则该立体图形的主视图是( )
A. B. C. D.
答案:B
解析:解:根据主视图的意义可知,从正面看到四个正方形,
故选:B.
考点6由三视图确定几何体
【例6-1】.如图是一个立体图形的三视图,该立体图形是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
答案:D
解析:由主视图和左视图为三角形判断出是锥体,
根据俯视图是圆可判断出这个几何体应该是圆锥.
故选:D.
【例6-2】.如图为某几何体的三种视图,这个几何体可以是( )
A. B. C. D.
答案:A
解析:根据几何体的三视图,只有A选项符合题意;
故选:A.
【变式6-1】.根据三视图,描述这个物体的形状.
答案:这个物体是正六棱柱
解析:
变式6-2】.根据三视图,描述这个物体的形状.
答案:见解析
解析:该物体由六个小正方体构成,只有一排,最底层是三个小正方体,中间一层是两个小正方体,且这两个小正方体靠右放置,上面一层是一个小正方体,且靠右放置(如图所示).
【变式6-3】.由5个相同的小正方体搭成的物体的俯视图如图所示,这个物体有几种搭法?
答案:3种
解析:这个物体的搭法有3种,如图所示.
【变式6-4】.根据下列三视图想象物体原形,并分别画出物体的实物图.
答案:见解析
解析:图(1)、图(2)的物体的实物图如下所示:
考点7 由三视图求几何体的表面积
【例7-1】.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称:______;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
答案:(1)长方体或四棱柱
(2)
解析:(1)∵这个立方体的三视图都是长方形,
∴这个立方体是长方体或四棱柱.
(2)由三视图知该长方体的表面积:.
【例7-2】.根据下列三视图,求它们表示的几何体的体积(图中标有尺寸).
答案:(1)
(2)
解析:(1)由三视图知该几何体由两个圆柱组成,其中小圆柱在大圆柱的正上方.
,,
故.
(2)由三视图知该几何体的体积为一个长方体和一个半圆柱的体积和.
,
,
故.
【变式7-1】.图(1)是由两个长方体组成的立体图形,图(2)中的长方体是图(1)中的两个长方体的另一种摆放形式,图①②③是从不同的方向看图(1)所得的平面图形.
(1)填空:图①是从___________面看得到的平面图形,图②是从___________面看得到的平面图形,图③是从___________面看得到的平面图形,
(2)请根据各图中所给的信息(单位:cm),计算出图(1)中上面的小长方体的体积.
答案:(1)正或后;上;左或右
(2)
解析:(1)正或后;上;左或右
(2)由题图可得解得所以题图(1)中上面的小长方体的长、宽、高分别为,,,所以,即题图(1)中上面的小长方体的体积为.
【变式7-2】.已知某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C. D.
答案:D
解析:由三视图知该几何体是三棱柱与半圆柱的组合体,且三棱柱的底面是边长为2的正三角形,三棱柱的高为2;半圆柱的底面半径为1,高为2,该几何体的体积为
.故选D.
【变式7-3】..如图,是一个底面为等边三角形的正三棱柱和它的主视图及俯视图,则它的左视图的面积是( )
A. B.8 C. D.16
答案:C
解析:由三视图可知:底面等边三角形的边长为4,该几何体的高为4,
该几何体的左视图为长方形,
该长方形的长为该几何体的高4,宽为底面等边三角形的高,
底面等边三角形的高=,
它的左视图的面积是,
故选:C.
【变式7-4】..如图,计算所给三视图表示的几何体的体积是_____.
答案:
解析:由三视图可知几何体是下部为底面半径为4,高为8的圆柱,上部是底面半径为2,高为2的圆柱,
所以所求几何体的体积为:;
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
小结与复习
知识体系构建
知识点梳理
知识点1 、投影
1.投影:一般地,用光线照射物体,在某个平面(地面或墙壁等)上得到的影子,叫做物体的投影.
2.平行投影:由平行光线形成的投影
(1)等高的物体垂直地面放置时,如图1所示,在太阳光下,它们的影子一样长.
(2)等长的物体平行于地面放置时,如图2所示,它们在太阳光下的影子一样长,且影长等于物体本身的长度.
(3)物高与影长的关系
①在不同时刻,同一物体的影子的方向和大小可能不同.不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚,物体影子的指向是:西→西北→北→东北→东,影长也是由长变短再变长.
②在同一时刻,不同物体的物高与影长成正比例.
即:.
利用上面的关系式可以计算高大物体的高度,比如旗杆的高度等.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
3.中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影.这个“点”就是中心,相当于物理上学习的“点光源”
(1)等高的物体垂直地面放置时,如图1所示,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
(2)等长的物体平行于地面放置时,如图2所示.一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
在中心投影的情况下,还有这样一个重要结论:点光源、物体边缘上的点以及它在影子上的对应点在同一条直线上,根据其中两个点,就可以求出第三个点的位置.
知识点2 、平行投影与中心投影的区别与联系
1.联系:
(1)中心投影、平行投影都是研究物体投影的一种,只不过平行投影是在平行光线下所形成的投影,通常的平行光线有太阳光线、月光等,而中心投影是从一点发出的光线所形成的投影,通常状况下,灯泡的光线、手电筒的光线等都可看成是从某一点发射出来的光线.
(2)在平行投影中,同一时刻改变物体的方向和位置,其投影也跟着发生变化;在中心投影中,同一灯光下,改变物体的位置和方向,其投影也跟着发生变化.在中心投影中,固定物体的位置和方向,改变灯光的位置,物体投影的方向和位置也要发生变化.
2.区别:
(1)太阳光线是平行的,故太阳光下的影子长度都与物体高度成比例;灯光是发散的,灯光下的影子与物体高度不一定成比例.
(2)同一时刻,太阳光下影子的方向总是在同一方向,而灯光下的影子可能在同一方向,也可能在不同方向.
知识点3 、三视图
1 .正投影
正投影的定义:
如图所示,图(1)中的投影线集中于一点,形成中心投影;图(2)(3)中,投影线互相平行,形成平行投影;图(2)中,投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
(1)线段的正投影分为三种情况.如图所示.
①线段AB平行于投影面P时,它的正投影是线段A1B1,与线段AB的长相等;
②线段AB倾斜于投影面P时,它的正投影是线段A2B2,长小于线段AB的长;
③线段AB垂直于投影面P时,它的正投影是一个点.
(2)平面图形正投影也分三种情况,如图所示.
①当平面图形平行于投影面Q时,它的正投影与这个平面图形的形状、大小完全相同,即正投影与这个平面图形全等;
②当平面图形倾斜于投影面Q时,平面图形的正投影与这个平面图形的形状、大小发生变化,即会缩小,是类似图形但不一定相似.
③当平面图形垂直于投影面Q时,它的正投影是直线或直线的一部分.
(3)立体图形的正投影.
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最大截面全等.
2 .三视图
(1).三视图的概念
①视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
②正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水平面,右边的面叫做侧面.
③三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
(2).三视图之间的关系
①位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
②大小关系
三视图之间的大小是相互联系的,遵循主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等的原则.如图(2)所示.
知识点4 、画几何体的三视图
画图方法:
画一个几何体的三视图时,要从三个方面观察几何体,具体画法如下:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
几何体上被其他部分遮挡而看不见的部分的轮廓线应画成虚线.
知识点5、由三视图想象几何体的形状
由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象主体图的前面、上面和左侧面,然后综合起来考虑整体图形.
三、高频考点
考点1 平行投影
【例1-1】.在平行投影下,矩形的投影不可能是( )
A. B. C. D.
【例1-2】.下列说法正确的是( )
A.物体在阳光下的投影只与物体的高度有关
B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.
C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.
D.物体在阳光照射下,影子的长度和方向都是固定不变的.
【变式1-1】.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③—④—①—② B.②—①—④—③
C.④—①—②—③ D.④—①—③—②
【变式1-2】.日晷是我国古代利用日影测定时刻的一种计时仪器,它由“晷面”和“晷针”组成,古人常用的日晷有水平式日晷(图1)和赤道式日晷(图2).其中水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度且“晷面”与地面平行;赤道式日晷的“晷面”与赤道面平行当太阳光照在日晷上时,晷针的影子就会投向晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以此来显示时刻.此外,水平式日晷的“晷面”刻度不均匀,赤道式日晷的“晷面”刻度则是均匀的.
(1)如图1,当水平式日晷放在纬度为(即)位置时,晷针与晷面的夹角为__________°.
(2)如图3,将两种日晷的“晷针”重合,n小时后,两种日晷对应的时刻一致,即两种晷“晷针”的影子所在的直线相交于点.此时,与满足的关系式__________.
【变式1-3】.如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是_________投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
考点2 中心投影
【例2-1】.下列哪种光线形成的投影不是中心投影( )
A.台灯 B.太阳 C.手电筒 D.路灯
【例2-2】.如图,白炽灯正下方有一个乒乓球,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子( )
A.越来越大 B.越来越小 C.先变大后变小 D.先变小后变大
【变式2--1】.下列选项能正确反映小亮和小美在同一盏路灯的两侧站立时影子情况的是( )
A. B.
C. D.
【变式2-2】.广场上有一个高20米的路灯,一天晚上,身高1.65米的小刚路过这里,发现自己的影长是身高的2倍,这时小刚离路灯的距离是_________米.
【变式2-3】.在一直线上有几根竹竿.它们在同一灯光下的影子如图所示(图中的粗线段).
(1)根据灯光下的影子确定光源的位置;
(2)画出竹竿AB的影子(用线段表示);
(3)画出影子为CD的竹竿(用线段表示).
考点3 视点、视角、盲区
【例3-1】.如图,区域为驾驶员的盲区,驾驶员视线与地面的夹角,视线与地面的夹角,点为视线与车窗底端的交点,.若A点到B点的距离,则盲区中的长度是( )
(参考数据:)
A.2.6m B.2.8m C.3.4m D.4.5m
【变式3-1】.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A. B.
C. D.四边形
【变式3-2】.最佳视点
如图1,设墙壁上的展品最高处点P距底面a米,最低处的点Q距底面b米,站在何处观赏最理想?所谓观赏理想是指看展品的视角最大,问题转化为在水平视线EF上求使视角最大的点.
如图2,当过P、Q、E三点的圆与过点E的水平线相切于点E时,视角最大,站在此处观赏最理想,小明同学想这是为什么呢?他在过点E的水平线上任取异于点E的点,连接交于点F,连接,…
任务一:请按照小明的思路,说明在点E时视角最大;
任务二:若,,观察者的眼睛距地面的距离为1.5米,最大视角为,求观察者应该站在距离多远的地方最理想(结果精确到0.01米,参考数据).
考点4 判断几何体的三视图
【例4-1】.篆刻是中华传统艺术之一,雕刻印章是篆刻基本功.如图是一块雕刻印章的材料,其俯视图为( )
A. B. C. D.
【例4-2】.下列几何体都是由相同的小立方体搭成的,几何体的左视图与其他三个不同的是( )
A. B. C. D.
【变式4-1】.如图,是由几个大小完全一样的小正方体搭成的几何体,该几何体从左面看的形状图是( )
A. B.
C. D.
【变式4-2】..如图是平面切割正方体得到的几何体,该几何体的主视图是( )
A. B. C. D.
【变式4-3】..榫卯是古代中国建筑、家具等的主要结构方式,如图是某个部件“卯”的实物图,它的左视图是( )
A. B. C. D.
考点5 画几何体的三视图
【例5-1】.请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
【例5-2】.一个零件是由长为、高和宽都为的长方体与直径为、高度为的半圆柱组成几何体后,又切去直径为的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.
【变式5-1】.从大正方体中挖去一个小正方体,得到一个如图所示的零件,画出该零件的三视图.
【变式5-2】.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
A. B.
C. D.
【变式5-3】.用五个相同的正方体搭成如图所示的立体图形,则该立体图形的主视图是( )
A. B. C. D.
考点6由三视图确定几何体
【例6-1】.如图是一个立体图形的三视图,该立体图形是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
【例6-2】.如图为某几何体的三种视图,这个几何体可以是( )
A. B. C. D.
【变式6-1】.根据三视图,描述这个物体的形状.
变式6-2】.根据三视图,描述这个物体的形状.
【变式6-3】.由5个相同的小正方体搭成的物体的俯视图如图所示,这个物体有几种搭法?
【变式6-4】.根据下列三视图想象物体原形,并分别画出物体的实物图.
考点7 由三视图求几何体的表面积
【例7-1】.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称:______;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
【例7-2】.根据下列三视图,求它们表示的几何体的体积(图中标有尺寸).
【变式7-1】.图(1)是由两个长方体组成的立体图形,图(2)中的长方体是图(1)中的两个长方体的另一种摆放形式,图①②③是从不同的方向看图(1)所得的平面图形.
(1)填空:图①是从___________面看得到的平面图形,图②是从___________面看得到的平面图形,图③是从___________面看得到的平面图形,
(2)请根据各图中所给的信息(单位:cm),计算出图(1)中上面的小长方体的体积.
【变式7-2】.已知某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C. D.
【变式7-3】..如图,是一个底面为等边三角形的正三棱柱和它的主视图及俯视图,则它的左视图的面积是( )
A. B.8 C. D.16
【变式7-4】..如图,计算所给三视图表示的几何体的体积是_____.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
小结与复习
知识体系构建
二、知识点梳理
知识点1 、投影
1.投影:一般地,用光线照射物体,在某个平面(地面或墙壁等)上得到的影子,叫做物体的投影.
2.平行投影:由平行光线形成的投影
(1)等高的物体垂直地面放置时,如图1所示,在太阳光下,它们的影子一样长.
(2)等长的物体平行于地面放置时,如图2所示,它们在太阳光下的影子一样长,且影长等于物体本身的长度.
(3)物高与影长的关系
①在不同时刻,同一物体的影子的方向和大小可能不同.不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚,物体影子的指向是:西→西北→北→东北→东,影长也是由长变短再变长.
②在同一时刻,不同物体的物高与影长成正比例.
即:.
利用上面的关系式可以计算高大物体的高度,比如旗杆的高度等.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
3.中心投影:若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影.这个“点”就是中心,相当于物理上学习的“点光源”
(1)等高的物体垂直地面放置时,如图1所示,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
(2)等长的物体平行于地面放置时,如图2所示.一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
在中心投影的情况下,还有这样一个重要结论:点光源、物体边缘上的点以及它在影子上的对应点在同一条直线上,根据其中两个点,就可以求出第三个点的位置.
知识点2 、平行投影与中心投影的区别与联系
1.联系:
(1)中心投影、平行投影都是研究物体投影的一种,只不过平行投影是在平行光线下所形成的投影,通常的平行光线有太阳光线、月光等,而中心投影是从一点发出的光线所形成的投影,通常状况下,灯泡的光线、手电筒的光线等都可看成是从某一点发射出来的光线.
(2)在平行投影中,同一时刻改变物体的方向和位置,其投影也跟着发生变化;在中心投影中,同一灯光下,改变物体的位置和方向,其投影也跟着发生变化.在中心投影中,固定物体的位置和方向,改变灯光的位置,物体投影的方向和位置也要发生变化.
2.区别:
(1)太阳光线是平行的,故太阳光下的影子长度都与物体高度成比例;灯光是发散的,灯光下的影子与物体高度不一定成比例.
(2)同一时刻,太阳光下影子的方向总是在同一方向,而灯光下的影子可能在同一方向,也可能在不同方向.
知识点3 、三视图
1 .正投影
正投影的定义:
如图所示,图(1)中的投影线集中于一点,形成中心投影;图(2)(3)中,投影线互相平行,形成平行投影;图(2)中,投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
(1)线段的正投影分为三种情况.如图所示.
①线段AB平行于投影面P时,它的正投影是线段A1B1,与线段AB的长相等;
②线段AB倾斜于投影面P时,它的正投影是线段A2B2,长小于线段AB的长;
③线段AB垂直于投影面P时,它的正投影是一个点.
(2)平面图形正投影也分三种情况,如图所示.
①当平面图形平行于投影面Q时,它的正投影与这个平面图形的形状、大小完全相同,即正投影与这个平面图形全等;
②当平面图形倾斜于投影面Q时,平面图形的正投影与这个平面图形的形状、大小发生变化,即会缩小,是类似图形但不一定相似.
③当平面图形垂直于投影面Q时,它的正投影是直线或直线的一部分.
(3)立体图形的正投影.
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最大截面全等.
2 .三视图
(1).三视图的概念
①视图
从某一角度观察一个物体时,所看到的图象叫做物体的一个视图.
②正面、水平面和侧面
用三个互相垂直的平面作为投影面,其中正对我们的面叫做正面,正面下面的面叫做水平面,右边的面叫做侧面.
③三视图
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.主视图、左视图、俯视图叫做物体的三视图.
(2).三视图之间的关系
①位置关系
三视图的位置是有规定的,主视图要在左边,它的下方应是俯视图,左视图在其右边,如图(1)所示.
②大小关系
三视图之间的大小是相互联系的,遵循主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等的原则.如图(2)所示.
知识点4 、画几何体的三视图
画图方法:
画一个几何体的三视图时,要从三个方面观察几何体,具体画法如下:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
几何体上被其他部分遮挡而看不见的部分的轮廓线应画成虚线.
知识点5、由三视图想象几何体的形状
由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象主体图的前面、上面和左侧面,然后综合起来考虑整体图形.
三、高频考点
考点1 平行投影
【例1-1】.在平行投影下,矩形的投影不可能是( )
A. B. C. D.
答案:A
解析:因为矩形的投影是在平行投影下,所以对边平行或重合成一条线段,故选项A错误.故选A.
【例1-2】.下列说法正确的是( )
A.物体在阳光下的投影只与物体的高度有关
B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.
C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.
D.物体在阳光照射下,影子的长度和方向都是固定不变的.
答案:C
解析:A、物体在阳光下的投影不只与物体的高度有关,还与时刻有关,错误;
B、小明的个子比小亮高,在不同的时间,小明的影子可能比小亮的影子短,错误;
C、不同时刻物体在太阳光下的影子的大小在变,方向也在改变,正确;
D、不同时刻物体在太阳光下的影子的大小在变,方向也在改变,错误.
故选:C.
【变式1-1】.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③—④—①—② B.②—①—④—③
C.④—①—②—③ D.④—①—③—②
答案:B
解析:众所周知,影子方向的变化是上午时朝向西边,中午时朝向北边,下午时朝向东边;
影子长短的变化是由长变短再变长,结合方向和长短的变化即可得出答案
故选:B.
【变式1-2】.日晷是我国古代利用日影测定时刻的一种计时仪器,它由“晷面”和“晷针”组成,古人常用的日晷有水平式日晷(图1)和赤道式日晷(图2).其中水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度且“晷面”与地面平行;赤道式日晷的“晷面”与赤道面平行当太阳光照在日晷上时,晷针的影子就会投向晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以此来显示时刻.此外,水平式日晷的“晷面”刻度不均匀,赤道式日晷的“晷面”刻度则是均匀的.
(1)如图1,当水平式日晷放在纬度为(即)位置时,晷针与晷面的夹角为__________°.
(2)如图3,将两种日晷的“晷针”重合,n小时后,两种日晷对应的时刻一致,即两种晷“晷针”的影子所在的直线相交于点.此时,与满足的关系式__________.
答案:(1)
(2)
解析:(1)水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度,
当水平式日晷放在纬度为(即)位置时,晷针与晷面的夹角为;
故答案为:;
(2)过点作于点E,如图所示:
则,
,
根据题意可知,赤道日晷的晷面与晷针垂直,
,
,
,
,
根据平行投影可知,当12点时,点在水平方向的投影为点E,经过n小时后,的投影在上,因此,
,
.
故答案为:.
【变式1-3】.如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是_________投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
答案:(1)平行
(2)7米
解析:(1)平行
(2)如图,过点E作于点M,过点G作于点N.
则米,米,米,米,(米).由平行投影的性质可知,即,米,即电线杆的高度为7米.
考点2 中心投影
【例2-1】.下列哪种光线形成的投影不是中心投影( )
A.台灯 B.太阳 C.手电筒 D.路灯
答案:B
解析:中心投影的光源为蜡烛、台灯、路灯这样的光,而平行投影的光源为太阳光与月光,由此可得形成的投影不是中心投影的是太阳,
故答案选择:B.
【例2-2】.如图,白炽灯正下方有一个乒乓球,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子( )
A.越来越大 B.越来越小 C.先变大后变小 D.先变小后变大
答案:B
解析:根据中心投影的特点,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子越来越小,
故选:B.
【变式2--1】.下列选项能正确反映小亮和小美在同一盏路灯的两侧站立时影子情况的是( )
A. B.
C. D.
答案:D
解析:小亮和小美在同一盏路灯的两侧站立时影子情况应如图所示:
故选D.
【变式2-2】.广场上有一个高20米的路灯,一天晚上,身高1.65米的小刚路过这里,发现自己的影长是身高的2倍,这时小刚离路灯的距离是_________米.
答案:36.7
解析:如图,由题意可得米,米,米,
,.设米,则米,,解得,小刚离路灯的距离是36.7米.
【变式2-3】.在一直线上有几根竹竿.它们在同一灯光下的影子如图所示(图中的粗线段).
(1)根据灯光下的影子确定光源的位置;
(2)画出竹竿AB的影子(用线段表示);
(3)画出影子为CD的竹竿(用线段表示).
答案:(1)见解析
(2)见解析
(3)见解析
解析:(1)如图,点P即为光源所在的位置.
(2)BE即为竹竿AB的影子.
(3)CF是影子为CD的竹竿.
考点3 视点、视角、盲区
【例3-1】.如图,区域为驾驶员的盲区,驾驶员视线与地面的夹角,视线与地面的夹角,点为视线与车窗底端的交点,.若A点到B点的距离,则盲区中的长度是( )
(参考数据:)
A.2.6m B.2.8m C.3.4m D.4.5m
答案:B
解析:本题考查解直角三角形的实际应用、矩形的判定和性质.
,
∴四边形为矩形.
由题意得,
.
,故选B.
【变式3-1】.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A. B.
C. D.四边形
答案:C
解析:由图知:在视点E的位置,看不到段,因此监视器的盲区在所在的区域,
故选:C.
【变式3-2】.最佳视点
如图1,设墙壁上的展品最高处点P距底面a米,最低处的点Q距底面b米,站在何处观赏最理想?所谓观赏理想是指看展品的视角最大,问题转化为在水平视线EF上求使视角最大的点.
如图2,当过P、Q、E三点的圆与过点E的水平线相切于点E时,视角最大,站在此处观赏最理想,小明同学想这是为什么呢?他在过点E的水平线上任取异于点E的点,连接交于点F,连接,…
任务一:请按照小明的思路,说明在点E时视角最大;
任务二:若,,观察者的眼睛距地面的距离为1.5米,最大视角为,求观察者应该站在距离多远的地方最理想(结果精确到0.01米,参考数据).
答案:任务一:见解析
任务二:观察者应该站在距离0.87米的地方最理想
解析:任务一:过点E的水平线上任取异于点E的点,连接交于点F,连接,
是的外角,
,
又与都是弧所对的圆周角,
,
,
在点E时视角最大.
任务二:,
,
又,
是等边三角形,.
如图2,连接,
是的切线,
,
,
,
,
又,
四边形是平行四边形,
,
.
由题意得,(米),
在中,(米).
答:观察者应该站在距离0.87米的地方最理想.
考点4 判断几何体的三视图
【例4-1】.篆刻是中华传统艺术之一,雕刻印章是篆刻基本功.如图是一块雕刻印章的材料,其俯视图为( )
A. B. C. D.
答案:D
解析:
【例4-2】.下列几何体都是由相同的小立方体搭成的,几何体的左视图与其他三个不同的是( )
A. B. C. D.
答案:D
解析:
【变式4-1】.如图,是由几个大小完全一样的小正方体搭成的几何体,该几何体从左面看的形状图是( )
A. B.
C. D.
答案:B
解析:从左边看,底层是两个小正方形,上层的左边是一个小正方形,
故选:B.
【变式4-2】..如图是平面切割正方体得到的几何体,该几何体的主视图是( )
A. B. C. D.
答案:B
解析:
【变式4-3】..榫卯是古代中国建筑、家具等的主要结构方式,如图是某个部件“卯”的实物图,它的左视图是( )
A. B. C. D.
答案:D
解析:从左边看到的平面图形是,
故选:D.
考点5 画几何体的三视图
【例5-1】.请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
答案:作图见解析
解析:从正面可以看到5个正方形,分3列,依次为3个,1个,1个,
所以从正面看的主视图为:
从左面可以看到4个正方形,分2列,依次为3个,1个,
所以从左面看的左视图为:
从上面可以看到4个正方形,分3列,依次为1个,2个,1个,
所以从上面看的俯视图为:
【例5-2】.一个零件是由长为、高和宽都为的长方体与直径为、高度为的半圆柱组成几何体后,又切去直径为的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.
答案:见解析
解析:三视图如图所示:
【变式5-1】.从大正方体中挖去一个小正方体,得到一个如图所示的零件,画出该零件的三视图.
答案:见解析
解析:如图:
【变式5-2】.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
A. B.
C. D.
答案:D
解析:从左边看,是一个矩形,矩形的中间有一条横向的虚线.
故选:D.
【变式5-3】.用五个相同的正方体搭成如图所示的立体图形,则该立体图形的主视图是( )
A. B. C. D.
答案:B
解析:解:根据主视图的意义可知,从正面看到四个正方形,
故选:B.
考点6由三视图确定几何体
【例6-1】.如图是一个立体图形的三视图,该立体图形是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
答案:D
解析:由主视图和左视图为三角形判断出是锥体,
根据俯视图是圆可判断出这个几何体应该是圆锥.
故选:D.
【例6-2】.如图为某几何体的三种视图,这个几何体可以是( )
A. B. C. D.
答案:A
解析:根据几何体的三视图,只有A选项符合题意;
故选:A.
【变式6-1】.根据三视图,描述这个物体的形状.
答案:这个物体是正六棱柱
解析:
变式6-2】.根据三视图,描述这个物体的形状.
答案:见解析
解析:该物体由六个小正方体构成,只有一排,最底层是三个小正方体,中间一层是两个小正方体,且这两个小正方体靠右放置,上面一层是一个小正方体,且靠右放置(如图所示).
【变式6-3】.由5个相同的小正方体搭成的物体的俯视图如图所示,这个物体有几种搭法?
答案:3种
解析:这个物体的搭法有3种,如图所示.
【变式6-4】.根据下列三视图想象物体原形,并分别画出物体的实物图.
答案:见解析
解析:图(1)、图(2)的物体的实物图如下所示:
考点7 由三视图求几何体的表面积
【例7-1】.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称:______;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
答案:(1)长方体或四棱柱
(2)
解析:(1)∵这个立方体的三视图都是长方形,
∴这个立方体是长方体或四棱柱.
(2)由三视图知该长方体的表面积:.
【例7-2】.根据下列三视图,求它们表示的几何体的体积(图中标有尺寸).
答案:(1)
(2)
解析:(1)由三视图知该几何体由两个圆柱组成,其中小圆柱在大圆柱的正上方.
,,
故.
(2)由三视图知该几何体的体积为一个长方体和一个半圆柱的体积和.
,
,
故.
【变式7-1】.图(1)是由两个长方体组成的立体图形,图(2)中的长方体是图(1)中的两个长方体的另一种摆放形式,图①②③是从不同的方向看图(1)所得的平面图形.
(1)填空:图①是从___________面看得到的平面图形,图②是从___________面看得到的平面图形,图③是从___________面看得到的平面图形,
(2)请根据各图中所给的信息(单位:cm),计算出图(1)中上面的小长方体的体积.
答案:(1)正或后;上;左或右
(2)
解析:(1)正或后;上;左或右
(2)由题图可得解得所以题图(1)中上面的小长方体的长、宽、高分别为,,,所以,即题图(1)中上面的小长方体的体积为.
【变式7-2】.已知某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C. D.
答案:D
解析:由三视图知该几何体是三棱柱与半圆柱的组合体,且三棱柱的底面是边长为2的正三角形,三棱柱的高为2;半圆柱的底面半径为1,高为2,该几何体的体积为
.故选D.
【变式7-3】..如图,是一个底面为等边三角形的正三棱柱和它的主视图及俯视图,则它的左视图的面积是( )
A. B.8 C. D.16
答案:C
解析:由三视图可知:底面等边三角形的边长为4,该几何体的高为4,
该几何体的左视图为长方形,
该长方形的长为该几何体的高4,宽为底面等边三角形的高,
底面等边三角形的高=,
它的左视图的面积是,
故选:C.
【变式7-4】..如图,计算所给三视图表示的几何体的体积是_____.
答案:
解析:由三视图可知几何体是下部为底面半径为4,高为8的圆柱,上部是底面半径为2,高为2的圆柱,
所以所求几何体的体积为:;
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
