专题7 反比例函数 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 专题7 反比例函数 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习 |  | |
| 格式 | docx | ||
| 文件大小 | 248.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:34:27 | ||
图片预览




文档简介
专题7 反比例函数
1.反比例函数的三种形式是 、 、 (k≠0,k 是常数),其自变量的取值范围是 .反比例函数的图象是 ,当k 时,双曲线的两个分支在第一、三象限,在 ,y随x的增大而 ;当k 时,双曲线的两个分支在第二、四象限,在 ,y随x的增大而 .反比例函数的图象是关于 对称的中心对称图形,又是 图形,其对称轴为 .双曲线与 x 轴、y轴都没有 ,两个分支 坐标轴,但永远 坐标轴.
2.反比例函数的反比例系数|k|的几何意义:过反比例函数 的图象上任一点 P 作 、 的垂线 PM,PN,则所得的矩形 PMON 的面积为S= 即S= .
实战演练
1.反比例函数 的图象分别位于 ( )
A.第一、第三象限
B.第一、第四象限
C.第二、第三象限
D.第二、第四象限
2.点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数 图象上,则 y1,y2,y3,y4中最小的是 ( )
A. y1 B. y2
C. y3 D. y4
3.已知点 A(x1,y1),B(x2,y2)在反比例函数 的图象上,且 x2,则下列结论一定正确的是 ( )
4.一次函数y= mx+n的图象与反比例函数 的图象交于点 A、B,其中点 A、B的坐标为 B(m,1),则△OAB的面积是 ( )
A.3 B.
C. D.
5.一次函数 与反比例函数 的图象交于点 A(-1,-2),点 B(2,1).当.y1A. x<-1
B.-12
C.0D.06.若点 A(a-1,y1),B(a+1,y2)在反比例函数 的图象上,且y1>y2,则a的取值范围是( )
A. a<-1
B.-1C. a>1
D. a<-1或a>1
7.根据物理学知识,在压力不变的情况下,某物体承受的压强 p(Pa)是它的受力面积 S(m )的反比例函数,其函数图象如图所示.当S=0.25 m 时,该物体承受的压强p的值为 Pa.
8.已知反比例函数 的 图 象 经 过 点 (4, a),则 a 的 值为 .
9.若A(1,y1),B(3,y2)是反比例函数 图象上的两点,则y1、y2 的大小关系是 y1 y2.(填“>”、“=”或“<”)
10.已知点A(a,y1),B(a+1,y2)在反比例函数 (m是常数)的图象上,且. ,则a 的取值范围是 .
11.密闭容器内有一定质量的气体,当容器的体积 V(单位:m )变化时,气体的密度ρ(单位:kg/m )随之变化.已知密度ρ与体积V 是反比例函数关系,它的图象如图所示.
(1)求密度ρ关于体积V 的函数解析式.
(2)当 时,求该气体的密度ρ.
12.设函数 函数 b是常数,
(1)若函数 和函数 的图象交于点 A(1,m),点 B(3,1),
①求函数 , 的表达式;
②当2(2)若点 C(2,n)在函数 的图象上,点 C先向下平移2 个单位,再向左平移4个单位,得点 D,点D 恰好落在函数的图象上,求n的值.
13在直角坐标系中,设函数 是常数,>0,x>0)与函数 是常数, 的图象交于点 A,点A 关于 y轴的对称点为点 B.
(1)若点 B 的坐标为(-1,2),
①求 , 的值;
②当<时,直接写出x的取值范围;
(2)若点 B 在函数 是常数,k ≠0)的图象上,求 的值.
14.如图,反比例函数 y= 的图象与y=2x的图象相交于点C,过直线上点 A(a,8)作 AB⊥y轴交于点 B,交反比例函数图象于点 D,且AB=4BD.
(1)求反比例函数的解析式;
(2)求四边形OCDB 的面积.
压轴预测
1.已知点 A(2,-3)关于x轴的对称点A'在反比例函数 的图象上,则实数 k 的值为 ( )
A. -6 B.
C.6
2.如图,是三个反比例函数 在y 轴右侧的图象,则 ( )
3.已知点A(,),B(+1,)都在反比例函数 的图象上, ( )
A.若 则
B.若 则
C.若( 则
D.若 则
4.如图,在平面直角坐标系中,矩形 ABCD四个顶点 的坐标分别为 A (-1,2),B(-1,-1),C(3,-1),D(3,2),当双曲线 与矩形有四个交点时,k的取值范围是 ( )
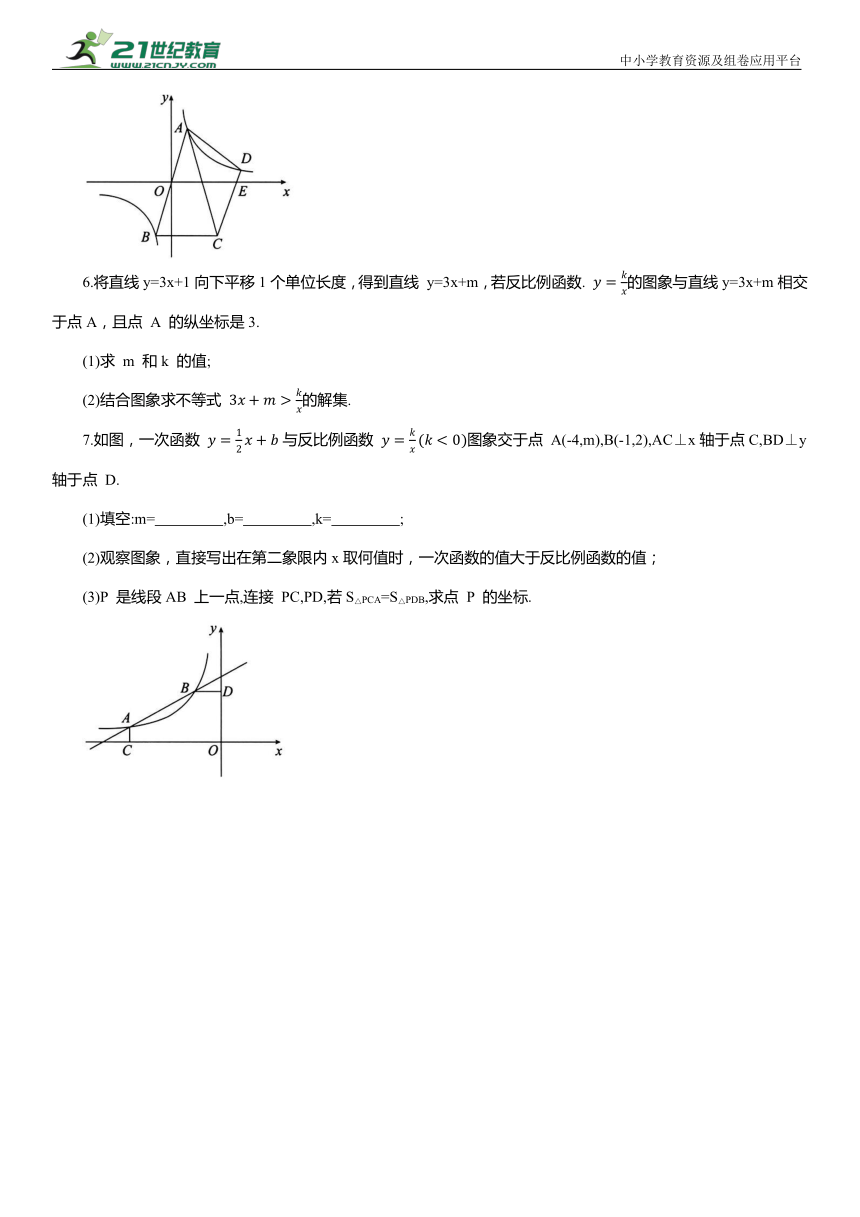
A.0C. k>1 D.05.如图,在平面直角坐标系中,点A,B分别落在双曲线 第一和第三象限的两支上,连接AB,线段 AB 恰好经过原点O,以 AB 为腰作等腰三角形 ABC,AB=AC,点 C 落在第四象限中,且 BC∥x轴.过点 C作CD∥AB交x轴于 E 点,交双曲线第一象限一支于 D 点,若△ACD的面积为 则k= .
6.将直线y=3x+1向下平移1个单位长度,得到直线 y=3x+m,若反比例函数. 的图象与直线y=3x+m相交于点A,且点 A 的纵坐标是3.
(1)求 m 和k 的值;
(2)结合图象求不等式 的解集.
7.如图,一次函数 与反比例函数 图象交于点 A(-4,m),B(-1,2),AC⊥x轴于点C,BD⊥y轴于点 D.
(1)填空:m= ,b= ,k= ;
(2)观察图象,直接写出在第二象限内x取何值时,一次函数的值大于反比例函数的值;
(3)P 是线段AB 上一点,连接 PC,PD,若S△PCA=S△PDB,求点 P 的坐标.
参考答案
双曲线 >0 每一象限内 减小 <0每一象限内 增大 原点 轴对称直线 y=±x 交点 无限接近于交不到
2. x轴 y轴|y|·|x|=| xy| |k|
1. A 【解析】本题考查反比例函数的图象与性质.因为反比例函数 中k=6>0,所以其图象位于第一、第三象限,故选 A.
2. D 【解析】本题考查反比例函数的图象与性质.由题意知 最.小的是 y ,故选 D.
3. C 【解析】本题考查反比例函数的图象和性质.∵双曲线 分别位于第一、三象限,且 y ,故选C.
4. D 【解析】本题考查一次函数与反比例函数的交点问题、三角形的面积公式.由题知 解得 所以A(- ,-4),B(2,1),一次函数的解析式为y=2x-3,令y=0,得. 所以一次函数与x轴的交点为( ,所以△OAB的面积是 故选 D.
5. D 【解析】本题考查一次函数与反比例函数的图象与性质.利用图象法求解,根据两点坐标求出函数解析式并画出函数图象,从而确定当y6. B 【解析】本题考查反比例函数的图象与性质.∵k<0,∴在图象的每一支上,y随x的增大而增大,当点 A(a-1,y ),B(a+1,y )在图象的同一支上时,∵y >y ,∴a-1>a+1,此不等式无解;当点A(a-1,y ),B(a+1,y )分别在图象的两支上时,∵ 1>0,解得 - 1解答本题的关键是掌握当 k<0时,在 图象的每一支上,y随x的增大而增大.
7.400 【解析】本题考查反比例函数的实际应用.由题知, 即 当 S=0.25 m 时, 400(Pa).
【解析】本题考查反比例函数图象上点的坐标特征.将点(4,a)代入 得
9.< 【解析】本题考查反比例函数的图象与性质.∵m< 则反比例函数的图象经过第二、四象限,∴点A,B在第四象限.∵第四象限内,函数y随x的增大而增大,
10.-10,解得-1(1)根据图象上点 A 的坐标,利用待定系数法即可求解;(2)将V=10代入(1)中的函数解析式,即可求解.
解:(1)设密度ρ关于体积V 的函数解析式为 (V>0,k≠0).
把V=4,ρ=2.5代入 得
解得k=10.
所以密度ρ关于体积V的函数解析式为
(2)当V=10时.
所以该气体的密度为1 kg/m .
评分说明:(1)k写成m 等其他字母均可.
(2)不写V>0,k≠0均不扣分.
(2)1
13.(1)①k1=2,k2=2 ②x>1 (2)0
14.(1)y= (2)10
(1)根据点 A 纵坐标求得a 的值,然后根据 AB⊥y轴与AB=4BD求得点D 的坐标,从而求得反比例函数的解析式;(2)先求得两函数交点 C 的坐标,再利用△ABO与△ADC面积之差计算四边形OCDB 的面积.
解:(1)由点A(a,8)在y=2x上,则a=4,
∴A(4,8).
∵AB⊥ y 轴, 与 反 比 例 函 数 图 象 交 于 点 D,且 AB=4BD,
∴BD=1,即 D(1,8).
∴k=8,反比例函数解析式为
(2)∵C是直线y=2x与反比例函数 图象的交点,
∵x>0,
∴x=2,则C(2,4).
压轴预测
1. C 【解析】本题考查反比例函数图象和对称性.由题意得点 A(2,-3)关于x轴的对称点A'的坐标为(2,3),把点A'(2,3)代入 得k=2×3=6,故选C.
2. C 【解析】本题考查反比例函数的图象与性质.由反比例函数的性质可知,若k>0,那么k的值越大,图象离坐标轴越远,. .又y 的图象在第四象限,∴k < ,故选 C.
3. C
4. D 【解析】本题考查反比例函数的图象与性质.由题可知,当双曲线 经过点 B(-1,-1)时,双曲线与矩形ABCD有三个交点,此时k=-1×(-1)=1.根据反比例函数的对称性,结合图象可知,当05.2 【解析】本题考查一次函数和反比例函数的图象与性质、三角形的面积公式.如图,过点 A 作 AF⊥BC 于点F,连接BD,设点 A 的坐标为(a,k),a>0,则点 B的坐标为(-a,-k/a).∵AB=AC,∴BF=CF=a-(-a)=2a,∴ BC = 2BF = 4a,∴ 点 C 的 坐标为 设直线AB的解析式为y= mx,代入点A的坐标,得 即直线 AB 的解析式为y= kzx.∵CD∥AB,∴设直线CD的解析式为 将点 C坐标代入得 直线CD的解析式为 由 可得 ( 舍负 ), ∴点 D 的 坐 标 为 ∵AB∥CD,∴S△BCD = S△ACD = 又 解得k=2.
6.(1)m=0,k=3 (2)x>1或-1(1)根据直线平移后的方程得到 m 的值,进而得到点A 的坐标,根据点 A 在反比例函数的图象上得到k的值;(2)画出两函数的图象,数形结合求解不等式或将不等式转换为不等式组求解.
解:(1)∵将直线y=3x+1向下平移1个单位长度,得到直线 y=3x+m,
∴3x+1-1=3x+m,
∴m=0.
∵反比例函数 的图象与直线y=3x+m相交于点A,且点 A 的纵坐标是3,
∴将 y=3代入 y=3x得3x=3,x=1,
∴A(1,3).
∵点 A(1,3)在反比例函数 图象上,
综上所述,m=0,k=3.
(2)求不等式 的解集有以下两种解法:
解法一:如图,在平面直角坐标系中画出y=3x与 的图象.
∵y=3x与 的图象都是中心对称图形,
点 A(1,3)关于原点的对称点为(-1,-3).
由图象可知:当x>1或-1∴不等式 的解集为x>1或-1解法二:
中小学教育资源及组卷应用平台
或
或 或x<-1
∴x>1或-1∴不等式 的解集为x>1或-1(1) , ,-2
(2)-4(1)将点 B的坐标代入反比例函数和一次函数的表达式即可求出k 和b的值,再将点 A 的坐标代入一次函数的表达式中,即可求出 m的值;(2)根据两个函数图象的位置关系结合A,B两点的坐标,即可写出x的取值范围;(3)设出 P 点的坐标,分别表示出△PCA 和△PDB 的面积,列方程即可求解.
解:
(2)当-4(3)由(1)可知,一次函数
设 P点坐标为
∵△PCA 和△PDB的面积相等,
解得
∴P点坐标为
1.反比例函数的三种形式是 、 、 (k≠0,k 是常数),其自变量的取值范围是 .反比例函数的图象是 ,当k 时,双曲线的两个分支在第一、三象限,在 ,y随x的增大而 ;当k 时,双曲线的两个分支在第二、四象限,在 ,y随x的增大而 .反比例函数的图象是关于 对称的中心对称图形,又是 图形,其对称轴为 .双曲线与 x 轴、y轴都没有 ,两个分支 坐标轴,但永远 坐标轴.
2.反比例函数的反比例系数|k|的几何意义:过反比例函数 的图象上任一点 P 作 、 的垂线 PM,PN,则所得的矩形 PMON 的面积为S= 即S= .
实战演练
1.反比例函数 的图象分别位于 ( )
A.第一、第三象限
B.第一、第四象限
C.第二、第三象限
D.第二、第四象限
2.点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数 图象上,则 y1,y2,y3,y4中最小的是 ( )
A. y1 B. y2
C. y3 D. y4
3.已知点 A(x1,y1),B(x2,y2)在反比例函数 的图象上,且 x2,则下列结论一定正确的是 ( )
4.一次函数y= mx+n的图象与反比例函数 的图象交于点 A、B,其中点 A、B的坐标为 B(m,1),则△OAB的面积是 ( )
A.3 B.
C. D.
5.一次函数 与反比例函数 的图象交于点 A(-1,-2),点 B(2,1).当.y1
B.-1
C.0
A. a<-1
B.-1
D. a<-1或a>1
7.根据物理学知识,在压力不变的情况下,某物体承受的压强 p(Pa)是它的受力面积 S(m )的反比例函数,其函数图象如图所示.当S=0.25 m 时,该物体承受的压强p的值为 Pa.
8.已知反比例函数 的 图 象 经 过 点 (4, a),则 a 的 值为 .
9.若A(1,y1),B(3,y2)是反比例函数 图象上的两点,则y1、y2 的大小关系是 y1 y2.(填“>”、“=”或“<”)
10.已知点A(a,y1),B(a+1,y2)在反比例函数 (m是常数)的图象上,且. ,则a 的取值范围是 .
11.密闭容器内有一定质量的气体,当容器的体积 V(单位:m )变化时,气体的密度ρ(单位:kg/m )随之变化.已知密度ρ与体积V 是反比例函数关系,它的图象如图所示.
(1)求密度ρ关于体积V 的函数解析式.
(2)当 时,求该气体的密度ρ.
12.设函数 函数 b是常数,
(1)若函数 和函数 的图象交于点 A(1,m),点 B(3,1),
①求函数 , 的表达式;
②当2
13在直角坐标系中,设函数 是常数,>0,x>0)与函数 是常数, 的图象交于点 A,点A 关于 y轴的对称点为点 B.
(1)若点 B 的坐标为(-1,2),
①求 , 的值;
②当<时,直接写出x的取值范围;
(2)若点 B 在函数 是常数,k ≠0)的图象上,求 的值.
14.如图,反比例函数 y= 的图象与y=2x的图象相交于点C,过直线上点 A(a,8)作 AB⊥y轴交于点 B,交反比例函数图象于点 D,且AB=4BD.
(1)求反比例函数的解析式;
(2)求四边形OCDB 的面积.
压轴预测
1.已知点 A(2,-3)关于x轴的对称点A'在反比例函数 的图象上,则实数 k 的值为 ( )
A. -6 B.
C.6
2.如图,是三个反比例函数 在y 轴右侧的图象,则 ( )
3.已知点A(,),B(+1,)都在反比例函数 的图象上, ( )
A.若 则
B.若 则
C.若( 则
D.若 则
4.如图,在平面直角坐标系中,矩形 ABCD四个顶点 的坐标分别为 A (-1,2),B(-1,-1),C(3,-1),D(3,2),当双曲线 与矩形有四个交点时,k的取值范围是 ( )
A.0
6.将直线y=3x+1向下平移1个单位长度,得到直线 y=3x+m,若反比例函数. 的图象与直线y=3x+m相交于点A,且点 A 的纵坐标是3.
(1)求 m 和k 的值;
(2)结合图象求不等式 的解集.
7.如图,一次函数 与反比例函数 图象交于点 A(-4,m),B(-1,2),AC⊥x轴于点C,BD⊥y轴于点 D.
(1)填空:m= ,b= ,k= ;
(2)观察图象,直接写出在第二象限内x取何值时,一次函数的值大于反比例函数的值;
(3)P 是线段AB 上一点,连接 PC,PD,若S△PCA=S△PDB,求点 P 的坐标.
参考答案
双曲线 >0 每一象限内 减小 <0每一象限内 增大 原点 轴对称直线 y=±x 交点 无限接近于交不到
2. x轴 y轴|y|·|x|=| xy| |k|
1. A 【解析】本题考查反比例函数的图象与性质.因为反比例函数 中k=6>0,所以其图象位于第一、第三象限,故选 A.
2. D 【解析】本题考查反比例函数的图象与性质.由题意知 最.小的是 y ,故选 D.
3. C 【解析】本题考查反比例函数的图象和性质.∵双曲线 分别位于第一、三象限,且 y ,故选C.
4. D 【解析】本题考查一次函数与反比例函数的交点问题、三角形的面积公式.由题知 解得 所以A(- ,-4),B(2,1),一次函数的解析式为y=2x-3,令y=0,得. 所以一次函数与x轴的交点为( ,所以△OAB的面积是 故选 D.
5. D 【解析】本题考查一次函数与反比例函数的图象与性质.利用图象法求解,根据两点坐标求出函数解析式并画出函数图象,从而确定当y
7.400 【解析】本题考查反比例函数的实际应用.由题知, 即 当 S=0.25 m 时, 400(Pa).
【解析】本题考查反比例函数图象上点的坐标特征.将点(4,a)代入 得
9.< 【解析】本题考查反比例函数的图象与性质.∵m< 则反比例函数的图象经过第二、四象限,∴点A,B在第四象限.∵第四象限内,函数y随x的增大而增大,
10.-1
解:(1)设密度ρ关于体积V 的函数解析式为 (V>0,k≠0).
把V=4,ρ=2.5代入 得
解得k=10.
所以密度ρ关于体积V的函数解析式为
(2)当V=10时.
所以该气体的密度为1 kg/m .
评分说明:(1)k写成m 等其他字母均可.
(2)不写V>0,k≠0均不扣分.
(2)1
13.(1)①k1=2,k2=2 ②x>1 (2)0
14.(1)y= (2)10
(1)根据点 A 纵坐标求得a 的值,然后根据 AB⊥y轴与AB=4BD求得点D 的坐标,从而求得反比例函数的解析式;(2)先求得两函数交点 C 的坐标,再利用△ABO与△ADC面积之差计算四边形OCDB 的面积.
解:(1)由点A(a,8)在y=2x上,则a=4,
∴A(4,8).
∵AB⊥ y 轴, 与 反 比 例 函 数 图 象 交 于 点 D,且 AB=4BD,
∴BD=1,即 D(1,8).
∴k=8,反比例函数解析式为
(2)∵C是直线y=2x与反比例函数 图象的交点,
∵x>0,
∴x=2,则C(2,4).
压轴预测
1. C 【解析】本题考查反比例函数图象和对称性.由题意得点 A(2,-3)关于x轴的对称点A'的坐标为(2,3),把点A'(2,3)代入 得k=2×3=6,故选C.
2. C 【解析】本题考查反比例函数的图象与性质.由反比例函数的性质可知,若k>0,那么k的值越大,图象离坐标轴越远,. .又y 的图象在第四象限,∴k < ,故选 C.
3. C
4. D 【解析】本题考查反比例函数的图象与性质.由题可知,当双曲线 经过点 B(-1,-1)时,双曲线与矩形ABCD有三个交点,此时k=-1×(-1)=1.根据反比例函数的对称性,结合图象可知,当0
6.(1)m=0,k=3 (2)x>1或-1
解:(1)∵将直线y=3x+1向下平移1个单位长度,得到直线 y=3x+m,
∴3x+1-1=3x+m,
∴m=0.
∵反比例函数 的图象与直线y=3x+m相交于点A,且点 A 的纵坐标是3,
∴将 y=3代入 y=3x得3x=3,x=1,
∴A(1,3).
∵点 A(1,3)在反比例函数 图象上,
综上所述,m=0,k=3.
(2)求不等式 的解集有以下两种解法:
解法一:如图,在平面直角坐标系中画出y=3x与 的图象.
∵y=3x与 的图象都是中心对称图形,
点 A(1,3)关于原点的对称点为(-1,-3).
由图象可知:当x>1或-1
中小学教育资源及组卷应用平台
或
或 或x<-1
∴x>1或-1
(2)-4
解:
(2)当-4
设 P点坐标为
∵△PCA 和△PDB的面积相等,
解得
∴P点坐标为
同课章节目录
