专题 10 三角形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 专题 10 三角形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 361.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题 10 三角形
1.三角形的分类
(1)三角形按角分为 三角形、 三角形、 三角形.
(2)三角形按边分为 三角形、 三角形.
2.三角形的性质
(1)三角形中任意两边之和 第三边,任意两边之差 第三边.
(2)三角形的内角和为 ,外角与内角的关系:三角形的外角等于
3.三角形中的主要线段
(1)连接三角形 中点的线段叫作三角形的中位线.
(2)中位线的性质:三角形的中位线 于第三边,并且 第三边的 .
(3) 三角形的中线、高线、角平分线都是 .
4.等腰三角形的性质与判定
(1)等腰三角形的两底角 .
(2)等腰三角形底边上的 、底边上的 、顶角的 互 相 ,简称“ ”.
(3)有两个角相等的三角形是 .
5.等边三角形的性质与判定
(1)等边三角形每个角都等于 ,同样具有“ ”的性质.
(2)三个角相等的三角形是 ,三边相等的三角形是 ,一个角等于 60°的 三角形是等边三角形.
6.直角三角形的性质与判定
(1)直角三角形两锐角 .
(2)直角三角形中 30°所对的直角边等于斜边的 .
(3)直角三角形中,斜边的中线等于斜边的 .
(4)勾股定理:
(5)勾股定理的逆定理: ·
7.相似三角形的判定方法有:
(1) 于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;
(2)两个角对应相等的两个三角形 ;
(3)两边对应成 且 的两个三角形相似;
(4)三边 的两个三角形相似.
8.相似三角形的性质有:(1)相似三角形的对应边 ,对应角 ;(2)相似三角形的对应边的 线、对应边上的 的比等于 比,周长之比也等于 比,面积比等于 .
9.全等三角形
(1)全等三角形: 、 的三角形叫作全等三角形.
(2) 三角 形 全 等 的 判 定 方 法 有: 、 、 、 、 .在证明两个三角形全等时,选择三角形全等的五种方法中,至少有一组 ,因此在应用时要养成先找边的习惯.如果选择找到了一组对应边,再找第二组条件:若找到一组对应边则再找这两边的 用“SAS”或再找第三组 用“SSS”;若找到一组角则需找 (可能用“ASA”或“AAS”)或夹这个角的另一组 用“SAS”;若是判定两个 全等则优先考虑“HL”.
(3)全等三角形的性质:全等三角形的 、 ,全等三角形的面积 、周长 、对应高、 、 相等.
10.分析、证明几何题的常用方法
(1) :从命题的题设出发,通过一系列的有关定义、公理、定理的运用,逐步向前推进,直到问题解决.(2) :从命题的结论出发,不断寻找使结论成立的条件,直到已知条件.(3) :将分析法与综合法合并使用,比较起来,分析法利于思考,综合法宜于表达,因此在实际思考问题时,可合并使用灵活处理,以利于缩短题设与结论之间的距离,最后达到完全沟通.
实战演练
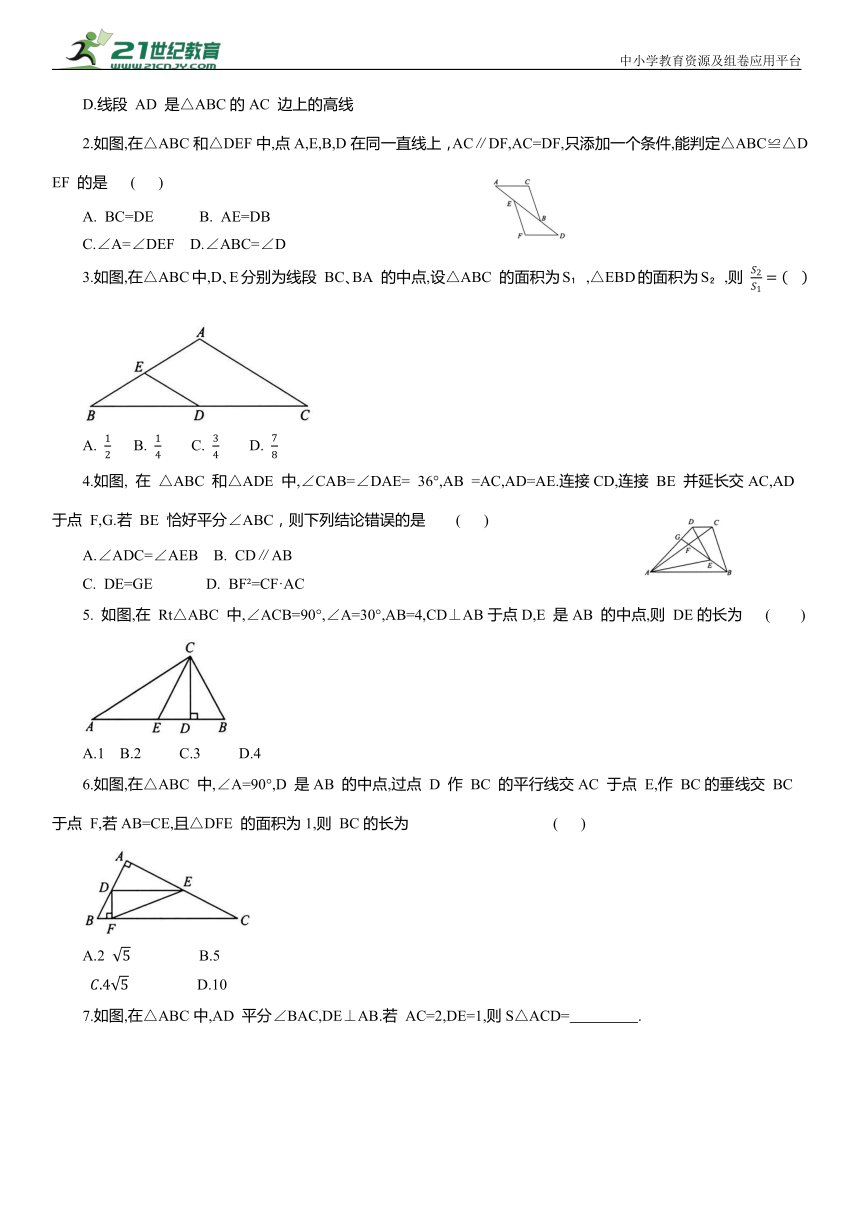
1.如图,CD⊥AB 于点 D,已知∠ABC是钝角,则 ( )
A.线段CD是△ABC的AC 边上的高线
B.线段 CD 是△ABC的AB 边上的高线
C.线段 AD 是△ABC的BC 边上的高线
D.线段 AD 是△ABC的AC 边上的高线
2.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF 的是 ( )
A. BC=DE B. AE=DB
C.∠A=∠DEF D.∠ABC=∠D
3.如图,在△ABC中,D、E分别为线段 BC、BA 的中点,设△ABC 的面积为S ,△EBD的面积为S ,则
A. B. C. D.
4.如图, 在 △ABC 和△ADE 中,∠CAB=∠DAE= 36°,AB =AC,AD=AE.连接CD,连接 BE 并延长交AC,AD 于点 F,G.若 BE 恰好平分∠ABC,则下列结论错误的是 ( )
A.∠ADC=∠AEB B. CD∥AB
C. DE=GE D. BF =CF·AC
5. 如图,在 Rt△ABC 中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E 是AB 的中点,则 DE的长为 ( )
A.1 B.2 C.3 D.4
6.如图,在△ABC 中,∠A=90°,D 是AB 的中点,过点 D 作 BC 的平行线交AC 于点 E,作 BC的垂线交 BC 于点 F,若AB=CE,且△DFE 的面积为1,则 BC的长为 ( )
A.2 B.5
D.10
7.如图,在△ABC中,AD 平分∠BAC,DE⊥AB.若 AC=2,DE=1,则S△ACD= .
8. 如图,在 Rt△ABC中,∠ABC=90°,ED是AC 的垂直平分线,交AC 于点D,交 BC 于点 E,∠BAE=10°,则∠C的度数是 .
9.如图,在 Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= °.
10如图,AC 平 分 ∠DCB,CB=CD,DA 的延长线交BC 于点 E,若∠EAC = 49°, 则 ∠BAE 的 度 数为
11.如图,点 B,F,C,E 在同一条 直 线 上, BF = EC, AB = DE,∠B=∠E.
求证:∠A=∠D.
12.如图,在 Rt△ACB中,∠ACB=90°,点 M 为边AB 的中点,点 E在线段 AM 上,EF⊥AC 于点 F,连接CM,CE.已知∠A=50°,∠ACE=30°.
求证:CE=CM;
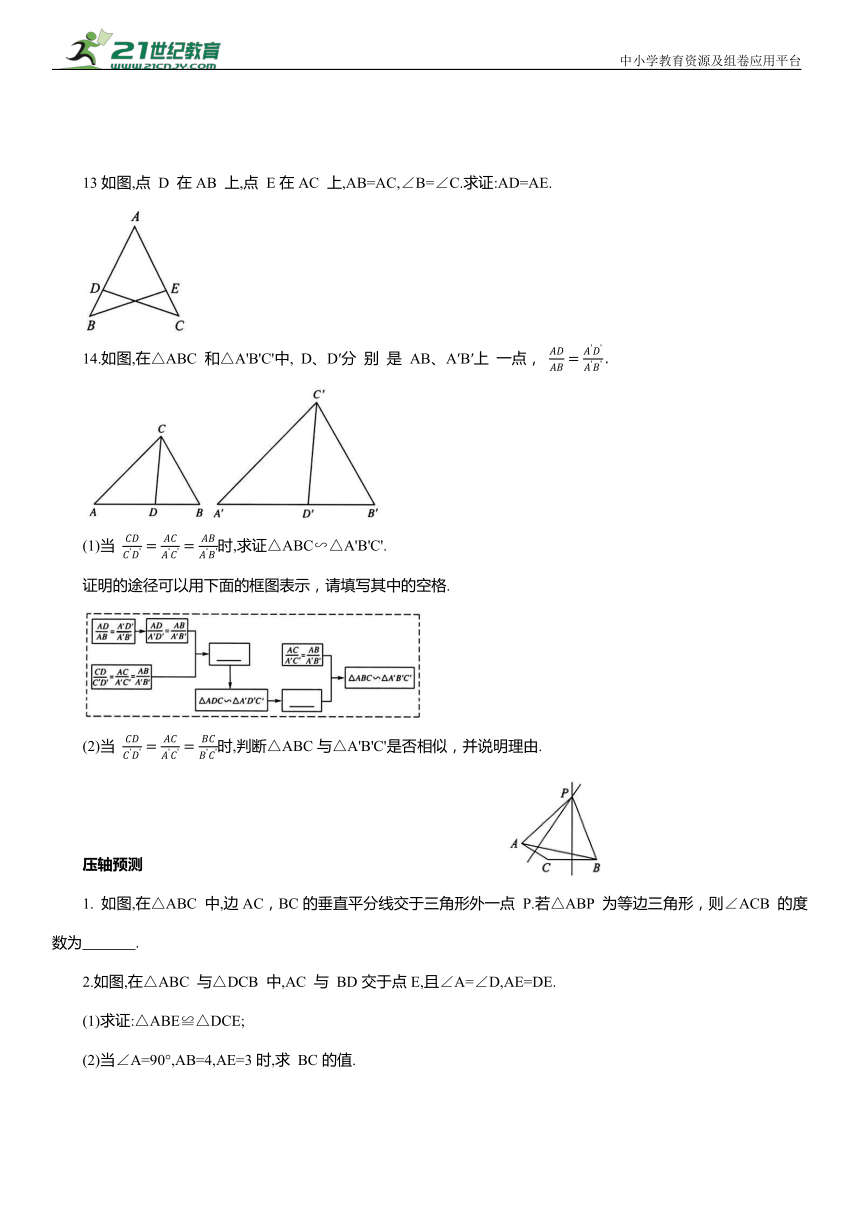
13如图,点 D 在AB 上,点 E在AC 上,AB=AC,∠B=∠C.求证:AD=AE.
14.如图,在△ABC 和△A'B'C'中, D、D′分 别 是 AB、A′B′上 一点,
(1)当 时,求证△ABC∽△A'B'C'.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当 时,判断△ABC与△A'B'C'是否相似,并说明理由.
压轴预测
1. 如图,在△ABC 中,边AC,BC的垂直平分线交于三角形外一点 P.若△ABP 为等边三角形,则∠ACB 的度数为 .
2.如图,在△ABC 与△DCB 中,AC 与 BD交于点E,且∠A=∠D,AE=DE.
(1)求证:△ABE≌△DCE;
(2)当∠A=90°,AB=4,AE=3时,求 BC的值.
3.如图,已知△ABC 中,AB=AC,点 D 是AC 上一点,BD=BC.
(1)求证:△ABC∽△BCD;
(2)若点 D 为 AC 中点,且 AC=4,求 BC的长.
4.已知:在△ABC 中,AB= AC,D 为 AC的中点,DE⊥AB,DF⊥BC,垂足分别为点 E,F,且DE=DF.求证:△ABC是等边三角形.
参考答案
1.(1)锐角 直角 钝角
(2)等腰 三边都不相等的
2.(1)大于 小于
(2)180° 与它不相邻的两内角的和
3.(1)两边
(2)平行 等于 一半
(3)线段
4.(1)相等
(2)高 中线 角平分线 重合 三线合一
(3)等腰三角形
5.(1)60°三线合一
(2)等边三角形 等边三角形等腰
6.(1)互余
(2)一半
(3)一半
(4)直角三角形中,两直角边的平方和等于斜边的平方
(5)若一个三角形中有两边的平方和等于第三边的平方,则这个三角形是直角三角形
7.(1)平行
(2)相似
(3)比例 夹角相等
(4)对应成比例
8.(1)成比例 相等
(2)中 高 相似 相似 相似比的平方
9.(1)对应边相等 对应角相等
(2)SSS SAS ASA AAS HL相等的边 夹角 对应边 另一组角 对应边 直角三角形
(3)对应边相等 对应角相等 相等相等 对应中线 对应角平分线
10.(1)综合法(由因导果)
(2)分析法(执果索因)
(3)两头凑法
1. B 【解析】本题考查三角形的高线.∵CD⊥AB,∴线段CD是△ABC的AB 边上的高线,故选 B.
2. B 【解析】本题考查平行线的性质、全等三角形的判定.∵AC∥DF,∴∠A=∠D.又AC=DF,若添加 AE=BD,则AE+BE=BD+BE,即 AB=DE,利用“SAS”可判定△ABC≌△DEF,故选 B.
3. B 【解析】本题考查相似三角形的判定与性质.因为 D,E分别为线段 BC,BA 的中点,所以 .所以△EBD∽△ABC,所以
故选 B.
4. C 【解析】本题考查角平分线的性质、等腰三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定与性质.∵∠DAE=∠CAB,∴∠DAC=∠EAB. 又AB=AC,AD = AE,∴△ADC≌△AEB,∴∠ADC=∠AEB,故选项 A 正确;∵∠CAB=36°,且 AB=AC,∴∠ABC=72°,∵BE平分∠ABC,∴∠ABG=∠CBG=∠DCA=36°,∴∠DCA=∠CAB,∴CD∥AB,故选项 B正确;DE=GE 条件不足,不能判定,故选项 C 错误;∵∠CBF=∠CAB=36°,且∠BCF=∠ACB,∴△CBF∽△CAB,则BCAC=CEB,∴BC=CF·AC. ∵ AB = AC,∠CAB= 36°, ∴∠ACB= 72°, ∴∠CFB= 180° -∠ACB-∠CBG=72°=∠ACB,∴BC= BF,∴BF =CF·AC,故选项 D正确,故选 C.
5. A 【解析】本题考查等边三角形的判定和性质、直角三角形的性质.∵∠ACB=90°,∠A =30°,∴∠B=60°.∵E是AB 的中点, 4=2,∴△BCE 为等边三角形.∵CD⊥AB,∴DE= 故选 A.
6. A 【解析】本题考查平行线分线段成比例、三角形的面积公式、勾股定理、平行线的判定和性质.如图,过点 A作AH⊥BC于 H.∵点 D 是AB 的中点,∴AD=BD. ∴DF∥AH, DF⊥DE,∴BF= HF, DF = AH.∵△DFE 的面积为1,∴ DE·DF=1,∴DE·DF=2,∴BC·AH=2DE·2DF=4×2=8,∴AB·AC=8. 解得AB=2(舍负),. 2 ,故选 A.
7.1 【解析】本题考查角平分线的性质、三角形的面积公式.如图,过点 D 作 DF⊥AC 于点 F.因为 AD 平分∠BAC,DE⊥AB,所以DF=DE=1,所以
8.40° 【解析】本题考查三角形内角和定理、线段垂直平分线的性质、三角形的外角性质.在 Rt△ABE中,∠B=90°,∠BAE=10°,∴∠AEB=80°.∵DE 是线段AC 的垂直平分线,∴AE=CE,∴∠C=∠CAE,∴∠AEB=∠CAE+∠C=2∠C=80°,∴∠C=40°.
9.54 【解析】本题考查等腰三角形的性质、三角形的外角性质、三角形的内角和定理. ∵ AF = EF,∴∠A=∠AEF.∵∠CFE=∠A+∠AEF,∴∠CFE=2∠A.又∵∠CFE=72°,∴∠A=36°,在 Rt△ABC 中,∠C=90°,∴∠A+∠B=90°,∴∠B=90°-∠A=54°.
10.82° 【解析】本题考查角平分线的定义、全等三角形的判定及性质、三角形的内角和定理.∵AC平分∠DCB,∴∠BCA=∠DCA.又∵CB=CD,AC=AC,∴△ABC≌△ADC(SAS),∴ ∠B = ∠D. ∵∠EAC= ∠D +∠DCA=49°,∴∠B+∠BCA=49°,∴∠BAE=180°- ,即∠BAE的度数为82°.
11.略
证明:∵BF=EC,
∴BF+CF=EC+CF,即 BC=EF.
在△ABC 和△DEF中
∴△ABC≌△DEF,
∴∠A=∠D.
12.略
根据直角三角形中线的性质、三角形内角和定理及三角形外角的性质得∠CME=∠CEM,即可得证.
解:证明:因为∠ACB=90°,点 M 为AB 的中点.
所以MA=MC,
所以∠MCA=∠A=50°,
所以∠CMA=180°-∠A-∠MCA=80°,
因为
所以∠CME=∠CEM,所以CE=CM.
13.略
根据已知条件,结合公共角,利用“ASA”即可判定△ACD≌△ABE,得对应边相等,从而证明AD=AE.
证明:在△ACD和△ABE中
∴△ACD≌△ABE.
∴AD=AE.
(2)相似,理由略
(1)根据比例式进行代换,得三边对应成比例,得两个三角形相似后,对应角相等,将所得三边比例式和对应角相等填入方框内;(2)分别在两个三角形中作 BC 边和B'C'边的平行线,利用所得三角形相似得比例式,再结合比例式进行代换,得三边对应成比例,证明△DCE∽△D'C'E',再利用平行线的性质,结合等角的补角相等以及两边对应成比例证明△ABC∽△A'B'C'.
解:
(2)如图,过点 D、D'分别作 DE∥BC、D'E'∥B'C',DE交AC 于点E,D'E'交A'C'于点 E'.
∵DE∥BC,∴△ADE∽△ABC.
同理
又
同理
即
∴△DCE∽△D'C'E'.
∴∠CED=∠C'E'D'.
∵DE∥BC,∴∠CED+∠ACB=180°.
同理
∴∠ACB=∠A'C'B'.
又AC=BC,∴△ABC∽△A'B'C'.
压轴预测
1.150° 【解析】本题考查线段垂直平分线的性质、等边三角形的性质、等腰三角形的性质、三角形的内角和定理.如图,连接 PC.设∠APC=x,∠BPC=y.∵△ABP是等边三角形,∴x+y=60°.∵点 P 是AC,BC 的垂直平分线的交点,∴PA=PC=PB,∴∠PAC=∠PCA,∠PCB=∠PBC.在等腰△PAC 中, 在等腰△PBC中, ∴∠ACB=∠PCA+∠PCB= ∴∠ACB的度数为150°.
2.(1)略
解:(1)证明:∵∠AEB与∠DEC是对顶角,
∴∠AEB=∠DEC.
又∵∠A=∠D,AE=DE,
∴△ABE≌△DCE(ASA).
(2)∵∠A=90°,∴在 Rt△ABE中,
∵△ABE≌△DCE,
∴CE=BE=5,
∴AC=AE+CE=3+5=8,
故在 Rt△ABC中,
3.(1)略 (2)2
(1)根据等边对等角得两组角相等,即可证明两个三角形相似;(2)根据相似三角形的对应边成比例得比例式,将线段的长代入比例式,从而即可求出 BC的长.
解:(1)证明:∵AB=AC,
∴∠ABC=∠C.
又BD=BC,
∴∠BDC=∠C,
∴∠ABC=∠C=∠BDC,
∴∠BAC=∠CBD,
∴△ABC∽△BCD.
(2)由(1)△ABC∽△BCD得
又AC=4,D为AC中点,
∴CD=2,
又BC>0,
4.略
证明:∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°.
∵点 D为AC 的中点,
∴AD=DC.
在 Rt△ADE 和 Rt△CDF中,
∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,∴AB=BC.
∵AB=AC,∴AB=BC=AC,
∴△ABC是等边三角形.
专题 10 三角形
1.三角形的分类
(1)三角形按角分为 三角形、 三角形、 三角形.
(2)三角形按边分为 三角形、 三角形.
2.三角形的性质
(1)三角形中任意两边之和 第三边,任意两边之差 第三边.
(2)三角形的内角和为 ,外角与内角的关系:三角形的外角等于
3.三角形中的主要线段
(1)连接三角形 中点的线段叫作三角形的中位线.
(2)中位线的性质:三角形的中位线 于第三边,并且 第三边的 .
(3) 三角形的中线、高线、角平分线都是 .
4.等腰三角形的性质与判定
(1)等腰三角形的两底角 .
(2)等腰三角形底边上的 、底边上的 、顶角的 互 相 ,简称“ ”.
(3)有两个角相等的三角形是 .
5.等边三角形的性质与判定
(1)等边三角形每个角都等于 ,同样具有“ ”的性质.
(2)三个角相等的三角形是 ,三边相等的三角形是 ,一个角等于 60°的 三角形是等边三角形.
6.直角三角形的性质与判定
(1)直角三角形两锐角 .
(2)直角三角形中 30°所对的直角边等于斜边的 .
(3)直角三角形中,斜边的中线等于斜边的 .
(4)勾股定理:
(5)勾股定理的逆定理: ·
7.相似三角形的判定方法有:
(1) 于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;
(2)两个角对应相等的两个三角形 ;
(3)两边对应成 且 的两个三角形相似;
(4)三边 的两个三角形相似.
8.相似三角形的性质有:(1)相似三角形的对应边 ,对应角 ;(2)相似三角形的对应边的 线、对应边上的 的比等于 比,周长之比也等于 比,面积比等于 .
9.全等三角形
(1)全等三角形: 、 的三角形叫作全等三角形.
(2) 三角 形 全 等 的 判 定 方 法 有: 、 、 、 、 .在证明两个三角形全等时,选择三角形全等的五种方法中,至少有一组 ,因此在应用时要养成先找边的习惯.如果选择找到了一组对应边,再找第二组条件:若找到一组对应边则再找这两边的 用“SAS”或再找第三组 用“SSS”;若找到一组角则需找 (可能用“ASA”或“AAS”)或夹这个角的另一组 用“SAS”;若是判定两个 全等则优先考虑“HL”.
(3)全等三角形的性质:全等三角形的 、 ,全等三角形的面积 、周长 、对应高、 、 相等.
10.分析、证明几何题的常用方法
(1) :从命题的题设出发,通过一系列的有关定义、公理、定理的运用,逐步向前推进,直到问题解决.(2) :从命题的结论出发,不断寻找使结论成立的条件,直到已知条件.(3) :将分析法与综合法合并使用,比较起来,分析法利于思考,综合法宜于表达,因此在实际思考问题时,可合并使用灵活处理,以利于缩短题设与结论之间的距离,最后达到完全沟通.
实战演练
1.如图,CD⊥AB 于点 D,已知∠ABC是钝角,则 ( )
A.线段CD是△ABC的AC 边上的高线
B.线段 CD 是△ABC的AB 边上的高线
C.线段 AD 是△ABC的BC 边上的高线
D.线段 AD 是△ABC的AC 边上的高线
2.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF 的是 ( )
A. BC=DE B. AE=DB
C.∠A=∠DEF D.∠ABC=∠D
3.如图,在△ABC中,D、E分别为线段 BC、BA 的中点,设△ABC 的面积为S ,△EBD的面积为S ,则
A. B. C. D.
4.如图, 在 △ABC 和△ADE 中,∠CAB=∠DAE= 36°,AB =AC,AD=AE.连接CD,连接 BE 并延长交AC,AD 于点 F,G.若 BE 恰好平分∠ABC,则下列结论错误的是 ( )
A.∠ADC=∠AEB B. CD∥AB
C. DE=GE D. BF =CF·AC
5. 如图,在 Rt△ABC 中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E 是AB 的中点,则 DE的长为 ( )
A.1 B.2 C.3 D.4
6.如图,在△ABC 中,∠A=90°,D 是AB 的中点,过点 D 作 BC 的平行线交AC 于点 E,作 BC的垂线交 BC 于点 F,若AB=CE,且△DFE 的面积为1,则 BC的长为 ( )
A.2 B.5
D.10
7.如图,在△ABC中,AD 平分∠BAC,DE⊥AB.若 AC=2,DE=1,则S△ACD= .
8. 如图,在 Rt△ABC中,∠ABC=90°,ED是AC 的垂直平分线,交AC 于点D,交 BC 于点 E,∠BAE=10°,则∠C的度数是 .
9.如图,在 Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= °.
10如图,AC 平 分 ∠DCB,CB=CD,DA 的延长线交BC 于点 E,若∠EAC = 49°, 则 ∠BAE 的 度 数为
11.如图,点 B,F,C,E 在同一条 直 线 上, BF = EC, AB = DE,∠B=∠E.
求证:∠A=∠D.
12.如图,在 Rt△ACB中,∠ACB=90°,点 M 为边AB 的中点,点 E在线段 AM 上,EF⊥AC 于点 F,连接CM,CE.已知∠A=50°,∠ACE=30°.
求证:CE=CM;
13如图,点 D 在AB 上,点 E在AC 上,AB=AC,∠B=∠C.求证:AD=AE.
14.如图,在△ABC 和△A'B'C'中, D、D′分 别 是 AB、A′B′上 一点,
(1)当 时,求证△ABC∽△A'B'C'.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当 时,判断△ABC与△A'B'C'是否相似,并说明理由.
压轴预测
1. 如图,在△ABC 中,边AC,BC的垂直平分线交于三角形外一点 P.若△ABP 为等边三角形,则∠ACB 的度数为 .
2.如图,在△ABC 与△DCB 中,AC 与 BD交于点E,且∠A=∠D,AE=DE.
(1)求证:△ABE≌△DCE;
(2)当∠A=90°,AB=4,AE=3时,求 BC的值.
3.如图,已知△ABC 中,AB=AC,点 D 是AC 上一点,BD=BC.
(1)求证:△ABC∽△BCD;
(2)若点 D 为 AC 中点,且 AC=4,求 BC的长.
4.已知:在△ABC 中,AB= AC,D 为 AC的中点,DE⊥AB,DF⊥BC,垂足分别为点 E,F,且DE=DF.求证:△ABC是等边三角形.
参考答案
1.(1)锐角 直角 钝角
(2)等腰 三边都不相等的
2.(1)大于 小于
(2)180° 与它不相邻的两内角的和
3.(1)两边
(2)平行 等于 一半
(3)线段
4.(1)相等
(2)高 中线 角平分线 重合 三线合一
(3)等腰三角形
5.(1)60°三线合一
(2)等边三角形 等边三角形等腰
6.(1)互余
(2)一半
(3)一半
(4)直角三角形中,两直角边的平方和等于斜边的平方
(5)若一个三角形中有两边的平方和等于第三边的平方,则这个三角形是直角三角形
7.(1)平行
(2)相似
(3)比例 夹角相等
(4)对应成比例
8.(1)成比例 相等
(2)中 高 相似 相似 相似比的平方
9.(1)对应边相等 对应角相等
(2)SSS SAS ASA AAS HL相等的边 夹角 对应边 另一组角 对应边 直角三角形
(3)对应边相等 对应角相等 相等相等 对应中线 对应角平分线
10.(1)综合法(由因导果)
(2)分析法(执果索因)
(3)两头凑法
1. B 【解析】本题考查三角形的高线.∵CD⊥AB,∴线段CD是△ABC的AB 边上的高线,故选 B.
2. B 【解析】本题考查平行线的性质、全等三角形的判定.∵AC∥DF,∴∠A=∠D.又AC=DF,若添加 AE=BD,则AE+BE=BD+BE,即 AB=DE,利用“SAS”可判定△ABC≌△DEF,故选 B.
3. B 【解析】本题考查相似三角形的判定与性质.因为 D,E分别为线段 BC,BA 的中点,所以 .所以△EBD∽△ABC,所以
故选 B.
4. C 【解析】本题考查角平分线的性质、等腰三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定与性质.∵∠DAE=∠CAB,∴∠DAC=∠EAB. 又AB=AC,AD = AE,∴△ADC≌△AEB,∴∠ADC=∠AEB,故选项 A 正确;∵∠CAB=36°,且 AB=AC,∴∠ABC=72°,∵BE平分∠ABC,∴∠ABG=∠CBG=∠DCA=36°,∴∠DCA=∠CAB,∴CD∥AB,故选项 B正确;DE=GE 条件不足,不能判定,故选项 C 错误;∵∠CBF=∠CAB=36°,且∠BCF=∠ACB,∴△CBF∽△CAB,则BCAC=CEB,∴BC=CF·AC. ∵ AB = AC,∠CAB= 36°, ∴∠ACB= 72°, ∴∠CFB= 180° -∠ACB-∠CBG=72°=∠ACB,∴BC= BF,∴BF =CF·AC,故选项 D正确,故选 C.
5. A 【解析】本题考查等边三角形的判定和性质、直角三角形的性质.∵∠ACB=90°,∠A =30°,∴∠B=60°.∵E是AB 的中点, 4=2,∴△BCE 为等边三角形.∵CD⊥AB,∴DE= 故选 A.
6. A 【解析】本题考查平行线分线段成比例、三角形的面积公式、勾股定理、平行线的判定和性质.如图,过点 A作AH⊥BC于 H.∵点 D 是AB 的中点,∴AD=BD. ∴DF∥AH, DF⊥DE,∴BF= HF, DF = AH.∵△DFE 的面积为1,∴ DE·DF=1,∴DE·DF=2,∴BC·AH=2DE·2DF=4×2=8,∴AB·AC=8. 解得AB=2(舍负),. 2 ,故选 A.
7.1 【解析】本题考查角平分线的性质、三角形的面积公式.如图,过点 D 作 DF⊥AC 于点 F.因为 AD 平分∠BAC,DE⊥AB,所以DF=DE=1,所以
8.40° 【解析】本题考查三角形内角和定理、线段垂直平分线的性质、三角形的外角性质.在 Rt△ABE中,∠B=90°,∠BAE=10°,∴∠AEB=80°.∵DE 是线段AC 的垂直平分线,∴AE=CE,∴∠C=∠CAE,∴∠AEB=∠CAE+∠C=2∠C=80°,∴∠C=40°.
9.54 【解析】本题考查等腰三角形的性质、三角形的外角性质、三角形的内角和定理. ∵ AF = EF,∴∠A=∠AEF.∵∠CFE=∠A+∠AEF,∴∠CFE=2∠A.又∵∠CFE=72°,∴∠A=36°,在 Rt△ABC 中,∠C=90°,∴∠A+∠B=90°,∴∠B=90°-∠A=54°.
10.82° 【解析】本题考查角平分线的定义、全等三角形的判定及性质、三角形的内角和定理.∵AC平分∠DCB,∴∠BCA=∠DCA.又∵CB=CD,AC=AC,∴△ABC≌△ADC(SAS),∴ ∠B = ∠D. ∵∠EAC= ∠D +∠DCA=49°,∴∠B+∠BCA=49°,∴∠BAE=180°- ,即∠BAE的度数为82°.
11.略
证明:∵BF=EC,
∴BF+CF=EC+CF,即 BC=EF.
在△ABC 和△DEF中
∴△ABC≌△DEF,
∴∠A=∠D.
12.略
根据直角三角形中线的性质、三角形内角和定理及三角形外角的性质得∠CME=∠CEM,即可得证.
解:证明:因为∠ACB=90°,点 M 为AB 的中点.
所以MA=MC,
所以∠MCA=∠A=50°,
所以∠CMA=180°-∠A-∠MCA=80°,
因为
所以∠CME=∠CEM,所以CE=CM.
13.略
根据已知条件,结合公共角,利用“ASA”即可判定△ACD≌△ABE,得对应边相等,从而证明AD=AE.
证明:在△ACD和△ABE中
∴△ACD≌△ABE.
∴AD=AE.
(2)相似,理由略
(1)根据比例式进行代换,得三边对应成比例,得两个三角形相似后,对应角相等,将所得三边比例式和对应角相等填入方框内;(2)分别在两个三角形中作 BC 边和B'C'边的平行线,利用所得三角形相似得比例式,再结合比例式进行代换,得三边对应成比例,证明△DCE∽△D'C'E',再利用平行线的性质,结合等角的补角相等以及两边对应成比例证明△ABC∽△A'B'C'.
解:
(2)如图,过点 D、D'分别作 DE∥BC、D'E'∥B'C',DE交AC 于点E,D'E'交A'C'于点 E'.
∵DE∥BC,∴△ADE∽△ABC.
同理
又
同理
即
∴△DCE∽△D'C'E'.
∴∠CED=∠C'E'D'.
∵DE∥BC,∴∠CED+∠ACB=180°.
同理
∴∠ACB=∠A'C'B'.
又AC=BC,∴△ABC∽△A'B'C'.
压轴预测
1.150° 【解析】本题考查线段垂直平分线的性质、等边三角形的性质、等腰三角形的性质、三角形的内角和定理.如图,连接 PC.设∠APC=x,∠BPC=y.∵△ABP是等边三角形,∴x+y=60°.∵点 P 是AC,BC 的垂直平分线的交点,∴PA=PC=PB,∴∠PAC=∠PCA,∠PCB=∠PBC.在等腰△PAC 中, 在等腰△PBC中, ∴∠ACB=∠PCA+∠PCB= ∴∠ACB的度数为150°.
2.(1)略
解:(1)证明:∵∠AEB与∠DEC是对顶角,
∴∠AEB=∠DEC.
又∵∠A=∠D,AE=DE,
∴△ABE≌△DCE(ASA).
(2)∵∠A=90°,∴在 Rt△ABE中,
∵△ABE≌△DCE,
∴CE=BE=5,
∴AC=AE+CE=3+5=8,
故在 Rt△ABC中,
3.(1)略 (2)2
(1)根据等边对等角得两组角相等,即可证明两个三角形相似;(2)根据相似三角形的对应边成比例得比例式,将线段的长代入比例式,从而即可求出 BC的长.
解:(1)证明:∵AB=AC,
∴∠ABC=∠C.
又BD=BC,
∴∠BDC=∠C,
∴∠ABC=∠C=∠BDC,
∴∠BAC=∠CBD,
∴△ABC∽△BCD.
(2)由(1)△ABC∽△BCD得
又AC=4,D为AC中点,
∴CD=2,
又BC>0,
4.略
证明:∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°.
∵点 D为AC 的中点,
∴AD=DC.
在 Rt△ADE 和 Rt△CDF中,
∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,∴AB=BC.
∵AB=AC,∴AB=BC=AC,
∴△ABC是等边三角形.
同课章节目录
