专题14 解直角三角形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 专题14 解直角三角形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 443.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
专题14 解直角三角形
1.锐角三角函数的定义
如图,在△ABC中,∠C=90°.
(1)锐角 A 的对边与斜边的比叫作∠A的正弦,记为 sinA,即 sinA= .
(2)锐角 A 的邻边与斜边的比叫作∠A的余弦,记为 cosA,即 cosA= .
(3)锐角 A 的对边与邻边的比叫作∠A的正切,记为 tanA,即 tanA= .
2.一些特殊角的三角函数值
α 三角函数 0° 30° 45° 60° 90°
sinα
cosα
tanα
3.各锐角三角函数之间的关系
(1) 互 余 关 系: sinA = ,cosA= .
(2)推导关系: tanA= .
4.解直角三角形的概念
在直角三角形中,除直角外,一共有五个元素,即三个 和两个 .由直角三角形中除直角外的已知元素求出所有其他元素的过程叫作解直角三角形.解直角三角形的理论依据:在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)三边之间的关系: .
(2)锐角之间的关系: .
(3)边角之间的关系:
sinA = , cosA = ,tanA= ;
sinB = , cosB = ,tanB= .
5.了解测量等实际问题中的概念
(1)方位角从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为 .
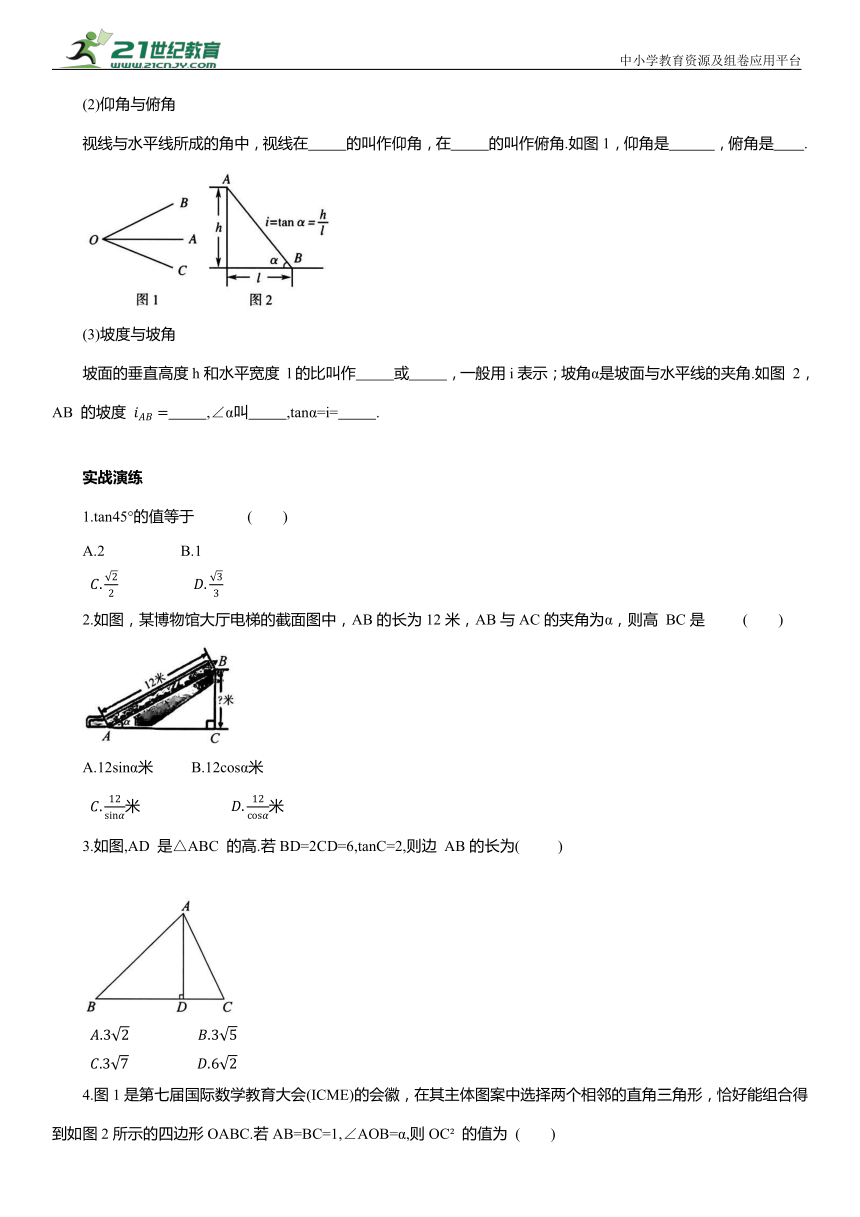
(2)仰角与俯角
视线与水平线所成的角中,视线在 的叫作仰角,在 的叫作俯角.如图1,仰角是 ,俯角是 .
(3)坡度与坡角
坡面的垂直高度h和水平宽度 l的比叫作 或 ,一般用i表示;坡角α是坡面与水平线的夹角.如图 2,AB 的坡度 ,∠α叫 ,tanα=i= .
实战演练
1.tan45°的值等于 ( )
A.2 B.1
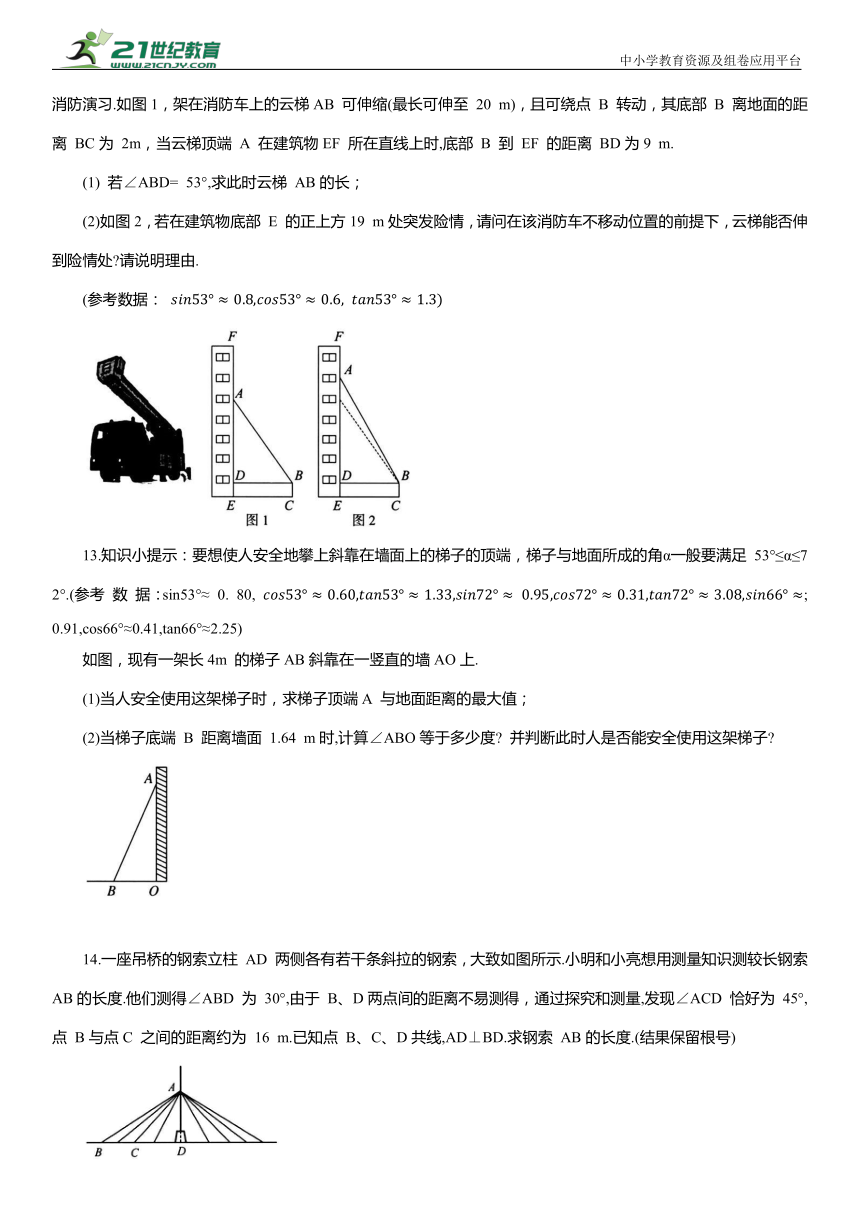
2.如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高 BC是 ( )
A.12sinα米 B.12cosα米
米 米
3.如图,AD 是△ABC 的高.若BD=2CD=6,tanC=2,则边 AB的长为( )
4.图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=1,∠AOB=α,则OC 的值为 ( )
5.如图,小明想要测量学校操场上旗杆 AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为 ( )
A. a+btanα
B. a+bsinα
6.如图,沿 AB 方向架桥修路,为加快施工进度,在直线 AB 上湖的另一边的 D 处同时施工. 取∠ABC= 150°,BC=1 600m,∠BCD=105°,则C,D 两点的距离是 m.
7.如图,有甲乙两座建筑物,从甲建筑物 A 点处测得乙建筑物 D 点的俯角α为 45°,C点的俯角β为58°,BC为两座建筑物的水平距离.已知乙建筑物的高度CD为6m ,则甲建筑物的高度 AB为 m. 0.53,tan58°≈1.60,结果保留整数)
8.如图,海中有一个小岛 A.一艘轮船由西向东航行,在B 点测得小岛 A 在北偏东 60°方向上;航行12n mile到达 C 点,这时测得小岛 A 在北偏东30°方向上.小岛A 到航线 BC 的距离是 n mile ,结果用四舍五入法精确到0.1).
9.一条上山直道的坡度为1:7,沿这条直道上山,每前进 100 米所上升的高度为 米.
10.2022 年 6 月 6 日是第27 个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.
如图,当张角∠AOB=150°时,顶部边缘A 处离桌面的高度AC 的长为 10 cm,此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角∠A'OB=108°时(点 A′是A的对应点),用眼舒适度较为理想.求此时顶部边缘 A'处离桌面的高度 A'D的长.(结果精确到 1 cm;参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
11.湖中小岛上码头 C处一名游客突发疾病,需要救援.位于湖面 B 点处的快艇和湖岸A 处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头 C 接该游客,再沿 CA 方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A 的北偏东30°方向上,B在A 的北偏东60°方向上,且在 C 的正南方向 900米处.
(1)求湖岸 A 与码头C 的距离(结果精确到 1 米,参考数据:
(2)救援船的平均速度为150米/分,快艇的平均速度为400 米/分.在接到通知后,快艇能否在 5分钟内将该游客送上救援船 请说明理由.(接送游客上下船的时间忽略不计)
12.每年的11 月 9 日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB 可伸缩(最长可伸至 20 m),且可绕点 B 转动,其底部 B 离地面的距离 BC为 2m,当云梯顶端 A 在建筑物EF 所在直线上时,底部 B 到 EF 的距离 BD为9 m.
(1) 若∠ABD= 53°,求此时云梯 AB的长;
(2)如图2,若在建筑物底部 E 的正上方19 m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处 请说明理由.
(参考数据:
13.知识小提示:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足 53°≤α≤72°.(参考 数 据:sin53°≈ 0. 80, ;0.91,cos66°≈0.41,tan66°≈2.25)
如图,现有一架长4m 的梯子AB斜靠在一竖直的墙AO上.
(1)当人安全使用这架梯子时,求梯子顶端A 与地面距离的最大值;
(2)当梯子底端 B 距离墙面 1.64 m时,计算∠ABO等于多少度 并判断此时人是否能安全使用这架梯子
14.一座吊桥的钢索立柱 AD 两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得∠ABD 为 30°,由于 B、D两点间的距离不易测得,通过探究和测量,发现∠ACD 恰好为 45°,点 B与点C 之间的距离约为 16 m.已知点 B、C、D共线,AD⊥BD.求钢索 AB的长度.(结果保留根号)
15.拓展小组研制的智能操作机器人,如图 1,水平操作台为 l,底座AB 固定,高 AB 为 50cm,连杆 BC长度为70 cm,手臂CD长度为60 cm.点 B,C是转动点,且 AB,BC与CD 始终在同一平面内.
(1)转动连杆 BC,手臂 CD,使∠ABC=143°,CD∥l,如图2,求手臂端点 D 离操作台l 的高度 DE 的长(精确到 1 cm,参考数据:
(2)物品在操作台 l 上,距离底座 A 端110 cm 的点 M 处,转动连杆 BC,手臂CD,手臂端点 D 能否碰到点 M 请说明理由.
压轴预测
1.如图,Rt△ABC 中,∠BAC=90°,AD⊥BC于点D,若 AD: CD=4: 3,则 tanB的值为 ( )
A. B.
C. D.
2.某公园有一座古塔,古塔前有一个斜坡CD,坡角 ∠DCE = 42°, 斜坡高 DE =1.8米,DQ是平行于水平地面BC 的一个平台.小华想利用所学知识测量古塔的高度 AB,她在平台的点 G 处水平放置一平面镜,她沿着GQ方向移动,当移动到点 N时,刚好在镜面中看到古塔顶端点 A 的像,这时,测得小华眼睛与地面的距离MN= 1.5 米,GN=2 米,BC=16 米,DG=8米,已知 AB⊥BC,MN⊥DQ,根据题中提供的相关信息,古塔的高度 AB 约为(参考数据:sin42°≈0. 67, cos42°≈0.74,tan42°≈0.90) ( )
A.19.5米
B.19.7米
C.21.3米
D.22.1米
3.如图,C 岛在A 岛的北偏东45°方向,在 B岛的北偏西25°方向.
(1)直接写出∠ACB的度数是 ;
(2)测量发现∠BAC=20°,A 岛与C 岛之间的距离AC=20海里,求 A 岛与 B 岛之间的距离.(结果精确到0.1海里)(参考数据: 0.36)
4.某地为了让山顶通电,需要从山脚点 B 开始接驳电线,经过中转站 D,再连通到山顶点 A 处,测得山顶 A 的 高 度 AC 为300米,从山脚 B 到山顶 A 的水平距离BC 是500 米,斜面BD 的坡度i=1:2(指DF 与BF 的比),从点 D 看向点A 的仰角为 45°.
(1)斜面 AD的坡度i= ;
(2)求电线 AD+BD 的长度(结果保留根号).
参考答案
2.
4.边 角
(2)互余
(3)
5.(1)方位角
(2)水平线上方 水平线下方 ∠AOB∠AOC
(3)坡度 坡比 hl 坡角 hl
1. B 【解析】本题考查特殊角的三角函数值.tan45°=1,故选 B.
2. A 【解析】本题考查解直角三角形的实际应用.在Rt△ABC中,∠ACB=90°,所以 所以BC=12sinα米,故选 A.
3. D 【解析】本题考查解直角三角形.∵BD=2CD=6,
∴CD=3.∵tanC=2,AD 是△ABC 的高, ∴AD=6.在 Rt△ABD中,. 故选 D.
4. A 【解析】本题考查三角函数的应用、勾股定理.由题意得 则 由勾股定理得( 故选 A.
5. A 【解析】本题考查三角函数的实际应用.过点C作CF⊥AB于点 F,由题意得CF=DB=b,∵tan∠ACF=AF,∴AF=tan∠ACF×CF= btana,∴AB=AF+FB=AF+CD=a+btanα,故选 A.
【解析】本题考查解直角三角形.如图,过点C作CE⊥BD 于点 E.∵∠ABC=150°,∠BCD=105°, 1 6(
7.16 【解析】本题考查解直角三角形的实际应用.如图,过点 D作 DH⊥AB 于点 H ,易知四边形 BCDH 为矩形,则DH=BC,BH=CD=6m .由平行线的性质可知∠ADH=α=45°,∠ACB=β=58°.在 Rt△ADH 中,设AH= xm,则 DH= xm,所以 BC= xm,AB=AH+BH=(x+6)m.在 Rt△ABC 中,tan∠ACB= tan58°= 解得x≈10,则甲建筑物的高度 AB约为16 m.
8.10.4 【解析】本题考查解直角三角形的实际应用.作AD⊥BC于点 D,则∠ABC=30°,∠ACD=60°,∠BAC=30°.设CD=a,在 Rt△ACD中,AD= a,AC=BC=2a=12,
【解析】本题考查解直角三角形的应用.设上升的高度为x米,∵上山直道的坡度为1:7,∴水平距离为7x米,由勾股定理得 解得 (舍去),∴每前进 100 米所上升的高度为10 米.
10.19 cm
先在 Rt△AOC中,求出 AO的长,再在 Rt△A'OD 中,利用锐角三角函数即可求出 A'D的长.
解:由题意可知,
在 Rt△AOC中, AC=10 cm,
∴AO=2AC=20cm.
在 Rt△A'OD 中, A'O=AO=20cm,
即顶部边缘 A'处离桌面的高度A'D 的长约为 19 cm.
11.(1)1 559 米 (2)能,理由略
(1)过点 A 作AD⊥CB,交CB的延长线于点D,根据题意可得∠CAB,∠BAD的度数,再由平行线的性质及等腰三角形的判定可得AB,BD的长,进而得 CD的长,结合锐角三角函数的定义即可求出答案;(2)分别求出快艇和救援船5分钟内行驶的路程和以及实际行驶的路程和,进行比较即可得解.
解:(1)如图,过点 A 作AD⊥CB,交 CB 的延长线于点 D,则∠ADC=90°.
由题意得∠NAC=30°,∠NAB=60°.
∴∠CAB=30°,∠BAD=30°.
∵NA∥CB,
∴∠C=∠NAC=30°.
∴AB=BC=900.∴BD=450.
∴CD=900+450=1350.
∵在 Rt△ACD中.
答:湖岸 A 与码头C 的距离约为 1 559 米.
(2)在接到通知后,快艇能在5分钟内将该游客送上救援船.理由如下:
快艇和救援船5分钟一共可行驶的路程为
5×150+5×400=2750,
快艇和救援船实际行驶的路程和为
1559+900=2459.
∵2750>2459,
∴在接到通知后,快艇能在5分钟内将该游客送上救援船.
12.(1)15 m (2)能,理由略
(1)在 Rt△ABD 中,利用锐角三角函数即可求解;
(2)结合已知条件先求出AD的长,再利用勾股定理求出 AB的长,比较大小即可作出判断.
解:(1)在 Rt△ABD中,∠ABD=53°,BD=9,
答:此时云梯AB的长为15 m.
(2)∵AE=19,BC=2,
∴AD=19-2=17.
在Rt△ABD中,BD=9,
∴在该消防车不移动位置的前提下,云梯能够伸到险情处.
13.(1)3.8 米 (2)∠ABO=66°,能
(1)根据α的取值范围,确定 AO取最大值时所对应α的值,在 Rt△AOB中,由正弦的定义即可求解;(2)在Rt△AOB 中,由余弦的定义求出 cos∠ABO,再结合已知条件求出∠ABO,即可判断.
解: ,当α=72°时,AO取最大值.
在 Rt△AOB中,
∴AO=ABsin∠ABO
=4sin72°
=4×0.95
=3.8,
所以梯子顶端A 与地面的距离的最大值3.8米.
(2)在 Rt△AOB 中.
cos∠ABO=1.64÷4=0.41,cos66°≈0.41,
∴∠ABO=66°.
∴人能安全使用这架梯子.
设AD=x,根据三角函数构造关于 AD的方程,解方程进而求得AB.
解:解法一:在△ADC中,设AD=x.
∵AD⊥BD,∠ACD=45°,
∴CD=AD=x.
在△ADB中,AD⊥BD,∠ABD=30°,
∴AD=BDtan30°,
即
解之,得
∴钢索 AB 的长度约为(
解法二:在△ADB中,设AB=x.
∵AD⊥BD,∠ABD=30°,
在△ADC中,AD⊥BD,∠ACD=45°,
∴AD=CD,
即
解之,得
∴钢索 AB的长度约为(
15.(1)106 cm (2)能,理由略
(1)作CP⊥AE于点 P,BQ⊥CP 于点 Q,由 CQ+PQ计算CP 得到DE 即可;(2)根据题意画出图形,根据图形运用勾股定理求解 AD,从而即可判断.
解:(1)过点C作CP⊥AE于点 P,
过点 B作 BQ⊥CP 于点 Q,如图1,
∵∠ABC=143°,∴∠CBQ=53°,
∴在 Rt△BCQ中,
∵CD∥l,∴DE=CP=CQ+PQ=56+50=106 cm.
(2)当点 B,C,D共线时,如图2,
BD=60+70=130cm,AB=50cm,
在 Rt△ABD中,
∴AD=120 cm>110 cm.
∴手臂端点 D能碰到点 M.
压轴预测
1. C 【解析】本题考查锐角三角函数. ∵AD⊥BC,∴∠ADB=∠ADC= 90°. 又∠BAC= 90°,∴∠B +∠BAD=∠BAD+∠CAD = 90°,∴∠B=∠CAD, 故选C.
2. C 【解析】本题考查解直角三角形及相似三角形的应用.在 Rt△CDE 中, ∴CE≈2(米).延长 GD 交 AB 于点 H,则 BH=DE=1.8(米),DH=BE=BC+CE≈18(米),HG=DH+DG≈26(米).∵∠AHG=∠MNG= 90°,∠AGH=∠MGN,∴△AHG∽△MNG,∴AH:MN=HG:NG,即AH:1.5=26:2,∴AH=19.5(米),∴AB=AH+HB=21.3(米),故选 C.
中小学教育资源及组卷应用平台
3.(1)70° (2)18.8海里
(1)根据已知方位角的度数即可求解;(2)根据∠BAC的度数求出∠CBA的度数,在直角三角形中利用锐角的三角函数即可求出AB的距离.
解:(1)70°.
(2)当∠BAC=20°时,∠CBA=90°,
∴AB=AC×cos∠BAC=AC×cos20°
≈20×0.94=18.8(海里).
4.(1)1:1( 米
(1)根据斜面 AD 的坡度i=AE:DE 即可求解;(2)设AE=x,EC=y,利用斜面 BD的坡度表示出BF,在根据已知条件建立关于x和y的方程组,解方程组即可求出x和y的值,再根据勾股定理求出 BD,AD的长,相加即可求解.
解:(1)1:1.
(2)设AE=x,EC=y,
∴FC=DE=AE=x,DF=EC=y.
∵斜面 BD的坡度i=DF:BF=1:2,∴BF=2y.
依题意得 解得
根据勾股定理得
答:电线AD+BD的长度为( 米.
1.锐角三角函数的定义
如图,在△ABC中,∠C=90°.
(1)锐角 A 的对边与斜边的比叫作∠A的正弦,记为 sinA,即 sinA= .
(2)锐角 A 的邻边与斜边的比叫作∠A的余弦,记为 cosA,即 cosA= .
(3)锐角 A 的对边与邻边的比叫作∠A的正切,记为 tanA,即 tanA= .
2.一些特殊角的三角函数值
α 三角函数 0° 30° 45° 60° 90°
sinα
cosα
tanα
3.各锐角三角函数之间的关系
(1) 互 余 关 系: sinA = ,cosA= .
(2)推导关系: tanA= .
4.解直角三角形的概念
在直角三角形中,除直角外,一共有五个元素,即三个 和两个 .由直角三角形中除直角外的已知元素求出所有其他元素的过程叫作解直角三角形.解直角三角形的理论依据:在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)三边之间的关系: .
(2)锐角之间的关系: .
(3)边角之间的关系:
sinA = , cosA = ,tanA= ;
sinB = , cosB = ,tanB= .
5.了解测量等实际问题中的概念
(1)方位角从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为 .
(2)仰角与俯角
视线与水平线所成的角中,视线在 的叫作仰角,在 的叫作俯角.如图1,仰角是 ,俯角是 .
(3)坡度与坡角
坡面的垂直高度h和水平宽度 l的比叫作 或 ,一般用i表示;坡角α是坡面与水平线的夹角.如图 2,AB 的坡度 ,∠α叫 ,tanα=i= .
实战演练
1.tan45°的值等于 ( )
A.2 B.1
2.如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高 BC是 ( )
A.12sinα米 B.12cosα米
米 米
3.如图,AD 是△ABC 的高.若BD=2CD=6,tanC=2,则边 AB的长为( )
4.图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=1,∠AOB=α,则OC 的值为 ( )
5.如图,小明想要测量学校操场上旗杆 AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为 ( )
A. a+btanα
B. a+bsinα
6.如图,沿 AB 方向架桥修路,为加快施工进度,在直线 AB 上湖的另一边的 D 处同时施工. 取∠ABC= 150°,BC=1 600m,∠BCD=105°,则C,D 两点的距离是 m.
7.如图,有甲乙两座建筑物,从甲建筑物 A 点处测得乙建筑物 D 点的俯角α为 45°,C点的俯角β为58°,BC为两座建筑物的水平距离.已知乙建筑物的高度CD为6m ,则甲建筑物的高度 AB为 m. 0.53,tan58°≈1.60,结果保留整数)
8.如图,海中有一个小岛 A.一艘轮船由西向东航行,在B 点测得小岛 A 在北偏东 60°方向上;航行12n mile到达 C 点,这时测得小岛 A 在北偏东30°方向上.小岛A 到航线 BC 的距离是 n mile ,结果用四舍五入法精确到0.1).
9.一条上山直道的坡度为1:7,沿这条直道上山,每前进 100 米所上升的高度为 米.
10.2022 年 6 月 6 日是第27 个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.
如图,当张角∠AOB=150°时,顶部边缘A 处离桌面的高度AC 的长为 10 cm,此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角∠A'OB=108°时(点 A′是A的对应点),用眼舒适度较为理想.求此时顶部边缘 A'处离桌面的高度 A'D的长.(结果精确到 1 cm;参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
11.湖中小岛上码头 C处一名游客突发疾病,需要救援.位于湖面 B 点处的快艇和湖岸A 处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头 C 接该游客,再沿 CA 方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A 的北偏东30°方向上,B在A 的北偏东60°方向上,且在 C 的正南方向 900米处.
(1)求湖岸 A 与码头C 的距离(结果精确到 1 米,参考数据:
(2)救援船的平均速度为150米/分,快艇的平均速度为400 米/分.在接到通知后,快艇能否在 5分钟内将该游客送上救援船 请说明理由.(接送游客上下船的时间忽略不计)
12.每年的11 月 9 日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB 可伸缩(最长可伸至 20 m),且可绕点 B 转动,其底部 B 离地面的距离 BC为 2m,当云梯顶端 A 在建筑物EF 所在直线上时,底部 B 到 EF 的距离 BD为9 m.
(1) 若∠ABD= 53°,求此时云梯 AB的长;
(2)如图2,若在建筑物底部 E 的正上方19 m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处 请说明理由.
(参考数据:
13.知识小提示:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足 53°≤α≤72°.(参考 数 据:sin53°≈ 0. 80, ;0.91,cos66°≈0.41,tan66°≈2.25)
如图,现有一架长4m 的梯子AB斜靠在一竖直的墙AO上.
(1)当人安全使用这架梯子时,求梯子顶端A 与地面距离的最大值;
(2)当梯子底端 B 距离墙面 1.64 m时,计算∠ABO等于多少度 并判断此时人是否能安全使用这架梯子
14.一座吊桥的钢索立柱 AD 两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得∠ABD 为 30°,由于 B、D两点间的距离不易测得,通过探究和测量,发现∠ACD 恰好为 45°,点 B与点C 之间的距离约为 16 m.已知点 B、C、D共线,AD⊥BD.求钢索 AB的长度.(结果保留根号)
15.拓展小组研制的智能操作机器人,如图 1,水平操作台为 l,底座AB 固定,高 AB 为 50cm,连杆 BC长度为70 cm,手臂CD长度为60 cm.点 B,C是转动点,且 AB,BC与CD 始终在同一平面内.
(1)转动连杆 BC,手臂 CD,使∠ABC=143°,CD∥l,如图2,求手臂端点 D 离操作台l 的高度 DE 的长(精确到 1 cm,参考数据:
(2)物品在操作台 l 上,距离底座 A 端110 cm 的点 M 处,转动连杆 BC,手臂CD,手臂端点 D 能否碰到点 M 请说明理由.
压轴预测
1.如图,Rt△ABC 中,∠BAC=90°,AD⊥BC于点D,若 AD: CD=4: 3,则 tanB的值为 ( )
A. B.
C. D.
2.某公园有一座古塔,古塔前有一个斜坡CD,坡角 ∠DCE = 42°, 斜坡高 DE =1.8米,DQ是平行于水平地面BC 的一个平台.小华想利用所学知识测量古塔的高度 AB,她在平台的点 G 处水平放置一平面镜,她沿着GQ方向移动,当移动到点 N时,刚好在镜面中看到古塔顶端点 A 的像,这时,测得小华眼睛与地面的距离MN= 1.5 米,GN=2 米,BC=16 米,DG=8米,已知 AB⊥BC,MN⊥DQ,根据题中提供的相关信息,古塔的高度 AB 约为(参考数据:sin42°≈0. 67, cos42°≈0.74,tan42°≈0.90) ( )
A.19.5米
B.19.7米
C.21.3米
D.22.1米
3.如图,C 岛在A 岛的北偏东45°方向,在 B岛的北偏西25°方向.
(1)直接写出∠ACB的度数是 ;
(2)测量发现∠BAC=20°,A 岛与C 岛之间的距离AC=20海里,求 A 岛与 B 岛之间的距离.(结果精确到0.1海里)(参考数据: 0.36)
4.某地为了让山顶通电,需要从山脚点 B 开始接驳电线,经过中转站 D,再连通到山顶点 A 处,测得山顶 A 的 高 度 AC 为300米,从山脚 B 到山顶 A 的水平距离BC 是500 米,斜面BD 的坡度i=1:2(指DF 与BF 的比),从点 D 看向点A 的仰角为 45°.
(1)斜面 AD的坡度i= ;
(2)求电线 AD+BD 的长度(结果保留根号).
参考答案
2.
4.边 角
(2)互余
(3)
5.(1)方位角
(2)水平线上方 水平线下方 ∠AOB∠AOC
(3)坡度 坡比 hl 坡角 hl
1. B 【解析】本题考查特殊角的三角函数值.tan45°=1,故选 B.
2. A 【解析】本题考查解直角三角形的实际应用.在Rt△ABC中,∠ACB=90°,所以 所以BC=12sinα米,故选 A.
3. D 【解析】本题考查解直角三角形.∵BD=2CD=6,
∴CD=3.∵tanC=2,AD 是△ABC 的高, ∴AD=6.在 Rt△ABD中,. 故选 D.
4. A 【解析】本题考查三角函数的应用、勾股定理.由题意得 则 由勾股定理得( 故选 A.
5. A 【解析】本题考查三角函数的实际应用.过点C作CF⊥AB于点 F,由题意得CF=DB=b,∵tan∠ACF=AF,∴AF=tan∠ACF×CF= btana,∴AB=AF+FB=AF+CD=a+btanα,故选 A.
【解析】本题考查解直角三角形.如图,过点C作CE⊥BD 于点 E.∵∠ABC=150°,∠BCD=105°, 1 6(
7.16 【解析】本题考查解直角三角形的实际应用.如图,过点 D作 DH⊥AB 于点 H ,易知四边形 BCDH 为矩形,则DH=BC,BH=CD=6m .由平行线的性质可知∠ADH=α=45°,∠ACB=β=58°.在 Rt△ADH 中,设AH= xm,则 DH= xm,所以 BC= xm,AB=AH+BH=(x+6)m.在 Rt△ABC 中,tan∠ACB= tan58°= 解得x≈10,则甲建筑物的高度 AB约为16 m.
8.10.4 【解析】本题考查解直角三角形的实际应用.作AD⊥BC于点 D,则∠ABC=30°,∠ACD=60°,∠BAC=30°.设CD=a,在 Rt△ACD中,AD= a,AC=BC=2a=12,
【解析】本题考查解直角三角形的应用.设上升的高度为x米,∵上山直道的坡度为1:7,∴水平距离为7x米,由勾股定理得 解得 (舍去),∴每前进 100 米所上升的高度为10 米.
10.19 cm
先在 Rt△AOC中,求出 AO的长,再在 Rt△A'OD 中,利用锐角三角函数即可求出 A'D的长.
解:由题意可知,
在 Rt△AOC中, AC=10 cm,
∴AO=2AC=20cm.
在 Rt△A'OD 中, A'O=AO=20cm,
即顶部边缘 A'处离桌面的高度A'D 的长约为 19 cm.
11.(1)1 559 米 (2)能,理由略
(1)过点 A 作AD⊥CB,交CB的延长线于点D,根据题意可得∠CAB,∠BAD的度数,再由平行线的性质及等腰三角形的判定可得AB,BD的长,进而得 CD的长,结合锐角三角函数的定义即可求出答案;(2)分别求出快艇和救援船5分钟内行驶的路程和以及实际行驶的路程和,进行比较即可得解.
解:(1)如图,过点 A 作AD⊥CB,交 CB 的延长线于点 D,则∠ADC=90°.
由题意得∠NAC=30°,∠NAB=60°.
∴∠CAB=30°,∠BAD=30°.
∵NA∥CB,
∴∠C=∠NAC=30°.
∴AB=BC=900.∴BD=450.
∴CD=900+450=1350.
∵在 Rt△ACD中.
答:湖岸 A 与码头C 的距离约为 1 559 米.
(2)在接到通知后,快艇能在5分钟内将该游客送上救援船.理由如下:
快艇和救援船5分钟一共可行驶的路程为
5×150+5×400=2750,
快艇和救援船实际行驶的路程和为
1559+900=2459.
∵2750>2459,
∴在接到通知后,快艇能在5分钟内将该游客送上救援船.
12.(1)15 m (2)能,理由略
(1)在 Rt△ABD 中,利用锐角三角函数即可求解;
(2)结合已知条件先求出AD的长,再利用勾股定理求出 AB的长,比较大小即可作出判断.
解:(1)在 Rt△ABD中,∠ABD=53°,BD=9,
答:此时云梯AB的长为15 m.
(2)∵AE=19,BC=2,
∴AD=19-2=17.
在Rt△ABD中,BD=9,
∴在该消防车不移动位置的前提下,云梯能够伸到险情处.
13.(1)3.8 米 (2)∠ABO=66°,能
(1)根据α的取值范围,确定 AO取最大值时所对应α的值,在 Rt△AOB中,由正弦的定义即可求解;(2)在Rt△AOB 中,由余弦的定义求出 cos∠ABO,再结合已知条件求出∠ABO,即可判断.
解: ,当α=72°时,AO取最大值.
在 Rt△AOB中,
∴AO=ABsin∠ABO
=4sin72°
=4×0.95
=3.8,
所以梯子顶端A 与地面的距离的最大值3.8米.
(2)在 Rt△AOB 中.
cos∠ABO=1.64÷4=0.41,cos66°≈0.41,
∴∠ABO=66°.
∴人能安全使用这架梯子.
设AD=x,根据三角函数构造关于 AD的方程,解方程进而求得AB.
解:解法一:在△ADC中,设AD=x.
∵AD⊥BD,∠ACD=45°,
∴CD=AD=x.
在△ADB中,AD⊥BD,∠ABD=30°,
∴AD=BDtan30°,
即
解之,得
∴钢索 AB 的长度约为(
解法二:在△ADB中,设AB=x.
∵AD⊥BD,∠ABD=30°,
在△ADC中,AD⊥BD,∠ACD=45°,
∴AD=CD,
即
解之,得
∴钢索 AB的长度约为(
15.(1)106 cm (2)能,理由略
(1)作CP⊥AE于点 P,BQ⊥CP 于点 Q,由 CQ+PQ计算CP 得到DE 即可;(2)根据题意画出图形,根据图形运用勾股定理求解 AD,从而即可判断.
解:(1)过点C作CP⊥AE于点 P,
过点 B作 BQ⊥CP 于点 Q,如图1,
∵∠ABC=143°,∴∠CBQ=53°,
∴在 Rt△BCQ中,
∵CD∥l,∴DE=CP=CQ+PQ=56+50=106 cm.
(2)当点 B,C,D共线时,如图2,
BD=60+70=130cm,AB=50cm,
在 Rt△ABD中,
∴AD=120 cm>110 cm.
∴手臂端点 D能碰到点 M.
压轴预测
1. C 【解析】本题考查锐角三角函数. ∵AD⊥BC,∴∠ADB=∠ADC= 90°. 又∠BAC= 90°,∴∠B +∠BAD=∠BAD+∠CAD = 90°,∴∠B=∠CAD, 故选C.
2. C 【解析】本题考查解直角三角形及相似三角形的应用.在 Rt△CDE 中, ∴CE≈2(米).延长 GD 交 AB 于点 H,则 BH=DE=1.8(米),DH=BE=BC+CE≈18(米),HG=DH+DG≈26(米).∵∠AHG=∠MNG= 90°,∠AGH=∠MGN,∴△AHG∽△MNG,∴AH:MN=HG:NG,即AH:1.5=26:2,∴AH=19.5(米),∴AB=AH+HB=21.3(米),故选 C.
中小学教育资源及组卷应用平台
3.(1)70° (2)18.8海里
(1)根据已知方位角的度数即可求解;(2)根据∠BAC的度数求出∠CBA的度数,在直角三角形中利用锐角的三角函数即可求出AB的距离.
解:(1)70°.
(2)当∠BAC=20°时,∠CBA=90°,
∴AB=AC×cos∠BAC=AC×cos20°
≈20×0.94=18.8(海里).
4.(1)1:1( 米
(1)根据斜面 AD 的坡度i=AE:DE 即可求解;(2)设AE=x,EC=y,利用斜面 BD的坡度表示出BF,在根据已知条件建立关于x和y的方程组,解方程组即可求出x和y的值,再根据勾股定理求出 BD,AD的长,相加即可求解.
解:(1)1:1.
(2)设AE=x,EC=y,
∴FC=DE=AE=x,DF=EC=y.
∵斜面 BD的坡度i=DF:BF=1:2,∴BF=2y.
依题意得 解得
根据勾股定理得
答:电线AD+BD的长度为( 米.
同课章节目录
