类型3 动态问题专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 类型3 动态问题专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 655.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 18:57:46 | ||
图片预览




文档简介
类型3 动态问题
1.运动型问题就是在三角形、矩形、梯形等一些几何图形上,设计一个或几个动点(或线或面),并对这些点(或线或面)在运动变化的过程中相伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究考查.运动型问题常常集几何、代数知识于一体,数形结合,有较强的综合性.
2.解决运动型问题需要用运动与变化的眼光去观察和研究图形,把握动点(或线或面)运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变量、不变关系和特殊关系.尽管一些试题大多属于静态的知识和方法,然而,这些试题中常常渗透着运动与变化的思想方法,需要用运动与变化的观点去研究和解决.
3.运动型问题有时把方程、不等式联系起来.当一个问题是求有关图形变量之间的关系时,通常建立函数模型或不等式模型求解;当求图形之间的特殊位置关系和一些特殊的值时,通常建立方程模型去求解.
【例 1】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点 O 为圆心,2为半径的圆与 OB 交于点C,过点 C作CD⊥OB交AB 于点D,点 P是边 OA 上的动点. 当 PC+PD 最小时,OP 的长为 ( )
A. B. C.1 D.
【解析】本题考查轴对称法确定线段和的最小值、平行线的判定和性质、平行线分线段成比例定理.如图,作点C关于直线AO的对称点,交⊙O 于点 E,连接 ED,交 AO 于点P,易知此时 PC+PD的值最小.∵CD⊥OB, ∴∠DCB= 90°. 又 ∠AOB = 90°, 解得 即 解得 故选 B.
【答案】B
【例2】如图1,△ABC中,∠ABC=60°,D 是 BC 边上的一个动点(不与点 B,C 重合),DE∥AB,交 AC 于点E,EF∥BC.交 AB 于点 F.设 BD的长为x,四边形 BDEF 的面积为y,y与x 的函数图象是如图 2 所示的一段抛物线,其顶点 P的坐标为(2,3),则AB 的长为 .
【解析】本题考查动点问题与函数图象的结合、特殊角的三角函数值.由题图 2可知,BC=4.当 BD=2时,四边形 BDEF的面积为 3,此时作 FH⊥BC于点H, ∴3 = 2 · FH,. 在Rt△BHF 中, .∵此时 D为BC 中点,且DE∥AB,∴DE为△ABC的中位线, 又 EF∥BC,∴四边形 BDEF为平行四边形,∴BF=DE= AB,∴AB=2BF=2
【答案】2
【例 3】如图,在菱形ABCD中,AB=4,∠BAD=60°,点 P 从点A 出发,沿线段 AD 以每秒 1个单位长度的速度向终点 D 运动,过点 P 作 PQ⊥AB 于点Q,作 PM⊥AD 交直线AB 于点 M,交直线 BC于点 F.设△PQM 与菱形ABCD 重叠部分图形的面积为 S(平方单位),点P 运动时间为t(秒).
(1)当点 M 与点 B 重合时,求t的值;
(2)当 t 为何值时,△APQ 与△BMF全等;
(3)求S 与t 的函数关系式;
(4)以线段 PQ 为边,在 PQ 右侧作等边三角形 PQE,当2≤t≤4 时,求点 E 运动路径的长.
【解】(1)∵菱形 ABCD 中,∠BAD=60°,
∴△ABD为等边三角形,
∴当点 P 在 AD 边中点时,PB⊥AD,点 M 与点B 重合,
∵AB=4,
∴t=2.
(2)依题意,△APQ和△BMF 都是直角三角形,
且∠PAQ=∠FBM=60°,
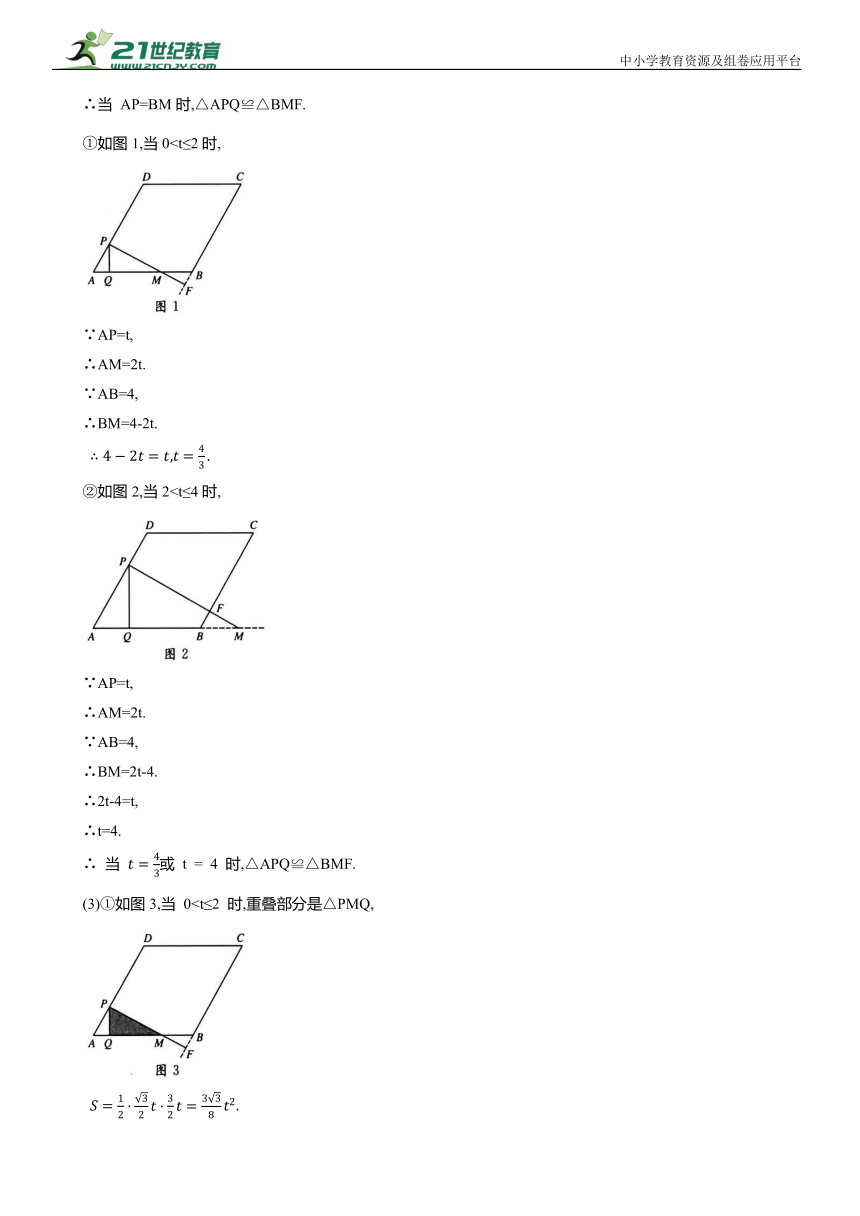
∴当 AP=BM时,△APQ≌△BMF.
①如图1,当0∵AP=t,
∴AM=2t.
∵AB=4,
∴BM=4-2t.
②如图2,当2∵AP=t,
∴AM=2t.
∵AB=4,
∴BM=2t-4.
∴2t-4=t,
∴t=4.
∴ 当 或 t = 4 时,△APQ≌△BMF.
(3)①如图3,当 0②如图4,当2S=S△PQM-S△BFM
(4) 如 图 5, ∵ 在 Rt△PQM 中,∠PMQ=30°,
∴点E 是斜边 PM 中点.
当 t=2时,点 P 在 AD 边中点 P1,此时
点E为 P1B中点 E1.
当 t=4 时,点 P 在点 D 位置,点 E 为DM1 中点 E1,同时也是 BC的中点.
∴2≤t≤4时,点E 的路径长为线段E1E2的长度.
方法一:过点 E1作 E1H⊥DE 于点 H.
在 Rt△E HE 中,
方法二:过点 E2 作 E N⊥AB 于点N,
在 Rt△E NB中,E2B=2,
在 Rt△E NA 中,AN=AB+BN=4+1=5,
由题意可得点 E1 是 AE1中点,
中小学教育资源及组卷应用平台
故
1.如图,在□ABCD 中,∠A=60°,AB =2,AD=1,点 E,F 在□ABCD的边上,从点 A 同时出发,分别沿A→B→C 和A→D→C的方向以每秒1个单位长度的速度运动,到达点 C 时停止.线段 EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x 之间函数关系的图象是 ( )
2.如图 1,在菱形 ABCD 中,∠A=60°,动点 P 从点 A 出发,沿折线AD→DC→CB方向匀速运动,运动到点 B停止.设点 P 的运动路程为x,△APB 的面积为y,y与x的函数图象如图2所示,则 AB 的长为 ( )
A.
3.如图,菱形 ABCD 中,∠B=60°,点 P 从点 B 出发,沿折线 BC-CD方向移动,移动到点 D 停止.在△ABP形状的变化过程中,依次出现的特殊三角形是 ( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
4.如图1,矩形 ABCD 中,点 E为 BC 的中点,点 P 沿 BC 从点 B 运动到点C,设 B,P 两点间的距离为x,PA-PE=y,图2是点 P 运动时y 随x 变化的关系图象,则BC的长为 ( )
A.4 B.5
C.6 D.7
5.如图,线段 AB=10,点C、D在AB 上,AC=BD=1.已知点 P从点C 出发,以每秒1个单位长度的速度沿着 AB向点 D 移动,到达点 D 后停止移动.在点 P 移动过程中作如下操作:先以点 P 为圆心,PA、PB 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 P 的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t 的函数图象大致是 ( )
6.如图 1,在△ABC 中,∠B=36°,动点 P 从点 A 出发,沿折线A→B→C 匀速运动至点 C 停止.若点 P的运动速度为 1 cm/s,设点P 的运动时间为t(s),AP 的长度为y(cm),y 与t 的函数图象 如图 2 所示,当AP 恰好平分∠BAC时t的值为 .
7.如图,在矩形 ABCD中, 动点 M从点A 出发,沿边 AD向点 D 匀速运动,动点 N 从点 B 出发,沿边BC向点C 匀速运动,连接 MN.动点 M,N 同时出发,点M 运动的速度为v ,点N运动的速度为v ,且 v8.如图,正方形 ABCD 的边长为8,点 M 在 DC 上且 DM=2,N 是 AC上的一动点,则DN + MN 的最小值是 .
9.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6 cm.动点 P 从点 A出发,以 2cm /s的速度沿边 AB 向终点 B匀速运动.以 PA为一边作∠APQ=120°,另一边 PQ 与折线AC--CB 相交于点 Q,以PQ为边作菱形 PQMN,点 N 在线段 PB上.设点 P 的运动时间为 x(s),菱形PQMN 与△ABC重叠部分图形的面积为
(1) 当点 Q 在 边 AC 上时, PQ 的长为 cm.(用含x的代数式表示)
(2)当点 M 落在边BC 上时,求x的值.
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
10.已知抛物线 c(a,c为常数,a≠0)经过点 C(0,--1),顶点为 D.
(1)当a=1时,求该抛物线的顶点坐标;
(2)当a>0时,点 E(0,1+a),若 DE=2 DC,求该抛物线的解析式;
(3)当a<--1时,点 F(0,1--a),过点 C作直线l平行于x轴,M(m,0)是x轴上的动点,N(m+3,--1)是直线 l上的动点.当a为何值时,FM+DN 的最小值为 ,并求此时点 M,N的坐标.
压轴预测
1.如图1,菱形 ABCD的一个角∠A=60°,点 F从菱形 ABCD 的顶点 A 出发,沿A→B→D以2cm/s的速度匀速运动,图2 是点 F 运动时,△FAD的面积 y(cm )随时间x(s)变化的关系图象,则AD的值为 ( )
A. B.2
C. D.5
2.如图,在边长为 4 cm的正方形 ABCD中,动点 P 沿折线 A→B→D 以 1 cm/s的速度运动到点 D,同时动点 Q 沿折线 B→D→C以 的速度运动到点 C,各自到达终点后停止运动.设运动时间为t秒,△DPQ的面积为S,则下列图象能大致反映 S与t 之间函数关系的是 ( )
3.如图,在△ABC 中,∠C=90°,AC=2,BC=6. D 是在边 BC上的动点,则 AD的最小值是 .
4.如图1,已知等腰△ABC中,AB=AC=10,BC=12,AD⊥BC,垂足为点 D,动点 P从点 A 出发,以1.5个单位/秒的速度,沿AB方向运动,同时,点Q 从点 B 出发,以1个单位/秒的速度,沿BC 方向运动,当点 P 到达点 B 时,点Q 即停止运动,设运动时间为 t秒,过点 P 作PR⊥AD,垂足为R,连接 QR,PQ,作△PQR 关于QR 的对称△MQR.
(1)如图2,当 PQ⊥AB时,求 PQ的长度;
(2)求△PBQ与△PQR 面积差的最大值;
(3)当点 M 落在△ABC 的边上时,求t的值.
5.在平面直角坐标系中,抛物线 (a≠0)经过点 A(--3,0),B(3,--3),与 y轴交于点C,连接AC,BC.
(1)求抛物线的函数表达式;
(2)如图1,点P 是线段AC 上方抛物线上的一个动点,过点 P 作PQ∥BC交AC 于点Q,当线段 PQ的长度取得最大值时,求点 P 的坐标和 PQ 长度的最大值;
(3)如图2,将抛物线 0)向右平移3个单位长度得到新抛物线,新抛物线与抛物线 交于点 D. E为新抛物线上一点,点M,N为直线 BC 上的两个动点,直接写出所有使得以点 D,E,M,N为顶点的四边形是平行四边形的点 E 的坐标,并把求其中一个点 E 的坐标的过程写出来.
类型 3 动态问题
1. A 【解析】本题考查动点问题、二次函数的图象、三角形的面积公式.由题意,当0≤x<1时, 其函数图象是抛物线的一部分,且开口向上,故排除选项 B,D;当22. B 【解析】本题考查动点问题、函数的图象、菱形的性质、等边三角形的判定与性质.连接 BD.在菱形 ABCD中,∠A=60°,∴△ABD为等边三角形.设AB=a,由题图2可知, 解得a=2 ,故选 B.
3. C 【解析】本题考查菱形的性质、等腰三角形、等边三角形的判定.当点 P 运动到 BC 中点时,AP⊥BC 于点 P,△APB为直角三角形;当点 P 与点C 重合时,△APB为等边三角形;当点 P 运动到CD 中点时,△APB 为直角三角形;当点 P 运动到与点 D 重合时,△APB为等腰三角形,故选C.
4. C 【解析】本题考查函数图象的应用、勾股定理.由图象可知当x=0时,y=1,即当点 P 在点B 处时,y=PA-PE=1,即AB-BE=1.设BE=x(x>0),则AB=x+1.又知当点 P 运动到点 E 时,y有最大值为5,此时 PE=0,∴AE=5.在 Rt△ABE中,由勾股定理得 AE = 即 解得 (舍去),∴BE=3.∵E 是BC 的中点,∴BC=2BE=6,即 BC的长为6,故选C.
5. D 【解析】本题考查探究动点问题、圆锥的侧面展开图、扇形的弧长、圆的面积公式、函数图象的应用.由题意可知,当点 P 移动时间为 t 秒时,.PA=t+1,∴PB=9-t,∴以 PA为半径的扇形的弧长 以 PB为半径的扇形的弧长 当这两个扇形围成圆锥后,底面半径分别为 .该函数图象是顶点横坐标为4的开口向上的抛物线,故选D.
【解析】本题考查动点问题、函数图象的应用、等腰三角形的性质、相似三角形的判定与性质.当AP 恰好平分∠BAC时,点 P 在BC 上运动,如图1,连接AP.由图2知AB=BC=4 cm.因为∠B=36°,AB=BC,所以∠BAC=∠C=72°.因为 AP 平分∠BAC,所以∠BAP=∠PAC=∠B=36°,所以 AP=BP,∠APC=72°=∠C,所以 AP=AC=BP.因为∠PAC=∠B,∠C=∠C,所以△APC∽△BAC,所以 所以AP =AB·PC=4(4-AP),解得 (舍负),所以. 所以当 AP 恰好平分∠BAC时,
7. 【解析】本题考查矩形的性质、勾股定理、折叠的性质、相似三角形的判定与性质、动点探究问题.设AD与A'B'相交于点Q ∴令AB=2k,BC=3k.∵四边形 ABCD是矩形,∴AD=BC=3k,DC=AB=2k,∠C=∠D=90°.在 Rt△CNB'中,由勾股定理得 即 整理得 由翻折可知,∠A'B'N=∠B=90°,∴∠DB'Q+ 又∠D=∠C=90°,∴△DB'Q∽△CNB',∴DQ: DB': ∴△DQB'∽△A'QM,∴A'Q:A'M: MQ=DQ: DB':B'Q=3:4:5.设 则 整理得 y=k, 即VIVIV 的值为-
8.10 【解析】本题考查正方形的性质、最短路径问题、勾股定理、全等三角形的判定与性质.如图,在BC 边上取BE=DM=2,连接EN,由正方形的性质可知∠ACD=∠ACB=45°,CD=BC,所以CM=CE.又CN=CN,所以△CNM≌△CNE,所以 MN=NE.连接 DE,交 AC 于点G,则当且仅当点G与点 N重合时,DN+MN取得最小值,且(
9.(1)2x (2)1 (3)当0(1)先求出∠AQP,再利用等角对等边证明△APQ是等腰三角形即可求解;(2)根据点 M 落在边 BC 上,表示出线段AP,PN,NB,再根据AB的长列出方程,即可求出x的值;(3)分0解:(1)2x.
(2)如图1,当点 M落在边 BC上时,AP=PN=NB=2x.
因为AP+PN+NB=AB=6,
所以2x+2x+2x=6.
解得x=1.
所以当点 M落在边BC 上时,x=1.
(3)如图2,当0所以
所以
如图3,当1所以
所以
如图 4,当 1.5所以
所以
评分说明:自变量取值含0或3均不扣分.
10.(1)(1,-2) 或y= (3)点M 的坐 标为 点 N 的坐标为
(1)将a的值代入抛物线的解析式,再结合点 C 的坐标,可求出抛物线的解析式,化为顶点式,即可得顶点坐标;(2)先求出抛物线的对称轴,再求出顶点坐标,过点 D作DG⊥y轴于点G,根据勾股定理表示出 DE 和DC ,结合DE和DC 的数量关系,列出关于a的方程,求出a的值,即可求出抛物线的解析式;(3)先写出点 D平移后的对应点 D'的坐标,再作点 F 关于x轴的对称点F',得出 FM+DN的最小值,再作垂线得直角三角形,利用勾股定理列出方程,求出 a 的值,即可求出点 D'和点 F'的坐标,从而求出直线 F'D'的解析式,再求出直线与x轴的交点,即可求出 m的值,最后求出点 M 和点 N 的坐标.
解:(1)当a=1时,抛物线的解析式为
∵抛物线经过点C(0,-1),
∴0-0+c=-1.
解得c=-1.
∴抛物线的解析式为
∴抛物线的顶点坐标为(1,-2).
(2)当a>0时,
由抛物线 经过点 C(0,--1),可知c=-1.
∴抛物线的解析式为
可得抛物线的对称轴为x=1.
当x=1时,y=-a-1.
∴抛物线的顶点 D 的坐标为(1,-a-1).
过点 D作DG⊥y轴于点G.
在 Rt△DEG中,DG=1,
EG=1+a-(-a-1)=2a+2,
在Rt△DCG中,DG=1,CG=-1-(-a-1)=a,
即
解得
∴抛物线的解析式为 或 3x-1.
(3)当a<-1时,将点 D(1,-a-1)向左平移3个单位长度,向上平移1个单位长度得点 D′(-2,-a).
作点 F 关 于 x 轴 的 对 称点 F′, 得 点 F′的 坐标为(0,a-1).
当满足条件的点 M 落在线段 F'D'上时,FM+DN 最小,此时,
过点 D'作D'H⊥y轴于点 H.
在Rt△F'D'H 中,
F'H=-a-(a-1)=1-2a,
又
即(
解得 (舍).
∴点 F'的坐标为
点 D'的坐标为
可得直线 F'D'的解析式为
当y=0时,
∴点 M 的 坐 标 为 点 N 的 坐 标 为
压轴预测
1. B 【解析】本题考查菱形的性质、函数图象的实际应用.根据题意可得当点 F 运动到点 B 时,△FAD 的面积y取得最大值 ,即 如图,过点 B 作 BE⊥AD,垂足为点 E,因为∠A=60°,四边形 ABCD为菱形,所以 则 解得AD=2,故选 B.
2. D 【解析】本题考查动点问题、函数的图象.由题意得当0【解析】本题考查直角三角形的性质、锐角三角函数,勾股定理.如图,过D 点在三角形外部构造Rt△BDE,DE⊥BE,∠DBE=α,使得 则cosα= 在Rt△ABC中,AC=2,BC=6,则 令∠ABC=β,则 D为BC上一动点,求 的最小值就是求 DE+AD的最小值,由“两点之间,线段最短”,可知当 D,A,E三点共线时,DE+AD有最小值,此时过A 点作AF⊥BE,垂足为 F,交 BC于点D',此时 AF 即为最小值.在Rt△ABF 中,sin∠ABE= sin(α+β)= sinαcosβ+cosαsinβ= 求得/ 即 的最小值为
4.(1) (2) 或 或6 或 或
(1)根据已知用 t 表示出线段BP,BQ,再根据锐角三角函数列出方程,求出 t的值,即可求出 PQ 的长;(2)过点 P 作PE⊥BC于点E,根据相似三角形的性质表示出PE,再表示出 PR,代入三角形的面积公式,可整理得二次函数,即可求出两个三角形的面积差的最大值;(3)分情况讨论:当点 M落在BC 上时,判定四边形 PRMQ是菱形,根据菱形的性质表示出线段的长,利用勾股定理列出方程,求出 t 的值;当点 M 落在AC 上时,点Q 与点D 重合,DR 与AD 重合,此时t=BD=6;当点 Q与点D 不重合时,延长 PR交AC 于点 T,由对称得线段相等,利用三角形的内角和定理证明 PM⊥AC,根据平行线的性质,利用锐角三角函数列出方程,求出 t的值;当点 M落在AB 上时,延长QR 交AB 于N,根据垂直得直角三角形,利用锐角三角函数表示出线段的长,再根据勾股定理列出方程,求出 t 的值.
解:(1)∵AB=AC=10,AD⊥BC,BC=12,∴BD=CD=6.
由勾股定理得AD=8,
由点的运动可知,BP=10-1.5t,BQ=t,
当 PQ⊥AB时,
解得
(2)如图,过点 P 作PE⊥BC 于点E,
则PE∥AD,∴△BPE∽△BAD,
即
抛物线开口向下,
∴当 时, 的最大值为
(3)①当点 Q与点D 不重合时,点 M 落在BC 上,如图,设 PM,RQ交于点O,
∵△PQR 和△MQR 关于 QR 对称,
∴PQ=MQ,PR=MR,PM⊥QR,
∴∠RPM=∠RMP.
∵PR∥QM,∴∠RPM=∠PMQ,
∴∠RMP=∠PMQ.
又∠ROM=∠QOM,OM=OM,
∴△ROM≌△QOM,∴RM=QM,
∴RM=QM=QP=PR,
∴四边形 PRMQ是菱形,
∴QM=PR=0.9t.
∵RD=AD-AR=8-1.2t,
DM=QM-QD=0.9t-(6-t)=1.9t-6,RM=QM=0.9t.
在 Rt△RDM中,由勾股定理可得
解得 或
②当点 M落在AC 上时,点 Q 与点 D 重合,DR 与AD重合,此时t=BD=6;
当点 Q与点D 不重合时,延长 PR 交AC 于点T,由对称可知 PR=MR=RT=0.9t,RQ⊥PM,
∴PM⊥AC,
∴PQ∥AC,
∴∠RQD=∠C,
解得
③当点 M落在AB 上时,如图,延长QR 交AB 于N,则 QN⊥AB,
在 Rt△RDQ中,
由勾股定理可得
解得
综上所述,当点 M 落在△ABC 的边上时,t的值为 或 或6或
5.(1)y=- x - x+3 ( 或
(1)将点 A,B代入函数关系式,求出a,b的值,即可求出抛物线的解析式;(2)求出抛物线与 y轴的交点C 的坐标,求出直线 AC 的解析式,过点 P 作 PH⊥x轴,交 AC于点H,过点 B作BI∥AC,交 y轴于点I,可求出直线 BI的解析式,由平行线得三角形相似,根据比例式用含 PH 的代数式表示 PQ,根据函数关系式设点 P,H的坐标,表示出线段 PH,配方后求出最大值,即可求出PQ的最大值,并求出此时点 P 的坐标;(3)将抛物线平移后求出解析式,求出点 D 的坐标.分两种情况讨论:①当 DE为平行四边形的边时;②当 DE为平行四边形的对角线时.
解:(1)∵抛物线 经过点 A(-3,0),B(3,-3),
解得
∴抛物线的函数表达式为
(2)∵抛物线 与y轴交于点C,∴C(0,3),
∴直线 AC
过点 P 作PH⊥x轴,交 AC于点 H,
过点 B作BI∥AC交y轴于点I,
∴直线 BI:y=x-6,即I(0,-6),∴CI=9.
∵PQ∥BC,∴△PQH∽△CBI,
∴当 PH取得最大值时,PQ也取得最大值.
设
且--3∴当 时,PH 取得最大值,
此时点P的坐标为(
(3) 点 E 的 坐 标 为 (8, 一 12),
将抛物线 向右平移3个单位长度后,所得新抛物线为
∴点 D 的坐标为(1,2).
①当 DE为平行四边形的边时,
此时DE∥MN,过点 D 作直线BC 的平行线,与抛物线为 的交点即为所求点E,
∵直线BC:y=-2x+3,
∴直线DE:y=-2x+4.
联立 解得 (舍)
∴点 E 的坐标为(8,-12).
②当DE为平行四边形的对角线时,此时,对角线的中点Q在直线BC 上.
设
则
∵直线BC:y=-2x+3,
解得
即点 E 的坐标为
或
综上,点E的坐标为
或
1.运动型问题就是在三角形、矩形、梯形等一些几何图形上,设计一个或几个动点(或线或面),并对这些点(或线或面)在运动变化的过程中相伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究考查.运动型问题常常集几何、代数知识于一体,数形结合,有较强的综合性.
2.解决运动型问题需要用运动与变化的眼光去观察和研究图形,把握动点(或线或面)运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变量、不变关系和特殊关系.尽管一些试题大多属于静态的知识和方法,然而,这些试题中常常渗透着运动与变化的思想方法,需要用运动与变化的观点去研究和解决.
3.运动型问题有时把方程、不等式联系起来.当一个问题是求有关图形变量之间的关系时,通常建立函数模型或不等式模型求解;当求图形之间的特殊位置关系和一些特殊的值时,通常建立方程模型去求解.
【例 1】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点 O 为圆心,2为半径的圆与 OB 交于点C,过点 C作CD⊥OB交AB 于点D,点 P是边 OA 上的动点. 当 PC+PD 最小时,OP 的长为 ( )
A. B. C.1 D.
【解析】本题考查轴对称法确定线段和的最小值、平行线的判定和性质、平行线分线段成比例定理.如图,作点C关于直线AO的对称点,交⊙O 于点 E,连接 ED,交 AO 于点P,易知此时 PC+PD的值最小.∵CD⊥OB, ∴∠DCB= 90°. 又 ∠AOB = 90°, 解得 即 解得 故选 B.
【答案】B
【例2】如图1,△ABC中,∠ABC=60°,D 是 BC 边上的一个动点(不与点 B,C 重合),DE∥AB,交 AC 于点E,EF∥BC.交 AB 于点 F.设 BD的长为x,四边形 BDEF 的面积为y,y与x 的函数图象是如图 2 所示的一段抛物线,其顶点 P的坐标为(2,3),则AB 的长为 .
【解析】本题考查动点问题与函数图象的结合、特殊角的三角函数值.由题图 2可知,BC=4.当 BD=2时,四边形 BDEF的面积为 3,此时作 FH⊥BC于点H, ∴3 = 2 · FH,. 在Rt△BHF 中, .∵此时 D为BC 中点,且DE∥AB,∴DE为△ABC的中位线, 又 EF∥BC,∴四边形 BDEF为平行四边形,∴BF=DE= AB,∴AB=2BF=2
【答案】2
【例 3】如图,在菱形ABCD中,AB=4,∠BAD=60°,点 P 从点A 出发,沿线段 AD 以每秒 1个单位长度的速度向终点 D 运动,过点 P 作 PQ⊥AB 于点Q,作 PM⊥AD 交直线AB 于点 M,交直线 BC于点 F.设△PQM 与菱形ABCD 重叠部分图形的面积为 S(平方单位),点P 运动时间为t(秒).
(1)当点 M 与点 B 重合时,求t的值;
(2)当 t 为何值时,△APQ 与△BMF全等;
(3)求S 与t 的函数关系式;
(4)以线段 PQ 为边,在 PQ 右侧作等边三角形 PQE,当2≤t≤4 时,求点 E 运动路径的长.
【解】(1)∵菱形 ABCD 中,∠BAD=60°,
∴△ABD为等边三角形,
∴当点 P 在 AD 边中点时,PB⊥AD,点 M 与点B 重合,
∵AB=4,
∴t=2.
(2)依题意,△APQ和△BMF 都是直角三角形,
且∠PAQ=∠FBM=60°,
∴当 AP=BM时,△APQ≌△BMF.
①如图1,当0
∴AM=2t.
∵AB=4,
∴BM=4-2t.
②如图2,当2
∴AM=2t.
∵AB=4,
∴BM=2t-4.
∴2t-4=t,
∴t=4.
∴ 当 或 t = 4 时,△APQ≌△BMF.
(3)①如图3,当 0
(4) 如 图 5, ∵ 在 Rt△PQM 中,∠PMQ=30°,
∴点E 是斜边 PM 中点.
当 t=2时,点 P 在 AD 边中点 P1,此时
点E为 P1B中点 E1.
当 t=4 时,点 P 在点 D 位置,点 E 为DM1 中点 E1,同时也是 BC的中点.
∴2≤t≤4时,点E 的路径长为线段E1E2的长度.
方法一:过点 E1作 E1H⊥DE 于点 H.
在 Rt△E HE 中,
方法二:过点 E2 作 E N⊥AB 于点N,
在 Rt△E NB中,E2B=2,
在 Rt△E NA 中,AN=AB+BN=4+1=5,
由题意可得点 E1 是 AE1中点,
中小学教育资源及组卷应用平台
故
1.如图,在□ABCD 中,∠A=60°,AB =2,AD=1,点 E,F 在□ABCD的边上,从点 A 同时出发,分别沿A→B→C 和A→D→C的方向以每秒1个单位长度的速度运动,到达点 C 时停止.线段 EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x 之间函数关系的图象是 ( )
2.如图 1,在菱形 ABCD 中,∠A=60°,动点 P 从点 A 出发,沿折线AD→DC→CB方向匀速运动,运动到点 B停止.设点 P 的运动路程为x,△APB 的面积为y,y与x的函数图象如图2所示,则 AB 的长为 ( )
A.
3.如图,菱形 ABCD 中,∠B=60°,点 P 从点 B 出发,沿折线 BC-CD方向移动,移动到点 D 停止.在△ABP形状的变化过程中,依次出现的特殊三角形是 ( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
4.如图1,矩形 ABCD 中,点 E为 BC 的中点,点 P 沿 BC 从点 B 运动到点C,设 B,P 两点间的距离为x,PA-PE=y,图2是点 P 运动时y 随x 变化的关系图象,则BC的长为 ( )
A.4 B.5
C.6 D.7
5.如图,线段 AB=10,点C、D在AB 上,AC=BD=1.已知点 P从点C 出发,以每秒1个单位长度的速度沿着 AB向点 D 移动,到达点 D 后停止移动.在点 P 移动过程中作如下操作:先以点 P 为圆心,PA、PB 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 P 的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t 的函数图象大致是 ( )
6.如图 1,在△ABC 中,∠B=36°,动点 P 从点 A 出发,沿折线A→B→C 匀速运动至点 C 停止.若点 P的运动速度为 1 cm/s,设点P 的运动时间为t(s),AP 的长度为y(cm),y 与t 的函数图象 如图 2 所示,当AP 恰好平分∠BAC时t的值为 .
7.如图,在矩形 ABCD中, 动点 M从点A 出发,沿边 AD向点 D 匀速运动,动点 N 从点 B 出发,沿边BC向点C 匀速运动,连接 MN.动点 M,N 同时出发,点M 运动的速度为v ,点N运动的速度为v ,且 v
9.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6 cm.动点 P 从点 A出发,以 2cm /s的速度沿边 AB 向终点 B匀速运动.以 PA为一边作∠APQ=120°,另一边 PQ 与折线AC--CB 相交于点 Q,以PQ为边作菱形 PQMN,点 N 在线段 PB上.设点 P 的运动时间为 x(s),菱形PQMN 与△ABC重叠部分图形的面积为
(1) 当点 Q 在 边 AC 上时, PQ 的长为 cm.(用含x的代数式表示)
(2)当点 M 落在边BC 上时,求x的值.
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
10.已知抛物线 c(a,c为常数,a≠0)经过点 C(0,--1),顶点为 D.
(1)当a=1时,求该抛物线的顶点坐标;
(2)当a>0时,点 E(0,1+a),若 DE=2 DC,求该抛物线的解析式;
(3)当a<--1时,点 F(0,1--a),过点 C作直线l平行于x轴,M(m,0)是x轴上的动点,N(m+3,--1)是直线 l上的动点.当a为何值时,FM+DN 的最小值为 ,并求此时点 M,N的坐标.
压轴预测
1.如图1,菱形 ABCD的一个角∠A=60°,点 F从菱形 ABCD 的顶点 A 出发,沿A→B→D以2cm/s的速度匀速运动,图2 是点 F 运动时,△FAD的面积 y(cm )随时间x(s)变化的关系图象,则AD的值为 ( )
A. B.2
C. D.5
2.如图,在边长为 4 cm的正方形 ABCD中,动点 P 沿折线 A→B→D 以 1 cm/s的速度运动到点 D,同时动点 Q 沿折线 B→D→C以 的速度运动到点 C,各自到达终点后停止运动.设运动时间为t秒,△DPQ的面积为S,则下列图象能大致反映 S与t 之间函数关系的是 ( )
3.如图,在△ABC 中,∠C=90°,AC=2,BC=6. D 是在边 BC上的动点,则 AD的最小值是 .
4.如图1,已知等腰△ABC中,AB=AC=10,BC=12,AD⊥BC,垂足为点 D,动点 P从点 A 出发,以1.5个单位/秒的速度,沿AB方向运动,同时,点Q 从点 B 出发,以1个单位/秒的速度,沿BC 方向运动,当点 P 到达点 B 时,点Q 即停止运动,设运动时间为 t秒,过点 P 作PR⊥AD,垂足为R,连接 QR,PQ,作△PQR 关于QR 的对称△MQR.
(1)如图2,当 PQ⊥AB时,求 PQ的长度;
(2)求△PBQ与△PQR 面积差的最大值;
(3)当点 M 落在△ABC 的边上时,求t的值.
5.在平面直角坐标系中,抛物线 (a≠0)经过点 A(--3,0),B(3,--3),与 y轴交于点C,连接AC,BC.
(1)求抛物线的函数表达式;
(2)如图1,点P 是线段AC 上方抛物线上的一个动点,过点 P 作PQ∥BC交AC 于点Q,当线段 PQ的长度取得最大值时,求点 P 的坐标和 PQ 长度的最大值;
(3)如图2,将抛物线 0)向右平移3个单位长度得到新抛物线,新抛物线与抛物线 交于点 D. E为新抛物线上一点,点M,N为直线 BC 上的两个动点,直接写出所有使得以点 D,E,M,N为顶点的四边形是平行四边形的点 E 的坐标,并把求其中一个点 E 的坐标的过程写出来.
类型 3 动态问题
1. A 【解析】本题考查动点问题、二次函数的图象、三角形的面积公式.由题意,当0≤x<1时, 其函数图象是抛物线的一部分,且开口向上,故排除选项 B,D;当2
3. C 【解析】本题考查菱形的性质、等腰三角形、等边三角形的判定.当点 P 运动到 BC 中点时,AP⊥BC 于点 P,△APB为直角三角形;当点 P 与点C 重合时,△APB为等边三角形;当点 P 运动到CD 中点时,△APB 为直角三角形;当点 P 运动到与点 D 重合时,△APB为等腰三角形,故选C.
4. C 【解析】本题考查函数图象的应用、勾股定理.由图象可知当x=0时,y=1,即当点 P 在点B 处时,y=PA-PE=1,即AB-BE=1.设BE=x(x>0),则AB=x+1.又知当点 P 运动到点 E 时,y有最大值为5,此时 PE=0,∴AE=5.在 Rt△ABE中,由勾股定理得 AE = 即 解得 (舍去),∴BE=3.∵E 是BC 的中点,∴BC=2BE=6,即 BC的长为6,故选C.
5. D 【解析】本题考查探究动点问题、圆锥的侧面展开图、扇形的弧长、圆的面积公式、函数图象的应用.由题意可知,当点 P 移动时间为 t 秒时,.PA=t+1,∴PB=9-t,∴以 PA为半径的扇形的弧长 以 PB为半径的扇形的弧长 当这两个扇形围成圆锥后,底面半径分别为 .该函数图象是顶点横坐标为4的开口向上的抛物线,故选D.
【解析】本题考查动点问题、函数图象的应用、等腰三角形的性质、相似三角形的判定与性质.当AP 恰好平分∠BAC时,点 P 在BC 上运动,如图1,连接AP.由图2知AB=BC=4 cm.因为∠B=36°,AB=BC,所以∠BAC=∠C=72°.因为 AP 平分∠BAC,所以∠BAP=∠PAC=∠B=36°,所以 AP=BP,∠APC=72°=∠C,所以 AP=AC=BP.因为∠PAC=∠B,∠C=∠C,所以△APC∽△BAC,所以 所以AP =AB·PC=4(4-AP),解得 (舍负),所以. 所以当 AP 恰好平分∠BAC时,
7. 【解析】本题考查矩形的性质、勾股定理、折叠的性质、相似三角形的判定与性质、动点探究问题.设AD与A'B'相交于点Q ∴令AB=2k,BC=3k.∵四边形 ABCD是矩形,∴AD=BC=3k,DC=AB=2k,∠C=∠D=90°.在 Rt△CNB'中,由勾股定理得 即 整理得 由翻折可知,∠A'B'N=∠B=90°,∴∠DB'Q+ 又∠D=∠C=90°,∴△DB'Q∽△CNB',∴DQ: DB': ∴△DQB'∽△A'QM,∴A'Q:A'M: MQ=DQ: DB':B'Q=3:4:5.设 则 整理得 y=k, 即VIVIV 的值为-
8.10 【解析】本题考查正方形的性质、最短路径问题、勾股定理、全等三角形的判定与性质.如图,在BC 边上取BE=DM=2,连接EN,由正方形的性质可知∠ACD=∠ACB=45°,CD=BC,所以CM=CE.又CN=CN,所以△CNM≌△CNE,所以 MN=NE.连接 DE,交 AC 于点G,则当且仅当点G与点 N重合时,DN+MN取得最小值,且(
9.(1)2x (2)1 (3)当0
(2)如图1,当点 M落在边 BC上时,AP=PN=NB=2x.
因为AP+PN+NB=AB=6,
所以2x+2x+2x=6.
解得x=1.
所以当点 M落在边BC 上时,x=1.
(3)如图2,当0
所以
如图3,当1
所以
如图 4,当 1.5
所以
评分说明:自变量取值含0或3均不扣分.
10.(1)(1,-2) 或y= (3)点M 的坐 标为 点 N 的坐标为
(1)将a的值代入抛物线的解析式,再结合点 C 的坐标,可求出抛物线的解析式,化为顶点式,即可得顶点坐标;(2)先求出抛物线的对称轴,再求出顶点坐标,过点 D作DG⊥y轴于点G,根据勾股定理表示出 DE 和DC ,结合DE和DC 的数量关系,列出关于a的方程,求出a的值,即可求出抛物线的解析式;(3)先写出点 D平移后的对应点 D'的坐标,再作点 F 关于x轴的对称点F',得出 FM+DN的最小值,再作垂线得直角三角形,利用勾股定理列出方程,求出 a 的值,即可求出点 D'和点 F'的坐标,从而求出直线 F'D'的解析式,再求出直线与x轴的交点,即可求出 m的值,最后求出点 M 和点 N 的坐标.
解:(1)当a=1时,抛物线的解析式为
∵抛物线经过点C(0,-1),
∴0-0+c=-1.
解得c=-1.
∴抛物线的解析式为
∴抛物线的顶点坐标为(1,-2).
(2)当a>0时,
由抛物线 经过点 C(0,--1),可知c=-1.
∴抛物线的解析式为
可得抛物线的对称轴为x=1.
当x=1时,y=-a-1.
∴抛物线的顶点 D 的坐标为(1,-a-1).
过点 D作DG⊥y轴于点G.
在 Rt△DEG中,DG=1,
EG=1+a-(-a-1)=2a+2,
在Rt△DCG中,DG=1,CG=-1-(-a-1)=a,
即
解得
∴抛物线的解析式为 或 3x-1.
(3)当a<-1时,将点 D(1,-a-1)向左平移3个单位长度,向上平移1个单位长度得点 D′(-2,-a).
作点 F 关 于 x 轴 的 对 称点 F′, 得 点 F′的 坐标为(0,a-1).
当满足条件的点 M 落在线段 F'D'上时,FM+DN 最小,此时,
过点 D'作D'H⊥y轴于点 H.
在Rt△F'D'H 中,
F'H=-a-(a-1)=1-2a,
又
即(
解得 (舍).
∴点 F'的坐标为
点 D'的坐标为
可得直线 F'D'的解析式为
当y=0时,
∴点 M 的 坐 标 为 点 N 的 坐 标 为
压轴预测
1. B 【解析】本题考查菱形的性质、函数图象的实际应用.根据题意可得当点 F 运动到点 B 时,△FAD 的面积y取得最大值 ,即 如图,过点 B 作 BE⊥AD,垂足为点 E,因为∠A=60°,四边形 ABCD为菱形,所以 则 解得AD=2,故选 B.
2. D 【解析】本题考查动点问题、函数的图象.由题意得当0
4.(1) (2) 或 或6 或 或
(1)根据已知用 t 表示出线段BP,BQ,再根据锐角三角函数列出方程,求出 t的值,即可求出 PQ 的长;(2)过点 P 作PE⊥BC于点E,根据相似三角形的性质表示出PE,再表示出 PR,代入三角形的面积公式,可整理得二次函数,即可求出两个三角形的面积差的最大值;(3)分情况讨论:当点 M落在BC 上时,判定四边形 PRMQ是菱形,根据菱形的性质表示出线段的长,利用勾股定理列出方程,求出 t 的值;当点 M 落在AC 上时,点Q 与点D 重合,DR 与AD 重合,此时t=BD=6;当点 Q与点D 不重合时,延长 PR交AC 于点 T,由对称得线段相等,利用三角形的内角和定理证明 PM⊥AC,根据平行线的性质,利用锐角三角函数列出方程,求出 t的值;当点 M落在AB 上时,延长QR 交AB 于N,根据垂直得直角三角形,利用锐角三角函数表示出线段的长,再根据勾股定理列出方程,求出 t 的值.
解:(1)∵AB=AC=10,AD⊥BC,BC=12,∴BD=CD=6.
由勾股定理得AD=8,
由点的运动可知,BP=10-1.5t,BQ=t,
当 PQ⊥AB时,
解得
(2)如图,过点 P 作PE⊥BC 于点E,
则PE∥AD,∴△BPE∽△BAD,
即
抛物线开口向下,
∴当 时, 的最大值为
(3)①当点 Q与点D 不重合时,点 M 落在BC 上,如图,设 PM,RQ交于点O,
∵△PQR 和△MQR 关于 QR 对称,
∴PQ=MQ,PR=MR,PM⊥QR,
∴∠RPM=∠RMP.
∵PR∥QM,∴∠RPM=∠PMQ,
∴∠RMP=∠PMQ.
又∠ROM=∠QOM,OM=OM,
∴△ROM≌△QOM,∴RM=QM,
∴RM=QM=QP=PR,
∴四边形 PRMQ是菱形,
∴QM=PR=0.9t.
∵RD=AD-AR=8-1.2t,
DM=QM-QD=0.9t-(6-t)=1.9t-6,RM=QM=0.9t.
在 Rt△RDM中,由勾股定理可得
解得 或
②当点 M落在AC 上时,点 Q 与点 D 重合,DR 与AD重合,此时t=BD=6;
当点 Q与点D 不重合时,延长 PR 交AC 于点T,由对称可知 PR=MR=RT=0.9t,RQ⊥PM,
∴PM⊥AC,
∴PQ∥AC,
∴∠RQD=∠C,
解得
③当点 M落在AB 上时,如图,延长QR 交AB 于N,则 QN⊥AB,
在 Rt△RDQ中,
由勾股定理可得
解得
综上所述,当点 M 落在△ABC 的边上时,t的值为 或 或6或
5.(1)y=- x - x+3 ( 或
(1)将点 A,B代入函数关系式,求出a,b的值,即可求出抛物线的解析式;(2)求出抛物线与 y轴的交点C 的坐标,求出直线 AC 的解析式,过点 P 作 PH⊥x轴,交 AC于点H,过点 B作BI∥AC,交 y轴于点I,可求出直线 BI的解析式,由平行线得三角形相似,根据比例式用含 PH 的代数式表示 PQ,根据函数关系式设点 P,H的坐标,表示出线段 PH,配方后求出最大值,即可求出PQ的最大值,并求出此时点 P 的坐标;(3)将抛物线平移后求出解析式,求出点 D 的坐标.分两种情况讨论:①当 DE为平行四边形的边时;②当 DE为平行四边形的对角线时.
解:(1)∵抛物线 经过点 A(-3,0),B(3,-3),
解得
∴抛物线的函数表达式为
(2)∵抛物线 与y轴交于点C,∴C(0,3),
∴直线 AC
过点 P 作PH⊥x轴,交 AC于点 H,
过点 B作BI∥AC交y轴于点I,
∴直线 BI:y=x-6,即I(0,-6),∴CI=9.
∵PQ∥BC,∴△PQH∽△CBI,
∴当 PH取得最大值时,PQ也取得最大值.
设
且--3
此时点P的坐标为(
(3) 点 E 的 坐 标 为 (8, 一 12),
将抛物线 向右平移3个单位长度后,所得新抛物线为
∴点 D 的坐标为(1,2).
①当 DE为平行四边形的边时,
此时DE∥MN,过点 D 作直线BC 的平行线,与抛物线为 的交点即为所求点E,
∵直线BC:y=-2x+3,
∴直线DE:y=-2x+4.
联立 解得 (舍)
∴点 E 的坐标为(8,-12).
②当DE为平行四边形的对角线时,此时,对角线的中点Q在直线BC 上.
设
则
∵直线BC:y=-2x+3,
解得
即点 E 的坐标为
或
综上,点E的坐标为
或
同课章节目录
