类型9 探究性问题 专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 类型9 探究性问题 专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 700.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
类型9 探究性问题
压轴例题精讲
【例】有公共顶点 A 的正方形ABCD 与正方形AEGF 按如图1 所示放置,点 E,F 分别在边 AB 和AD 上,连接 BF,DE,M 是 BF 的中点,连接 AM 交DE 于点 N.
(1)线段 DE 与 AM 之间的数量关系是 ,位置关系是 ;
(2)将图1中的正方形AEGF 绕点 A 顺时针旋转 45°,点 G 恰好落在边 AB 上,如图2,其他条件不变,线段 DE 与AM 之间的关系是否仍然成立 并说明理由.
【解】(1)DE=2AM DE⊥AM.
(2)仍然成立.理由如下:
如图,延长 AM 到点 H,使 MH=AM,连接BH.
∵点 M是BF 的中点,∴BM=FM.
又∠BMH=∠AMF,
∴△BHM≌△FAM,
∴BH=AF=AE,∠H=∠FAM,
∴AF∥BH,
∴∠FAB+∠ABH=180°.
又∵ ∠EAF + ∠BAD = ∠DAE +∠BAF=180°,
∴∠ABH=∠DAE.又AB=AD,
∴△ABH≌△DAE,∴AH=DE.
∵AH=2AM,∴DE=2AM.
又 ∠BAH = ∠ADE, ∠BAH +∠DAN=90°,
∴∠ADE+∠DAN=90°,
∴∠AND=90°,
中小学教育资源及组卷应用平台
即 DE⊥AM.
1.问题提出 如图1,在△ABC中,AB=AC,D是AC 的中点,延长 BC至点 E,使 DE = DB,延长 ED 交 AB 于点F,探究 的值.
问题探究 (1)先将问题特殊化.如图2,当∠BAC=60°时,直接写出 的值;
(2)再探究一般情形.如图1,证明(1)中的结论仍然成立.
问题拓展 如图3,在△ABC 中,AB=AC,D 是AC 的中点,G是边BC 上一点, 延长 BC至点E,使 DE=DG,延长 ED交AB 于点 F.直接写出 的值(用含 n的式子表示).
2.如图,二次函数 的图象与x轴交于A,B 两点(点 A 在点 B 的左侧),与y轴交于点 C.点P 是第一象限内二次函数图象上的一个动点,设点 P 的横坐标为m.过点 P 作直线 PD⊥x轴于点D,作直线 BC交 PD 于点 E.
(1)求A,B,C三点的坐标,并直接写出直线 BC的函数表达式;
(2)当△CEP 是以 PE 为底边的等腰三角形时,求点 P 的坐标;
(3)连接 AC,过点 P 作直线l∥ AC,交y轴于点 F,连接 DF.试探究:在点 P 运动的过程中,是否存在点 P,使得CE=FD,若存在,请直接写出 m的值;若不存在,请说明理由.
3.综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片 ABCD,使 AD 与BC 重合,得到折痕 EF,把纸片展平;
操作二:在 AD 上选一点 P,沿 BP 折叠,使点 A 落在矩形内部点 M 处,把纸片展平,连接 PM,BM.
根据以上操作,当点 M 在 EF 上时,写出图1中一个30°的角: ;
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长 PM交CD 于点Q,连接 BQ.
①如图2,当点 M 在 EF 上时,∠MBQ= °,∠CBQ= °;
②改变点 P 在 AD 上的位置(点 P 不与点A,D 重合),如图 3,判断∠MBQ 与∠CBQ的数量关系,并说明理由;
(3)拓展应用
在(2)的探究中,已知正方形纸片 ABCD的边长为8cm,当FQ=1 cm时,直接写出AP 的长.
4.在△ABC中,∠ACB= D是边BC上一点,将△ABD沿AD 折叠得到△AED,连接 BE.
(1)特例发现 如图1,当m=1,AE落在直线AC上时,
①求证:∠DAC=∠EBC;
②填空: 的值为 ;
(2)类比探究 如图2,当 m≠1,AE与边BC 相交时,
在 AD 上取一点G,使∠ACG=∠BCE,CG交 AE 于点 H.探究( 的值(用含m的式子表示),并写出探究过程;
(3)拓展运用 在(2)的条件下,当 D是BC 的中点时,若EB·EH=6,求 CG的长.
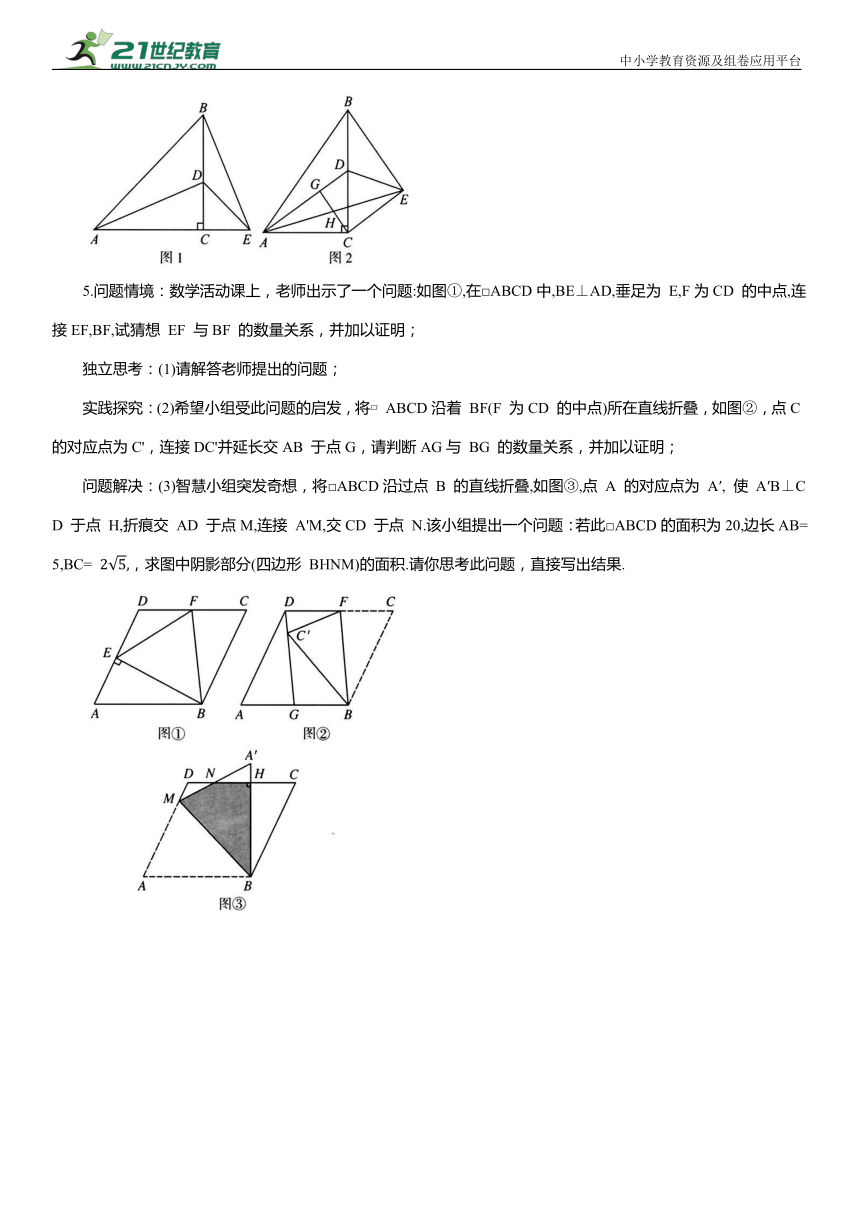
5.问题情境:数学活动课上,老师出示了一个问题:如图①,在□ABCD中,BE⊥AD,垂足为 E,F为CD 的中点,连接EF,BF,试猜想 EF 与BF 的数量关系,并加以证明;
独立思考:(1)请解答老师提出的问题;
实践探究:(2)希望小组受此问题的启发,将 ABCD沿着 BF(F 为CD 的中点)所在直线折叠,如图②,点C 的对应点为C',连接DC'并延长交AB 于点G,请判断AG与 BG 的数量关系,并加以证明;
问题解决:(3)智慧小组突发奇想,将□ABCD沿过点 B 的直线折叠,如图③,点 A 的对应点为 A′, 使 A′B⊥CD 于点 H,折痕交 AD 于点M,连接 A'M,交CD 于点 N.该小组提出一个问题:若此□ABCD的面积为20,边长AB=5,BC= ,求图中阴影部分(四边形 BHNM)的面积.请你思考此问题,直接写出结果.
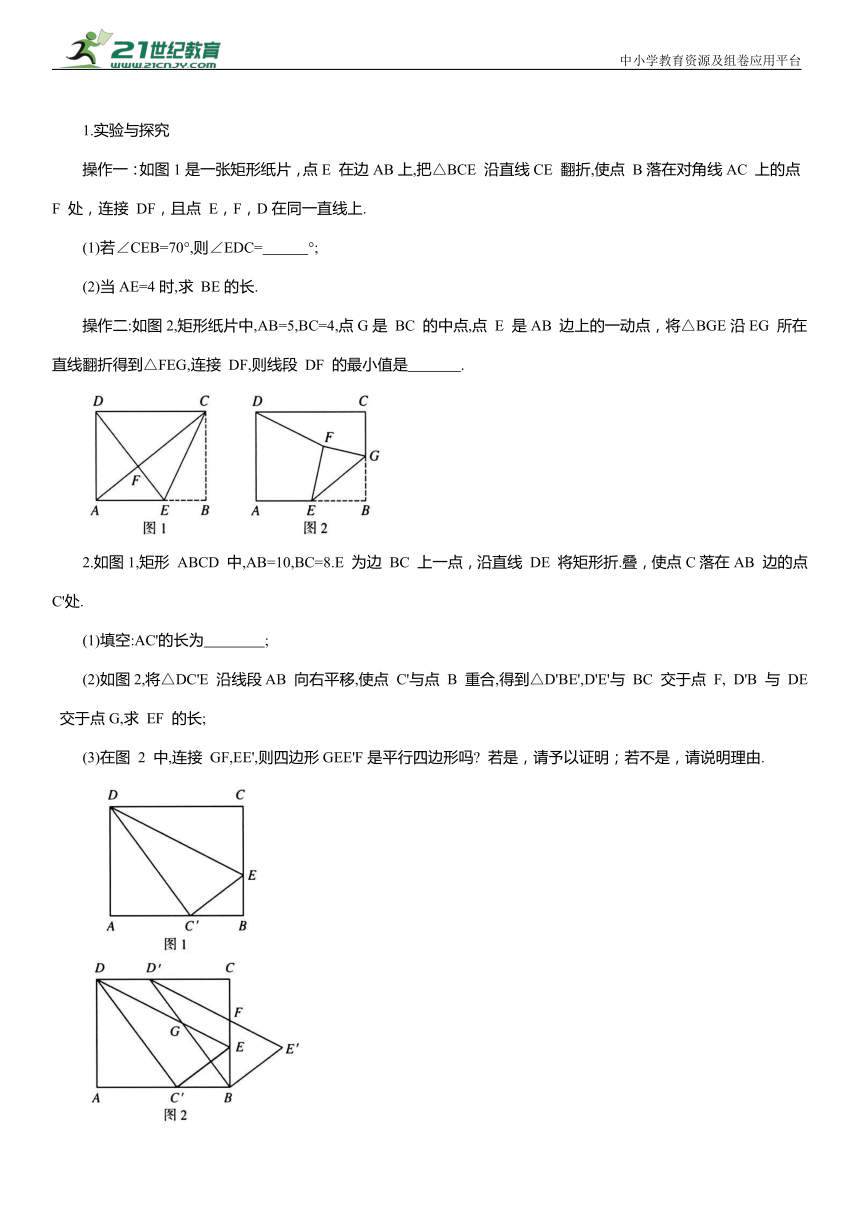
1.实验与探究
操作一:如图1是一张矩形纸片,点E 在边AB上,把△BCE 沿直线CE 翻折,使点 B落在对角线AC 上的点 F 处,连接 DF,且点 E,F,D在同一直线上.
(1)若∠CEB=70°,则∠EDC= °;
(2)当AE=4时,求 BE的长.
操作二:如图2,矩形纸片中,AB=5,BC=4,点G是 BC 的中点,点 E 是AB 边上的一动点,将△BGE沿EG 所在直线翻折得到△FEG,连接 DF,则线段 DF 的最小值是 .
2.如图1,矩形 ABCD 中,AB=10,BC=8.E 为边 BC 上一点,沿直线 DE 将矩形折.叠,使点C落在AB 边的点C'处.
(1)填空:AC'的长为 ;
(2)如图2,将△DC'E 沿线段AB 向右平移,使点 C'与点 B 重合,得到△D'BE',D'E'与 BC 交于点 F, D'B 与 DE 交于点G,求 EF 的长;
(3)在图 2 中,连接 GF,EE',则四边形GEE'F是平行四边形吗 若是,请予以证明;若不是,请说明理由.
3.已知抛物线 关于y轴对称,且过点((1, 和点(2,1).);
(1)求抛物线的解析式;
(2)若点 D(-1,p)和点 E(m-1,q)在抛物线上,试比较 p,q的大小;
(3)过点 F(0,1)作与y轴不垂直的直线交抛物线于点 A 和点 B,线段 AB 的垂直平分线交y轴于点M,试探 究 是否为定值 若是,求出定值;若不是,请说明理由.
4.如图1,在矩形 ABCD中,AB=8,BC=6,点 P 为线段CD 上的一个动点,点P 从D 点出发,以每秒4 个单位长度的速度从点 D 向点C 运动,过点 P 作AC 的平行线交 AD 于点 Q,将△PDQ 沿 PQ 折叠,点 D 落在点 E 处,连接 DE,AE,如图2,设运动的时间为 t秒.
(1)观察猜想:①当点 P 运动时,∠ADE的大小是否发生变化 若发生变化,求sin∠ADE的变化范围;若不发生变化,直接写出 sin∠ADE的值;
②在 P 点运动过程中,线段 AE 的最小值为 (直接写出答案);
(2)推理探究:设△PQE 与△ACD 的重叠部分的面积为S,请你直接写出 S与t 的函数解析式,并写出自变量 t的取值范围;
(3)拓展延伸:延长PE交直线AC 于点F,交直线 BA 于点G,在运动过程中,当F 为EG 的中点时(如图3),试求出 t的值.
5.如图1,M是线段 AB 上任意一点(不与点 A,B 重合),分别以 AM 和BM 为斜边在AB 同侧构造等腰直角三角形 AMC 和等腰直角三角形BMD,连接CD.取AB的中点E,CD的中点F,连接EF.
猜想验证:
(1)如图2,当点 M 与点 E 重合时,试判断EF 与CD 之间的数量关系,并说明理由;
(2)如图3,当点 M 与点 E 不重合时,问题
(1)中的结论是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由;
(3)如图3,若 AB=2cm ,线段 EF 是否存在最小值,若存在,请直接写出最小值;若不存在,请说明理由.
6.在学习研究完特殊的平行四边形之后,某学习小组针对矩形中的折叠问题进行了研究.问题背景如下:在矩形 ABCD 中,AB=4,BC=6. M为BC 的中点,P,Q分别是AB,CD边上的点,连接MP,MQ.
操作与发现
如图1,将△MBP 沿 PM 翻折,点 B 落在点 B'处,将△MCQ沿MQ 翻折,点 C 落在点C'处,连接 B'C'.
(1)当 B'C'∥BC时,小组成员发现 BP=CQ,请你完成证明;
(2)如图2,小组成员进一步发现当 MB'⊥MC',CQ=1时,还能求出 BP 的值,请你求出这个值;
(3)如图3,小组成员沿着(2)小题的思路,提出了问题“当△MB'C'为等边三角形,且CQ=1.5时,求 BP 的长”.请你直接写出BP 的长.
7.如图1,已知抛物线 与x轴交于A,B两点(点A 在点 B 的左侧),与 y轴交于点C,作直线 BC,点 C关于x轴的对称点是点C'.
(1)求点 C'的坐标和直线 BC 的表达式;
(2)如图2,点M 在抛物线的对称轴上,N为平面内一点,依次连接 BM,C'M,C'N,NB,当四边形 BMC'N 是菱形时,求点 M坐标;
(3)如图 3,P是抛物线第一象限内一动点,过点 P 作x 轴的平行线分别交直线BC 和 y 轴于点Q 和点E,连接 PC'交直线BC于点 D,连接 QC',PB,设点 P 的横坐标为m,△QC'D 的面积为S ,△PBD 的面积为S ,求 的最大值.
类型9 探究性问题
1.问题探究(1) (2)略 问题拓展
问题探究(1)证明∠ADF=∠CDE=∠CED=30°,从而证明AF:AD=AD:AB=1:2,即可得AFA;(2)取 BC的中点 H,连接 DH,证明△DBH≌△DEC,△EDH∽△EFB,再由相似三角形的性质证明结论;问题拓展利用全等三角形、相似三角形的判定与性质即可证明.
解:问题探究 (1)
(2)证明:取 BC的中点 H,连接DH.
∵D是AC的中点,
∵AB=AC,
∴DH=DC,
∴∠DHC=∠DCH.
∵BD=DE,
∴∠DBH=∠DEC.
∴∠BDH=∠EDC.
∴△DBH≌△DEC.
∴BH=EC.
∵DH∥AB,
∴△EDH∽△EFB.
另解1:证明∠ADF=∠ABD,得△ADF∽△ABD 也可求解.
另解2:取 AB的中点M,证明△ECD≌△DMB也可以求解.
问题拓展
2.(1)A(-2,0),B(8,0),C(0,4) y= (2)(4,6)(3)4或
(1)根据抛物线的函数表达式求出点 C,A,B的坐标,再利用待定系数法求出直线 BC的函数表达式即可;(2)易得点 过点 C 作CG⊥PD 于点G,由题中已知条件可证得四边形CODG是矩形,再利用矩形的性质与平行线的性质得到∠1=∠2,结合∠CGE=∠BOC,可证得△CGE∽△BOC,从而可求出EG,根据等腰三角形“三线合一”可得 PG=EG,然后利用 PD=PG+DG建立关于m 的方程,解方程即可求出m的值,据此可得点 P 的坐标;(3)过点 C作CH⊥PD于点 H,易得点 先求出直线AC的函数表达式,根据 PF∥AC,可得直线 PF 的函数表达式,从而可得点 F的坐标,求出 OF 的长,利用 HL定理证明Rt△CHE≌Rt△DOF,则有∠ECH=∠FDO,进而得∠FDO=∠CBO,利用等角的正切相等,可建立关于 m的方程,解方程即可求出 m的值.
解:(1)由 得,
当x=0时,y=4.
∴点C的坐标为(0,4).
当y=0时,
解,得.
∵点 A 在点 B 的左侧,
∴点 A,B的坐标分别为A(-2,0),B(8,0).
直线 BC的函数表达式为
(2)∵点 P 在第一象限抛物线上,横坐标为 m,且 PD⊥x轴于点 D,
∴点 P 的坐标为
∵点 B的坐标为(8,0),点 C的坐标为(0,4),
∴OB=8,OC=4.
过点C作CG⊥PD于点G,则∠CGD=90°.
∵∠PDO=∠COD=90°,
∴四边形 CODG 是矩形.
∴CG∥OB,DG=OC=4,CG=OD=m.
∴∠1=∠2.
∵∠CGE=∠BOC=90°,
∴△CGE∽△BOC.
即
在△CPE中,∵CP=CE,CG⊥PE,
解,得 (舍去).
∴m=4.
当m=4时,
∴点 P 的坐标为(4,6).
(3)m的值为4或:
3.(1) ∠ABP 或 ∠PBM 或 ∠MBC 或∠BME (2)①15,15②∠MBQ=∠CBQ,理由略 或
(1)过点 M作MH⊥BC于点 H,则易证四边形 BEMH是矩形,则 MH=BE,根据折叠的性质可知∠ABP= ,再利用正弦的定义可得 sin∠MBH 的值,从而可得∠MBC=30°,结合∠ABC=90°,可得∠ABP=∠PBM=30°,从而可得∠BME=30°;(2)①根据(1)中结论可得 根据 HL 证明 Rt△MBQ≌Rt△CBQ,从而即可求解;②根据正方形的性质与轴对称的性质得到对应边相等、对应角相等,再根据 HL证明 Rt△MBQ≌Rt△CBQ,从而即可得结论;(3)分点 Q在线段DF 上、线段 CF 上两种情况进行讨论,根据折叠的性质、勾股定理即可求解.解:(1)∠ABP 或∠PBM 或∠MBC 或∠BME.(注:任意写出一个即可)
(2)①15,15.
②∠MBQ=∠CBQ.
(注:若没有写出判断结果,但后续证明正确,不扣分)
理由如下:
∵四边形ABCD 是正方形,
∴AB=BC,∠A=∠C=90°.
由轴对称性质,得 BM=AB,∠BMP=∠A=90°.
∴∠BMQ=∠C=90°,BM=BC.
∵BQ是公共边,
∴Rt△MBQ≌Rt△CBQ.
∴∠MBQ=∠CBQ.
或2413cm.
4.(1)①略②1(2)m (3)
(1)①延长AD交BE于F,由折叠和等角的余角相等即可证明结论;②根据已知条件证明△ADC≌△BEC,即可求解;(2)延长AD交BE 于F,根据折叠和等角的余角相等证明两个角相等,并结合已知相等的角,证明△ACG∽△BCE,得比例式,即可求解;(3)根据折叠的性质,结合点 D 是BC 的中点得三角形的中位线,根据平行得同位角相等、内错角相等,再利用(2)中的相似三角形得对应边成比例,从而求出 AC 和CD 的比值,即可求出 CG 和AG 的比值,设CG=x,再根据比例式、三角形全等、勾股定理,表示出各边的长,根据EB·EH=6,求出x的值,取正值即可求解.
解:(1)①证明:延长AD交BE 于点 F.
由折叠得
∴∠DAC+∠ADC=∠BDF+∠EBC=90°.
∵∠ADC=∠BDF,
∴∠DAC=∠EBC.
理由:延长AD交BE 于点 F.
由折叠得
∴∠ADC+∠DAC=∠BDF+∠CBE=90°.
∵∠ADC=∠BDF,
∴∠DAC=∠CBE.
∵∠ACG=∠BCE,
∴△ACG∽△BCE.
(3)由折叠得∠AFB=90°,BF=FE.
∵D是BC 的中点,
∴DF∥CE.
∴∠BEC=∠BFD=90°,∠AGC=∠ECG,∠GAH=∠CEA.
由(2)知△ACG∽△BCE,
∴∠AGC=∠BEC=90°,
设CG=x,则
∴AG=CE.
∴△AGH≌△ECH.
∴AH=EH,GH=CH.
在 Rt△AGH中,
由勾股定理得
∵EB·EH=6,
解得 (负值舍去).
5.(1)EF=BF (2)AG=BG,证明略
(1)证法一:分别延长AD,BF 交于点M,根据平行四边形的性质可得对应角相等,结合中点得对应边相等,可证△MDF≌△BCF,得对应边相等,再利用直角三角形的斜边上的中线等于斜边的一半进行代换,可证明EF=BF;证法二:过点 F作 FM⊥EB于点 M,由已知条件结合平行线的判定得AD∥FM∥BC,由平行线分线段成比例定理,得出 EM=MB,进而由线段垂直平分线的性质得EF=BF;(2)证法一:根据折叠得对应角相等和对应边相等,结合中点和已知角相等进行代换,可证明四边形DGBF是平行四边形,等量代换后可证明AG=BG;证法二:连接CC'交 FB 于点 N,根据折叠的性质得 C'C⊥FB,根据平行线的判定得 DG∥FB,进而证得四边形DGBF是平行四边形,进而得出 AG=BG;(3)过点 M 作MP⊥BH 于点 P,由折叠的性质得△BPM是等腰直角三角形,根据 得 BH的长,进而可求出 A'H的长,通过证明△A'HN∽△CHB 得 NH 的长,再证△A'HN∽△A'PM,进而求得 HP,MP 的长,即可求出阴影部分的面积.
解:(1)EF=BF.
证法一:如图①,分别延长AD,BF相交于点 M.
∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠2=∠C,∠M=∠1.
∵F为CD的中点,∴DF=CF.
∴△MDF≌△BCF.
∴FM=FB.即 F为BM 的中点.
∵BE⊥AD,∴∠BEM=90°.
∴在 Rt△BEM中.
证法二:如图①,过点 F 作FM⊥EB于点 M,
则∠EMF=90°.
∵BE⊥AD,∴∠AEB=90°.
∴∠AEB=∠EMF.∴AD∥FM.
∵四边形ABCD 是平行四边形,∴AD∥BC.
∵F为CD 的中点,∴DF=FC.
∴EM=MB.
∵FM⊥EB,∴FM垂直平分EB.∴EF=BF.
(2)AG=BG.
证法一:如图②,
由折叠可知:
∵F为CD的中点,
∴FC'=FD.∴∠3=∠4.
∴∠4=∠1.∴DG∥FB.
∵四边形ABCD为平行四边形,∴DC∥AB.
∴四边形 DGBF 为平行四边形.
证法二:连接CC'交FB 于 N.
由折叠可知:FC'=FC,CC'⊥FB.
∵F为CD 的中点,
∵FC'=FC.∴∠FC'C=∠FCC'.在△DC'C中,
∴2∠2+2∠FC'C=180°.
∴∠2+∠FC'C=90°.∴∠DC'C=90°.
∴∠DC'C=∠C'NB.∴DG∥FB.
∵四边形 ABCD是平行四边形,∴DC∥AB.
∴四边形 DGBF 是平行四边形.
(3)
过点 M作MP⊥BH 于点 P,在 ABCD中,AB∥DC.
∵A'B⊥DC,∴A'B⊥AB,
由折叠可知∠ABM=∠MBH=45°,
∴△PBM是等腰直角三角形,∴PM=PB.
又 S□ABCD=BH·DC=5BH=20,∴BH=4.
由折叠知A'B=AB=5,∴A'H=1.
在 Rt△BCH 中, 由勾股定理可得CH=2.
由∠A'=∠C,∠A'HN=∠BHC=90°,可得△A'HN∽△CHB,. 即
又由 DC∥MP得△A'HN∽△A'PM,
设 HP=x,则A'P=1+x,BP=MP=4-x,
解得
即阴影部分的面积为
压轴预测
1.操作一:(1)40 (2)2 -2 操作二:
操作一:(1)由四边形 ABCD 是矩形得 CD ∥AB,∠DAE= 90°, 由 翻 折 得∠CEF = ∠CEB = 70°, 则∠AED=40°,所以∠EDC=∠AED=40°;(2)设BE=x,根据折叠的性质与矩形的性质得到对应边与对应角相等,根据CD∥AB 证明△DFC∽△EFA,根据相似三角形对应边成比例,可建立方程求出x的值,从而可得 BE的长;操作二:连接DG,根据三角形三边关系可知 DF>DG-FG,当点 F 落在DG 上时,线段 DF=DG-FG,即DF≥DG-FG,根据勾股定理求得 DG的长,即可得 DF的最小值.
解:操作一:(1)40
(2)设 BE=x,
由折叠得∠CED=∠CEB,EF=BE=x,在矩形 ABCD中,CD=AB=x+4,CD∥AB,
∴∠CEB=∠DCE,
∴∠CED=∠DCE,∴CD=DE,
∴DE=AB,
∴DE-EF=AB-BE,即 DF=AE=4.
∵CD∥AB,∴△DFC∽△EFA,
解得 (舍),
∴BE=2 -2.
操作二:
2.(1)6 (2)2 (3)四边形GEE'F 不是平行四边形,理由略
(1)由△AC'D为直角三角形,利用勾股定理建立方程求得AC'的长;(2)由勾股定理求得 BE,连接 EE',由平移的性质、相似三角形的判定和性质求得 EF;(3)作辅助线,由相似三角形的性质、勾股定理、等腰三角形的性质计算出 D'F 与 DG 的长度,从而得到 GE 与 FE'的长度关系,根据平行四边形的判定进行判断.
解:(1)6.
(2)由折叠可知,DC'=DC=10.
在 Rt△DAC'中,根据勾股定理可求得 AC'=6,
∴BC'=AB-AC'=10-6=4.
在 Rt△BEC'中,设BE=x,
根据勾股定理,得(
解得x=3,即BE=3,EC'=EC=5.
连接EE',则由平移可知,
EE'=C'B=4,且EE'∥AB∥CD,
于是可得△FEE'∽△FCD'∽△ECD,
∴EF:EE'=CE:CD=5:10=1:2.
又EE'=4,∴EF=2.
(3)四边形GEE'F 不是平行四边形.
理由如下:
由折叠可知∠CDE=∠C'DE.
另由平移可知∠C'DE=∠BD'E',且 DE∥D'E',于是得∠BD'E'=∠D'GD,
∴∠CDE=∠D'GD,即△DD'G 是等腰三角形,∴DD'=D'G=4.
如图,过点 D'作D'H⊥DG 于点 H,
则 DH=HG,且△DD'H∽△DEC,
则D'H:DH=EC:DC=1:2.
设D'H=x,则 DH=2x.
在 Rt△DD'H 中,根据勾股定理,
得 解得
而在Rt△D'CF中,D'C=DC-DD'=10-4=6,
CF=CE-EF=5-2=3,
根据勾股定理可求得D'F=3
∴DG≠D'F,即GE≠FE',
故四边形GEE'F不可能是平行四边形.
(2)当m=0或m=2时,p=q;当m<0或m>2时,pq (3)2
(1)根据抛物线关于y轴对称可确定b的值,再根据已知两点求出a,c的值,即可求出抛物线的解析式;(2)先求出点 D及其关于y轴的对称点的坐标,再根据抛物线的开口方向和对称轴确定横坐标的关系,列出方程或不等式,求出 m的值,从而分情况比较出 p和q的大小即可;或由 得p-q关于m 的函数,进而即可求解;或根据二次函数的图象与性质直接求解即可;(3)设定点A,B的坐标及直线AB 的解析式,将其代入抛物线解析式,得到一元二次方程,求出方程的解(含待定系数k),即可分别求出自变量以及函数值的和或差,再利用勾股定理、相似三角形的判定与性质即可求解;或设出 A,B两点坐标及直线AB 的解析式,将直线 AB 的解析式代入 中,得关于x的一元二次方程,得方程的解再设AB的垂直平分线上的任意一点Q(x,y),再由勾股定理进而即可求解.
解:(1)∵抛物线关于 y轴对称,∴b=0.
又∵抛物线过点(1, ),(2,1),
解得
∴抛物线的解析式为
(2)解法一:∵点 D(-1,p)在抛物线 上,
∵抛物线图象开口向上,且点 关于y轴的对称点的坐标为((1, ),
∴由图象可知,
当m-1=1或m-1=-1,即当m=2或m=0时,p=q;当m-1<-1或m-1>1,即当m<0或m>2时,pq,
∴当m=0或m=2时,p=q;当m<0或m>2时,pq.
解法二:
把 p-q看成关于m的函数,由图象可知,
当m=0或m=2时,p=q;
当m<0或m>2时,p当0q.
解法三:二次函数 开口向上,对称轴为y轴,
∴抛物线 上距离 y轴越远的点,函数值越大.
∵点 D到y 轴距离为1,
∴由图象可知,
当m-1=±1,即m=0或m=2时,p=q;
当m-1<-1或m-1>1,即m<0或m>2时,p当--1q.
(3)解法一: 为定值,且定值是2.
设A(x ,y ),B(x ,y ),直线 AB的解析式为y= kx+1(k≠0).
把y= kx+1代入 中,得
则
如图,过点 B 作 BN⊥y轴,过点 A 作 AN∥y轴,交点为 N.
线段 AB中点 P 的坐标为(2k,2k +1).
又∵F(0,1),根据勾股定理,可得
∵∠MPF=∠BNA=90°,∠MFP=∠BFO=∠BAN,
∴△FPM∽△ANB,
解法.二: 为定值,且定值是2.
设A(x ,y ),B(x ,y ),直线 AB的解析式为y= kx+1(k≠0).
把y= kx+1代.入 中,得
则
设AB的垂直平分线上的任意一点Q 的坐标为(x,y).
根据勾股定理,可得
整理得
令x=0,得 即M(0,2k +3),
根据勾股定理,可得
4. (1) ① ② (2) S =
(1)①由已知条件得∠ADE=∠ACD,从而判断出∠ADE不发生变化并求得 sin∠ADE;②当 AE⊥DE时, 即可求解;(2)当0≤t≤1时, 当1解:(1)①由题意知 PQ为DE 的中垂线,由 PQ∥AC知直线 DE始终与AC 垂直,∴∠ADE=∠ACD,
∴∠ADE的大小不会发生变化,
②线段 AE的最小值为
(2)由题意知PD=4t,PC=8-4t,当点 E刚好落在AC上时,P为CD 的中点,如图1,
∴4t=4,∴t=1.
当0≤t≤1时, 当1设 EQ,PE分别交AC 于点 N,M.
由折叠知∠1=∠2.
∵PQ∥AC,∴∠1=∠4,∠2=∠3,
∴∠3=∠4,∴PC=PM=8-4t,∴EM=8t-8.
同理(QN=QA=6-3t,EN=6t-6,
(3)如图3,由题意知PD=PE=4t,PC=PF=8-4t,∴EF=FG=GA=8-8t,∴PG=16-12t.
过点G作GH⊥CD于点 H,
则DH=8-8t,PH=12t-8,
∴在 Rt△GPH中, 解得
5.(1)CD=2EF,理由略 (2)成立,证明略(3)
(1)利用直角三角形斜边中线的性质证明即可;(2)延长AC交BD 的延长线于点G,连接GM,GE,利用矩形的性质,直角三角形斜边中线的性质求解即可;(3)根据CD=2EF,CD=MG≥EG求解 EF 的最小值.
解:(1)CD=2EF.
理由如下:
∵△AMC 和△BMD都是等腰直角三角形,
∴∠ACM=∠MDB=90°,AC=MC,MD=BD,
∴∠CMD=180°-∠AMC-∠DMB=90°.
∵F是CD 的中点,
即CD=2MF.
∵点 M 与点 E 重合,
∴MF=EF,∴CD=2EF.
(2)成立.
证明:如图,延长 AC 交 BD 的延长线于点 G,连接GM,GE.
∵△AMC 和△BMD都是等腰直角三角形,
∴∠ACM=∠MDB=90°,AC=MC,MD=BD,
∴∠MCG=∠AGB=∠GDM=90°,AG=BG,
∴四边形 MCGD是矩形,△AGB是等腰直角三角形,
∴GM=CD.
∵E是AB 的中点,∴GE⊥AB,
∵F是CD 的中点,∴F 是GM 的中点.
在 Rt△MEG中,F是GM 的中点,
即CD=2EF.
(3)
6.(1)略 (2)
(1)由等边对等角得. ,由 B'C'∥BC得. ,再利用等腰
三角形两底角相等和折叠的性质得到∠BMP=∠CMQ,通过三角函数的定义可证得BP=CQ;(2)延长 PM与DC,延长线交于点E,作QF⊥ME于点F,由折叠及对顶角相等可得∠QME=45°,在 Rt△CMQ中,利用勾股定理求出MQ的长,设 BP=x,易证得△CME≌△BMP,表示出QE,QF,ME 的长,再利用等面积法列方程解出x的值,即可得到 BP 的长度;(3)延长 QM 交AB 的延长线于点H,作 PN⊥MH 于点 N.由折叠及对顶角相等可得∠PMH=60°,在 Rt△CMQ 中,利用勾股定理求出 MQ的长,设 BP=x,易证得△CMQ≌△BMH,表示出 PN,MH,PH的长,再利用等面积法列方程解出x的值,即可得到 BP的值.
解:(1)证明:∵M为BC的中点,∴MB=MC.
由折叠知B'M=BM,C'M=CM,
∵B'C'∥BC,
由折叠可知,
∴∠BMP=∠CMQ.
∵四边形ABCD是矩形,∴∠B=∠C=90°.
在 Rt△BMP 和 Rt△CMQ中可得,
∵MB=MC,∠BMP=∠CMQ,∴BP=CQ.
(2)如图所示,延长 PM与DC,延长线交于点 E,作 QF⊥ME于点 F.
∵MB'⊥MC',
再由折叠及对顶角相等可得∠QME=45°.
∵BC=6,M是BC 的中点,
∴BM=CM=3.
在 Rt△CMQ中,由勾股定理得
设BP=x,在 Rt△BPM中,由勾股定理得
在△CME 和△BMP中,
∵∠CME=∠BMP,CM=BM,
∠MCE=∠MBP=90°,
∴△CME≌△BMP,
在 Rt△MFQ中,∵∠QME=45°,MQ=
由 可得MC ·QE =FQ ·ME ,
解得 (不符合题意,舍去),
∴BP的长为
延长 QM 交 AB 的延长线于点 H,作 PN⊥MH 于点 N.
∵△C'MB'是等边三角形,
再由折叠及对顶角相等可得∠PMH=60°.
∵BC=6,M是BC 的中点,
∴BM=CM=3.
在 Rt△CMQ中,由勾股定理可得
设BP=x,在Rt△BPM中,由勾股定理得
在△CMQ 和△BMH中,
∵∠CMQ=∠BMH,CM=BM,∠MCQ=∠MBH=90°,
∴△CMQ≌△BMH,
在 Rt△PMN中,∵∠PMN=60°,PM=√x +9,
由 可得 PH ·
BM =HM ·PN ,
解得 不符合题意,舍去),
∴BP的长为
7.(1)C'(0,-4) y=-x+4 (2)(1,--1)(3)4
(1)对于抛物线解析式,令y=0,求得x的值,即可得点 B坐标,令x=0,可得到点C的坐标,利用待定系数法求得直线 BC 的解析式;(2)取 BC'的中点G,连接OG 交抛物线的对称轴于点M,过点 M 作 MH⊥y轴于点 H,根据已知条件证得OH=MH,由对称轴 得到 HM的长,从而得到点 M 的坐标;(3)过点 B 作 BI⊥PQ 于点Ⅰ,由已知条件得四边形 EOBI是矩形,证得 BI=OE,从而得到. ,根据点 P 在抛物线上,点Q 在直线 BC 上,得到点 P,Q的坐标,从而得到线段 PQ关于m 的二次函数的顶点式,即可求解.
解:(1)∵抛物线与x轴相交于点A,B,
当y=0时,
解得
∴B(4,0).
∵抛物线与 y轴相交于点C,
当x=0时,y=4,
∴C(0,4),∴C'(0,-4).
设 BC的表达式为y= kx+b,
将 B,C两点坐标分别代入得
解得
∴直线 BC的表达式为y=-x+4.
(2)取 BC'的中点G,连接OG 交抛物线的对称轴于点M,此时四边形 BMC'N 是以 BC'为对角线的菱形,过点 M作MH⊥y轴于点 H.
∴∠OMH=45°,
∴∠C'OG=∠OMH,
∴OH=MH.
∵抛物线的对称轴为直线
∴OH=MH=1,
∴M(1,-1).
(3)过点 B作BI⊥PQ于点I.
∵PQ∥x轴,∴∠IEO=90°.
∵∠IEO=∠EOB=∠BIE=90°,
∴四边形 EOBI是矩形,∴BI=OE,
=2QP.
∵点 P 在抛物线上,且点 P 的横坐标为m,
∴点 P 的纵坐标为
∵PQ∥x轴,
∴点 Q的纵坐标为 将其代入y=-x+4中,得点 Q的横坐标为
∵P是抛物线第一象限内一动点,
∴点 P 在点Q 右侧,
∴当m=2时,PQ的最大值是2.
的最大值是4.
压轴例题精讲
【例】有公共顶点 A 的正方形ABCD 与正方形AEGF 按如图1 所示放置,点 E,F 分别在边 AB 和AD 上,连接 BF,DE,M 是 BF 的中点,连接 AM 交DE 于点 N.
(1)线段 DE 与 AM 之间的数量关系是 ,位置关系是 ;
(2)将图1中的正方形AEGF 绕点 A 顺时针旋转 45°,点 G 恰好落在边 AB 上,如图2,其他条件不变,线段 DE 与AM 之间的关系是否仍然成立 并说明理由.
【解】(1)DE=2AM DE⊥AM.
(2)仍然成立.理由如下:
如图,延长 AM 到点 H,使 MH=AM,连接BH.
∵点 M是BF 的中点,∴BM=FM.
又∠BMH=∠AMF,
∴△BHM≌△FAM,
∴BH=AF=AE,∠H=∠FAM,
∴AF∥BH,
∴∠FAB+∠ABH=180°.
又∵ ∠EAF + ∠BAD = ∠DAE +∠BAF=180°,
∴∠ABH=∠DAE.又AB=AD,
∴△ABH≌△DAE,∴AH=DE.
∵AH=2AM,∴DE=2AM.
又 ∠BAH = ∠ADE, ∠BAH +∠DAN=90°,
∴∠ADE+∠DAN=90°,
∴∠AND=90°,
中小学教育资源及组卷应用平台
即 DE⊥AM.
1.问题提出 如图1,在△ABC中,AB=AC,D是AC 的中点,延长 BC至点 E,使 DE = DB,延长 ED 交 AB 于点F,探究 的值.
问题探究 (1)先将问题特殊化.如图2,当∠BAC=60°时,直接写出 的值;
(2)再探究一般情形.如图1,证明(1)中的结论仍然成立.
问题拓展 如图3,在△ABC 中,AB=AC,D 是AC 的中点,G是边BC 上一点, 延长 BC至点E,使 DE=DG,延长 ED交AB 于点 F.直接写出 的值(用含 n的式子表示).
2.如图,二次函数 的图象与x轴交于A,B 两点(点 A 在点 B 的左侧),与y轴交于点 C.点P 是第一象限内二次函数图象上的一个动点,设点 P 的横坐标为m.过点 P 作直线 PD⊥x轴于点D,作直线 BC交 PD 于点 E.
(1)求A,B,C三点的坐标,并直接写出直线 BC的函数表达式;
(2)当△CEP 是以 PE 为底边的等腰三角形时,求点 P 的坐标;
(3)连接 AC,过点 P 作直线l∥ AC,交y轴于点 F,连接 DF.试探究:在点 P 运动的过程中,是否存在点 P,使得CE=FD,若存在,请直接写出 m的值;若不存在,请说明理由.
3.综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片 ABCD,使 AD 与BC 重合,得到折痕 EF,把纸片展平;
操作二:在 AD 上选一点 P,沿 BP 折叠,使点 A 落在矩形内部点 M 处,把纸片展平,连接 PM,BM.
根据以上操作,当点 M 在 EF 上时,写出图1中一个30°的角: ;
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长 PM交CD 于点Q,连接 BQ.
①如图2,当点 M 在 EF 上时,∠MBQ= °,∠CBQ= °;
②改变点 P 在 AD 上的位置(点 P 不与点A,D 重合),如图 3,判断∠MBQ 与∠CBQ的数量关系,并说明理由;
(3)拓展应用
在(2)的探究中,已知正方形纸片 ABCD的边长为8cm,当FQ=1 cm时,直接写出AP 的长.
4.在△ABC中,∠ACB= D是边BC上一点,将△ABD沿AD 折叠得到△AED,连接 BE.
(1)特例发现 如图1,当m=1,AE落在直线AC上时,
①求证:∠DAC=∠EBC;
②填空: 的值为 ;
(2)类比探究 如图2,当 m≠1,AE与边BC 相交时,
在 AD 上取一点G,使∠ACG=∠BCE,CG交 AE 于点 H.探究( 的值(用含m的式子表示),并写出探究过程;
(3)拓展运用 在(2)的条件下,当 D是BC 的中点时,若EB·EH=6,求 CG的长.
5.问题情境:数学活动课上,老师出示了一个问题:如图①,在□ABCD中,BE⊥AD,垂足为 E,F为CD 的中点,连接EF,BF,试猜想 EF 与BF 的数量关系,并加以证明;
独立思考:(1)请解答老师提出的问题;
实践探究:(2)希望小组受此问题的启发,将 ABCD沿着 BF(F 为CD 的中点)所在直线折叠,如图②,点C 的对应点为C',连接DC'并延长交AB 于点G,请判断AG与 BG 的数量关系,并加以证明;
问题解决:(3)智慧小组突发奇想,将□ABCD沿过点 B 的直线折叠,如图③,点 A 的对应点为 A′, 使 A′B⊥CD 于点 H,折痕交 AD 于点M,连接 A'M,交CD 于点 N.该小组提出一个问题:若此□ABCD的面积为20,边长AB=5,BC= ,求图中阴影部分(四边形 BHNM)的面积.请你思考此问题,直接写出结果.
1.实验与探究
操作一:如图1是一张矩形纸片,点E 在边AB上,把△BCE 沿直线CE 翻折,使点 B落在对角线AC 上的点 F 处,连接 DF,且点 E,F,D在同一直线上.
(1)若∠CEB=70°,则∠EDC= °;
(2)当AE=4时,求 BE的长.
操作二:如图2,矩形纸片中,AB=5,BC=4,点G是 BC 的中点,点 E 是AB 边上的一动点,将△BGE沿EG 所在直线翻折得到△FEG,连接 DF,则线段 DF 的最小值是 .
2.如图1,矩形 ABCD 中,AB=10,BC=8.E 为边 BC 上一点,沿直线 DE 将矩形折.叠,使点C落在AB 边的点C'处.
(1)填空:AC'的长为 ;
(2)如图2,将△DC'E 沿线段AB 向右平移,使点 C'与点 B 重合,得到△D'BE',D'E'与 BC 交于点 F, D'B 与 DE 交于点G,求 EF 的长;
(3)在图 2 中,连接 GF,EE',则四边形GEE'F是平行四边形吗 若是,请予以证明;若不是,请说明理由.
3.已知抛物线 关于y轴对称,且过点((1, 和点(2,1).);
(1)求抛物线的解析式;
(2)若点 D(-1,p)和点 E(m-1,q)在抛物线上,试比较 p,q的大小;
(3)过点 F(0,1)作与y轴不垂直的直线交抛物线于点 A 和点 B,线段 AB 的垂直平分线交y轴于点M,试探 究 是否为定值 若是,求出定值;若不是,请说明理由.
4.如图1,在矩形 ABCD中,AB=8,BC=6,点 P 为线段CD 上的一个动点,点P 从D 点出发,以每秒4 个单位长度的速度从点 D 向点C 运动,过点 P 作AC 的平行线交 AD 于点 Q,将△PDQ 沿 PQ 折叠,点 D 落在点 E 处,连接 DE,AE,如图2,设运动的时间为 t秒.
(1)观察猜想:①当点 P 运动时,∠ADE的大小是否发生变化 若发生变化,求sin∠ADE的变化范围;若不发生变化,直接写出 sin∠ADE的值;
②在 P 点运动过程中,线段 AE 的最小值为 (直接写出答案);
(2)推理探究:设△PQE 与△ACD 的重叠部分的面积为S,请你直接写出 S与t 的函数解析式,并写出自变量 t的取值范围;
(3)拓展延伸:延长PE交直线AC 于点F,交直线 BA 于点G,在运动过程中,当F 为EG 的中点时(如图3),试求出 t的值.
5.如图1,M是线段 AB 上任意一点(不与点 A,B 重合),分别以 AM 和BM 为斜边在AB 同侧构造等腰直角三角形 AMC 和等腰直角三角形BMD,连接CD.取AB的中点E,CD的中点F,连接EF.
猜想验证:
(1)如图2,当点 M 与点 E 重合时,试判断EF 与CD 之间的数量关系,并说明理由;
(2)如图3,当点 M 与点 E 不重合时,问题
(1)中的结论是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由;
(3)如图3,若 AB=2cm ,线段 EF 是否存在最小值,若存在,请直接写出最小值;若不存在,请说明理由.
6.在学习研究完特殊的平行四边形之后,某学习小组针对矩形中的折叠问题进行了研究.问题背景如下:在矩形 ABCD 中,AB=4,BC=6. M为BC 的中点,P,Q分别是AB,CD边上的点,连接MP,MQ.
操作与发现
如图1,将△MBP 沿 PM 翻折,点 B 落在点 B'处,将△MCQ沿MQ 翻折,点 C 落在点C'处,连接 B'C'.
(1)当 B'C'∥BC时,小组成员发现 BP=CQ,请你完成证明;
(2)如图2,小组成员进一步发现当 MB'⊥MC',CQ=1时,还能求出 BP 的值,请你求出这个值;
(3)如图3,小组成员沿着(2)小题的思路,提出了问题“当△MB'C'为等边三角形,且CQ=1.5时,求 BP 的长”.请你直接写出BP 的长.
7.如图1,已知抛物线 与x轴交于A,B两点(点A 在点 B 的左侧),与 y轴交于点C,作直线 BC,点 C关于x轴的对称点是点C'.
(1)求点 C'的坐标和直线 BC 的表达式;
(2)如图2,点M 在抛物线的对称轴上,N为平面内一点,依次连接 BM,C'M,C'N,NB,当四边形 BMC'N 是菱形时,求点 M坐标;
(3)如图 3,P是抛物线第一象限内一动点,过点 P 作x 轴的平行线分别交直线BC 和 y 轴于点Q 和点E,连接 PC'交直线BC于点 D,连接 QC',PB,设点 P 的横坐标为m,△QC'D 的面积为S ,△PBD 的面积为S ,求 的最大值.
类型9 探究性问题
1.问题探究(1) (2)略 问题拓展
问题探究(1)证明∠ADF=∠CDE=∠CED=30°,从而证明AF:AD=AD:AB=1:2,即可得AFA;(2)取 BC的中点 H,连接 DH,证明△DBH≌△DEC,△EDH∽△EFB,再由相似三角形的性质证明结论;问题拓展利用全等三角形、相似三角形的判定与性质即可证明.
解:问题探究 (1)
(2)证明:取 BC的中点 H,连接DH.
∵D是AC的中点,
∵AB=AC,
∴DH=DC,
∴∠DHC=∠DCH.
∵BD=DE,
∴∠DBH=∠DEC.
∴∠BDH=∠EDC.
∴△DBH≌△DEC.
∴BH=EC.
∵DH∥AB,
∴△EDH∽△EFB.
另解1:证明∠ADF=∠ABD,得△ADF∽△ABD 也可求解.
另解2:取 AB的中点M,证明△ECD≌△DMB也可以求解.
问题拓展
2.(1)A(-2,0),B(8,0),C(0,4) y= (2)(4,6)(3)4或
(1)根据抛物线的函数表达式求出点 C,A,B的坐标,再利用待定系数法求出直线 BC的函数表达式即可;(2)易得点 过点 C 作CG⊥PD 于点G,由题中已知条件可证得四边形CODG是矩形,再利用矩形的性质与平行线的性质得到∠1=∠2,结合∠CGE=∠BOC,可证得△CGE∽△BOC,从而可求出EG,根据等腰三角形“三线合一”可得 PG=EG,然后利用 PD=PG+DG建立关于m 的方程,解方程即可求出m的值,据此可得点 P 的坐标;(3)过点 C作CH⊥PD于点 H,易得点 先求出直线AC的函数表达式,根据 PF∥AC,可得直线 PF 的函数表达式,从而可得点 F的坐标,求出 OF 的长,利用 HL定理证明Rt△CHE≌Rt△DOF,则有∠ECH=∠FDO,进而得∠FDO=∠CBO,利用等角的正切相等,可建立关于 m的方程,解方程即可求出 m的值.
解:(1)由 得,
当x=0时,y=4.
∴点C的坐标为(0,4).
当y=0时,
解,得.
∵点 A 在点 B 的左侧,
∴点 A,B的坐标分别为A(-2,0),B(8,0).
直线 BC的函数表达式为
(2)∵点 P 在第一象限抛物线上,横坐标为 m,且 PD⊥x轴于点 D,
∴点 P 的坐标为
∵点 B的坐标为(8,0),点 C的坐标为(0,4),
∴OB=8,OC=4.
过点C作CG⊥PD于点G,则∠CGD=90°.
∵∠PDO=∠COD=90°,
∴四边形 CODG 是矩形.
∴CG∥OB,DG=OC=4,CG=OD=m.
∴∠1=∠2.
∵∠CGE=∠BOC=90°,
∴△CGE∽△BOC.
即
在△CPE中,∵CP=CE,CG⊥PE,
解,得 (舍去).
∴m=4.
当m=4时,
∴点 P 的坐标为(4,6).
(3)m的值为4或:
3.(1) ∠ABP 或 ∠PBM 或 ∠MBC 或∠BME (2)①15,15②∠MBQ=∠CBQ,理由略 或
(1)过点 M作MH⊥BC于点 H,则易证四边形 BEMH是矩形,则 MH=BE,根据折叠的性质可知∠ABP= ,再利用正弦的定义可得 sin∠MBH 的值,从而可得∠MBC=30°,结合∠ABC=90°,可得∠ABP=∠PBM=30°,从而可得∠BME=30°;(2)①根据(1)中结论可得 根据 HL 证明 Rt△MBQ≌Rt△CBQ,从而即可求解;②根据正方形的性质与轴对称的性质得到对应边相等、对应角相等,再根据 HL证明 Rt△MBQ≌Rt△CBQ,从而即可得结论;(3)分点 Q在线段DF 上、线段 CF 上两种情况进行讨论,根据折叠的性质、勾股定理即可求解.解:(1)∠ABP 或∠PBM 或∠MBC 或∠BME.(注:任意写出一个即可)
(2)①15,15.
②∠MBQ=∠CBQ.
(注:若没有写出判断结果,但后续证明正确,不扣分)
理由如下:
∵四边形ABCD 是正方形,
∴AB=BC,∠A=∠C=90°.
由轴对称性质,得 BM=AB,∠BMP=∠A=90°.
∴∠BMQ=∠C=90°,BM=BC.
∵BQ是公共边,
∴Rt△MBQ≌Rt△CBQ.
∴∠MBQ=∠CBQ.
或2413cm.
4.(1)①略②1(2)m (3)
(1)①延长AD交BE于F,由折叠和等角的余角相等即可证明结论;②根据已知条件证明△ADC≌△BEC,即可求解;(2)延长AD交BE 于F,根据折叠和等角的余角相等证明两个角相等,并结合已知相等的角,证明△ACG∽△BCE,得比例式,即可求解;(3)根据折叠的性质,结合点 D 是BC 的中点得三角形的中位线,根据平行得同位角相等、内错角相等,再利用(2)中的相似三角形得对应边成比例,从而求出 AC 和CD 的比值,即可求出 CG 和AG 的比值,设CG=x,再根据比例式、三角形全等、勾股定理,表示出各边的长,根据EB·EH=6,求出x的值,取正值即可求解.
解:(1)①证明:延长AD交BE 于点 F.
由折叠得
∴∠DAC+∠ADC=∠BDF+∠EBC=90°.
∵∠ADC=∠BDF,
∴∠DAC=∠EBC.
理由:延长AD交BE 于点 F.
由折叠得
∴∠ADC+∠DAC=∠BDF+∠CBE=90°.
∵∠ADC=∠BDF,
∴∠DAC=∠CBE.
∵∠ACG=∠BCE,
∴△ACG∽△BCE.
(3)由折叠得∠AFB=90°,BF=FE.
∵D是BC 的中点,
∴DF∥CE.
∴∠BEC=∠BFD=90°,∠AGC=∠ECG,∠GAH=∠CEA.
由(2)知△ACG∽△BCE,
∴∠AGC=∠BEC=90°,
设CG=x,则
∴AG=CE.
∴△AGH≌△ECH.
∴AH=EH,GH=CH.
在 Rt△AGH中,
由勾股定理得
∵EB·EH=6,
解得 (负值舍去).
5.(1)EF=BF (2)AG=BG,证明略
(1)证法一:分别延长AD,BF 交于点M,根据平行四边形的性质可得对应角相等,结合中点得对应边相等,可证△MDF≌△BCF,得对应边相等,再利用直角三角形的斜边上的中线等于斜边的一半进行代换,可证明EF=BF;证法二:过点 F作 FM⊥EB于点 M,由已知条件结合平行线的判定得AD∥FM∥BC,由平行线分线段成比例定理,得出 EM=MB,进而由线段垂直平分线的性质得EF=BF;(2)证法一:根据折叠得对应角相等和对应边相等,结合中点和已知角相等进行代换,可证明四边形DGBF是平行四边形,等量代换后可证明AG=BG;证法二:连接CC'交 FB 于点 N,根据折叠的性质得 C'C⊥FB,根据平行线的判定得 DG∥FB,进而证得四边形DGBF是平行四边形,进而得出 AG=BG;(3)过点 M 作MP⊥BH 于点 P,由折叠的性质得△BPM是等腰直角三角形,根据 得 BH的长,进而可求出 A'H的长,通过证明△A'HN∽△CHB 得 NH 的长,再证△A'HN∽△A'PM,进而求得 HP,MP 的长,即可求出阴影部分的面积.
解:(1)EF=BF.
证法一:如图①,分别延长AD,BF相交于点 M.
∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠2=∠C,∠M=∠1.
∵F为CD的中点,∴DF=CF.
∴△MDF≌△BCF.
∴FM=FB.即 F为BM 的中点.
∵BE⊥AD,∴∠BEM=90°.
∴在 Rt△BEM中.
证法二:如图①,过点 F 作FM⊥EB于点 M,
则∠EMF=90°.
∵BE⊥AD,∴∠AEB=90°.
∴∠AEB=∠EMF.∴AD∥FM.
∵四边形ABCD 是平行四边形,∴AD∥BC.
∵F为CD 的中点,∴DF=FC.
∴EM=MB.
∵FM⊥EB,∴FM垂直平分EB.∴EF=BF.
(2)AG=BG.
证法一:如图②,
由折叠可知:
∵F为CD的中点,
∴FC'=FD.∴∠3=∠4.
∴∠4=∠1.∴DG∥FB.
∵四边形ABCD为平行四边形,∴DC∥AB.
∴四边形 DGBF 为平行四边形.
证法二:连接CC'交FB 于 N.
由折叠可知:FC'=FC,CC'⊥FB.
∵F为CD 的中点,
∵FC'=FC.∴∠FC'C=∠FCC'.在△DC'C中,
∴2∠2+2∠FC'C=180°.
∴∠2+∠FC'C=90°.∴∠DC'C=90°.
∴∠DC'C=∠C'NB.∴DG∥FB.
∵四边形 ABCD是平行四边形,∴DC∥AB.
∴四边形 DGBF 是平行四边形.
(3)
过点 M作MP⊥BH 于点 P,在 ABCD中,AB∥DC.
∵A'B⊥DC,∴A'B⊥AB,
由折叠可知∠ABM=∠MBH=45°,
∴△PBM是等腰直角三角形,∴PM=PB.
又 S□ABCD=BH·DC=5BH=20,∴BH=4.
由折叠知A'B=AB=5,∴A'H=1.
在 Rt△BCH 中, 由勾股定理可得CH=2.
由∠A'=∠C,∠A'HN=∠BHC=90°,可得△A'HN∽△CHB,. 即
又由 DC∥MP得△A'HN∽△A'PM,
设 HP=x,则A'P=1+x,BP=MP=4-x,
解得
即阴影部分的面积为
压轴预测
1.操作一:(1)40 (2)2 -2 操作二:
操作一:(1)由四边形 ABCD 是矩形得 CD ∥AB,∠DAE= 90°, 由 翻 折 得∠CEF = ∠CEB = 70°, 则∠AED=40°,所以∠EDC=∠AED=40°;(2)设BE=x,根据折叠的性质与矩形的性质得到对应边与对应角相等,根据CD∥AB 证明△DFC∽△EFA,根据相似三角形对应边成比例,可建立方程求出x的值,从而可得 BE的长;操作二:连接DG,根据三角形三边关系可知 DF>DG-FG,当点 F 落在DG 上时,线段 DF=DG-FG,即DF≥DG-FG,根据勾股定理求得 DG的长,即可得 DF的最小值.
解:操作一:(1)40
(2)设 BE=x,
由折叠得∠CED=∠CEB,EF=BE=x,在矩形 ABCD中,CD=AB=x+4,CD∥AB,
∴∠CEB=∠DCE,
∴∠CED=∠DCE,∴CD=DE,
∴DE=AB,
∴DE-EF=AB-BE,即 DF=AE=4.
∵CD∥AB,∴△DFC∽△EFA,
解得 (舍),
∴BE=2 -2.
操作二:
2.(1)6 (2)2 (3)四边形GEE'F 不是平行四边形,理由略
(1)由△AC'D为直角三角形,利用勾股定理建立方程求得AC'的长;(2)由勾股定理求得 BE,连接 EE',由平移的性质、相似三角形的判定和性质求得 EF;(3)作辅助线,由相似三角形的性质、勾股定理、等腰三角形的性质计算出 D'F 与 DG 的长度,从而得到 GE 与 FE'的长度关系,根据平行四边形的判定进行判断.
解:(1)6.
(2)由折叠可知,DC'=DC=10.
在 Rt△DAC'中,根据勾股定理可求得 AC'=6,
∴BC'=AB-AC'=10-6=4.
在 Rt△BEC'中,设BE=x,
根据勾股定理,得(
解得x=3,即BE=3,EC'=EC=5.
连接EE',则由平移可知,
EE'=C'B=4,且EE'∥AB∥CD,
于是可得△FEE'∽△FCD'∽△ECD,
∴EF:EE'=CE:CD=5:10=1:2.
又EE'=4,∴EF=2.
(3)四边形GEE'F 不是平行四边形.
理由如下:
由折叠可知∠CDE=∠C'DE.
另由平移可知∠C'DE=∠BD'E',且 DE∥D'E',于是得∠BD'E'=∠D'GD,
∴∠CDE=∠D'GD,即△DD'G 是等腰三角形,∴DD'=D'G=4.
如图,过点 D'作D'H⊥DG 于点 H,
则 DH=HG,且△DD'H∽△DEC,
则D'H:DH=EC:DC=1:2.
设D'H=x,则 DH=2x.
在 Rt△DD'H 中,根据勾股定理,
得 解得
而在Rt△D'CF中,D'C=DC-DD'=10-4=6,
CF=CE-EF=5-2=3,
根据勾股定理可求得D'F=3
∴DG≠D'F,即GE≠FE',
故四边形GEE'F不可能是平行四边形.
(2)当m=0或m=2时,p=q;当m<0或m>2时,p
(1)根据抛物线关于y轴对称可确定b的值,再根据已知两点求出a,c的值,即可求出抛物线的解析式;(2)先求出点 D及其关于y轴的对称点的坐标,再根据抛物线的开口方向和对称轴确定横坐标的关系,列出方程或不等式,求出 m的值,从而分情况比较出 p和q的大小即可;或由 得p-q关于m 的函数,进而即可求解;或根据二次函数的图象与性质直接求解即可;(3)设定点A,B的坐标及直线AB 的解析式,将其代入抛物线解析式,得到一元二次方程,求出方程的解(含待定系数k),即可分别求出自变量以及函数值的和或差,再利用勾股定理、相似三角形的判定与性质即可求解;或设出 A,B两点坐标及直线AB 的解析式,将直线 AB 的解析式代入 中,得关于x的一元二次方程,得方程的解再设AB的垂直平分线上的任意一点Q(x,y),再由勾股定理进而即可求解.
解:(1)∵抛物线关于 y轴对称,∴b=0.
又∵抛物线过点(1, ),(2,1),
解得
∴抛物线的解析式为
(2)解法一:∵点 D(-1,p)在抛物线 上,
∵抛物线图象开口向上,且点 关于y轴的对称点的坐标为((1, ),
∴由图象可知,
当m-1=1或m-1=-1,即当m=2或m=0时,p=q;当m-1<-1或m-1>1,即当m<0或m>2时,p
∴当m=0或m=2时,p=q;当m<0或m>2时,p
解法二:
把 p-q看成关于m的函数,由图象可知,
当m=0或m=2时,p=q;
当m<0或m>2时,p
解法三:二次函数 开口向上,对称轴为y轴,
∴抛物线 上距离 y轴越远的点,函数值越大.
∵点 D到y 轴距离为1,
∴由图象可知,
当m-1=±1,即m=0或m=2时,p=q;
当m-1<-1或m-1>1,即m<0或m>2时,p
(3)解法一: 为定值,且定值是2.
设A(x ,y ),B(x ,y ),直线 AB的解析式为y= kx+1(k≠0).
把y= kx+1代入 中,得
则
如图,过点 B 作 BN⊥y轴,过点 A 作 AN∥y轴,交点为 N.
线段 AB中点 P 的坐标为(2k,2k +1).
又∵F(0,1),根据勾股定理,可得
∵∠MPF=∠BNA=90°,∠MFP=∠BFO=∠BAN,
∴△FPM∽△ANB,
解法.二: 为定值,且定值是2.
设A(x ,y ),B(x ,y ),直线 AB的解析式为y= kx+1(k≠0).
把y= kx+1代.入 中,得
则
设AB的垂直平分线上的任意一点Q 的坐标为(x,y).
根据勾股定理,可得
整理得
令x=0,得 即M(0,2k +3),
根据勾股定理,可得
4. (1) ① ② (2) S =
(1)①由已知条件得∠ADE=∠ACD,从而判断出∠ADE不发生变化并求得 sin∠ADE;②当 AE⊥DE时, 即可求解;(2)当0≤t≤1时, 当1
∴∠ADE的大小不会发生变化,
②线段 AE的最小值为
(2)由题意知PD=4t,PC=8-4t,当点 E刚好落在AC上时,P为CD 的中点,如图1,
∴4t=4,∴t=1.
当0≤t≤1时, 当1
由折叠知∠1=∠2.
∵PQ∥AC,∴∠1=∠4,∠2=∠3,
∴∠3=∠4,∴PC=PM=8-4t,∴EM=8t-8.
同理(QN=QA=6-3t,EN=6t-6,
(3)如图3,由题意知PD=PE=4t,PC=PF=8-4t,∴EF=FG=GA=8-8t,∴PG=16-12t.
过点G作GH⊥CD于点 H,
则DH=8-8t,PH=12t-8,
∴在 Rt△GPH中, 解得
5.(1)CD=2EF,理由略 (2)成立,证明略(3)
(1)利用直角三角形斜边中线的性质证明即可;(2)延长AC交BD 的延长线于点G,连接GM,GE,利用矩形的性质,直角三角形斜边中线的性质求解即可;(3)根据CD=2EF,CD=MG≥EG求解 EF 的最小值.
解:(1)CD=2EF.
理由如下:
∵△AMC 和△BMD都是等腰直角三角形,
∴∠ACM=∠MDB=90°,AC=MC,MD=BD,
∴∠CMD=180°-∠AMC-∠DMB=90°.
∵F是CD 的中点,
即CD=2MF.
∵点 M 与点 E 重合,
∴MF=EF,∴CD=2EF.
(2)成立.
证明:如图,延长 AC 交 BD 的延长线于点 G,连接GM,GE.
∵△AMC 和△BMD都是等腰直角三角形,
∴∠ACM=∠MDB=90°,AC=MC,MD=BD,
∴∠MCG=∠AGB=∠GDM=90°,AG=BG,
∴四边形 MCGD是矩形,△AGB是等腰直角三角形,
∴GM=CD.
∵E是AB 的中点,∴GE⊥AB,
∵F是CD 的中点,∴F 是GM 的中点.
在 Rt△MEG中,F是GM 的中点,
即CD=2EF.
(3)
6.(1)略 (2)
(1)由等边对等角得. ,由 B'C'∥BC得. ,再利用等腰
三角形两底角相等和折叠的性质得到∠BMP=∠CMQ,通过三角函数的定义可证得BP=CQ;(2)延长 PM与DC,延长线交于点E,作QF⊥ME于点F,由折叠及对顶角相等可得∠QME=45°,在 Rt△CMQ中,利用勾股定理求出MQ的长,设 BP=x,易证得△CME≌△BMP,表示出QE,QF,ME 的长,再利用等面积法列方程解出x的值,即可得到 BP 的长度;(3)延长 QM 交AB 的延长线于点H,作 PN⊥MH 于点 N.由折叠及对顶角相等可得∠PMH=60°,在 Rt△CMQ 中,利用勾股定理求出 MQ的长,设 BP=x,易证得△CMQ≌△BMH,表示出 PN,MH,PH的长,再利用等面积法列方程解出x的值,即可得到 BP的值.
解:(1)证明:∵M为BC的中点,∴MB=MC.
由折叠知B'M=BM,C'M=CM,
∵B'C'∥BC,
由折叠可知,
∴∠BMP=∠CMQ.
∵四边形ABCD是矩形,∴∠B=∠C=90°.
在 Rt△BMP 和 Rt△CMQ中可得,
∵MB=MC,∠BMP=∠CMQ,∴BP=CQ.
(2)如图所示,延长 PM与DC,延长线交于点 E,作 QF⊥ME于点 F.
∵MB'⊥MC',
再由折叠及对顶角相等可得∠QME=45°.
∵BC=6,M是BC 的中点,
∴BM=CM=3.
在 Rt△CMQ中,由勾股定理得
设BP=x,在 Rt△BPM中,由勾股定理得
在△CME 和△BMP中,
∵∠CME=∠BMP,CM=BM,
∠MCE=∠MBP=90°,
∴△CME≌△BMP,
在 Rt△MFQ中,∵∠QME=45°,MQ=
由 可得MC ·QE =FQ ·ME ,
解得 (不符合题意,舍去),
∴BP的长为
延长 QM 交 AB 的延长线于点 H,作 PN⊥MH 于点 N.
∵△C'MB'是等边三角形,
再由折叠及对顶角相等可得∠PMH=60°.
∵BC=6,M是BC 的中点,
∴BM=CM=3.
在 Rt△CMQ中,由勾股定理可得
设BP=x,在Rt△BPM中,由勾股定理得
在△CMQ 和△BMH中,
∵∠CMQ=∠BMH,CM=BM,∠MCQ=∠MBH=90°,
∴△CMQ≌△BMH,
在 Rt△PMN中,∵∠PMN=60°,PM=√x +9,
由 可得 PH ·
BM =HM ·PN ,
解得 不符合题意,舍去),
∴BP的长为
7.(1)C'(0,-4) y=-x+4 (2)(1,--1)(3)4
(1)对于抛物线解析式,令y=0,求得x的值,即可得点 B坐标,令x=0,可得到点C的坐标,利用待定系数法求得直线 BC 的解析式;(2)取 BC'的中点G,连接OG 交抛物线的对称轴于点M,过点 M 作 MH⊥y轴于点 H,根据已知条件证得OH=MH,由对称轴 得到 HM的长,从而得到点 M 的坐标;(3)过点 B 作 BI⊥PQ 于点Ⅰ,由已知条件得四边形 EOBI是矩形,证得 BI=OE,从而得到. ,根据点 P 在抛物线上,点Q 在直线 BC 上,得到点 P,Q的坐标,从而得到线段 PQ关于m 的二次函数的顶点式,即可求解.
解:(1)∵抛物线与x轴相交于点A,B,
当y=0时,
解得
∴B(4,0).
∵抛物线与 y轴相交于点C,
当x=0时,y=4,
∴C(0,4),∴C'(0,-4).
设 BC的表达式为y= kx+b,
将 B,C两点坐标分别代入得
解得
∴直线 BC的表达式为y=-x+4.
(2)取 BC'的中点G,连接OG 交抛物线的对称轴于点M,此时四边形 BMC'N 是以 BC'为对角线的菱形,过点 M作MH⊥y轴于点 H.
∴∠OMH=45°,
∴∠C'OG=∠OMH,
∴OH=MH.
∵抛物线的对称轴为直线
∴OH=MH=1,
∴M(1,-1).
(3)过点 B作BI⊥PQ于点I.
∵PQ∥x轴,∴∠IEO=90°.
∵∠IEO=∠EOB=∠BIE=90°,
∴四边形 EOBI是矩形,∴BI=OE,
=2QP.
∵点 P 在抛物线上,且点 P 的横坐标为m,
∴点 P 的纵坐标为
∵PQ∥x轴,
∴点 Q的纵坐标为 将其代入y=-x+4中,得点 Q的横坐标为
∵P是抛物线第一象限内一动点,
∴点 P 在点Q 右侧,
∴当m=2时,PQ的最大值是2.
的最大值是4.
同课章节目录
