类型7 实践操作题专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 类型7 实践操作题专项练习(含解析)--2025年中考数学一轮复习 |  | |
| 格式 | docx | ||
| 文件大小 | 546.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 19:04:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
类型7 实践操作题
1.实践操作型问题是指通过动手测量、作图(象)、取值、计算等实验,猜想获得数学结论的探索研究性活动,这类活动完全模拟以动手为基础的手脑结合的科学研究形式,需要动手操作、合情猜想和验证,不但有助于实践能力和创新能力的培养,更有助于养成实验研究的习惯,符合新课程标准特别强调的发现式学习、探究式学习和研究式学习,鼓励考生进行“微科研”活动,提倡要积极引导考生从事实验活动和实践活动,培养考生乐于动手、勤于实践的意识和习惯,切实提高考生的动手能力、实践能力的指导思想.因此,实践操作问题将成为今后中考的热点题型.
2.实践操作型的一种常见题型就是动手问题,此类题目考查考生动手操作能力,它包括裁剪、折叠、拼图,它既考查考生的动手能力,又考查考生的想象能力,往往与面积、对称的性质联系在一起.
3.动手操作的证明问题,既体现此类题型的动手能力,又能利用几何图形的性质进行全等、相似等证明.
4.操作探索型问题,这类在操作中进行探索的问题,要求我们以实际操作为问题背景去探索操作背后所包含的数学内容.这类问题的解题策略是在操作中发挥合理的想象,结合实际去观察操作中的图形位置的变化、数量关系的变化并根据这些变化进行观察、试验、类比、归纳、猜想活动.在这类问题的探索中,我们要注意把实际的操作问题转化为相对应的数学问题并积极运用操作过程中所蕴涵的数学知识去解决问题,操作探索型问题是解题策略开放题,现在更多的是以要求解题者设计解题方案来设计题目.
【例1】如图,在△ABC中,按以下步骤作图:
①分别以点 A,B 为圆心,大于 AB 的长为半径画弧,两弧交于 P,Q两点;
②作直线 PQ交AB 于点 D;
③以点 D 为圆心,AD 长为半径画弧交PQ 于点M,连接AM,BM.
若 ,则AM的长为 ( )
A.4 B.2 C. D.
【解析】本题考查尺规作图、特殊角的三角函数.由作图可知 PQ是线段AB 的垂直平分线,所以 AM=BM,由 DA=DB=DM可知∠AMB=90°,所以△AMB是等腰直角三角形,所以∠ABM=45°,所以 AM=AB· 故选 B.
【答案】B
【例2】在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 60°,30°,15°等大小的角,可以采用如下方法:
操作感知:
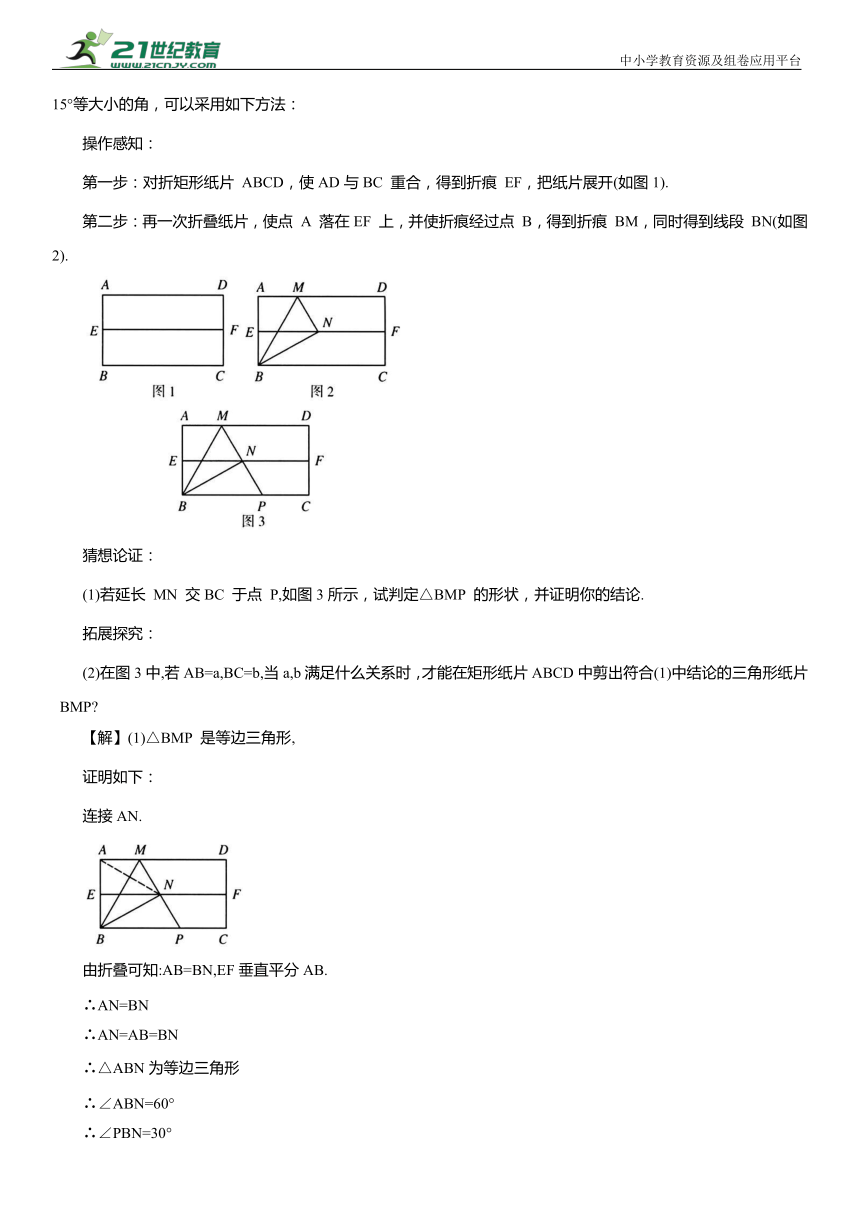
第一步:对折矩形纸片 ABCD,使AD与BC 重合,得到折痕 EF,把纸片展开(如图1).
第二步:再一次折叠纸片,使点 A 落在EF 上,并使折痕经过点 B,得到折痕 BM,同时得到线段 BN(如图2).
猜想论证:
(1)若延长 MN 交BC 于点 P,如图3所示,试判定△BMP 的形状,并证明你的结论.
拓展探究:
(2)在图3中,若AB=a,BC=b,当a,b满足什么关系时,才能在矩形纸片ABCD中剪出符合(1)中结论的三角形纸片 BMP
【解】(1)△BMP 是等边三角形,
证明如下:
连接AN.
由折叠可知:AB=BN,EF垂直平分AB.
∴AN=BN
∴AN=AB=BN
∴△ABN为等边三角形
∴∠ABN=60°
∴∠PBN=30°
∵∠ABM=∠NBM=30°,∠BNM=∠BAM=90°
∴∠BMP=60°,
∴∠MBP=∠BMP=∠BPM=60°
∴△BMP 是等边三角形.
(2)方法一:要在矩形纸片 ABCD 上剪出等边△BMP,则 BC≥BP
在 Rt△BNP中,BN=BA=a,
∵BC≥BP
即
当 或 时,在矩形纸片上能剪出这样的等边△BMP.
方法二:(仅供参考,酌情给分)
要 在 矩 形 纸 片 ABCD 上 剪 出 等边△BMP,
则 BC≥BP在 Rt△BNP 中,∠NBP=30°,BN=AB=a,
设 NP=x,则 BP=2x
即 得
∵BC≥BP
即
当 或 时,在矩形纸片上能剪出这样的等边△BMP.
1.如图,在△ABC 中,分别以点 B 和点 C 为圆心,大于 BC长为半径画弧,两弧相交于点 M,N.作直线 MN,交 AC 于点D,交 BC 于点E,连接 BD.若AB=7,AC=12,BC=6,则△ABD 的周长为 ( )
A.25 B.22
C.19 D.18
2.如图,在△ABC 中,AB=AC,以点 B 为圆心,适当长为半径画弧,交BA 于点M,交 BC 于点 N,分别以点 M、N为圆心,大于 MN 的长为半径画弧,两弧在∠ABC的内部相交于点 P,画射线BP,交AC于点D,若AD=BD,则∠A的度数是( )
A.36° B.54°
C.72° D.108°
3.如图,在矩形 ABCD中,AB下列结论:
①四边形AECF是菱形;
②∠AFB=2∠ACB;
③AC·EF=CF·CD;
④若AF平分∠BAC,则CF=2BF.
其中正确结论的个数是 ( )
A.4 B.3
C.2 D.1
4.如图,等腰△AOB 中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点 P(不与点 A,B 重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP 的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接 M,E,N,F 四点必能得到矩形;
结论Ⅱ:⊙O 上只有唯一的点 P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D. Ⅰ对Ⅱ不对
5.如图,在△ABC中,按以下步骤作图:①分别以点 B 和C 为圆心,以大于 BC 的长为半径作弧,两弧相交于点 M 和 N;②作直线MN交 AC 于点 D,连接 BD.若 AC=6,AD=2,则 BD的长为 ( )
A.2 B.3
C.4 D.6
6.如图,在△ABC中,按以下步骤作图:①分别以点 B 和 C 为圆心,以大于 BC的长为半径作弧,两弧相交于点M和N;②作直线 MN 交边 AB 于点E.若AC=5,BE=4,∠B=45°,则 AB 的长为 .
7.如图,在平行四边形ABCD中,AB⊥AC,AB=3,AC=4,分别以A,C为圆心,大于 AC 的长为半径画弧,两弧相交于点 M,N,过M,N两点作直线,与 BC交于点 E,与 AD 交于点 F,连接AE, CF. 则 四 边 形 AECF 的 周 长为 .
8.如图,在△ABC 中,∠BAC>90°,分别以点 A,B为圆心,以大于 AB长为半径画弧,两弧交于点 D,E.作直线 DE,交 BC于点 M.分别以点 A,C为圆心,以大于 AC长为半径画弧,两弧交于点 F,G.作直线 FG,交 BC于点N.连接 AM, AN. 若 ∠BAC = α, 则∠MAN= .
9.如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积
如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
如图 2,已知线段 MN,请你用圆规和无刻度的直尺作一个以 MN 为斜边的等腰直角三角形MNP;
如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点 O 为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)
10.如图,BD 是矩形ABCD 的对角线.
(1)求作⊙A,使得⊙A 与 BD 相切(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,设 BD与⊙A 相切于点E,CF⊥BD,垂足为 F.若直线 CF 与⊙A 相切于点G,求 tan∠ADB 的值.
11.能够完全重合的平行四边形纸片 ABCD 和AEFG 按图 1方式摆放,其中AD=AG=5,AB=9.点 D,G分别在边AE,AB上,CD与FG 相交于点 H.
求证:四边形 AGHD 是菱形;
固定图1中的平行四边形纸片ABCD,将平行四边形纸片 AEFG 绕着点A 顺时针旋转一定的角度,使点 F 与点C重合,如图2.则这两张平行四边形纸片未重叠部分图形的周长和为 ;
将图 2 中的平行四边形纸片AEFG 绕着点 A 继续顺时针旋转一定的角度,使点 E 与点 B 重合,连接 DG,CF,如图 3. 若 则四边形DCFG的面积为 .
压轴预测
1.如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下:
下列判断正确的是 ( )
A.甲、乙能得到a∥b,丙不能
B.甲、丙能得到a∥b,乙不能
C.乙、丙能得到a∥b,甲不能
D.甲、乙、丙均能得到a∥b
2.如图,直线 MN∥PQ,直线 AB 分别与MN,PQ 相交于点A,B.小宇同学利用以下步骤作图:
①以点 A 为圆心,适当长为半径作弧交射线 AN于点C,交线段AB于点D;
②以点 C 为圆心,适当长为半径画弧,然后再以点 D 为圆心,同样长为半径画弧.前后两弧在∠NAB 内交于点E;
③作射线 AE,交 PQ于点 F.
若AF=2 ,∠FAN=30°,则线段 BF 的长为 .
3.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在 AB边上求作点D,使 DB=DC;
(2)在 AC 边上求作点 E,使△ADE∽△ACB.
4.在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,已知⊙O经过点C,且与 AB 相切于点D.
(1)在图1 中作出⊙O;(要求:尺规作图,不写作法,保留作图痕迹)
(2)若点 D 是边 AB 上的动点,设⊙O 与边CA,CB 分别相交于点 E,F,求 EF 的最小值.
5.动手操作:
第一步:如图1,将正方形纸片 ABCD 折叠,使AB 与 CD 重合,展开铺平,折痕为EF;
第二步:将正方形纸片 ABCD 沿直线 BM折叠,使点 A 落在 EF 上的点 G 处,得折痕为 BM,展开铺平,如图 2,延长 MG 交CD 于点 P.
解决问题:
(1)判断 PG 与 PC 的数量关系,并说明理由;
(2)①求∠DMP 的度数;
②求 的值;
(3)如图3,若将正方形 ABCD 改为矩形ABCD,且 其余操作不变,请直接写出 的值.
类型7 实践操作题
1. C 【解析】本题考查尺规作图、垂直平分线的性质.由尺规作图可知,MN 是线段BC 的垂直平分线,所以 BD=CD,所以△ABD的周长为AB+BD+AD=AB+CD+AD=AB+AC=7+12=19,故选C.
2. A 【解析】本题考查尺规作图、三角形内角和定理、等腰三角形的性质.根据作图可得∠ABD=∠CBD.设∠A=x,∵AD=BD,∴∠ABD=∠CBD=∠A=x.∵AB=AC,∴∠ABC=∠C=2x.在△ABC 中,∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°,∴x=36°,故选 A.
3. B 【解析】本题考查矩形的性质、尺规作图、菱形的判定与面积公式.如图,设 AC,EF交于点O.在矩形 ABCD中,AD∥BC,所以∠EAO=∠FCO,∠AEO=∠CFO.由尺规作图可知,EF垂直平分线段AC,所以OA=OC,所以△AOE≌△COF(AAS),所以OE=OF,即 EF 与AC互相垂直平分,所以四边形 AECF 是菱形,故①正确;易知 AF = FC,所以∠FAO=∠ACB,所以∠AFB =∠FAO+∠ACB=2∠ACB,故②正确;因为 S菱形AECF= 所以 AC·EF=2CF·CD,故③错误;若 AF 平分∠BAC,则∠BAF=∠FAC= 所以AF=2BF.因为CF=AF,所以CF=2BF,故④正确.综上,正确结论的个数是3,故选 B.
4. D 【解析】本题考查尺规作图、线段的垂直平分线的性质、矩形的判定、扇形的面积公式,连接 EM,EN,MF,NF.∵OM=ON,OE=OF,∴四边形 MENF 是平行四边形.∵EF=MN,∴四边形 MENF 是矩形,故Ⅰ正确;由图知当∠MOF=∠AOB时,S扇形FOM =S扇形AOB,由于圆 的对称性,这样的点 P 在直线 MN 的右侧仍有一个,∴这样的点 P 不唯一,故Ⅱ错误,故选 D.
5. C 【解析】本题考查线段垂直平分线的性质.由作图可知,MN是线段 BC 的垂直平分线,∴DB=DC.∵AC=6,AD=2,∴DC=AC-AD=4,∴BD=4,即 BD的长为4,故选 C.
6.7 【解析】本题考查线段垂直平分线的性质、勾股定理.如图,连接EC,由作图可知,直线 MN 是线段 BC的垂直平 分 线, ∴ EB = EC = 4, ∴ ∠B = ∠ECB= 45°,∴∠BEC=90°.在 Rt△ACE中,AC=5,由勾股定理可得AE=3,∴AB=AE+BE=7,即AB的长为7.
7.10 【解析】本题考查尺规作图、线段垂直平分线的性质、平行四边形的性质、等腰三角形的性质、菱形的判定与性质.由作图可知,MN 是线段 AC 的垂直平分线,∴AE=EC,AF = FC,∴∠EAC =∠ECA,∠FAC =∠FCA.在平行四边形 ABCD中,AD∥BC,∴∠FAC=∠ACE,∴∠FAC=∠CAE,∴AE=AF,∴AE=EC=CF=AF,∴四边形AECF 是菱形,∴EF⊥AC.设菱形的对角线 AC,EF 交于点O,则 O 是 AC,EF 的中点.∵AB⊥AC,∴EF∥AB,∴E是 BC 的中点.在 Rt△ABC中,AB=3,AC=4,∴BC=5,∴EC= BC= , ∴菱形AECF 的周长为
8.2α-180° 【解析】本题考查尺规作图、线段垂直平分线的判定和性质.由作图知DE垂直平分线段AB,FG垂直平分线段 AC,∴∠B =∠BAM,∠C = ∠NAC.
∵∠B+∠C+∠BAC=180°,∴∠B+∠C+∠BAC+∠MAN= ∠BAM +∠NAC + ∠MAN + ∠BAC=180°+ ∠MAN, ∴2∠BAC= 180° + ∠MAN,∴∠MAN=2α-180°.
9.略
作 AB 的垂直平分线或作∠AOB 的平分线即可;【问题联想】作 MN 的垂直平分线,再以 MN 为直径作圆,交垂直平分线于点 P,即可作出等腰直角三角形MNP;【问题再解】以半径为斜边作等腰直角三角形,再以其直角边长为半径作弧即可.
解:如图 1 所示.
如图2 所示.
如图3所示.
10.(1)略
(1)过点 A 作BD 的垂线,以点 A 为圆心,垂线段长为半径作⊙A,⊙A 即为所求;(2)由切线的性质及矩形的判定证明四边形 AEFG为矩形,再证明四边形 AEFG为正方形,利用同角的余角相等得∠BAE=∠ADB,结合正切函数的概念表示出 BE,由矩形的性质和全等三角形的判定证明△ABE≌△CDF,得对应边相等,从而表示出 DE,再根据正切函数的概念建立一元二次方程,解方程即可求得 tan∠ADB的值.
解:(1)如图所示,⊙A 即为所求作.
(2)设∠ADB=α,⊙A 的半径为r.
∵BD与⊙A 相切于点E,CF与⊙A 相切于点G,
∴AE⊥BD,AG⊥CG,
即∠AEF=∠AGF=90°.
∵CF⊥BD,
∴∠EFG=90°,
∴四边形 AEFG 是矩形.
又AE=AG=r,
∴四边形 AEFG是正方形.
∴EF=AE=r.
在 Rt△AEB 和 Rt△DAB中,
∠BAE+∠ABD=90°,∠ADB+∠ABD=90°,
∴∠BAE=∠ADB=α.
在 Rt△ABE中,
∴BE=rtanα.
∵四边形ABCD 是矩形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
又∠AEB=∠CFD=90°,
∴△ABE≌△CDF,
∴BE=DF=rtanα,
∴DE=DF+EF=rtanα+r.
在 Rt△ADE中,
即 DE·tanα=AE,
∴(rtanα+r)tanα=r,
即
∵tanα>0,
即 tan∠ADB的值为
11.略 【操作一】56 【操作二】72
【探究】根据两组对边分别平行证明四边形 AGHD 是平行四边形,再结合一组邻边相等,可证四边形AGHD是菱形;【操作一】由图可知,旋转后未重叠部分的周长等于原平行四边形的周长的2倍,即可求解;【操作二】由平行四边形的性质和旋转图形的性质可证 AB⊥DG,在直角三角形中利用已知的锐角三角函数求出DG的长.又可证四边形 DCFG是矩形,即可求出它的面积.
解:【探究】
证明:∵四边形 ABCD 和AEFG 是平行四边形,
∴AE∥FG,AB∥DC,
∴AD∥GH,AG∥DH,
∴四边形 AGHD是平行四边形.
∵AD=AG,
∴四边形 AGHD是菱形.
压轴预测
1. B 【解析】本题考查全等三角形的判定与性质、平行线的判定.甲:∵∠1=∠2,∴a∥b(内错角相等,两直线平行);乙:由∠1=∠2,不能判定a∥b;丙:在△AOC 和△BOD中, () ∴∠CAO=∠DBO,∴a∥b,∴甲、丙能得到a∥b,乙不能,故选 B.
2.2 【解析】本题考查尺规作图、平行线的性质、特殊角的三角函数值.如图,过点 B 作 BG⊥AF 于点 G.因为MN∥PQ,所以∠2 =∠3 = 30°. 由题意得 AF 平分∠NAB,所以 ,所以∠1=∠3=30°,所以AB=BF.又BG⊥AF,所以 所以在Rt△BFG中,
3.(1)略 (2)略
(1)作线段 BC的垂直平分线交 AB 于点 D,连接CD,点 D 即为所求;(2)作∠ADT=∠ACB,射线 DT 交AC于点E,点E 即为所求.
解:(1)如图,点D 即为所求.
(2)如图,点E 即为所求.
4.(1)略 (2)4.8
(1)连接CD,作线段CD的垂直平分线交过点 D 垂直于AB 的直线于点O,以O为圆心,OD 长为半径作出⊙O即可;(2)连接CO,OD,过点C作CT⊥AB于点T,利用三角形等面积法求出CT,再根据垂线段最短即可得出结论.
解:(1)如图,⊙O是所求作的圆.
(2)如图所示,连接CO,OD,过点C作CT⊥AB于点 T.
在Rt△ABC中,AC=6,BC=8,
由勾股定理得
解得CT=4.8.
∵∠ACB=90°,
∴EF 是⊙O的直径.
∵EF=CO+OD≥CD≥CT,
∴当C,O,D三点共线时,点D 与点 T 重合,如图所示,
此时EF 的最小值为(CT=4.8.
5.(1)PG=PC,理由略 (2)①30°
(3)
(1)连接BP,由折叠的性质可得出∠MGB=∠A=90°,BG=AB,利用“HL”证明 Rt△BGP≌Rt△BCP,由全等三角形的性质即可得解;(2)①连接CG,证明△BCG为等边三角形,由等边三角形的性质得出∠GBF=60°,进而求得∠BGF=30°,根据平角的定义求出∠MGE 的度数,即可求解;②设出 EG的长度,分别表示出 AM,ME,DE的长度,证明△MEG∽△MDP,由相似三角形的性质即可求解;(3)设 AB=5a,BC=6a,证明△MEG∽△GFB,求出 ME,MD的长,再证明△MEG∽△MDP,由相似三角形的性质即可求解.
解:(1)PG=PC.理由如下:连接 BP,如图1.
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC.
将正方形纸片ABCD沿直线BM 折叠,
∴∠MGB=∠A=90°,BG=AB,
∴BG=BC.
在 Rt△BGP 和 Rt△BCP 中
∴Rt△BGP≌Rt△BCP(HL),
∴PG=PC.
(2)①连接CG,如图2.
∵EF为折痕,
∴FG是BC 的垂直平分线,
∴BG=CG,
由(1)知BG=BC,
∴BG=CG=BC,
∴△BCG为等边三角形,
∴∠GBF=60°.∴∠BGF=30°.
∵∠BGM=90°.
∴∠MGE=60°.
②设EG=x.∵∠EMG=30°,
∴AM=MG=2x,
∵EG∥DP,∴△MEG∽△MDP,
(3) .【解题过程】:
设AB=5a,BC=6a,
∴BF=CF=3a.
∵△ABM沿直线BM 折叠,
∴∠BGM=∠A=90°,BG=AB=5a,
∴EG=a.
∵∠MGE+∠BGF=90°,∠BGF+∠GBF=90°,
∴∠MGE=∠GBF,
∴△MEG∽△GFB,
∵EG∥DP,∴△MEG∽△MDP,
类型7 实践操作题
1.实践操作型问题是指通过动手测量、作图(象)、取值、计算等实验,猜想获得数学结论的探索研究性活动,这类活动完全模拟以动手为基础的手脑结合的科学研究形式,需要动手操作、合情猜想和验证,不但有助于实践能力和创新能力的培养,更有助于养成实验研究的习惯,符合新课程标准特别强调的发现式学习、探究式学习和研究式学习,鼓励考生进行“微科研”活动,提倡要积极引导考生从事实验活动和实践活动,培养考生乐于动手、勤于实践的意识和习惯,切实提高考生的动手能力、实践能力的指导思想.因此,实践操作问题将成为今后中考的热点题型.
2.实践操作型的一种常见题型就是动手问题,此类题目考查考生动手操作能力,它包括裁剪、折叠、拼图,它既考查考生的动手能力,又考查考生的想象能力,往往与面积、对称的性质联系在一起.
3.动手操作的证明问题,既体现此类题型的动手能力,又能利用几何图形的性质进行全等、相似等证明.
4.操作探索型问题,这类在操作中进行探索的问题,要求我们以实际操作为问题背景去探索操作背后所包含的数学内容.这类问题的解题策略是在操作中发挥合理的想象,结合实际去观察操作中的图形位置的变化、数量关系的变化并根据这些变化进行观察、试验、类比、归纳、猜想活动.在这类问题的探索中,我们要注意把实际的操作问题转化为相对应的数学问题并积极运用操作过程中所蕴涵的数学知识去解决问题,操作探索型问题是解题策略开放题,现在更多的是以要求解题者设计解题方案来设计题目.
【例1】如图,在△ABC中,按以下步骤作图:
①分别以点 A,B 为圆心,大于 AB 的长为半径画弧,两弧交于 P,Q两点;
②作直线 PQ交AB 于点 D;
③以点 D 为圆心,AD 长为半径画弧交PQ 于点M,连接AM,BM.
若 ,则AM的长为 ( )
A.4 B.2 C. D.
【解析】本题考查尺规作图、特殊角的三角函数.由作图可知 PQ是线段AB 的垂直平分线,所以 AM=BM,由 DA=DB=DM可知∠AMB=90°,所以△AMB是等腰直角三角形,所以∠ABM=45°,所以 AM=AB· 故选 B.
【答案】B
【例2】在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 60°,30°,15°等大小的角,可以采用如下方法:
操作感知:
第一步:对折矩形纸片 ABCD,使AD与BC 重合,得到折痕 EF,把纸片展开(如图1).
第二步:再一次折叠纸片,使点 A 落在EF 上,并使折痕经过点 B,得到折痕 BM,同时得到线段 BN(如图2).
猜想论证:
(1)若延长 MN 交BC 于点 P,如图3所示,试判定△BMP 的形状,并证明你的结论.
拓展探究:
(2)在图3中,若AB=a,BC=b,当a,b满足什么关系时,才能在矩形纸片ABCD中剪出符合(1)中结论的三角形纸片 BMP
【解】(1)△BMP 是等边三角形,
证明如下:
连接AN.
由折叠可知:AB=BN,EF垂直平分AB.
∴AN=BN
∴AN=AB=BN
∴△ABN为等边三角形
∴∠ABN=60°
∴∠PBN=30°
∵∠ABM=∠NBM=30°,∠BNM=∠BAM=90°
∴∠BMP=60°,
∴∠MBP=∠BMP=∠BPM=60°
∴△BMP 是等边三角形.
(2)方法一:要在矩形纸片 ABCD 上剪出等边△BMP,则 BC≥BP
在 Rt△BNP中,BN=BA=a,
∵BC≥BP
即
当 或 时,在矩形纸片上能剪出这样的等边△BMP.
方法二:(仅供参考,酌情给分)
要 在 矩 形 纸 片 ABCD 上 剪 出 等边△BMP,
则 BC≥BP在 Rt△BNP 中,∠NBP=30°,BN=AB=a,
设 NP=x,则 BP=2x
即 得
∵BC≥BP
即
当 或 时,在矩形纸片上能剪出这样的等边△BMP.
1.如图,在△ABC 中,分别以点 B 和点 C 为圆心,大于 BC长为半径画弧,两弧相交于点 M,N.作直线 MN,交 AC 于点D,交 BC 于点E,连接 BD.若AB=7,AC=12,BC=6,则△ABD 的周长为 ( )
A.25 B.22
C.19 D.18
2.如图,在△ABC 中,AB=AC,以点 B 为圆心,适当长为半径画弧,交BA 于点M,交 BC 于点 N,分别以点 M、N为圆心,大于 MN 的长为半径画弧,两弧在∠ABC的内部相交于点 P,画射线BP,交AC于点D,若AD=BD,则∠A的度数是( )
A.36° B.54°
C.72° D.108°
3.如图,在矩形 ABCD中,AB
①四边形AECF是菱形;
②∠AFB=2∠ACB;
③AC·EF=CF·CD;
④若AF平分∠BAC,则CF=2BF.
其中正确结论的个数是 ( )
A.4 B.3
C.2 D.1
4.如图,等腰△AOB 中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点 P(不与点 A,B 重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP 的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接 M,E,N,F 四点必能得到矩形;
结论Ⅱ:⊙O 上只有唯一的点 P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D. Ⅰ对Ⅱ不对
5.如图,在△ABC中,按以下步骤作图:①分别以点 B 和C 为圆心,以大于 BC 的长为半径作弧,两弧相交于点 M 和 N;②作直线MN交 AC 于点 D,连接 BD.若 AC=6,AD=2,则 BD的长为 ( )
A.2 B.3
C.4 D.6
6.如图,在△ABC中,按以下步骤作图:①分别以点 B 和 C 为圆心,以大于 BC的长为半径作弧,两弧相交于点M和N;②作直线 MN 交边 AB 于点E.若AC=5,BE=4,∠B=45°,则 AB 的长为 .
7.如图,在平行四边形ABCD中,AB⊥AC,AB=3,AC=4,分别以A,C为圆心,大于 AC 的长为半径画弧,两弧相交于点 M,N,过M,N两点作直线,与 BC交于点 E,与 AD 交于点 F,连接AE, CF. 则 四 边 形 AECF 的 周 长为 .
8.如图,在△ABC 中,∠BAC>90°,分别以点 A,B为圆心,以大于 AB长为半径画弧,两弧交于点 D,E.作直线 DE,交 BC于点 M.分别以点 A,C为圆心,以大于 AC长为半径画弧,两弧交于点 F,G.作直线 FG,交 BC于点N.连接 AM, AN. 若 ∠BAC = α, 则∠MAN= .
9.如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积
如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
如图 2,已知线段 MN,请你用圆规和无刻度的直尺作一个以 MN 为斜边的等腰直角三角形MNP;
如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点 O 为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)
10.如图,BD 是矩形ABCD 的对角线.
(1)求作⊙A,使得⊙A 与 BD 相切(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,设 BD与⊙A 相切于点E,CF⊥BD,垂足为 F.若直线 CF 与⊙A 相切于点G,求 tan∠ADB 的值.
11.能够完全重合的平行四边形纸片 ABCD 和AEFG 按图 1方式摆放,其中AD=AG=5,AB=9.点 D,G分别在边AE,AB上,CD与FG 相交于点 H.
求证:四边形 AGHD 是菱形;
固定图1中的平行四边形纸片ABCD,将平行四边形纸片 AEFG 绕着点A 顺时针旋转一定的角度,使点 F 与点C重合,如图2.则这两张平行四边形纸片未重叠部分图形的周长和为 ;
将图 2 中的平行四边形纸片AEFG 绕着点 A 继续顺时针旋转一定的角度,使点 E 与点 B 重合,连接 DG,CF,如图 3. 若 则四边形DCFG的面积为 .
压轴预测
1.如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下:
下列判断正确的是 ( )
A.甲、乙能得到a∥b,丙不能
B.甲、丙能得到a∥b,乙不能
C.乙、丙能得到a∥b,甲不能
D.甲、乙、丙均能得到a∥b
2.如图,直线 MN∥PQ,直线 AB 分别与MN,PQ 相交于点A,B.小宇同学利用以下步骤作图:
①以点 A 为圆心,适当长为半径作弧交射线 AN于点C,交线段AB于点D;
②以点 C 为圆心,适当长为半径画弧,然后再以点 D 为圆心,同样长为半径画弧.前后两弧在∠NAB 内交于点E;
③作射线 AE,交 PQ于点 F.
若AF=2 ,∠FAN=30°,则线段 BF 的长为 .
3.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在 AB边上求作点D,使 DB=DC;
(2)在 AC 边上求作点 E,使△ADE∽△ACB.
4.在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,已知⊙O经过点C,且与 AB 相切于点D.
(1)在图1 中作出⊙O;(要求:尺规作图,不写作法,保留作图痕迹)
(2)若点 D 是边 AB 上的动点,设⊙O 与边CA,CB 分别相交于点 E,F,求 EF 的最小值.
5.动手操作:
第一步:如图1,将正方形纸片 ABCD 折叠,使AB 与 CD 重合,展开铺平,折痕为EF;
第二步:将正方形纸片 ABCD 沿直线 BM折叠,使点 A 落在 EF 上的点 G 处,得折痕为 BM,展开铺平,如图 2,延长 MG 交CD 于点 P.
解决问题:
(1)判断 PG 与 PC 的数量关系,并说明理由;
(2)①求∠DMP 的度数;
②求 的值;
(3)如图3,若将正方形 ABCD 改为矩形ABCD,且 其余操作不变,请直接写出 的值.
类型7 实践操作题
1. C 【解析】本题考查尺规作图、垂直平分线的性质.由尺规作图可知,MN 是线段BC 的垂直平分线,所以 BD=CD,所以△ABD的周长为AB+BD+AD=AB+CD+AD=AB+AC=7+12=19,故选C.
2. A 【解析】本题考查尺规作图、三角形内角和定理、等腰三角形的性质.根据作图可得∠ABD=∠CBD.设∠A=x,∵AD=BD,∴∠ABD=∠CBD=∠A=x.∵AB=AC,∴∠ABC=∠C=2x.在△ABC 中,∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°,∴x=36°,故选 A.
3. B 【解析】本题考查矩形的性质、尺规作图、菱形的判定与面积公式.如图,设 AC,EF交于点O.在矩形 ABCD中,AD∥BC,所以∠EAO=∠FCO,∠AEO=∠CFO.由尺规作图可知,EF垂直平分线段AC,所以OA=OC,所以△AOE≌△COF(AAS),所以OE=OF,即 EF 与AC互相垂直平分,所以四边形 AECF 是菱形,故①正确;易知 AF = FC,所以∠FAO=∠ACB,所以∠AFB =∠FAO+∠ACB=2∠ACB,故②正确;因为 S菱形AECF= 所以 AC·EF=2CF·CD,故③错误;若 AF 平分∠BAC,则∠BAF=∠FAC= 所以AF=2BF.因为CF=AF,所以CF=2BF,故④正确.综上,正确结论的个数是3,故选 B.
4. D 【解析】本题考查尺规作图、线段的垂直平分线的性质、矩形的判定、扇形的面积公式,连接 EM,EN,MF,NF.∵OM=ON,OE=OF,∴四边形 MENF 是平行四边形.∵EF=MN,∴四边形 MENF 是矩形,故Ⅰ正确;由图知当∠MOF=∠AOB时,S扇形FOM =S扇形AOB,由于圆 的对称性,这样的点 P 在直线 MN 的右侧仍有一个,∴这样的点 P 不唯一,故Ⅱ错误,故选 D.
5. C 【解析】本题考查线段垂直平分线的性质.由作图可知,MN是线段 BC 的垂直平分线,∴DB=DC.∵AC=6,AD=2,∴DC=AC-AD=4,∴BD=4,即 BD的长为4,故选 C.
6.7 【解析】本题考查线段垂直平分线的性质、勾股定理.如图,连接EC,由作图可知,直线 MN 是线段 BC的垂直平 分 线, ∴ EB = EC = 4, ∴ ∠B = ∠ECB= 45°,∴∠BEC=90°.在 Rt△ACE中,AC=5,由勾股定理可得AE=3,∴AB=AE+BE=7,即AB的长为7.
7.10 【解析】本题考查尺规作图、线段垂直平分线的性质、平行四边形的性质、等腰三角形的性质、菱形的判定与性质.由作图可知,MN 是线段 AC 的垂直平分线,∴AE=EC,AF = FC,∴∠EAC =∠ECA,∠FAC =∠FCA.在平行四边形 ABCD中,AD∥BC,∴∠FAC=∠ACE,∴∠FAC=∠CAE,∴AE=AF,∴AE=EC=CF=AF,∴四边形AECF 是菱形,∴EF⊥AC.设菱形的对角线 AC,EF 交于点O,则 O 是 AC,EF 的中点.∵AB⊥AC,∴EF∥AB,∴E是 BC 的中点.在 Rt△ABC中,AB=3,AC=4,∴BC=5,∴EC= BC= , ∴菱形AECF 的周长为
8.2α-180° 【解析】本题考查尺规作图、线段垂直平分线的判定和性质.由作图知DE垂直平分线段AB,FG垂直平分线段 AC,∴∠B =∠BAM,∠C = ∠NAC.
∵∠B+∠C+∠BAC=180°,∴∠B+∠C+∠BAC+∠MAN= ∠BAM +∠NAC + ∠MAN + ∠BAC=180°+ ∠MAN, ∴2∠BAC= 180° + ∠MAN,∴∠MAN=2α-180°.
9.略
作 AB 的垂直平分线或作∠AOB 的平分线即可;【问题联想】作 MN 的垂直平分线,再以 MN 为直径作圆,交垂直平分线于点 P,即可作出等腰直角三角形MNP;【问题再解】以半径为斜边作等腰直角三角形,再以其直角边长为半径作弧即可.
解:如图 1 所示.
如图2 所示.
如图3所示.
10.(1)略
(1)过点 A 作BD 的垂线,以点 A 为圆心,垂线段长为半径作⊙A,⊙A 即为所求;(2)由切线的性质及矩形的判定证明四边形 AEFG为矩形,再证明四边形 AEFG为正方形,利用同角的余角相等得∠BAE=∠ADB,结合正切函数的概念表示出 BE,由矩形的性质和全等三角形的判定证明△ABE≌△CDF,得对应边相等,从而表示出 DE,再根据正切函数的概念建立一元二次方程,解方程即可求得 tan∠ADB的值.
解:(1)如图所示,⊙A 即为所求作.
(2)设∠ADB=α,⊙A 的半径为r.
∵BD与⊙A 相切于点E,CF与⊙A 相切于点G,
∴AE⊥BD,AG⊥CG,
即∠AEF=∠AGF=90°.
∵CF⊥BD,
∴∠EFG=90°,
∴四边形 AEFG 是矩形.
又AE=AG=r,
∴四边形 AEFG是正方形.
∴EF=AE=r.
在 Rt△AEB 和 Rt△DAB中,
∠BAE+∠ABD=90°,∠ADB+∠ABD=90°,
∴∠BAE=∠ADB=α.
在 Rt△ABE中,
∴BE=rtanα.
∵四边形ABCD 是矩形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
又∠AEB=∠CFD=90°,
∴△ABE≌△CDF,
∴BE=DF=rtanα,
∴DE=DF+EF=rtanα+r.
在 Rt△ADE中,
即 DE·tanα=AE,
∴(rtanα+r)tanα=r,
即
∵tanα>0,
即 tan∠ADB的值为
11.略 【操作一】56 【操作二】72
【探究】根据两组对边分别平行证明四边形 AGHD 是平行四边形,再结合一组邻边相等,可证四边形AGHD是菱形;【操作一】由图可知,旋转后未重叠部分的周长等于原平行四边形的周长的2倍,即可求解;【操作二】由平行四边形的性质和旋转图形的性质可证 AB⊥DG,在直角三角形中利用已知的锐角三角函数求出DG的长.又可证四边形 DCFG是矩形,即可求出它的面积.
解:【探究】
证明:∵四边形 ABCD 和AEFG 是平行四边形,
∴AE∥FG,AB∥DC,
∴AD∥GH,AG∥DH,
∴四边形 AGHD是平行四边形.
∵AD=AG,
∴四边形 AGHD是菱形.
压轴预测
1. B 【解析】本题考查全等三角形的判定与性质、平行线的判定.甲:∵∠1=∠2,∴a∥b(内错角相等,两直线平行);乙:由∠1=∠2,不能判定a∥b;丙:在△AOC 和△BOD中, () ∴∠CAO=∠DBO,∴a∥b,∴甲、丙能得到a∥b,乙不能,故选 B.
2.2 【解析】本题考查尺规作图、平行线的性质、特殊角的三角函数值.如图,过点 B 作 BG⊥AF 于点 G.因为MN∥PQ,所以∠2 =∠3 = 30°. 由题意得 AF 平分∠NAB,所以 ,所以∠1=∠3=30°,所以AB=BF.又BG⊥AF,所以 所以在Rt△BFG中,
3.(1)略 (2)略
(1)作线段 BC的垂直平分线交 AB 于点 D,连接CD,点 D 即为所求;(2)作∠ADT=∠ACB,射线 DT 交AC于点E,点E 即为所求.
解:(1)如图,点D 即为所求.
(2)如图,点E 即为所求.
4.(1)略 (2)4.8
(1)连接CD,作线段CD的垂直平分线交过点 D 垂直于AB 的直线于点O,以O为圆心,OD 长为半径作出⊙O即可;(2)连接CO,OD,过点C作CT⊥AB于点T,利用三角形等面积法求出CT,再根据垂线段最短即可得出结论.
解:(1)如图,⊙O是所求作的圆.
(2)如图所示,连接CO,OD,过点C作CT⊥AB于点 T.
在Rt△ABC中,AC=6,BC=8,
由勾股定理得
解得CT=4.8.
∵∠ACB=90°,
∴EF 是⊙O的直径.
∵EF=CO+OD≥CD≥CT,
∴当C,O,D三点共线时,点D 与点 T 重合,如图所示,
此时EF 的最小值为(CT=4.8.
5.(1)PG=PC,理由略 (2)①30°
(3)
(1)连接BP,由折叠的性质可得出∠MGB=∠A=90°,BG=AB,利用“HL”证明 Rt△BGP≌Rt△BCP,由全等三角形的性质即可得解;(2)①连接CG,证明△BCG为等边三角形,由等边三角形的性质得出∠GBF=60°,进而求得∠BGF=30°,根据平角的定义求出∠MGE 的度数,即可求解;②设出 EG的长度,分别表示出 AM,ME,DE的长度,证明△MEG∽△MDP,由相似三角形的性质即可求解;(3)设 AB=5a,BC=6a,证明△MEG∽△GFB,求出 ME,MD的长,再证明△MEG∽△MDP,由相似三角形的性质即可求解.
解:(1)PG=PC.理由如下:连接 BP,如图1.
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC.
将正方形纸片ABCD沿直线BM 折叠,
∴∠MGB=∠A=90°,BG=AB,
∴BG=BC.
在 Rt△BGP 和 Rt△BCP 中
∴Rt△BGP≌Rt△BCP(HL),
∴PG=PC.
(2)①连接CG,如图2.
∵EF为折痕,
∴FG是BC 的垂直平分线,
∴BG=CG,
由(1)知BG=BC,
∴BG=CG=BC,
∴△BCG为等边三角形,
∴∠GBF=60°.∴∠BGF=30°.
∵∠BGM=90°.
∴∠MGE=60°.
②设EG=x.∵∠EMG=30°,
∴AM=MG=2x,
∵EG∥DP,∴△MEG∽△MDP,
(3) .【解题过程】:
设AB=5a,BC=6a,
∴BF=CF=3a.
∵△ABM沿直线BM 折叠,
∴∠BGM=∠A=90°,BG=AB=5a,
∴EG=a.
∵∠MGE+∠BGF=90°,∠BGF+∠GBF=90°,
∴∠MGE=∠GBF,
∴△MEG∽△GFB,
∵EG∥DP,∴△MEG∽△MDP,
同课章节目录
