专题11 四边形与正多边形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 专题11 四边形与正多边形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 444.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
专题11 四边形与正多边形
1.平行四边形的定义、性质与判定
(1)定义:两组对边分别 的四边形叫作平行四边形.
(2)性质:对边平行;对边 ;对角相等;对角线互相平分,是 图形.
(3)判定方法:①两组对边分别 的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③有一组对边 且 的四边形是平行四边形;
④对角线 的四边形是平行四边形.
2.矩形的定义、性质与判定
(1)定义:有一个角是 的 叫作矩形.
(2)性质:矩形的对边 且 ;四个角都是 ;两条对角线互相 且 .
(3)判定方法:①有三个角都是 的四边形是矩形;②对角线 的平行四边形是矩形.
3.菱形的定义、性质与判定
(1)定义:有一组邻边 的平行四边形叫作菱形,菱形是 图形,也是 图形,它的对称轴就是它的两条 所在直线.
(2)性质:菱形的四条边都 ;两条对角线互相 ;每条对角线平分 .
(3)判定方法:①有一组邻边 的平行四边形是菱形;②对角线 的平行四边形是菱形;③四条边都 的四边形是菱形.
4.正方形的定义、性质与判定
(1)定义:有一个角是 且有一组邻边 的平行四边形是正方形.
(2)性质:除具有平行四边形、矩形、菱形的一切性质外,还具有对角线与边夹角为 的性质;面积等于 ,正方形既是 图形,也是 图形,它的对称轴有 .
(3)判定方法:有一组邻边 的矩形是正方形;有一个角是 的菱形是正方形;对角线 且 平分的四边形是正方形.
5.梯形
一组对边 ,另一组对边 的四边形叫作梯形.同一底上的 的梯形是等腰梯形;两对角线 的梯形是等腰梯形;两腰 的梯形是等腰梯形.有一个角是 的梯形是直角梯形.连接梯形的两腰 的连线叫作梯形的中位线;梯形的中位线 于两底,并且等于 的一半.
6.梯形的常见辅助线
(1)平移梯形的 ,使两腰和同一底上两底角会聚到一个三角形中.
(2)平移梯形的 .
(3)作梯形的 .
(4)延长 ,使延长部分等于上底长,再 上底端点和下底的延长终点.
(5)作一 的平行线,和下底的延长线相交.
(6)过一腰的 作另一腰的 ,和其中一底的延长线相交,和另一底相交.
(7)延长两腰使之相交.
7.正多边形
(1)如果多边形的各边都 ,各内角都 ,则称它为正多边形.(2)正n边形的内角和等于 ,任意多边形的外角和等于 .
实战演练
1.如图,在 ABCD中,一定正确的是 ( )
A. AD=CD B. AC=BD
C. AB=CD D. CD=BC
2.如图,在菱形ABCD中,对角线AC,BD 相交于点O,点 E 为CD 的中点.若OE=3,则菱形 ABCD 的周长为( )
A.6 B.12 C.24 D.48
3.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形 ABCDEF,若对角线 AD 的长约为8mm ,则正六边形 ABCDEF的边长为( )
A. 2mm
D. 4m m
4.如图,在正五边形ABCDE中,以 AB为边向内作正△ABF,则下列结论错误的是 ( )
A. AE=AF
B.∠EAF=∠CBF
C.∠F=∠EAF
D.∠C=∠E
5.如图,在正方形 ABCD中,对角线 AC,BD相交于点O. E,F 分别为AC,BD 上一点,且 OE=OF,连接 AF,BE,EF.若∠AFE=25°,则∠CBE 的度数为 ( )
A.50° B.55°
C.65° D.70°
6.下列多边形中,内角和最大的是 ( )
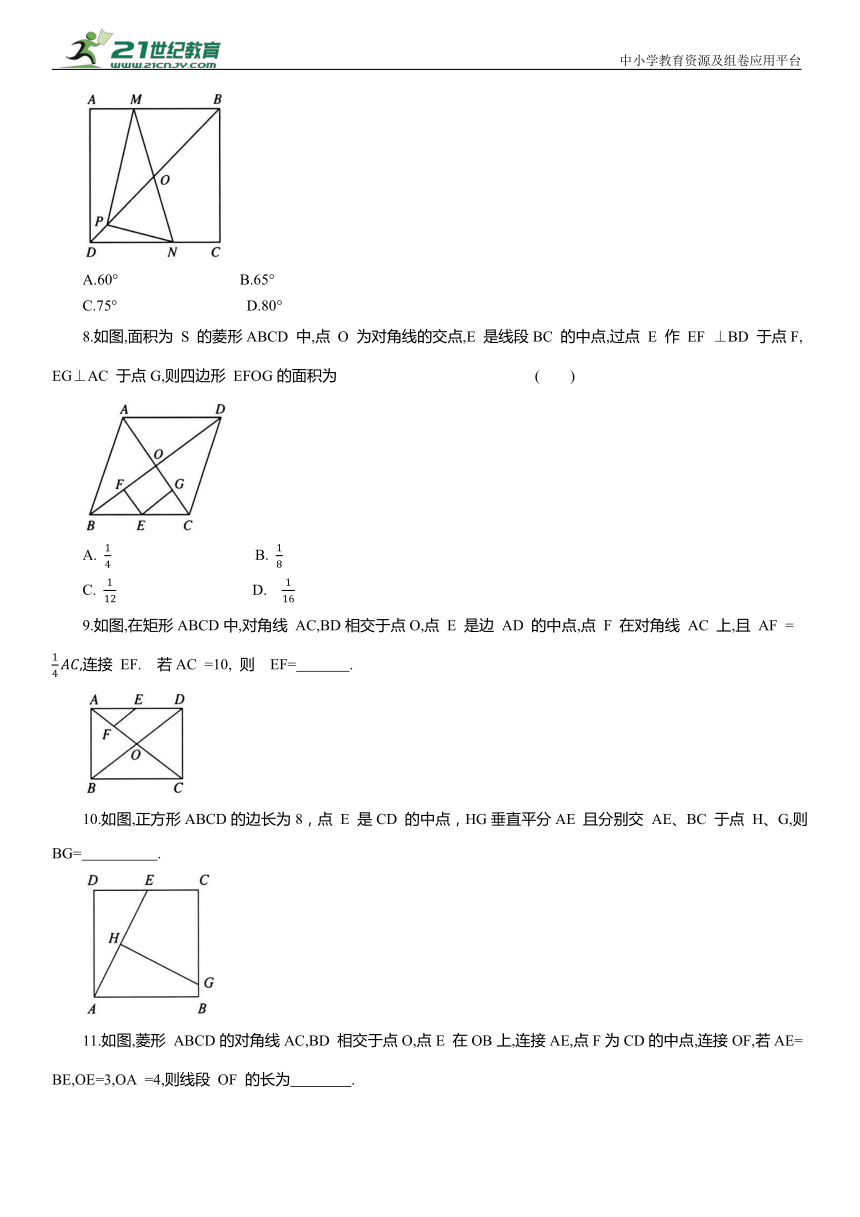
7.如图,把含 30°的直角三角板 PMN 放 置 在 正 方 形 ABCD 中,∠PMN = 30°, 直角顶 点 P 在 正方形ABCD 的对角线 BD 上,点 M,N 分别在AB 和CD 边上,MN 与 BD 交于点O,且点O为 MN 的中点,则∠AMP 的度数为( )
A.60° B.65°
C.75° D.80°
8.如图,面积为 S 的菱形ABCD 中,点 O 为对角线的交点,E 是线段BC 的中点,过点 E 作 EF ⊥BD 于点F,EG⊥AC 于点G,则四边形 EFOG的面积为 ( )
A. B.
C. D.
9.如图,在矩形ABCD中,对角线 AC,BD相交于点O,点 E 是边 AD 的中点,点 F 在对角线 AC 上,且 AF = 连接 EF. 若AC =10, 则 EF= .
10.如图,正方形ABCD的边长为8,点 E 是CD 的中点,HG垂直平分AE 且分别交 AE、BC 于点 H、G,则BG= .
11.如图,菱形 ABCD的对角线AC,BD 相交于点O,点E 在OB上,连接AE,点F为CD的中点,连接OF,若AE=BE,OE=3,OA =4,则线段 OF 的长为 .
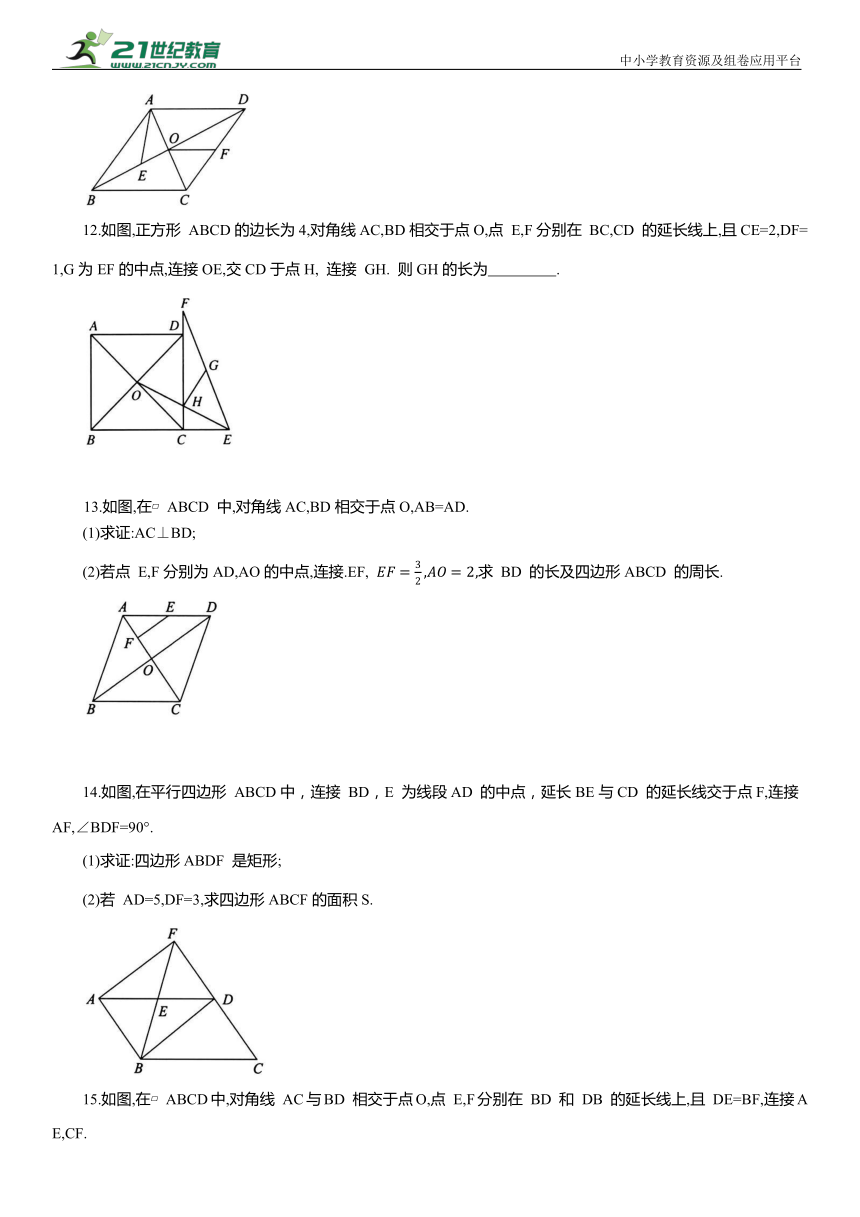
12.如图,正方形 ABCD的边长为4,对角线AC,BD相交于点O,点 E,F分别在 BC,CD 的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H, 连接 GH. 则GH的长为 .
13.如图,在 ABCD 中,对角线AC,BD相交于点O,AB=AD.
(1)求证:AC⊥BD;
(2)若点 E,F分别为AD,AO的中点,连接.EF, 求 BD 的长及四边形ABCD 的周长.
14.如图,在平行四边形 ABCD中,连接 BD,E 为线段AD 的中点,延长BE与CD 的延长线交于点F,连接 AF,∠BDF=90°.
(1)求证:四边形ABDF 是矩形;
(2)若 AD=5,DF=3,求四边形ABCF的面积S.
15.如图,在 ABCD中,对角线 AC与BD 相交于点O,点 E,F分别在 BD 和 DB 的延长线上,且 DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当 BD平分∠ABC时,四边形 AFCE 是什么特殊四边形 请说明理由.
如图,在正方形ABCD中,E 为 AB 边上一点,BF⊥CE于点G,若已知下列三角形面积,则可求阴影部分面积和的是( )
A. S△BAF B. S△BCF
C. S△BCG D. S△FCG
2.如图,在△ABC中,∠BAC=90°,以 BC为边向上作正方形 BCDE,以 AC为边作正方形ACFG,点 D 落在GF 上,连接 AE,EG.若 DG=2,BC=6,则△AEG 的面积为 ( )
A.4 B.6
D.8
3.如图,在平行四边形 ABCD 中,AB=2,AD=4,对角线 AC⊥AB,对角线 AC,BD交于点 O,点 E 为 BC 边中点,连接 OE,DE,则△DOE的面积为 ( )
C. D.2
4.如图,在菱形 ABCD 中,AB=4,∠B=120°,点 E,F 分别在边 AD,BC上,点 G,H 在对角线AC 上.若四边形 EGFH 是矩形,且FG∥AB,则EG的长是 ( )
A. B.1.5
C.2
5.问题:如图,在 ABCD中,点 E、点 F 在对角线AC上(不与点 A、点C重合),连接BE,DF.若 ,求证:BE=DF.在 ①AE = CF; ②∠ABE = ∠CDF;③∠BEC=∠DFA,这三个条件中选择其中一个,补充在上面问题中,并完成问题的解答.
注:如果选择多个条件分别解答,按第一个解答计分.
6.如图,在平行四边形 ABCD 中,点 O是对角线AC 中点,过点 O作EF⊥AC分别交边AB,CD于点E,F.
求证:四边形 AECF是菱形.
7.如图,在正方形 ABCD中,AC,BD 相交于点 O, 点 E, F 分 别 在 OA, OD 上,∠ABE=∠DCF.
(1)求证:△ABE≌△DCF;
(2)若 求 BE 的长.
8.如图,在等腰三角形ABC 中,AB=AC,点 D 是 BC 中点,点 E 是 AD 的中点,过点 A 作AF∥BC交BE 的延长线于点 F,连接CF.
(1)试判断四边形 ADCF 的形状,并加以证明;
(2)若AB=17,BC=30,求四边形 ADCF的面积.
参考答案
1.(1)平行
(2)相等 中心对称
(3)平行 平行 相等 互相平分
2.(1)直角 平行四边形
(2)相等 平行 直角 平分 相等
(3)直角 相等
3.(1)相等 中心对称 轴对称 对角线
(2)相等 垂直平分 每一组对角
(3)相等 互相垂直 相等
4.(1)直角 相等
(2)45° 边长的平方 轴对称 中心对称 四条
(3)相等 直角 相等 垂直
5.平行 不平行 两底角相等 相等 相等 直角 中点 平行 两底和
6.(1)腰
(2)对角线
(3)高
(4)下底 连接
(5)对角线
(6)中点 平行线
7.(1)相等 相等
(2)(n-2)·180° 360°
1. C 【解析】本题考查平行四边形的性质.根据平行四边形对边相等可得AB=CD,故选 C.
2. C 【解析】本题考查菱形的性质、三角形中位线定理.因为四边形ABCD是菱形,所以OA=OC.又E为CD的中点,所以 AD=2OE=6,所以菱形 ABCD 的周长为4AD=24,故选 C.
3. D 【解析】本题考查正六边形的性质、等边三角形的判定与性质.如图所示,连接CF,与AD交于点O.∵六边形ABCDEF 是正六边形,AD≈8 mm,∴∠AOF=60°, 是等边三角形,∴AF=故选 D.
4. C 【解析】本题考查正多边形的性质、多边形内角和定理.∵多边形 ABCDE 为正五边形,∴AB=AE,∠C= ∵△ABF是等边三角形,∴AB=AF,∠F=∠FAB=∠FBA=60°.对于 A,∵AB=AE,AB=AF,∴AE=AF,故 A 选 项 正确;对于 B,∵∠EAB =∠CBA,∠FAB=∠FBA,∴∠EAF=∠CBF,故B选项正确;对于C,∵∠F=60°,∠EAF=108°-60°=48°,∴∠F≠∠EAF,故C选项错误;对于D,∠C=∠E成立,故 D选项正确,故选C.
5. C 【解析】本题考查正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质.∵四边形ABCD是正方形,∴∠AOB=∠AOD=90°,OA=OB,∠OBC=45°. ∵ OE = OF, ∴ △OEF 为 等 腰 直 角 三 角 形,∴∠OEF=∠OFE=45°.∵∠AFE=25°,∴∠AFO=∠AFE+∠OFE=70°,∴∠FAO= 20°. 在△AOF 和△BOE 中, △BOE(SAS),∴∠EBO=∠FAO= 20°,∴∠CBE =∠EBO+∠OBC=65°,故选 C.
6. D 【解析】本题考查多边形的内角和.选项 A中的图形是一个三角形,其内角和为180°;选项 B中的图形是一个四边形,其内角和为360°;选项 C中的图形是一个五边形,其内角和为540°;选项 D中的图形是一个六边形,其内角和为720°,∴内角和最大的是六边形,故选 D.
7. C 【解析】本题考查正方形的性质、直角三角形的性质.在 Rt△PMN中,∠MPN=90°.因为O为MN 的中点,所以 因为∠PMN = 30°,所以∠MPO=30°,所以∠DPM=150°.在四边形 ADPM中,因为∠A = 90°,∠ADB= 45°,∠DPM = 150°, 所以∠AMP=360°-∠A-∠ADB-∠DPM=360°-90°- ,故选 C.
8. B 【解析】本题考查菱形的性质及面积公式、三角形中位线定理.∵四边形 ABCD 是菱形,∴BD垂直平分AC,设AC=4a,BD=4b,则 ∵E 为BC的中点,EF⊥OB 于点F,EG⊥OC 于点 G,∴四边形EFOG为矩形,∵OC=2a,OB=2b,∴EG=b,OG=a, 故选 B.
9. 【解析】本题考查矩形的性质、三角形的中位线定理.在矩形 ABCD中,BD=AC=10,∴OA=OD=5. ∴F 是AO 的中点.又∵E是AD 的中点,∴EF 是△AOD的中位线,
10.1 【解析】本题考查正方形的性质、线段垂直平分线的性质、勾股定理.如图,连接 AG,EG,在正方形 ABCD中,∠B=∠C=90°,CD=AB=BC=8.因为E 是CD的中点,所以 因为 HG垂直平分AE,所以 AG=EG.设 BG=x,在 Rt△ABG 中,. . 在 Rt△CEG 中, 所以( 解得x=1,即 BG=1.
11.2 【解析】本题考查勾股定理、三角形的中位线定理、菱形的性质.在菱形 ABCD中,AC⊥BD,AB=BC,OD=OB.在Rt△AOE中, 所以BE=AE=5,所以OB=BE+OE=8.在 Rt△AOB中, 所以 又因为 F为CD的中点,所以OF 为△BCD的中位线,所以
【解析】本题考查正方形的性质、全等三角形的判定与性质、勾股定理、三角形的中位线定理.如图,过点 O 作 OM ⊥CD,则 OM = CE = 2,∠OMH =∠ECH= 90°. 又 ∠OHM = ∠EHC, ∴△OHM≌△EHC,∴OH=EH,即 H 是OE 的中点.连接OF,∵G是 EF 的中点,∴GH 是△EFO 的中位线. 在Rt△OMF 中,FM= DM+ DF = 2 +1 = 3,∴OF = 即GH的长为
作辅助线构造全等三角形和直角三角形是解答本题的关键.
13.(1)略
(1)根据菱形的判定与性质即可证明;(2)由三角形的中位线定理求得OD,再由菱形的性质求得 BD,利用勾股定理求出AD,即可求解.
解:(1)证明:∵四边形 ABCD是平行四边形,且 AB=AD,∴ ABCD是菱形,
∴AC⊥BD.
(2)∵点 E,F分别为AD,AO的中点,
∴EF 是△AOD的中位线,
∴OD=2EF=3.
由(1)可知,四边形 ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,BD=2OD=6.
在 Rt△AOD中,由勾股定理得
∴菱形ABCD的周长为
14.(1)略 (2)18
(1)利用平行四边形的性质与“AAS”证明△ABE≌△DFE,则有AB=DF,结合AB∥DF与∠BDF=90°即可证明结论成立;(2)根据平行四边形与矩形的性质可得四边形 ABCF 的面积是△BDF 的面积的3倍,根据矩形的对边相等与勾股定理可得 BD 的长,求出△BDF 的面积,进而求出四边形 ABCF 的面积.
解:(1)证明:由四边形 ABCD 是平行四边形和已知得AB∥CF.
∴∠BAE=∠FDE,∠ABE=∠DFE.
∵E是AD 的中点,∴AE=DE.
∴△ABE≌△DFE(AAS).∴AB=DF.
∵AB∥CF,即AB∥DF,
∴四边形 ABDF 是平行四边形.
又∵∠BDF=90°,
∴四边形 ABDF 是矩形.
(2)∵四边形 ABCD 是平行四边形,四边形 ABDF 是矩形,
∴AB=CD=DF,即 D 是CF 的中点.
∴△BCD,△BDF,△ABF的面积相等.
∴四边形 ABCF 的面积S=3S△BDF.
∵AD=5,DF=3,四边形ABDF是矩形,
∴四边形 ABCF 的面积
15.(1)略 (2)菱形,理由略
(1)根据平行四边形的性质,利用 SAS 证明△ADE≌△CBF;(2)利用△ADE≌△CBF,得到 AE与CF 平行且相等,从而证明四边形 AFCE是平行四边形,再由角平分线的性质证明对角线互相垂直,从而证明四边形AFCE 是菱形.
解:(1)证明:∵四边形ABCD 是平行四边形,∴AD=BC,∠ADB=∠CBD.
又∵∠ADB+∠ADE=180°,
∠CBF+∠CBD=180°,
∴∠ADE=∠CBF.
在△ADE和△CBF中,AD=BC,
∠ADE=∠CBF,DE=BF,
∴△ADE≌△CBF(SAS).
(2)如图所示,连接AF,EC,
由(1)得△ADE≌△CBF则AE=CF,∠AED=∠CFB,
∴AE∥CF,
即AF⊥CE,
∴四边形 AFCE 是平行四边形,当 BD平分∠ABC时,∠ABD=∠CBD.
又∵AD∥CB,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
即AD=AB=BC,
∴△ABC为等腰三角形.
由等腰三角形三线合一的性质可知AC⊥EF,
∴平行四边形AFCE是菱形.
压轴预测
1. D 【解析】本题考查正方形的性质、全等三角形的判定及性质.在正方形 ABCD中,AB=BC=AD,∠BAD=∠ABC=90°.∵BF⊥CE,∴∠ABF+∠BEC=∠ABF+∠AFB= 90°,即∠BEC=∠AFB,∴△ABF≌△BCE,∴AF= BE,∴ AE = DF, ∴ S△AEC = S△CDF,∴S阴影 = 又: .若已知S△FCG,可求出阴影部分的面积和,故选D.
2. D 【解析】本题考查正方形的性质、全等三角形的判定与性质、三角形的面积公式.∵四边形 BCDE 是正方形,∴BC=CD,∠BCD=90°.∵四边形 ACFG 是正方形,
∴CF=AG= AC,∠ACF = 90°. 又∠ACB+∠ACD=∠ACD+∠FCD,∴∠ACB =∠FCD. 在△ABC 和△FDC 中,
∴AB=FD.过点 E 作 EH⊥BG 于点 H,则∠EBH=∠ACB,∠EHB=∠BAC=90°,BE= BC,∴△ABC≌△HEB(AAS),∴EH=AB.设 AB=a, 故选 D.
3. B 【解析】本题考查平行四边形的性质.∵四边形ABCD为平行四边形,∴BC=AD=4.在Rt△BAC中,AB = 2, BC = 4, 则 点O,E分别为 BD,BC 的中点, 故选 B.
4. A 【解析】本题考查菱形的性质、矩形的性质.如图,连接BD,交AC于点O,因为四边形 ABCD 是菱形,所以AC⊥BD,所以∠AOB=90°,因为∠ABC=120°,AB=BC,所!以 所以OB= 因为四边形 EGFH 是矩形,所以∠GFH=90°,因为 FG∥AB,所以∠FGH=∠BAC=30°,所以GH=2FH=2GE,即OG=GE,因为∠GFC=∠ABC=120°,∠GFH=90°,所以∠HFC=∠HCF=30°,所以 FH=HC,同理可得GE=AG,所以OA=AG+OG=2GE=2所以 故选 A.
中小学教育资源及组卷应用平台
5.略
根据题意,若选条件①,结合平行四边形的对边平行且相等,再由平行线得内错角相等,结合已知条件即可证明两个三角形全等,从而可得结论;若选条件②,结合平行四边形的对边平行且相等,再由平行线得内错角相等,结合已知条件,即可证明两个三角形全等,从而可得结论;若选条件③,结合平行四边形的对边平行且相等,再由平行线得内错角相等,结合已知条件,即可证明两个三角形全等,从而可得结论.
证明:若选条件①:
因为四边形ABCD是平行四边形,
所以AB=CD,AB∥CD,
所以∠BAE=∠DCF.
又因为AE=CF,
所以△ABE≌△CDF(SAS),
所以BE=DF.
若选条件②:
因为四边形ABCD 是平行四边形,
所以AB=CD,AB∥CD,
所以∠BAE=∠DCF.
又因为∠ABE=∠CDF,
所以△ABE≌△CDF(ASA),
所以BE=DF.
若选条件③:
因为四边形ABCD 是平行四边形,
所以BC=AD,AD∥BC,
所以∠BCE=∠DAF.
因为∠BEC=∠DFA,
所以△BCE≌△DAF(AAS),
所以BE=DF.
6.略
先利用线段垂直平分线的性质得对应边相等,然后根据等腰三角形三线合一的性质证明∠AFO=∠CFO,再根据内错角相等进行代换,可证明四边形 AECF 的四边相等,即可证明四边形 AECF 是菱形.
解:证明:∵EF⊥AC,OA=OC,
∴AF=CF,AE=CE,
∴∠AFO=∠CFO.
又∵四边形ABCD 为平行四边形,
∴AE∥CF,
∴∠CFO=∠AEF=∠AFO,
∴AF=AE=CE=CF,
∴四边形 AECF 是菱形.
7.(1)略 (2)
(1)根据正方形的性质与题中条件,结合“ASA”即可证明;(2)根据正方形的性质可得OB=OC=OA=4,再结合题中条件与勾股定理即可求出 BE的长.
解:(1)证明:在正方形ABCD中,AB=CD.
∵∠BAD=∠CDA=90°,
DB,AC分别平分∠CDA,∠BAD,
∴∠BAE=∠CDF=45°.
∵∠ABE=∠DCF,
∴△ABE≌△DCF(ASA).
(2)∵AC垂直平分BD,∠OBC=∠OCB=45°,
∴OB=OC=OA=4.
∵AE=3,
∴OE=1,
8.(1)矩形,证明略 (2)120
(1)由平行线得内错角相等,结合中点和对顶角相等,证明△AEF≌△DEB,得对边相等,再根据等腰三角形的性质证明∠ADC为90°和对边平行即可证明四边形是矩形;(2)根据已知线段的长,利用勾股定理求出 AD的长,即可求出矩形的面积.
解:(1)四边形 ADCF 是矩形.
证明:∵AF∥BC,
∴∠AFE=∠DBE.
∵点E是AD的中点,
∴AE=DE.
在△AEF 和△DEB中
∴△AEF≌△DEB(AAS),
∴AF=DB.
∵在等腰三角形 ABC中,点 D 是BC 的中点,
∴BD=CD,AD⊥BC,
∴AF=CD,∠ADC=90°.
∵AF∥BC,即AF∥CD,
∴四边形 ADCF 为矩形.
(2)∵BD=CD,BC=30,
∴BD=CD=15.
∵AB=AC=17,
∴在 Rt△ACD中,
∴S矩形ADCF=AD·CD=8×15=120.
1.平行四边形的定义、性质与判定
(1)定义:两组对边分别 的四边形叫作平行四边形.
(2)性质:对边平行;对边 ;对角相等;对角线互相平分,是 图形.
(3)判定方法:①两组对边分别 的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③有一组对边 且 的四边形是平行四边形;
④对角线 的四边形是平行四边形.
2.矩形的定义、性质与判定
(1)定义:有一个角是 的 叫作矩形.
(2)性质:矩形的对边 且 ;四个角都是 ;两条对角线互相 且 .
(3)判定方法:①有三个角都是 的四边形是矩形;②对角线 的平行四边形是矩形.
3.菱形的定义、性质与判定
(1)定义:有一组邻边 的平行四边形叫作菱形,菱形是 图形,也是 图形,它的对称轴就是它的两条 所在直线.
(2)性质:菱形的四条边都 ;两条对角线互相 ;每条对角线平分 .
(3)判定方法:①有一组邻边 的平行四边形是菱形;②对角线 的平行四边形是菱形;③四条边都 的四边形是菱形.
4.正方形的定义、性质与判定
(1)定义:有一个角是 且有一组邻边 的平行四边形是正方形.
(2)性质:除具有平行四边形、矩形、菱形的一切性质外,还具有对角线与边夹角为 的性质;面积等于 ,正方形既是 图形,也是 图形,它的对称轴有 .
(3)判定方法:有一组邻边 的矩形是正方形;有一个角是 的菱形是正方形;对角线 且 平分的四边形是正方形.
5.梯形
一组对边 ,另一组对边 的四边形叫作梯形.同一底上的 的梯形是等腰梯形;两对角线 的梯形是等腰梯形;两腰 的梯形是等腰梯形.有一个角是 的梯形是直角梯形.连接梯形的两腰 的连线叫作梯形的中位线;梯形的中位线 于两底,并且等于 的一半.
6.梯形的常见辅助线
(1)平移梯形的 ,使两腰和同一底上两底角会聚到一个三角形中.
(2)平移梯形的 .
(3)作梯形的 .
(4)延长 ,使延长部分等于上底长,再 上底端点和下底的延长终点.
(5)作一 的平行线,和下底的延长线相交.
(6)过一腰的 作另一腰的 ,和其中一底的延长线相交,和另一底相交.
(7)延长两腰使之相交.
7.正多边形
(1)如果多边形的各边都 ,各内角都 ,则称它为正多边形.(2)正n边形的内角和等于 ,任意多边形的外角和等于 .
实战演练
1.如图,在 ABCD中,一定正确的是 ( )
A. AD=CD B. AC=BD
C. AB=CD D. CD=BC
2.如图,在菱形ABCD中,对角线AC,BD 相交于点O,点 E 为CD 的中点.若OE=3,则菱形 ABCD 的周长为( )
A.6 B.12 C.24 D.48
3.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形 ABCDEF,若对角线 AD 的长约为8mm ,则正六边形 ABCDEF的边长为( )
A. 2mm
D. 4m m
4.如图,在正五边形ABCDE中,以 AB为边向内作正△ABF,则下列结论错误的是 ( )
A. AE=AF
B.∠EAF=∠CBF
C.∠F=∠EAF
D.∠C=∠E
5.如图,在正方形 ABCD中,对角线 AC,BD相交于点O. E,F 分别为AC,BD 上一点,且 OE=OF,连接 AF,BE,EF.若∠AFE=25°,则∠CBE 的度数为 ( )
A.50° B.55°
C.65° D.70°
6.下列多边形中,内角和最大的是 ( )
7.如图,把含 30°的直角三角板 PMN 放 置 在 正 方 形 ABCD 中,∠PMN = 30°, 直角顶 点 P 在 正方形ABCD 的对角线 BD 上,点 M,N 分别在AB 和CD 边上,MN 与 BD 交于点O,且点O为 MN 的中点,则∠AMP 的度数为( )
A.60° B.65°
C.75° D.80°
8.如图,面积为 S 的菱形ABCD 中,点 O 为对角线的交点,E 是线段BC 的中点,过点 E 作 EF ⊥BD 于点F,EG⊥AC 于点G,则四边形 EFOG的面积为 ( )
A. B.
C. D.
9.如图,在矩形ABCD中,对角线 AC,BD相交于点O,点 E 是边 AD 的中点,点 F 在对角线 AC 上,且 AF = 连接 EF. 若AC =10, 则 EF= .
10.如图,正方形ABCD的边长为8,点 E 是CD 的中点,HG垂直平分AE 且分别交 AE、BC 于点 H、G,则BG= .
11.如图,菱形 ABCD的对角线AC,BD 相交于点O,点E 在OB上,连接AE,点F为CD的中点,连接OF,若AE=BE,OE=3,OA =4,则线段 OF 的长为 .
12.如图,正方形 ABCD的边长为4,对角线AC,BD相交于点O,点 E,F分别在 BC,CD 的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H, 连接 GH. 则GH的长为 .
13.如图,在 ABCD 中,对角线AC,BD相交于点O,AB=AD.
(1)求证:AC⊥BD;
(2)若点 E,F分别为AD,AO的中点,连接.EF, 求 BD 的长及四边形ABCD 的周长.
14.如图,在平行四边形 ABCD中,连接 BD,E 为线段AD 的中点,延长BE与CD 的延长线交于点F,连接 AF,∠BDF=90°.
(1)求证:四边形ABDF 是矩形;
(2)若 AD=5,DF=3,求四边形ABCF的面积S.
15.如图,在 ABCD中,对角线 AC与BD 相交于点O,点 E,F分别在 BD 和 DB 的延长线上,且 DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当 BD平分∠ABC时,四边形 AFCE 是什么特殊四边形 请说明理由.
如图,在正方形ABCD中,E 为 AB 边上一点,BF⊥CE于点G,若已知下列三角形面积,则可求阴影部分面积和的是( )
A. S△BAF B. S△BCF
C. S△BCG D. S△FCG
2.如图,在△ABC中,∠BAC=90°,以 BC为边向上作正方形 BCDE,以 AC为边作正方形ACFG,点 D 落在GF 上,连接 AE,EG.若 DG=2,BC=6,则△AEG 的面积为 ( )
A.4 B.6
D.8
3.如图,在平行四边形 ABCD 中,AB=2,AD=4,对角线 AC⊥AB,对角线 AC,BD交于点 O,点 E 为 BC 边中点,连接 OE,DE,则△DOE的面积为 ( )
C. D.2
4.如图,在菱形 ABCD 中,AB=4,∠B=120°,点 E,F 分别在边 AD,BC上,点 G,H 在对角线AC 上.若四边形 EGFH 是矩形,且FG∥AB,则EG的长是 ( )
A. B.1.5
C.2
5.问题:如图,在 ABCD中,点 E、点 F 在对角线AC上(不与点 A、点C重合),连接BE,DF.若 ,求证:BE=DF.在 ①AE = CF; ②∠ABE = ∠CDF;③∠BEC=∠DFA,这三个条件中选择其中一个,补充在上面问题中,并完成问题的解答.
注:如果选择多个条件分别解答,按第一个解答计分.
6.如图,在平行四边形 ABCD 中,点 O是对角线AC 中点,过点 O作EF⊥AC分别交边AB,CD于点E,F.
求证:四边形 AECF是菱形.
7.如图,在正方形 ABCD中,AC,BD 相交于点 O, 点 E, F 分 别 在 OA, OD 上,∠ABE=∠DCF.
(1)求证:△ABE≌△DCF;
(2)若 求 BE 的长.
8.如图,在等腰三角形ABC 中,AB=AC,点 D 是 BC 中点,点 E 是 AD 的中点,过点 A 作AF∥BC交BE 的延长线于点 F,连接CF.
(1)试判断四边形 ADCF 的形状,并加以证明;
(2)若AB=17,BC=30,求四边形 ADCF的面积.
参考答案
1.(1)平行
(2)相等 中心对称
(3)平行 平行 相等 互相平分
2.(1)直角 平行四边形
(2)相等 平行 直角 平分 相等
(3)直角 相等
3.(1)相等 中心对称 轴对称 对角线
(2)相等 垂直平分 每一组对角
(3)相等 互相垂直 相等
4.(1)直角 相等
(2)45° 边长的平方 轴对称 中心对称 四条
(3)相等 直角 相等 垂直
5.平行 不平行 两底角相等 相等 相等 直角 中点 平行 两底和
6.(1)腰
(2)对角线
(3)高
(4)下底 连接
(5)对角线
(6)中点 平行线
7.(1)相等 相等
(2)(n-2)·180° 360°
1. C 【解析】本题考查平行四边形的性质.根据平行四边形对边相等可得AB=CD,故选 C.
2. C 【解析】本题考查菱形的性质、三角形中位线定理.因为四边形ABCD是菱形,所以OA=OC.又E为CD的中点,所以 AD=2OE=6,所以菱形 ABCD 的周长为4AD=24,故选 C.
3. D 【解析】本题考查正六边形的性质、等边三角形的判定与性质.如图所示,连接CF,与AD交于点O.∵六边形ABCDEF 是正六边形,AD≈8 mm,∴∠AOF=60°, 是等边三角形,∴AF=故选 D.
4. C 【解析】本题考查正多边形的性质、多边形内角和定理.∵多边形 ABCDE 为正五边形,∴AB=AE,∠C= ∵△ABF是等边三角形,∴AB=AF,∠F=∠FAB=∠FBA=60°.对于 A,∵AB=AE,AB=AF,∴AE=AF,故 A 选 项 正确;对于 B,∵∠EAB =∠CBA,∠FAB=∠FBA,∴∠EAF=∠CBF,故B选项正确;对于C,∵∠F=60°,∠EAF=108°-60°=48°,∴∠F≠∠EAF,故C选项错误;对于D,∠C=∠E成立,故 D选项正确,故选C.
5. C 【解析】本题考查正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质.∵四边形ABCD是正方形,∴∠AOB=∠AOD=90°,OA=OB,∠OBC=45°. ∵ OE = OF, ∴ △OEF 为 等 腰 直 角 三 角 形,∴∠OEF=∠OFE=45°.∵∠AFE=25°,∴∠AFO=∠AFE+∠OFE=70°,∴∠FAO= 20°. 在△AOF 和△BOE 中, △BOE(SAS),∴∠EBO=∠FAO= 20°,∴∠CBE =∠EBO+∠OBC=65°,故选 C.
6. D 【解析】本题考查多边形的内角和.选项 A中的图形是一个三角形,其内角和为180°;选项 B中的图形是一个四边形,其内角和为360°;选项 C中的图形是一个五边形,其内角和为540°;选项 D中的图形是一个六边形,其内角和为720°,∴内角和最大的是六边形,故选 D.
7. C 【解析】本题考查正方形的性质、直角三角形的性质.在 Rt△PMN中,∠MPN=90°.因为O为MN 的中点,所以 因为∠PMN = 30°,所以∠MPO=30°,所以∠DPM=150°.在四边形 ADPM中,因为∠A = 90°,∠ADB= 45°,∠DPM = 150°, 所以∠AMP=360°-∠A-∠ADB-∠DPM=360°-90°- ,故选 C.
8. B 【解析】本题考查菱形的性质及面积公式、三角形中位线定理.∵四边形 ABCD 是菱形,∴BD垂直平分AC,设AC=4a,BD=4b,则 ∵E 为BC的中点,EF⊥OB 于点F,EG⊥OC 于点 G,∴四边形EFOG为矩形,∵OC=2a,OB=2b,∴EG=b,OG=a, 故选 B.
9. 【解析】本题考查矩形的性质、三角形的中位线定理.在矩形 ABCD中,BD=AC=10,∴OA=OD=5. ∴F 是AO 的中点.又∵E是AD 的中点,∴EF 是△AOD的中位线,
10.1 【解析】本题考查正方形的性质、线段垂直平分线的性质、勾股定理.如图,连接 AG,EG,在正方形 ABCD中,∠B=∠C=90°,CD=AB=BC=8.因为E 是CD的中点,所以 因为 HG垂直平分AE,所以 AG=EG.设 BG=x,在 Rt△ABG 中,. . 在 Rt△CEG 中, 所以( 解得x=1,即 BG=1.
11.2 【解析】本题考查勾股定理、三角形的中位线定理、菱形的性质.在菱形 ABCD中,AC⊥BD,AB=BC,OD=OB.在Rt△AOE中, 所以BE=AE=5,所以OB=BE+OE=8.在 Rt△AOB中, 所以 又因为 F为CD的中点,所以OF 为△BCD的中位线,所以
【解析】本题考查正方形的性质、全等三角形的判定与性质、勾股定理、三角形的中位线定理.如图,过点 O 作 OM ⊥CD,则 OM = CE = 2,∠OMH =∠ECH= 90°. 又 ∠OHM = ∠EHC, ∴△OHM≌△EHC,∴OH=EH,即 H 是OE 的中点.连接OF,∵G是 EF 的中点,∴GH 是△EFO 的中位线. 在Rt△OMF 中,FM= DM+ DF = 2 +1 = 3,∴OF = 即GH的长为
作辅助线构造全等三角形和直角三角形是解答本题的关键.
13.(1)略
(1)根据菱形的判定与性质即可证明;(2)由三角形的中位线定理求得OD,再由菱形的性质求得 BD,利用勾股定理求出AD,即可求解.
解:(1)证明:∵四边形 ABCD是平行四边形,且 AB=AD,∴ ABCD是菱形,
∴AC⊥BD.
(2)∵点 E,F分别为AD,AO的中点,
∴EF 是△AOD的中位线,
∴OD=2EF=3.
由(1)可知,四边形 ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,BD=2OD=6.
在 Rt△AOD中,由勾股定理得
∴菱形ABCD的周长为
14.(1)略 (2)18
(1)利用平行四边形的性质与“AAS”证明△ABE≌△DFE,则有AB=DF,结合AB∥DF与∠BDF=90°即可证明结论成立;(2)根据平行四边形与矩形的性质可得四边形 ABCF 的面积是△BDF 的面积的3倍,根据矩形的对边相等与勾股定理可得 BD 的长,求出△BDF 的面积,进而求出四边形 ABCF 的面积.
解:(1)证明:由四边形 ABCD 是平行四边形和已知得AB∥CF.
∴∠BAE=∠FDE,∠ABE=∠DFE.
∵E是AD 的中点,∴AE=DE.
∴△ABE≌△DFE(AAS).∴AB=DF.
∵AB∥CF,即AB∥DF,
∴四边形 ABDF 是平行四边形.
又∵∠BDF=90°,
∴四边形 ABDF 是矩形.
(2)∵四边形 ABCD 是平行四边形,四边形 ABDF 是矩形,
∴AB=CD=DF,即 D 是CF 的中点.
∴△BCD,△BDF,△ABF的面积相等.
∴四边形 ABCF 的面积S=3S△BDF.
∵AD=5,DF=3,四边形ABDF是矩形,
∴四边形 ABCF 的面积
15.(1)略 (2)菱形,理由略
(1)根据平行四边形的性质,利用 SAS 证明△ADE≌△CBF;(2)利用△ADE≌△CBF,得到 AE与CF 平行且相等,从而证明四边形 AFCE是平行四边形,再由角平分线的性质证明对角线互相垂直,从而证明四边形AFCE 是菱形.
解:(1)证明:∵四边形ABCD 是平行四边形,∴AD=BC,∠ADB=∠CBD.
又∵∠ADB+∠ADE=180°,
∠CBF+∠CBD=180°,
∴∠ADE=∠CBF.
在△ADE和△CBF中,AD=BC,
∠ADE=∠CBF,DE=BF,
∴△ADE≌△CBF(SAS).
(2)如图所示,连接AF,EC,
由(1)得△ADE≌△CBF则AE=CF,∠AED=∠CFB,
∴AE∥CF,
即AF⊥CE,
∴四边形 AFCE 是平行四边形,当 BD平分∠ABC时,∠ABD=∠CBD.
又∵AD∥CB,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
即AD=AB=BC,
∴△ABC为等腰三角形.
由等腰三角形三线合一的性质可知AC⊥EF,
∴平行四边形AFCE是菱形.
压轴预测
1. D 【解析】本题考查正方形的性质、全等三角形的判定及性质.在正方形 ABCD中,AB=BC=AD,∠BAD=∠ABC=90°.∵BF⊥CE,∴∠ABF+∠BEC=∠ABF+∠AFB= 90°,即∠BEC=∠AFB,∴△ABF≌△BCE,∴AF= BE,∴ AE = DF, ∴ S△AEC = S△CDF,∴S阴影 = 又: .若已知S△FCG,可求出阴影部分的面积和,故选D.
2. D 【解析】本题考查正方形的性质、全等三角形的判定与性质、三角形的面积公式.∵四边形 BCDE 是正方形,∴BC=CD,∠BCD=90°.∵四边形 ACFG 是正方形,
∴CF=AG= AC,∠ACF = 90°. 又∠ACB+∠ACD=∠ACD+∠FCD,∴∠ACB =∠FCD. 在△ABC 和△FDC 中,
∴AB=FD.过点 E 作 EH⊥BG 于点 H,则∠EBH=∠ACB,∠EHB=∠BAC=90°,BE= BC,∴△ABC≌△HEB(AAS),∴EH=AB.设 AB=a, 故选 D.
3. B 【解析】本题考查平行四边形的性质.∵四边形ABCD为平行四边形,∴BC=AD=4.在Rt△BAC中,AB = 2, BC = 4, 则 点O,E分别为 BD,BC 的中点, 故选 B.
4. A 【解析】本题考查菱形的性质、矩形的性质.如图,连接BD,交AC于点O,因为四边形 ABCD 是菱形,所以AC⊥BD,所以∠AOB=90°,因为∠ABC=120°,AB=BC,所!以 所以OB= 因为四边形 EGFH 是矩形,所以∠GFH=90°,因为 FG∥AB,所以∠FGH=∠BAC=30°,所以GH=2FH=2GE,即OG=GE,因为∠GFC=∠ABC=120°,∠GFH=90°,所以∠HFC=∠HCF=30°,所以 FH=HC,同理可得GE=AG,所以OA=AG+OG=2GE=2所以 故选 A.
中小学教育资源及组卷应用平台
5.略
根据题意,若选条件①,结合平行四边形的对边平行且相等,再由平行线得内错角相等,结合已知条件即可证明两个三角形全等,从而可得结论;若选条件②,结合平行四边形的对边平行且相等,再由平行线得内错角相等,结合已知条件,即可证明两个三角形全等,从而可得结论;若选条件③,结合平行四边形的对边平行且相等,再由平行线得内错角相等,结合已知条件,即可证明两个三角形全等,从而可得结论.
证明:若选条件①:
因为四边形ABCD是平行四边形,
所以AB=CD,AB∥CD,
所以∠BAE=∠DCF.
又因为AE=CF,
所以△ABE≌△CDF(SAS),
所以BE=DF.
若选条件②:
因为四边形ABCD 是平行四边形,
所以AB=CD,AB∥CD,
所以∠BAE=∠DCF.
又因为∠ABE=∠CDF,
所以△ABE≌△CDF(ASA),
所以BE=DF.
若选条件③:
因为四边形ABCD 是平行四边形,
所以BC=AD,AD∥BC,
所以∠BCE=∠DAF.
因为∠BEC=∠DFA,
所以△BCE≌△DAF(AAS),
所以BE=DF.
6.略
先利用线段垂直平分线的性质得对应边相等,然后根据等腰三角形三线合一的性质证明∠AFO=∠CFO,再根据内错角相等进行代换,可证明四边形 AECF 的四边相等,即可证明四边形 AECF 是菱形.
解:证明:∵EF⊥AC,OA=OC,
∴AF=CF,AE=CE,
∴∠AFO=∠CFO.
又∵四边形ABCD 为平行四边形,
∴AE∥CF,
∴∠CFO=∠AEF=∠AFO,
∴AF=AE=CE=CF,
∴四边形 AECF 是菱形.
7.(1)略 (2)
(1)根据正方形的性质与题中条件,结合“ASA”即可证明;(2)根据正方形的性质可得OB=OC=OA=4,再结合题中条件与勾股定理即可求出 BE的长.
解:(1)证明:在正方形ABCD中,AB=CD.
∵∠BAD=∠CDA=90°,
DB,AC分别平分∠CDA,∠BAD,
∴∠BAE=∠CDF=45°.
∵∠ABE=∠DCF,
∴△ABE≌△DCF(ASA).
(2)∵AC垂直平分BD,∠OBC=∠OCB=45°,
∴OB=OC=OA=4.
∵AE=3,
∴OE=1,
8.(1)矩形,证明略 (2)120
(1)由平行线得内错角相等,结合中点和对顶角相等,证明△AEF≌△DEB,得对边相等,再根据等腰三角形的性质证明∠ADC为90°和对边平行即可证明四边形是矩形;(2)根据已知线段的长,利用勾股定理求出 AD的长,即可求出矩形的面积.
解:(1)四边形 ADCF 是矩形.
证明:∵AF∥BC,
∴∠AFE=∠DBE.
∵点E是AD的中点,
∴AE=DE.
在△AEF 和△DEB中
∴△AEF≌△DEB(AAS),
∴AF=DB.
∵在等腰三角形 ABC中,点 D 是BC 的中点,
∴BD=CD,AD⊥BC,
∴AF=CD,∠ADC=90°.
∵AF∥BC,即AF∥CD,
∴四边形 ADCF 为矩形.
(2)∵BD=CD,BC=30,
∴BD=CD=15.
∵AB=AC=17,
∴在 Rt△ACD中,
∴S矩形ADCF=AD·CD=8×15=120.
同课章节目录
