专题13 图形的变换 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 专题13 图形的变换 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 693.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
专题13 图形的变换
1.图形的平移
(1) 定义: 在平面内, 将一个图形 移动一定的 ,这样的图形的运动叫作平移.
(2)性质:新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是 ,连接各组对应点的线段 且 .
(3)平移图形的作图依据: ; ; .因此在平移作图时,应依照指定的 、 画图,采用“以局部带整体”的平移方法,即通过几个 平移后的 ,得到平移的图形.
2.轴对称
(1)如果一个图形沿一条直线对折,对折后的两部分能 ,那么这个图形就是 ,这条直线就是它的 .
(2)如果一个图形沿一条直线折叠,如果它能与另一个图形 ,那么这两个图形成 ,这条直线是 ,折叠后重合的对应点就是 .
(3)如果两个图形关于 对称,那么对称轴是任何一对对应点所连线段的 .
3.旋转
(1)把一个图形 的图形变换叫作旋转, 叫作旋转中心, 叫作旋转角.
中小学教育资源及组卷应用平台
(2)图形的旋转由 、 和 所决定.其中① 在旋转过程中保持不动; ②旋 转 分为 时针 和 时针; ③旋转 一般小于 360°.
(3)旋转的特征:图形中每一点都绕着 旋转了 的角度,对应点到旋转中心的 相等,对应 相等,对应 相等,图形的 都没有发生变化,也就是旋转前后的两个图形为 .
(4)旋转作图的依据: 相等,对应点到旋转中心的 相等.旋转作图时,在确定了 后,依据指定的 和 画图,具体操作时往往通过 旋转后的位置,得到旋转后的图形.
4.中心对称
(1) 把一个图形绕着某一个点旋转 °,如果旋转后的图形能够与原来的图形 ,那么这个图形叫作 图形,这个点就是它的 .
(2)把一个图形绕着某一个点旋转 °, 如果它能够与另一个图形 ,那么就说这两个图形关于这个点成 ,这个点叫作 .这两个图形中的对应点叫作关于中心的 .
(3)关于中心对称的两个图形,对称点所连线段都经过 ,而且被对称中心所 .关于中心对称的两个图形是 图形.识别一个图形是否是中心对称图形,其依据是中心对称图形的定义,看其绕 后是否与其本身重合.若重合,则说明是中心对称图形;反之,则不是.
5.位似
(1)如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,像这样的两个图形叫作 ,这点叫作 ,也就是说这两个图形关于这点 ,它们的相似比又称 .
(2)位似图形上任意一对对应点到位似中心的距离之比等于 .
(3)在平面直角坐标系中,如果 是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的 比等于 或 .
实战演练
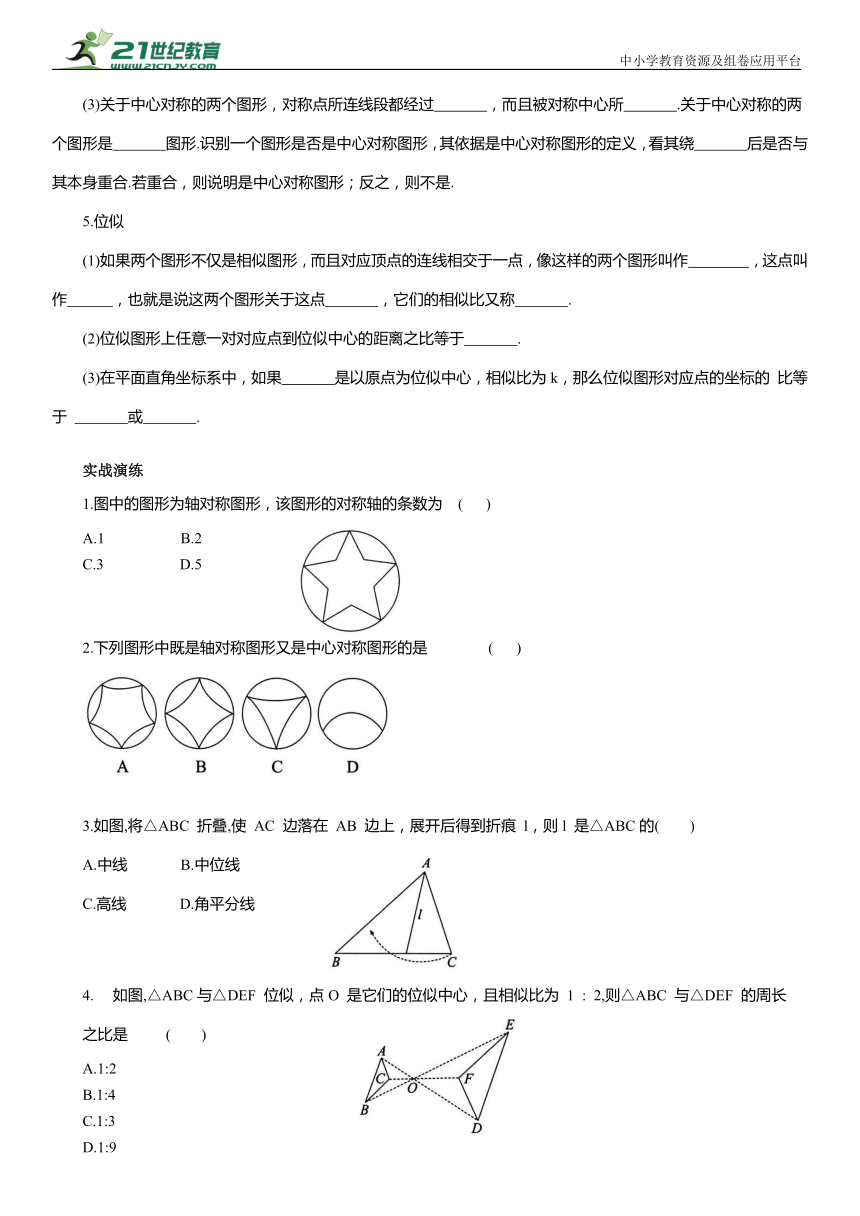
1.图中的图形为轴对称图形,该图形的对称轴的条数为 ( )
A.1 B.2
C.3 D.5
2.下列图形中既是轴对称图形又是中心对称图形的是 ( )
3.如图,将△ABC 折叠,使 AC 边落在 AB 边上,展开后得到折痕 l,则l 是△ABC的( )
A.中线 B.中位线
C.高线 D.角平分线
如图,△ABC与△DEF 位似,点O 是它们的位似中心,且相似比为 1 : 2,则△ABC 与△DEF 的周长
之比是 ( )
A.1:2
B.1:4
C.1:3
D.1:9
5.如图,在△ABC 中,AB=AC,若 M 是 BC 边上任意一 点, 将 △ABM 绕点A 逆时针旋转得到△ACN,点 M 的对应点为点 N,连接 MN,则下列结论一定正确的是 ( )
A. AB=AN
B. AB∥NC
C.∠AMN=∠ACN
D. MN⊥AC
6.如图,在△ABC中,∠ACB=90°,将△ABC绕点 C顺 时 针 旋 转 得 到△DEC,使点 B 的对应点 E 恰好落在边AC 上,点A 的对应点为D,延长 DE交AB 于点 F,则下列结论一定正确的是 ( )
A. AC=DE B. BC=EF
C.∠AEF=∠D D. AB⊥DF
7.如图,在平面直角坐标系中,△ABC 的顶点 A,B 的坐标分别是A(0,2),B(2,--1),平移△ABC 得到△A'B'C',若点 A 的对应点 A'的坐标为(--1,0),则 点 B 的 对 应 点 B' 的 坐 标是 .
8.如图, △ABC 中,点 D 为边 BC 的中点,连接AD,将△ADC 沿 直 线AD 翻 折 至 △ABC 所 在 平 面 内, 得△ADC',连接 CC',分别与边 AB 交于点E,与AD交于点O.若AE=BE,BC'=2,则AD的长为 .
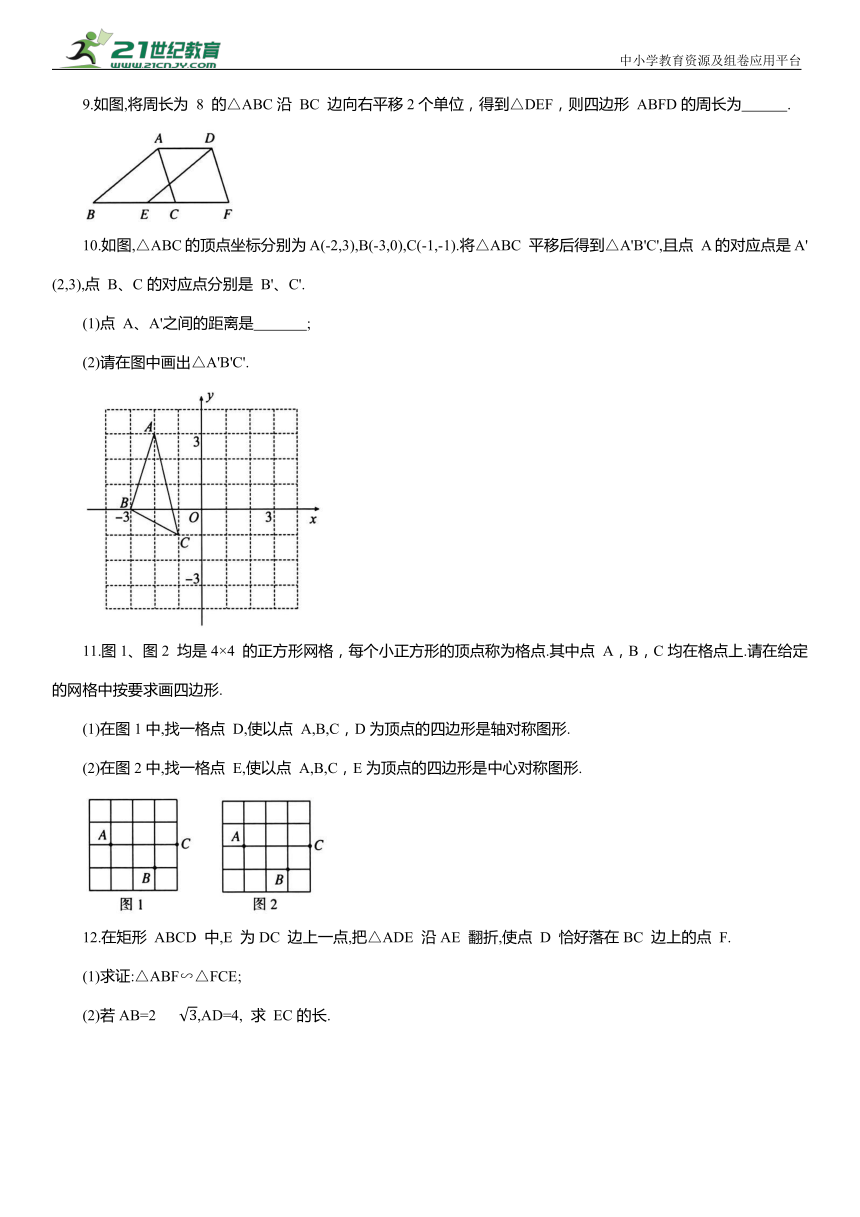
9.如图,将周长为 8 的△ABC沿 BC 边向右平移2个单位,得到△DEF,则四边形 ABFD的周长为 .
10.如图,△ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将△ABC 平移后得到△A'B'C',且点 A的对应点是A'(2,3),点 B、C的对应点分别是 B'、C'.
(1)点 A、A'之间的距离是 ;
(2)请在图中画出△A'B'C'.
11.图1、图2 均是4×4 的正方形网格,每个小正方形的顶点称为格点.其中点 A,B,C均在格点上.请在给定的网格中按要求画四边形.
(1)在图1中,找一格点 D,使以点 A,B,C,D为顶点的四边形是轴对称图形.
(2)在图2中,找一格点 E,使以点 A,B,C,E为顶点的四边形是中心对称图形.
12.在矩形 ABCD 中,E 为DC 边上一点,把△ADE 沿AE 翻折,使点 D 恰好落在BC 边上的点 F.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4, 求 EC的长.
压轴预测
1.如图,在平面直角坐标系中,A(0,1),B(-1,0),C(1,0),请确定一点 D,使得以点 A,B,C,D为顶点的四边形是轴对称图形但不是中心对称图形,则点 D 的坐标可能是 ( )
A.(0,-1)
B.(2,1)
C.(0,-2)
D.(-1,1)
2.如图,在 Rt△ABC 中,∠B=90°,AB=12,AC=13.现将纸片进行折叠,使得顶点 B 落在AC 边上,对应点为 D,折痕为AE.则 BE的长为 ( )
A.2.4 B.2.5
C.2.8 D.3
3.如图是一张矩形纸片 ABCD,点 E 在AB边上,把△ADE 沿直线 DE 折叠,使点 A落在BC 边上的点 F 处.点 G 在 BC 边上,把△CDG沿直线 DG 折叠,使点 C 恰好落在 线 段 DF 上 的 点 H 处,∠EDG = °. 若 则
4.图1、图2均为7×6 的正方形网格,点 A,B,C在格点上.
(1)在图1中确定格点 D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形.(画一个即可)
(2)在图2中确定格点 E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形.(画一个即可)
5.在4×4的方格中,选择6个小方格涂上阴影,请仔细观察图1中的六个图案的对称性,按要求回答.
(1)请在六个图案中,选出三个具有相同对称性的图案.
选出的三个图案是 (填写序号);它们都是 图形(填写“中心对称”或“轴对称”);
(2)请在图2中,将1个小方格涂上阴影,使整个4×4的方格也具有(1)中所选图案相同的对称性.
6.如图,△ABC 的三个顶点坐标分别是A(0,3),B(1,0),C(3,1).
(1)以原点O 为位似中心,在y轴左侧画出△A B C ,使得△A B C 与△ABC 的位似比为2:1;
(2)△ABC 的内部一点 M 的坐标为(a,b),则点 M 在△A B C 中的对应点 M1的坐标是多少
7.如图,△ABC的三个顶点坐标分别为A(1,1),B(4,2),C(3,5).
(1)以O为旋转中心,将△ABC逆时针旋转90°得到△A B C ;
(2)将△ABC平移,使平移后点 B,C的对应点B2,C2分别在 y轴和x 轴上,画出平移后的△A B C ;
(3) 借助网格,利用无刻度直尺 画出△A B C 的中线C2D2.
参考答案
1.(1)沿某一方向 距离
(2)对应点 相等 平行(或在同一直线上)
(3)平移不改变图形的大小和形状 对应角相等 对应点所连的线段平行(或在同一直线上)且相等 方向 距离关键点 位置
2.(1)重合 轴对称图形 对称轴
(2)重合 轴对称 对称轴 对称点
(3)某直线 垂直平分线
3.(1)绕某一点O转动一个角度 点 O转动的角
(2)旋转中心 旋转方向 旋转角度旋转中心 方向 顺 逆 角度
(3)旋转中心 相同 距离 夹角 线段 形状与大小 全等图形
(4)旋转角 距离 旋转中心 旋转方向 旋转角度 几个关键点
4.(1)180 重合 中心对称 对称中心
(2)180 重合 中心对称 对称中心对称点
(3)对称中心 平分 全等 某一点旋转 180°
5.(1)位似图形 位似中心 位似 位似比
(2)位似比
(3)位似变换 k - k
1. D 【解析】本题考查轴对称图形的对称轴条数.如图,作出该图形的对称轴,其条数为5,故选 D.
2. B
3. D 【解析】本题考查轴对称的性质.由折叠知折痕平分∠BAC,故选 D.
4. A 【解析】本题考查位似的性质.△ABC 与△DEF 的周长之比与位似比相等,即为1:2,故选 A.
5. C
6. D 【解析】本题考查图形旋转的性质.由旋转的性质得AC= DC,BC=EC,∠A=∠D,又∠AEF=∠DEC,∴∠AFE=∠DCE=90°,∴AB⊥DF,∴一定正确的是D选项,故选 D.
7.(1,-3) 【解析】本题考查平移的性质.因为点 A 从(0,2)平移至 A'(-1,0),所以△ABC先向下平移2个单位长度,再向左平移1个单位长度,所以点 B(2,-1)平移后的对应点 B'的坐标为(1,-3).
8.3 【解析】本题考查翻折的性质、三角形的中位线定理、全等三角形的判定与性质.由翻折的性质可知△DCA≌△DC'A,OC=OC',∠COD=∠C'OD=90°,所以 O为CC'的中点.因为 D为BC 的中点,所以OD 是△BCC'的中位线,所以OD= BC',OD∥BC',所以∠COD= 因为 AE=BE,BC'=2,所以OD=1.在△EC' B 和 △EOA 中, 所 以△EC'B≌△EOA(AAS),所以. 所以 AO=2,所以AD=AO+OD=2+1=3.
9.12 【解析】本题考查图形的平移.∵平移的距离为 2个单位长度,∴AD=CF=2.又∵AC=DF,∴四边形ABFD的周长为8+2+2=12.
10.(1)4 (2)图略
解:(1)4.
(2)如图,△A'B'C'即为所求作.
11.(1)略 (2)略
(1)以AC为对称轴,作点 B的对称点 D,则四边形 ABCD即为所求;或以 BC的垂直平分线为对称轴,作点 A 的对称点 D,则四边形 ABCD 即为所求;或以 AC的垂直平分线为对称轴,作点 B的对称点D,则四边形ABCD即为所求;(2)以AC为对角线或以AC 为边作平行四边形即可.
解:答案不唯一,以下答案供参考:
评分说明:(1)未标注点 D,E或标注错误,但所画图形正确不扣分.
(2)作图痕迹是虚线不扣分.
(3)点的位置正确但没画四边形共扣1分.
(4)第(1)问和第(2)问只画对一个给3分.
12.(1)略
(1)根据两角对应相等的两个三角形相似即可证明;
(2)设CE=x,由 △ABF∽△FCE,可得 ∠CFE =∠BAF=30°,进而得EF=2x,由此即可求解.
解:(1)由题意得∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°.
又∵∠EFC+∠FEC=90°,
∴∠AFB=∠FEC.
又∵∠B=∠C,
∴△ABF∽△FCE.
∴AF=4且∠BAF=30°.
又∵△ABF∽△FCE,
∴∠CFE=∠BAF=30°.
设CE=x,
则EF=2x,
压轴预测
1. C 【解析】本题考查中心对称图形和轴对称图形.分别在坐标系中描出选项中的各点,观察所得的图形,可知点(0,-2)与A,B,C三点构成的四边形是轴对称图形但不是中心对称图形,故选 C.
2. A 【解析】本题考查折叠的性质、勾股定理的应用.∵∠B=90°,AC=13,AB=12,∴BC=√AC -AB =5.设BE=x.由折叠的性质,可得AD=AB=12,DE=BE=x,∠ADE=∠B=90°,∴CD=AC-AD=13-12=1,EC=BC-BE=5-x.在 Rt△DEC中, DE ,即( 解得x=2.4,∴BE=2.4,故选 A.
3.45 【解析】本题考查矩形的性质、轴对称的性质、锐角三角函数.在矩形 ABCD 中,∠ADC=90°,由折叠
可知,∠ADE=∠EDH,∠HDG=∠GDC,∴∠EDH+ 即∠EDG=45°;∵BF+CG= 即
4.(1)略 (2)略
解:(1)画出符合要求的图形如下.(答案不唯一)
(2)画出符合要求的图形如下.(答案不唯一)
5.(1)①③⑤ 轴对称(或②④⑥ 中心对称) (2)略
解:(1)①③⑤轴对称(或②④⑥ 中心对称)
(2)轴对称
中心对称
6.(1)略 (2)(-2a,-2b)
(1)依据位似中心及位似比的大小即可作出△A B C ;
(2)根据位似比和位似图形的位置即可求解.
解:(1)如图所示,△A B C 即为所求.
(2)∵△A B C 与△ABC 的位似比为2 :1,△A B C 在 y轴左侧,△ABC的内部一点M 的坐标为(a,b),
则点 M 在 △A B C 中 的 对 应 点 M 的 坐 标是(-2a,-2b).
7.略
解:(1)如图.
(2)如图.
(3)如图.
1.图形的平移
(1) 定义: 在平面内, 将一个图形 移动一定的 ,这样的图形的运动叫作平移.
(2)性质:新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是 ,连接各组对应点的线段 且 .
(3)平移图形的作图依据: ; ; .因此在平移作图时,应依照指定的 、 画图,采用“以局部带整体”的平移方法,即通过几个 平移后的 ,得到平移的图形.
2.轴对称
(1)如果一个图形沿一条直线对折,对折后的两部分能 ,那么这个图形就是 ,这条直线就是它的 .
(2)如果一个图形沿一条直线折叠,如果它能与另一个图形 ,那么这两个图形成 ,这条直线是 ,折叠后重合的对应点就是 .
(3)如果两个图形关于 对称,那么对称轴是任何一对对应点所连线段的 .
3.旋转
(1)把一个图形 的图形变换叫作旋转, 叫作旋转中心, 叫作旋转角.
中小学教育资源及组卷应用平台
(2)图形的旋转由 、 和 所决定.其中① 在旋转过程中保持不动; ②旋 转 分为 时针 和 时针; ③旋转 一般小于 360°.
(3)旋转的特征:图形中每一点都绕着 旋转了 的角度,对应点到旋转中心的 相等,对应 相等,对应 相等,图形的 都没有发生变化,也就是旋转前后的两个图形为 .
(4)旋转作图的依据: 相等,对应点到旋转中心的 相等.旋转作图时,在确定了 后,依据指定的 和 画图,具体操作时往往通过 旋转后的位置,得到旋转后的图形.
4.中心对称
(1) 把一个图形绕着某一个点旋转 °,如果旋转后的图形能够与原来的图形 ,那么这个图形叫作 图形,这个点就是它的 .
(2)把一个图形绕着某一个点旋转 °, 如果它能够与另一个图形 ,那么就说这两个图形关于这个点成 ,这个点叫作 .这两个图形中的对应点叫作关于中心的 .
(3)关于中心对称的两个图形,对称点所连线段都经过 ,而且被对称中心所 .关于中心对称的两个图形是 图形.识别一个图形是否是中心对称图形,其依据是中心对称图形的定义,看其绕 后是否与其本身重合.若重合,则说明是中心对称图形;反之,则不是.
5.位似
(1)如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,像这样的两个图形叫作 ,这点叫作 ,也就是说这两个图形关于这点 ,它们的相似比又称 .
(2)位似图形上任意一对对应点到位似中心的距离之比等于 .
(3)在平面直角坐标系中,如果 是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的 比等于 或 .
实战演练
1.图中的图形为轴对称图形,该图形的对称轴的条数为 ( )
A.1 B.2
C.3 D.5
2.下列图形中既是轴对称图形又是中心对称图形的是 ( )
3.如图,将△ABC 折叠,使 AC 边落在 AB 边上,展开后得到折痕 l,则l 是△ABC的( )
A.中线 B.中位线
C.高线 D.角平分线
如图,△ABC与△DEF 位似,点O 是它们的位似中心,且相似比为 1 : 2,则△ABC 与△DEF 的周长
之比是 ( )
A.1:2
B.1:4
C.1:3
D.1:9
5.如图,在△ABC 中,AB=AC,若 M 是 BC 边上任意一 点, 将 △ABM 绕点A 逆时针旋转得到△ACN,点 M 的对应点为点 N,连接 MN,则下列结论一定正确的是 ( )
A. AB=AN
B. AB∥NC
C.∠AMN=∠ACN
D. MN⊥AC
6.如图,在△ABC中,∠ACB=90°,将△ABC绕点 C顺 时 针 旋 转 得 到△DEC,使点 B 的对应点 E 恰好落在边AC 上,点A 的对应点为D,延长 DE交AB 于点 F,则下列结论一定正确的是 ( )
A. AC=DE B. BC=EF
C.∠AEF=∠D D. AB⊥DF
7.如图,在平面直角坐标系中,△ABC 的顶点 A,B 的坐标分别是A(0,2),B(2,--1),平移△ABC 得到△A'B'C',若点 A 的对应点 A'的坐标为(--1,0),则 点 B 的 对 应 点 B' 的 坐 标是 .
8.如图, △ABC 中,点 D 为边 BC 的中点,连接AD,将△ADC 沿 直 线AD 翻 折 至 △ABC 所 在 平 面 内, 得△ADC',连接 CC',分别与边 AB 交于点E,与AD交于点O.若AE=BE,BC'=2,则AD的长为 .
9.如图,将周长为 8 的△ABC沿 BC 边向右平移2个单位,得到△DEF,则四边形 ABFD的周长为 .
10.如图,△ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将△ABC 平移后得到△A'B'C',且点 A的对应点是A'(2,3),点 B、C的对应点分别是 B'、C'.
(1)点 A、A'之间的距离是 ;
(2)请在图中画出△A'B'C'.
11.图1、图2 均是4×4 的正方形网格,每个小正方形的顶点称为格点.其中点 A,B,C均在格点上.请在给定的网格中按要求画四边形.
(1)在图1中,找一格点 D,使以点 A,B,C,D为顶点的四边形是轴对称图形.
(2)在图2中,找一格点 E,使以点 A,B,C,E为顶点的四边形是中心对称图形.
12.在矩形 ABCD 中,E 为DC 边上一点,把△ADE 沿AE 翻折,使点 D 恰好落在BC 边上的点 F.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4, 求 EC的长.
压轴预测
1.如图,在平面直角坐标系中,A(0,1),B(-1,0),C(1,0),请确定一点 D,使得以点 A,B,C,D为顶点的四边形是轴对称图形但不是中心对称图形,则点 D 的坐标可能是 ( )
A.(0,-1)
B.(2,1)
C.(0,-2)
D.(-1,1)
2.如图,在 Rt△ABC 中,∠B=90°,AB=12,AC=13.现将纸片进行折叠,使得顶点 B 落在AC 边上,对应点为 D,折痕为AE.则 BE的长为 ( )
A.2.4 B.2.5
C.2.8 D.3
3.如图是一张矩形纸片 ABCD,点 E 在AB边上,把△ADE 沿直线 DE 折叠,使点 A落在BC 边上的点 F 处.点 G 在 BC 边上,把△CDG沿直线 DG 折叠,使点 C 恰好落在 线 段 DF 上 的 点 H 处,∠EDG = °. 若 则
4.图1、图2均为7×6 的正方形网格,点 A,B,C在格点上.
(1)在图1中确定格点 D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形.(画一个即可)
(2)在图2中确定格点 E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形.(画一个即可)
5.在4×4的方格中,选择6个小方格涂上阴影,请仔细观察图1中的六个图案的对称性,按要求回答.
(1)请在六个图案中,选出三个具有相同对称性的图案.
选出的三个图案是 (填写序号);它们都是 图形(填写“中心对称”或“轴对称”);
(2)请在图2中,将1个小方格涂上阴影,使整个4×4的方格也具有(1)中所选图案相同的对称性.
6.如图,△ABC 的三个顶点坐标分别是A(0,3),B(1,0),C(3,1).
(1)以原点O 为位似中心,在y轴左侧画出△A B C ,使得△A B C 与△ABC 的位似比为2:1;
(2)△ABC 的内部一点 M 的坐标为(a,b),则点 M 在△A B C 中的对应点 M1的坐标是多少
7.如图,△ABC的三个顶点坐标分别为A(1,1),B(4,2),C(3,5).
(1)以O为旋转中心,将△ABC逆时针旋转90°得到△A B C ;
(2)将△ABC平移,使平移后点 B,C的对应点B2,C2分别在 y轴和x 轴上,画出平移后的△A B C ;
(3) 借助网格,利用无刻度直尺 画出△A B C 的中线C2D2.
参考答案
1.(1)沿某一方向 距离
(2)对应点 相等 平行(或在同一直线上)
(3)平移不改变图形的大小和形状 对应角相等 对应点所连的线段平行(或在同一直线上)且相等 方向 距离关键点 位置
2.(1)重合 轴对称图形 对称轴
(2)重合 轴对称 对称轴 对称点
(3)某直线 垂直平分线
3.(1)绕某一点O转动一个角度 点 O转动的角
(2)旋转中心 旋转方向 旋转角度旋转中心 方向 顺 逆 角度
(3)旋转中心 相同 距离 夹角 线段 形状与大小 全等图形
(4)旋转角 距离 旋转中心 旋转方向 旋转角度 几个关键点
4.(1)180 重合 中心对称 对称中心
(2)180 重合 中心对称 对称中心对称点
(3)对称中心 平分 全等 某一点旋转 180°
5.(1)位似图形 位似中心 位似 位似比
(2)位似比
(3)位似变换 k - k
1. D 【解析】本题考查轴对称图形的对称轴条数.如图,作出该图形的对称轴,其条数为5,故选 D.
2. B
3. D 【解析】本题考查轴对称的性质.由折叠知折痕平分∠BAC,故选 D.
4. A 【解析】本题考查位似的性质.△ABC 与△DEF 的周长之比与位似比相等,即为1:2,故选 A.
5. C
6. D 【解析】本题考查图形旋转的性质.由旋转的性质得AC= DC,BC=EC,∠A=∠D,又∠AEF=∠DEC,∴∠AFE=∠DCE=90°,∴AB⊥DF,∴一定正确的是D选项,故选 D.
7.(1,-3) 【解析】本题考查平移的性质.因为点 A 从(0,2)平移至 A'(-1,0),所以△ABC先向下平移2个单位长度,再向左平移1个单位长度,所以点 B(2,-1)平移后的对应点 B'的坐标为(1,-3).
8.3 【解析】本题考查翻折的性质、三角形的中位线定理、全等三角形的判定与性质.由翻折的性质可知△DCA≌△DC'A,OC=OC',∠COD=∠C'OD=90°,所以 O为CC'的中点.因为 D为BC 的中点,所以OD 是△BCC'的中位线,所以OD= BC',OD∥BC',所以∠COD= 因为 AE=BE,BC'=2,所以OD=1.在△EC' B 和 △EOA 中, 所 以△EC'B≌△EOA(AAS),所以. 所以 AO=2,所以AD=AO+OD=2+1=3.
9.12 【解析】本题考查图形的平移.∵平移的距离为 2个单位长度,∴AD=CF=2.又∵AC=DF,∴四边形ABFD的周长为8+2+2=12.
10.(1)4 (2)图略
解:(1)4.
(2)如图,△A'B'C'即为所求作.
11.(1)略 (2)略
(1)以AC为对称轴,作点 B的对称点 D,则四边形 ABCD即为所求;或以 BC的垂直平分线为对称轴,作点 A 的对称点 D,则四边形 ABCD 即为所求;或以 AC的垂直平分线为对称轴,作点 B的对称点D,则四边形ABCD即为所求;(2)以AC为对角线或以AC 为边作平行四边形即可.
解:答案不唯一,以下答案供参考:
评分说明:(1)未标注点 D,E或标注错误,但所画图形正确不扣分.
(2)作图痕迹是虚线不扣分.
(3)点的位置正确但没画四边形共扣1分.
(4)第(1)问和第(2)问只画对一个给3分.
12.(1)略
(1)根据两角对应相等的两个三角形相似即可证明;
(2)设CE=x,由 △ABF∽△FCE,可得 ∠CFE =∠BAF=30°,进而得EF=2x,由此即可求解.
解:(1)由题意得∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°.
又∵∠EFC+∠FEC=90°,
∴∠AFB=∠FEC.
又∵∠B=∠C,
∴△ABF∽△FCE.
∴AF=4且∠BAF=30°.
又∵△ABF∽△FCE,
∴∠CFE=∠BAF=30°.
设CE=x,
则EF=2x,
压轴预测
1. C 【解析】本题考查中心对称图形和轴对称图形.分别在坐标系中描出选项中的各点,观察所得的图形,可知点(0,-2)与A,B,C三点构成的四边形是轴对称图形但不是中心对称图形,故选 C.
2. A 【解析】本题考查折叠的性质、勾股定理的应用.∵∠B=90°,AC=13,AB=12,∴BC=√AC -AB =5.设BE=x.由折叠的性质,可得AD=AB=12,DE=BE=x,∠ADE=∠B=90°,∴CD=AC-AD=13-12=1,EC=BC-BE=5-x.在 Rt△DEC中, DE ,即( 解得x=2.4,∴BE=2.4,故选 A.
3.45 【解析】本题考查矩形的性质、轴对称的性质、锐角三角函数.在矩形 ABCD 中,∠ADC=90°,由折叠
可知,∠ADE=∠EDH,∠HDG=∠GDC,∴∠EDH+ 即∠EDG=45°;∵BF+CG= 即
4.(1)略 (2)略
解:(1)画出符合要求的图形如下.(答案不唯一)
(2)画出符合要求的图形如下.(答案不唯一)
5.(1)①③⑤ 轴对称(或②④⑥ 中心对称) (2)略
解:(1)①③⑤轴对称(或②④⑥ 中心对称)
(2)轴对称
中心对称
6.(1)略 (2)(-2a,-2b)
(1)依据位似中心及位似比的大小即可作出△A B C ;
(2)根据位似比和位似图形的位置即可求解.
解:(1)如图所示,△A B C 即为所求.
(2)∵△A B C 与△ABC 的位似比为2 :1,△A B C 在 y轴左侧,△ABC的内部一点M 的坐标为(a,b),
则点 M 在 △A B C 中 的 对 应 点 M 的 坐 标是(-2a,-2b).
7.略
解:(1)如图.
(2)如图.
(3)如图.
同课章节目录
