专题9几何图形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习
文档属性
| 名称 | 专题9几何图形 知识点梳理及专项练习(含解析)--2025年中考数学一轮复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 494.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题9几何图形
1.经过两点有一条 ,并且只有一条直线.简单说成: .
2.两点的所有连线中, .简单说成: .
3.两点的距离:连接两点间的线段的 ,叫作这两点的距离.
4.(1)∠1和∠2有一条公共边OC,它们具有这种关系的两个角,互为 .
(2)∠1 和∠3有一个公共顶点 O,并且∠1的两边分别是∠3的 ,具有这种关系的两个角,互为 .
5.两条直线互相垂直,其中一条直线叫作另一条直线的 ,它们的交点叫作 .
6.连接直线外一点与直线上各点的所有线段中, .
7. “三线八角”的识别:三线八角指的是两条直线被 所截而成的 个角.正确认 识这八个角要 抓 住:同位角 相同,即“同旁”和“同规”;内错角要抓住“内部, ”;同旁内角要抓住“内部, ”.
8.平行线的判定方法
(1) ,两直线平行;(2) ,两直线平行;(3) ,两直线平行.
9.平行线的性质
(1)两直线平行, ;(2)两直线平 行, ; (3) 两直 线 平行, .
10.一般地,用光线照射物体,在地面上或墙壁上得到的 叫作物体的投影.投影可以分为平行投影、正投影、中心投影.由 (如太阳光线)形成的投影称为平行投影;由 发出的光线所形成的投影称为中心投影;投影线 于投影面产生的投影叫作正投影.在实际制图中,人们经常采用正投影.
11.当我们从某一角度观察一个实物时,所看到的图象叫作物体的一个 .物体的三视图特指主视图、俯视图、左视图.在 内得到的由前向后观察物体的视图,叫作主视图;在水平面内 得到 的由 观察物体的视图,叫作俯视图;在侧面内得到的 观察物体的视图,叫作左视图,有时也叫作侧视图.
12.视图的性质:三视图中,主视图与俯视图表示同一物体的 ,主视图与左视图表示同一物体的 ,左视图与俯视图表示同一物体的 ,因此三个视图的大小是互相联系的.画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的 对正,主视图与左视图的 对齐,左视图与俯视图的 相等.这些要求可以概括为十五个字“主俯长对正,俯左宽相等,左主高平齐”.
13.有些立体图形是由一些平面图形围成的,将它们的表面适当 ,可以展开成 ,这样的平面图形称为相应立体图形的 .
14.一个几何体能展开成一个平面图形,这个平面图形就可以 成相应的几何体, 与 是一个互逆过程.
15.用无刻度的 和 作图,这就是尺规作图.
实战演练
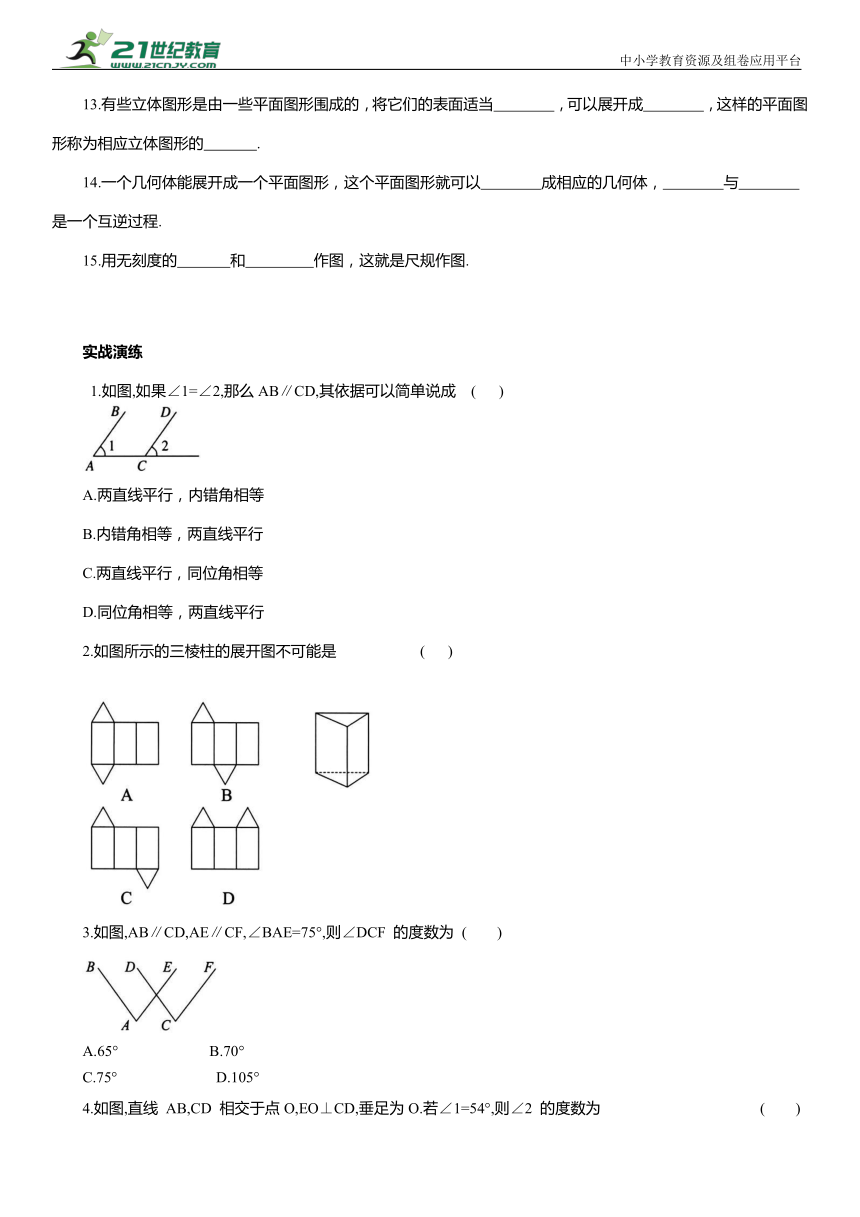
1.如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成 ( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
2.如图所示的三棱柱的展开图不可能是 ( )
3.如图,AB∥CD,AE∥CF,∠BAE=75°,则∠DCF 的度数为 ( )
A.65° B.70°
C.75° D.105°
4.如图,直线 AB,CD 相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2 的度数为 ( )
A.26° B.36°
C.44° D.54°
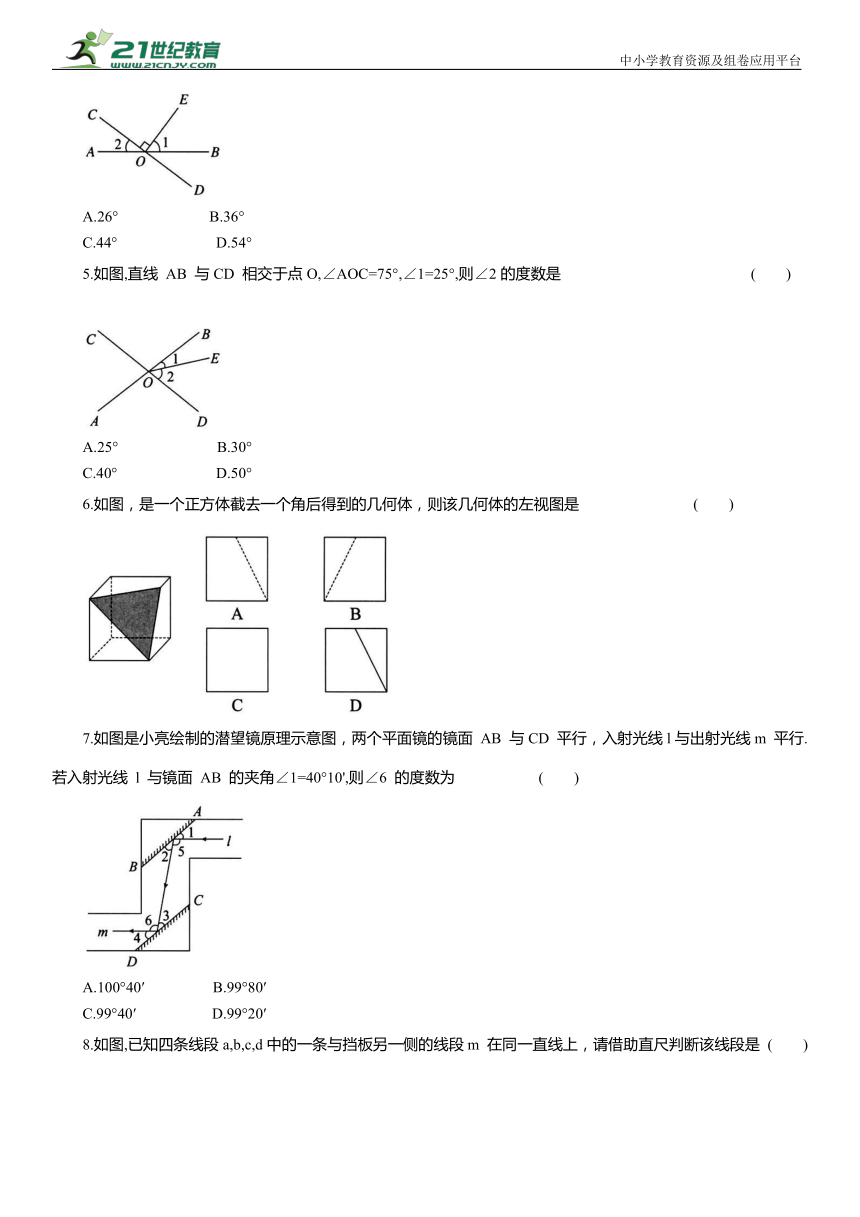
5.如图,直线 AB 与CD 相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是 ( )
A.25° B.30°
C.40° D.50°
6.如图,是一个正方体截去一个角后得到的几何体,则该几何体的左视图是 ( )
7.如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面 AB 与CD 平行,入射光线l与出射光线m 平行.若入射光线 l 与镜面 AB 的夹角∠1=40°10',则∠6 的度数为 ( )
A.100°40′ B.99°80′
C.99°40′ D.99°20′
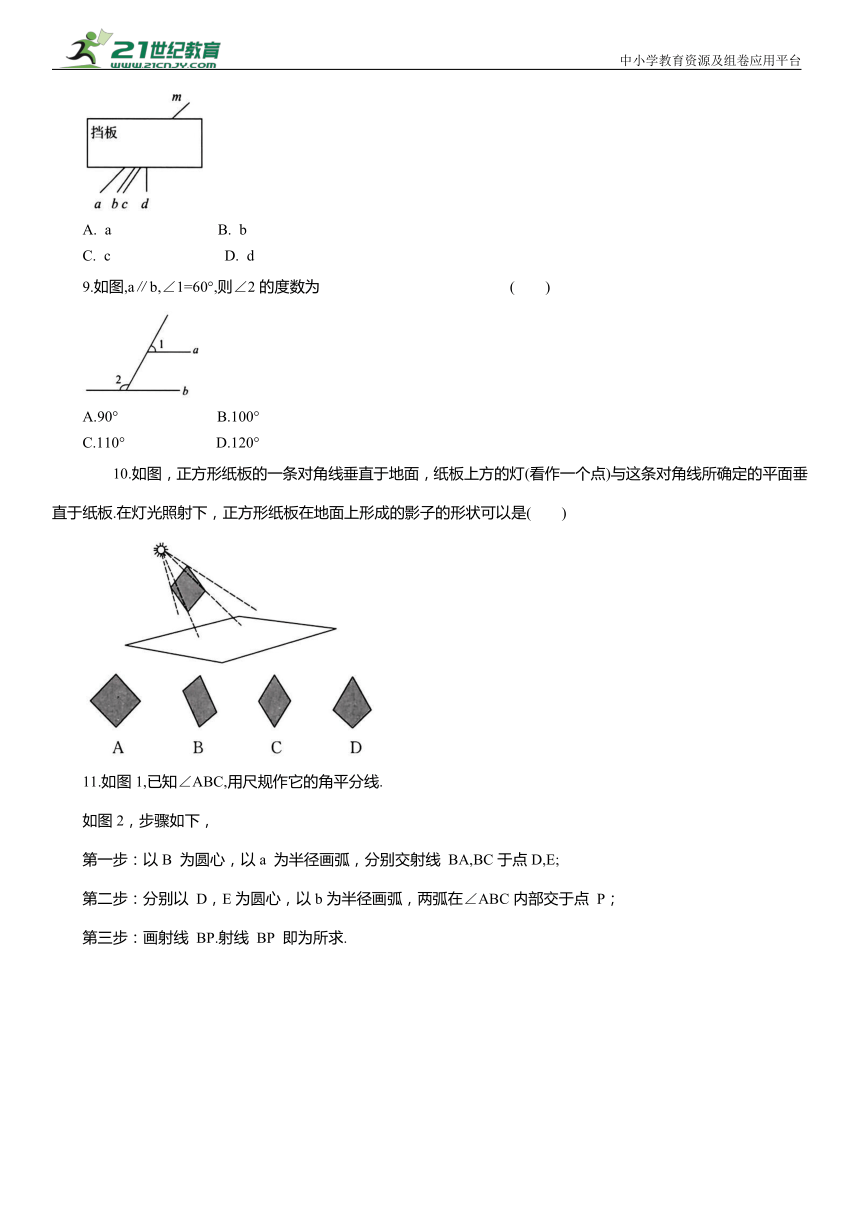
8.如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m 在同一直线上,请借助直尺判断该线段是 ( )
A. a B. b
C. c D. d
9.如图,a∥b,∠1=60°,则∠2的度数为 ( )
A.90° B.100°
C.110° D.120°
10.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
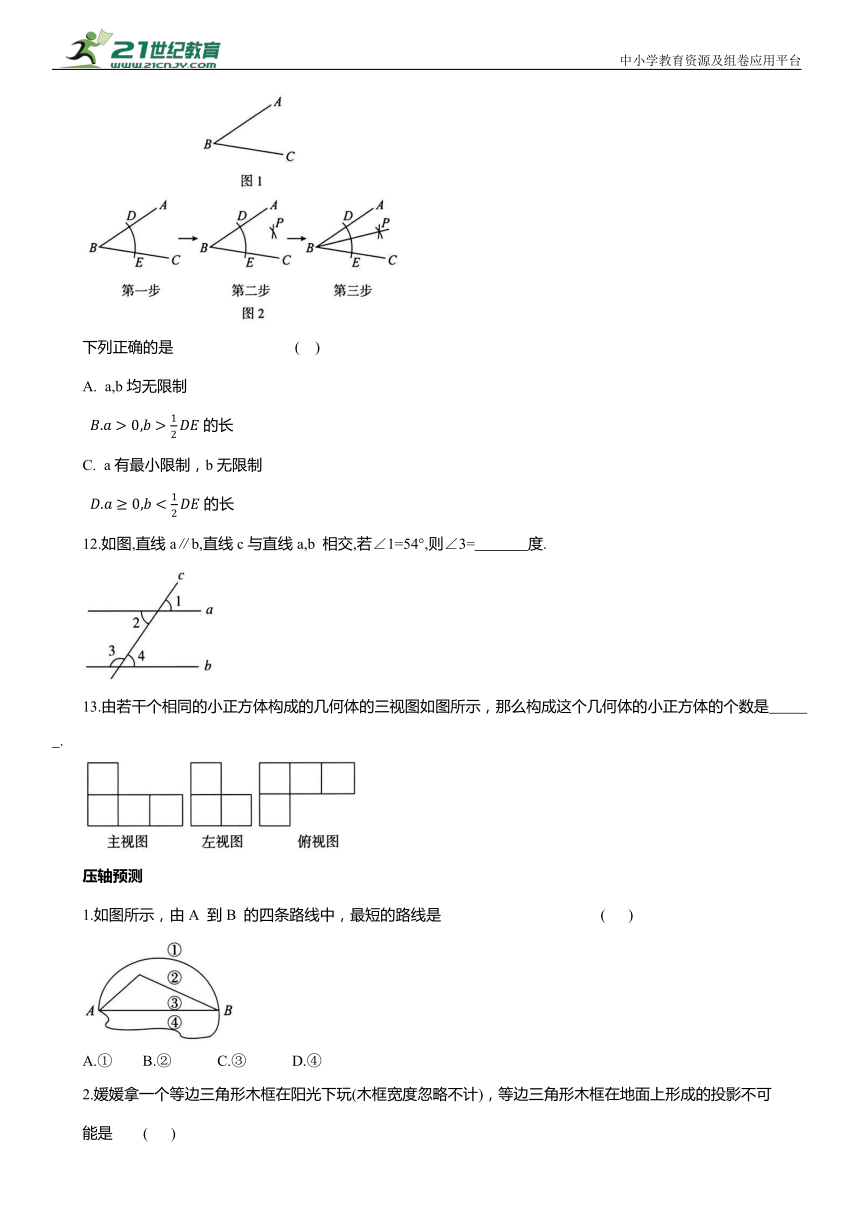
11.如图1,已知∠ABC,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以B 为圆心,以a 为半径画弧,分别交射线 BA,BC于点D,E;
第二步:分别以 D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点 P;
第三步:画射线 BP.射线 BP 即为所求.
下列正确的是 ( )
A. a,b均无限制
的长
C. a有最小限制,b无限制
的长
12.如图,直线a∥b,直线c与直线a,b 相交,若∠1=54°,则∠3= 度.
13.由若干个相同的小正方体构成的几何体的三视图如图所示,那么构成这个几何体的小正方体的个数是 .
压轴预测
1.如图所示,由A 到B 的四条路线中,最短的路线是 ( )
A.① B.② C.③ D.④
2.媛媛拿一个等边三角形木框在阳光下玩(木框宽度忽略不计),等边三角形木框在地面上形成的投影不可
能是 ( )
3.用“垂线段最短”来解释的现象是 ( )
4.如图的展开图中,能围成三棱柱的是 ( )
5.把一副三角尺放在同一水平桌面上,如果它们的两个直角顶点重合,两条斜边平行(如图所示),那么∠1的度数是 ( )
A.75° B.90° C.100° D.105°
6.如图,四个几何体中,主视图是矩形的有( )
A.4个 B.3个 C.2个 D.1个
7.如图是一款手推车的平面示意图,其中AB∥CD,∠3=150°,∠1=30°,则∠2 的大小是 ( )
A.60° B.70° C.80° D.90°
8.如图,由作图痕迹做出如下判断,其中正确的是 ( )
A. FH>HG B. FH=HG
C. EF>FH D. EF=FH
9.如图,AD 平分∠BAC,点 E 在 AB 上,EF∥AC交AD 于点G,若∠DGF=40°,则∠BEF的度数为 ( )
A.20° B.40°
C.50° D.80°
10.如图,有一条直的等宽纸带,按图折叠时形成一个 30°的角,则重叠部分的∠α等于 ( )
A.85° B.75°
C.65° D.60°
11.如图,AB∥CD,∠CED=90°,∠AEC=37°,则∠D 的度数为 .
12. 如 图, 在 Rt △ABC 中, ∠C = 90°,AC动手操作:要求尺规作图,不写作法,但保留作图痕迹.
①作出 AB 的垂直平分线 MN,MN 分别与AB 交于点D,与 BC交于点 E.
②过点 B 作 BF 垂直于AE,垂足为 F.
参考答案
1.直线 两点确定一条直线
2.线段最短 两点之间,线段最短
3.长度
4.(1)反向延长线 邻补角
(2)反向延长线对顶角
5.垂线 垂足
6.垂线段最短
7.第三条直线 八 位置 两旁 同旁
8.(1)同位角相等
(2)内错角相等
(3)同旁内角互补
9.(1)同位角相等
(2)内错角相等
(3)同旁内角互补
10.影子 一组平行光线 某一点 垂直
11.视图 正面 上向下 由左向右
12.长 高 宽 长 高 宽
13.剪开 平面图形 展开图
14.折叠 展开 折叠
15.直尺 圆规
1. D 【解析】本题考查平行线的判定.由图可知,∠1 和∠2的位置关系是同位角,则由∠1=∠2判定AB∥CD,其依据是同位角相等,两直线平行,故选 D.
2. D 【解析】本题考查三棱柱的展开图.三棱柱的展开图同一侧不能有两个三角形,所以三棱柱的展开图不可能是选项D中的图形,故选 D.
3. C 【解析】本题考查平行线的性质.如图,AE与CD 交于点O.因为AB∥CD,所以∠DOE=∠BAE=75°.因为AE∥CF,所以∠DCF=∠DOE=75°,故选 C.
4. B 【解析】本题考查平角的性质.∵EO⊥CD,∴∠EOC= 故选 B.
5. D 【解 析】本 题 考 查 对 顶 角. ∵ ∠AOC = 75°,∴∠BOD=75°.又∵∠1=25°,∴∠2=∠BOD-∠1= 故选 D.
6. A 【解析】本题考查几何体的左视图.根据已知几何体,从左边看得到的图形是故选 A.
7. C 【解析】本题考查反射的性质、平行线的性质、平角的定义.由题知, .因为 AB∥CD,所以∠3=∠2=40°10′,所以∠4=∠3=40°10′,所以∠6= ,故选 C.
8. A 【解析】本题考查直线的定义.利用直尺画出图形,可以看出线段a与m在一条直线上,故选 A.
9. D 【解析】本题考查平行线的性质、邻补角的定义.如图,∵a∥b,∴∠3=∠1=60°,∴∠2=180°-60°=120°,故选 D.
10. D 【解析】本题考查中心投影.中心投影的物高和影长成正比,∵正方形的对角线互相垂直,∴形成的影子的对角线也互相垂直.又∵灯与对角线所确定的平面与纸板垂直,∴形成的影子有一个角是直角,∴形成的影子是,故选 D.
11. B 【解析】本题考查尺规作图.第一步:以点 B为圆心,适当长为半径画弧,分别交射线 BA,BC 于点 D,E,∴a>0;第二步:分别以点 D,E为圆心,大于 DE的长为半径画弧,两弧在∠ABC内部交于点P, 的长;第三步:画射线 BP,射线 BP 即为所求.综上,答案为 的长,故选 B.
掌握作角平分线的方法是解决问题的关键.
12.126 【解析】本题考查平行线的性质、平角的定义.因为a∥b,所以∠4=∠1=54°,所以.
由对顶角相等得∠2=∠1=54°.因为a∥b,所以∠2+∠3=180°,所以.
13.5 【解析】本题考查由三视图还原几何体.由俯视图可知,该几何体的最底层有四个小正方体,又根据主视图和左视图可知,左上角有一个小正方体,∴一共有5个小正方体.
压轴预测
1. C 【解析】本题考查最短距离.∵两点之间线段最短,∴由A 到B 的四条路线中,最短的路线是③,故选 C.
2. B 【解析】本题考查图形的投影.当等边三角形木框与阳光平行时,投影是一条直线,故选项 A 正确;当等边三角形木框与阳光垂直时,投影是一个等边三角形,故选项C正确;当等边三角形木框与阳光有一定角度时,投影是一个等腰三角形,故选项D正确;但无论如何投影都不能得到一个点,故选项 B错误,故选 B.
3. A 【解析】本题考查点到直线的距离、直线的性质、线段的性质. A选项利用了垂线段最短;B,C选项利用了两点确定一条直线;D选项利用了两点之间线段最短,故选 A.
4. D 【解析】本题考查几何体的展开图.逐项分析如表,
选项 逐项分析 正误
A 展开图经过折叠后能围成四棱锥 ×
B 展开图经过折叠后能围成圆柱 ×
C 展开图经过折叠后能围成圆锥 ×
D 展开图经过折叠后能围成三棱柱 √
故选 D.
5. D 【解析】本题考查平行线的性质、三角板中的特殊角.如图,设三角尺的两直角顶点交于点 M,过点 M作EF∥AB.∵AB∥CD∥EF,∴∠A=∠AME,∠C=∠CME.又∠A=45°,∠C=60°,∴∠1=∠AME+∠CME= ,即∠1 的度数是 105°,故选 D.
6. B 【解析】本题考查几何体的三视图.由图可知,圆柱的主视图是矩形,圆锥的主视图是三角形,直三棱柱的主视图是矩形,长方体的主视图是矩形,∴主视图是矩形的几何体有3个,故选 B.
7. A 【解析】本题考查平行线的性质、补角的概念.如图,过点 E 作EF∥AB,则∠OEF=∠AOE=180°-∠3=30°.因为AB∥CD,所以 EF∥CD,所以∠DEF=∠1=30°,所以∠2=∠OEF+∠DEF=60°,故选 A.
8. A 【解析】本题考查尺规作图、角平分线的性质.由作图
痕迹可知PC为∠APB的平分线,DE为线段PQ 的垂直平分线,根据角平分线上的点到角的两边的距离相等,得FH>HG,而 EF与FH 的关系不能确定,故选 A.
9. D 【解析】本题考查平行线的性质、角平分线的定义.∵EF∥AC,∠DGF=40°,∴∠DAC=∠DGF=40°,∠BEF = ∠BAC. ∵ AD 平分∠BAC,∴∠BEF =∠BAC=2∠DAC=80°,故选 D.
10. B 【解析】本题考查图形翻折变换.∵纸带的两边互相平行,∴∠2=30°.又由翻折变换的性质可知,∠1= 故选 B.
11. 53°【解 析】本 题 考 查 平 角、平行 线 的 性 质.∵∠CED=90°,∠AEC=37°,∴∠BED=180°-90°-37°=53°.∵AB∥CD,∴∠D=∠BED=53°.
12.略
根据要求进行尺规作图.
解:①②如图,直线 MN,BF就是所求作的直线.
专题9几何图形
1.经过两点有一条 ,并且只有一条直线.简单说成: .
2.两点的所有连线中, .简单说成: .
3.两点的距离:连接两点间的线段的 ,叫作这两点的距离.
4.(1)∠1和∠2有一条公共边OC,它们具有这种关系的两个角,互为 .
(2)∠1 和∠3有一个公共顶点 O,并且∠1的两边分别是∠3的 ,具有这种关系的两个角,互为 .
5.两条直线互相垂直,其中一条直线叫作另一条直线的 ,它们的交点叫作 .
6.连接直线外一点与直线上各点的所有线段中, .
7. “三线八角”的识别:三线八角指的是两条直线被 所截而成的 个角.正确认 识这八个角要 抓 住:同位角 相同,即“同旁”和“同规”;内错角要抓住“内部, ”;同旁内角要抓住“内部, ”.
8.平行线的判定方法
(1) ,两直线平行;(2) ,两直线平行;(3) ,两直线平行.
9.平行线的性质
(1)两直线平行, ;(2)两直线平 行, ; (3) 两直 线 平行, .
10.一般地,用光线照射物体,在地面上或墙壁上得到的 叫作物体的投影.投影可以分为平行投影、正投影、中心投影.由 (如太阳光线)形成的投影称为平行投影;由 发出的光线所形成的投影称为中心投影;投影线 于投影面产生的投影叫作正投影.在实际制图中,人们经常采用正投影.
11.当我们从某一角度观察一个实物时,所看到的图象叫作物体的一个 .物体的三视图特指主视图、俯视图、左视图.在 内得到的由前向后观察物体的视图,叫作主视图;在水平面内 得到 的由 观察物体的视图,叫作俯视图;在侧面内得到的 观察物体的视图,叫作左视图,有时也叫作侧视图.
12.视图的性质:三视图中,主视图与俯视图表示同一物体的 ,主视图与左视图表示同一物体的 ,左视图与俯视图表示同一物体的 ,因此三个视图的大小是互相联系的.画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的 对正,主视图与左视图的 对齐,左视图与俯视图的 相等.这些要求可以概括为十五个字“主俯长对正,俯左宽相等,左主高平齐”.
13.有些立体图形是由一些平面图形围成的,将它们的表面适当 ,可以展开成 ,这样的平面图形称为相应立体图形的 .
14.一个几何体能展开成一个平面图形,这个平面图形就可以 成相应的几何体, 与 是一个互逆过程.
15.用无刻度的 和 作图,这就是尺规作图.
实战演练
1.如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成 ( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
2.如图所示的三棱柱的展开图不可能是 ( )
3.如图,AB∥CD,AE∥CF,∠BAE=75°,则∠DCF 的度数为 ( )
A.65° B.70°
C.75° D.105°
4.如图,直线 AB,CD 相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2 的度数为 ( )
A.26° B.36°
C.44° D.54°
5.如图,直线 AB 与CD 相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是 ( )
A.25° B.30°
C.40° D.50°
6.如图,是一个正方体截去一个角后得到的几何体,则该几何体的左视图是 ( )
7.如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面 AB 与CD 平行,入射光线l与出射光线m 平行.若入射光线 l 与镜面 AB 的夹角∠1=40°10',则∠6 的度数为 ( )
A.100°40′ B.99°80′
C.99°40′ D.99°20′
8.如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m 在同一直线上,请借助直尺判断该线段是 ( )
A. a B. b
C. c D. d
9.如图,a∥b,∠1=60°,则∠2的度数为 ( )
A.90° B.100°
C.110° D.120°
10.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
11.如图1,已知∠ABC,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以B 为圆心,以a 为半径画弧,分别交射线 BA,BC于点D,E;
第二步:分别以 D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点 P;
第三步:画射线 BP.射线 BP 即为所求.
下列正确的是 ( )
A. a,b均无限制
的长
C. a有最小限制,b无限制
的长
12.如图,直线a∥b,直线c与直线a,b 相交,若∠1=54°,则∠3= 度.
13.由若干个相同的小正方体构成的几何体的三视图如图所示,那么构成这个几何体的小正方体的个数是 .
压轴预测
1.如图所示,由A 到B 的四条路线中,最短的路线是 ( )
A.① B.② C.③ D.④
2.媛媛拿一个等边三角形木框在阳光下玩(木框宽度忽略不计),等边三角形木框在地面上形成的投影不可
能是 ( )
3.用“垂线段最短”来解释的现象是 ( )
4.如图的展开图中,能围成三棱柱的是 ( )
5.把一副三角尺放在同一水平桌面上,如果它们的两个直角顶点重合,两条斜边平行(如图所示),那么∠1的度数是 ( )
A.75° B.90° C.100° D.105°
6.如图,四个几何体中,主视图是矩形的有( )
A.4个 B.3个 C.2个 D.1个
7.如图是一款手推车的平面示意图,其中AB∥CD,∠3=150°,∠1=30°,则∠2 的大小是 ( )
A.60° B.70° C.80° D.90°
8.如图,由作图痕迹做出如下判断,其中正确的是 ( )
A. FH>HG B. FH=HG
C. EF>FH D. EF=FH
9.如图,AD 平分∠BAC,点 E 在 AB 上,EF∥AC交AD 于点G,若∠DGF=40°,则∠BEF的度数为 ( )
A.20° B.40°
C.50° D.80°
10.如图,有一条直的等宽纸带,按图折叠时形成一个 30°的角,则重叠部分的∠α等于 ( )
A.85° B.75°
C.65° D.60°
11.如图,AB∥CD,∠CED=90°,∠AEC=37°,则∠D 的度数为 .
12. 如 图, 在 Rt △ABC 中, ∠C = 90°,AC
①作出 AB 的垂直平分线 MN,MN 分别与AB 交于点D,与 BC交于点 E.
②过点 B 作 BF 垂直于AE,垂足为 F.
参考答案
1.直线 两点确定一条直线
2.线段最短 两点之间,线段最短
3.长度
4.(1)反向延长线 邻补角
(2)反向延长线对顶角
5.垂线 垂足
6.垂线段最短
7.第三条直线 八 位置 两旁 同旁
8.(1)同位角相等
(2)内错角相等
(3)同旁内角互补
9.(1)同位角相等
(2)内错角相等
(3)同旁内角互补
10.影子 一组平行光线 某一点 垂直
11.视图 正面 上向下 由左向右
12.长 高 宽 长 高 宽
13.剪开 平面图形 展开图
14.折叠 展开 折叠
15.直尺 圆规
1. D 【解析】本题考查平行线的判定.由图可知,∠1 和∠2的位置关系是同位角,则由∠1=∠2判定AB∥CD,其依据是同位角相等,两直线平行,故选 D.
2. D 【解析】本题考查三棱柱的展开图.三棱柱的展开图同一侧不能有两个三角形,所以三棱柱的展开图不可能是选项D中的图形,故选 D.
3. C 【解析】本题考查平行线的性质.如图,AE与CD 交于点O.因为AB∥CD,所以∠DOE=∠BAE=75°.因为AE∥CF,所以∠DCF=∠DOE=75°,故选 C.
4. B 【解析】本题考查平角的性质.∵EO⊥CD,∴∠EOC= 故选 B.
5. D 【解 析】本 题 考 查 对 顶 角. ∵ ∠AOC = 75°,∴∠BOD=75°.又∵∠1=25°,∴∠2=∠BOD-∠1= 故选 D.
6. A 【解析】本题考查几何体的左视图.根据已知几何体,从左边看得到的图形是故选 A.
7. C 【解析】本题考查反射的性质、平行线的性质、平角的定义.由题知, .因为 AB∥CD,所以∠3=∠2=40°10′,所以∠4=∠3=40°10′,所以∠6= ,故选 C.
8. A 【解析】本题考查直线的定义.利用直尺画出图形,可以看出线段a与m在一条直线上,故选 A.
9. D 【解析】本题考查平行线的性质、邻补角的定义.如图,∵a∥b,∴∠3=∠1=60°,∴∠2=180°-60°=120°,故选 D.
10. D 【解析】本题考查中心投影.中心投影的物高和影长成正比,∵正方形的对角线互相垂直,∴形成的影子的对角线也互相垂直.又∵灯与对角线所确定的平面与纸板垂直,∴形成的影子有一个角是直角,∴形成的影子是,故选 D.
11. B 【解析】本题考查尺规作图.第一步:以点 B为圆心,适当长为半径画弧,分别交射线 BA,BC 于点 D,E,∴a>0;第二步:分别以点 D,E为圆心,大于 DE的长为半径画弧,两弧在∠ABC内部交于点P, 的长;第三步:画射线 BP,射线 BP 即为所求.综上,答案为 的长,故选 B.
掌握作角平分线的方法是解决问题的关键.
12.126 【解析】本题考查平行线的性质、平角的定义.因为a∥b,所以∠4=∠1=54°,所以.
由对顶角相等得∠2=∠1=54°.因为a∥b,所以∠2+∠3=180°,所以.
13.5 【解析】本题考查由三视图还原几何体.由俯视图可知,该几何体的最底层有四个小正方体,又根据主视图和左视图可知,左上角有一个小正方体,∴一共有5个小正方体.
压轴预测
1. C 【解析】本题考查最短距离.∵两点之间线段最短,∴由A 到B 的四条路线中,最短的路线是③,故选 C.
2. B 【解析】本题考查图形的投影.当等边三角形木框与阳光平行时,投影是一条直线,故选项 A 正确;当等边三角形木框与阳光垂直时,投影是一个等边三角形,故选项C正确;当等边三角形木框与阳光有一定角度时,投影是一个等腰三角形,故选项D正确;但无论如何投影都不能得到一个点,故选项 B错误,故选 B.
3. A 【解析】本题考查点到直线的距离、直线的性质、线段的性质. A选项利用了垂线段最短;B,C选项利用了两点确定一条直线;D选项利用了两点之间线段最短,故选 A.
4. D 【解析】本题考查几何体的展开图.逐项分析如表,
选项 逐项分析 正误
A 展开图经过折叠后能围成四棱锥 ×
B 展开图经过折叠后能围成圆柱 ×
C 展开图经过折叠后能围成圆锥 ×
D 展开图经过折叠后能围成三棱柱 √
故选 D.
5. D 【解析】本题考查平行线的性质、三角板中的特殊角.如图,设三角尺的两直角顶点交于点 M,过点 M作EF∥AB.∵AB∥CD∥EF,∴∠A=∠AME,∠C=∠CME.又∠A=45°,∠C=60°,∴∠1=∠AME+∠CME= ,即∠1 的度数是 105°,故选 D.
6. B 【解析】本题考查几何体的三视图.由图可知,圆柱的主视图是矩形,圆锥的主视图是三角形,直三棱柱的主视图是矩形,长方体的主视图是矩形,∴主视图是矩形的几何体有3个,故选 B.
7. A 【解析】本题考查平行线的性质、补角的概念.如图,过点 E 作EF∥AB,则∠OEF=∠AOE=180°-∠3=30°.因为AB∥CD,所以 EF∥CD,所以∠DEF=∠1=30°,所以∠2=∠OEF+∠DEF=60°,故选 A.
8. A 【解析】本题考查尺规作图、角平分线的性质.由作图
痕迹可知PC为∠APB的平分线,DE为线段PQ 的垂直平分线,根据角平分线上的点到角的两边的距离相等,得FH>HG,而 EF与FH 的关系不能确定,故选 A.
9. D 【解析】本题考查平行线的性质、角平分线的定义.∵EF∥AC,∠DGF=40°,∴∠DAC=∠DGF=40°,∠BEF = ∠BAC. ∵ AD 平分∠BAC,∴∠BEF =∠BAC=2∠DAC=80°,故选 D.
10. B 【解析】本题考查图形翻折变换.∵纸带的两边互相平行,∴∠2=30°.又由翻折变换的性质可知,∠1= 故选 B.
11. 53°【解 析】本 题 考 查 平 角、平行 线 的 性 质.∵∠CED=90°,∠AEC=37°,∴∠BED=180°-90°-37°=53°.∵AB∥CD,∴∠D=∠BED=53°.
12.略
根据要求进行尺规作图.
解:①②如图,直线 MN,BF就是所求作的直线.
同课章节目录
