2025高考物理二轮专题复习-第10讲 热学计算题型突破 课件 (共43张PPT)

(共43张PPT)
第10讲 热学计算题型突破
角度1 密闭汽缸类问题
角度2 液柱类问题
角度3 理想气体变质量问题
角度4 关联气体问题
跟踪训练
备用习题
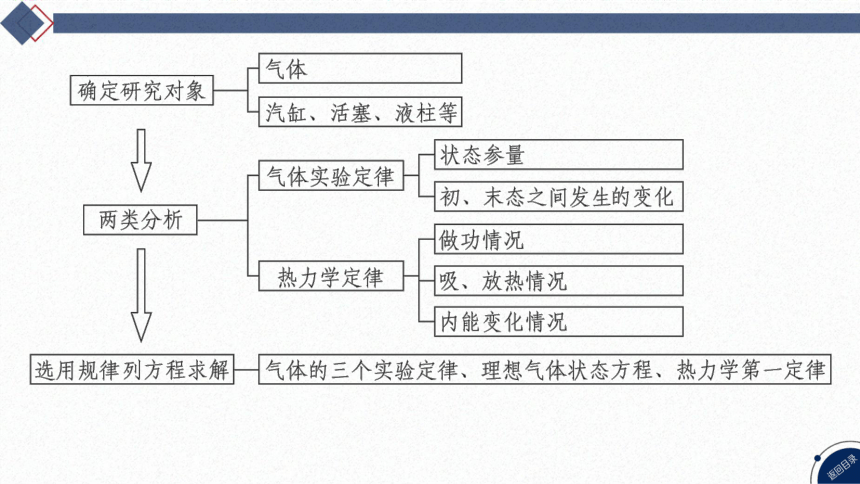
解答此类问题的方法是：找出不同状态下的三个状态参量，分析理想气体
发生的是何种变化，利用理想气体的状态方程列方程求解；要能用力学观
点分析各处压强的关系，要注意研究过程中哪些量不变，哪些量变化，选
择合适的气体实验定律解决问题.
解气体实验定律与热力学定律的综合问题的一般思路
角度1 密闭汽缸类问题
例1 [2024·丽水模拟] 如图甲所示，一导热性能良好、内壁光滑的汽缸水
平放置，横截面积、质量 、厚度不计的活塞与汽
缸底部之间封闭了一部分理想气体，此时活塞与汽缸底部之间的距离
，在活塞的右侧 处有一对与汽缸固定连接的卡环，
气体的温度，大气压强 .现将
汽缸竖直放置，如图乙所示，取 .
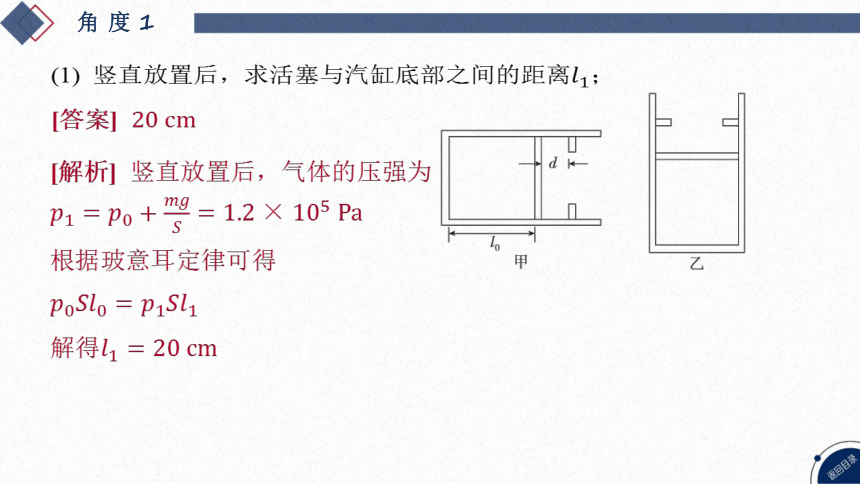
(1) 竖直放置后，求活塞与汽缸底部之间的距离 ；
[答案]
[解析] 竖直放置后，气体的压强为
根据玻意耳定律可得
解得
[解析] 假设 时活塞到达卡环处，则有
根据理想气体状态方程可得
解得
符合假设，则气体的压强为
(2) 竖直放置后，求加热到时气体的压强 ；
[答案]
[解析] 根据热力学第一定律得
活塞到达卡环前气体压强不变，到达卡环后不做功，则有
联立可得
(3) 若汽缸竖直放置时气体压强为，加热到时的压强为 ，活塞移
动距离为，气体总共吸收热量为，求气体内能的增加量 (选用以下物
理量表示：、、、、、、 ).
[答案]
技法点拨
气体先做等温压缩，再升温，具体过程如下：
(1)竖直过程中气体发生等温变化，根据玻意耳定律判断气体的体积变化;
(2)加热过程中气体先发生等压变化，再发生等容变化，根据理想气体状
态方程求气体在时的压强;
(3)根据热力学第一定律结合吸放热、做功情况，求气体内能增加量.
角度2 液柱类问题
例2 [2024·山东卷] 图甲为战国时期青铜汲酒器，根据其原理制作了由中
空圆柱形长柄和储液罐组成的汲液器，如图乙所示.长柄顶部封闭，横截
面积,长度，侧壁有一小孔 .储液罐的横截面积
、高度，罐底有一小孔 .汲液时，将汲液器竖
直浸入液体，液体从孔进入，空气由孔 排出；当内外液面相平时，长
柄浸入液面部分的长度为；堵住孔 ，缓慢地将汲液器竖直提出液面，
储液罐内刚好储满液体.已知液体密度 ，重力加速度
大小取，大气压 .整个过程温度保持不变，空气
可视为理想气体，忽略器壁厚度.
[解析] 在缓慢地将汲液器竖直提出液面的过程中，封闭气体发生等温变
化，根据玻意耳定律有
根据题意可知，
联立解得
(1) 求 ;
[答案]
[解析] 对新进入的气体和原有的气体整体分析，由玻意耳定律有
又
联立解得
(2) 松开孔，从外界进入压强为、体积为 的空气，使满储液罐中液体
缓缓流出，堵住孔，稳定后罐中恰好剩余一半的液体，求 .
[答案]
技法点拨
本题考查液柱关联气体问题，一般由活塞、液柱相联系的“两团气”问题,要注
意寻找“两团气”之间的压强、体积或长度关系,列出辅助方程,最后联立求解.
角度3 理想气体变质量问题
1.在“充气、抽气”模型中可以把充进或抽出的气体包含在气体变化的始、
末状态中,即用等效法把变质量问题转化为恒定质量的问题.
2.分装问题和漏气问题
(1)分装问题
将一个大容器里的气体分装到多个小容器中的问题,可以把大容器中的气
体和多个小容器中的气体整体作为研究对象,将变质量问题转化为恒定质
量问题.
(2)漏气问题
容器漏气过程中气体的质量不断发生变化,不能用理想气体状态方程求解.
如果选容器内原有气体为研究对象,便可使变质量问题变成质量一定的气
体状态变化的问题,可用理想气体状态方程求解.
例3 [2024·金华一中月考] 自行车在生活中是一种普
及程度很高的交通工具.自行车轮胎气压过低不仅费
力而且很容易损坏内胎，轮胎气压过高会使轮胎的
缓冲性能下降或发生爆胎，因此保持合适的轮胎气
压对延长轮胎使用寿命和提升骑行感受至关重要.已知某款自行车轮胎容
积为且保持不变，在环境温度为 条件下，胎内气体压强为
，外界大气压强为 .
[解析] 气体做等容变化，有
得
(1) 若该车长时间骑行在温度较高的公路上使胎内气体的温度上升到 ，
求此时车内气体的压强.
[答案]
(2) 若车胎的气门芯会缓慢漏气，长时间放置后胎内压强变为
，忽略气体温度与车胎容积的变化，求胎内泄漏出的气
体质量占原来胎内气体质量的比例.
[答案]
[解析] 原胎内气体做等温膨胀，有
得
故
即有三分之一的气体泄漏.
(3) 若自行车说明书规定的轮胎标准气压在室温 下为
，为使车胎内气压达标，某同学用打气筒给自行车打气.
设每打一次可打入压强为、温度为的空气 .请
通过计算判断打气10次后车胎压强是否达到说明书规定的标准胎压.假设
打气过程气体的温度保持不变，车胎因膨胀而增大的体积可以忽略不计.
[答案] 未达标准胎压
[解析] 设原胎内气体做等温膨胀后压强变为 时体
积变为 ，得
再将胎内气体和打气筒打入的气体看作整体一起做
等温压缩，有，
联立解得
故胎内气体未达标准气压.
技法点拨
热学变质量问题经常就是充气、漏气、放气现象,或者容器气体分装等现
象.常用的就是通过假设的方法,将需要充入的气体或者是放出的气体的体
积设出来,放到一个袋子里,与容器连接成一体，即用等效法把变质量问题
转化为恒定质量的问题,再用理想气体状态方程求解.
角度4 关联气体问题
这类问题涉及两部分气体，它们之间虽然没有气体交换，但其压强或体积
这些量间有一定的关系，建立这两部分气体的压强关系和体积关系是解决
问题的关键.
例4 如图，一个盛有气体的容器内壁光滑，被隔板分
成、 两部分，隔板绝热.开始时系统处于平衡状
态，和体积均为、压强均为大气压 、温度均为
环境温度.现将接一个打气筒，打气筒每次打气都把压强为 、温度为
、体积为的气体打入中. 缓慢打气若干次后，的体积变为
(所有气体均视为理想气体).
(1) 假设打气过程中整个系统温度保持不变，求打气的次数 ；
[答案] 10次
[解析] 对 中气体，根据玻意耳定律得
解得
对 内原气体和充入的气体，根据玻意耳定律得
解得
(2) 保持中气体温度不变，加热中气体使的体积恢复为，求 中气体
的温度 .
[答案]
[解析] 中气体温度不变，根据玻意耳定律得
解得
对 中气体，根据理想气体状态方程得
解得
技法点拨
解决关联气体问题的一般方法
(1)分别选取每部分气体为研究对象，确定初、末状态参量，根据气体状
态方程列式.
(2)认真分析两部分气体的压强、体积之间的关系，并列出方程.
(3)多个方程联立求解.
1.　如图所示,导热良好的固定直立圆筒内用面积S=100 cm2、质量m=1 kg的活塞封闭一定质量的理想气体,活塞能无摩擦滑动.圆筒与温度300 K的热源接触,平衡时圆筒内气体处于状态A,其体积VA=600 cm3.缓慢推动活塞使气体达到状态B,此时体积VB=500 cm3.固定活塞,升高热源温度,气体达到状态C,此时压强pC=1.4×105 Pa.已知从状态A到状态C,气体从外界吸收热量Q=14 J;从状态B到状态C,气体内能增加ΔU=25 J;大气压p0=1.01×105 Pa.
(1)气体从状态A到状态B,其分子平均动能　　　　(选填“增大”“减小”或“不变”),圆筒内壁单位面积受到的压力　　　　(选填“增大”“减小”或“不变”);
不变
增大
[解析] 气体从状态A到状态B,由于圆筒导热良好,缓慢推动活塞时,气体做等温变化,而温度是分子平均动能大小的标志,因此分子平均动能不变;气体温度不变,体积减小,由=C可知,压强增大,即圆筒内壁单位面积受到的压力增大.
(2)求气体在状态C的温度TC;
[答案] 350 K　
[解析] 气体在状态A时,对活塞受力分析可得,封闭气体压强为pA=p0-=105 Pa
从状态A到C,由理想气体状态方程可得
代入数值得TC=350 K.
(3)求气体从状态A到状态B过程中外界对系统做的功W.
[答案] 11 J
[解析] 气体从状态A到状态B时,外界对气体做功W,内能不变,从状态B到C时,体积不变,没有做功,即气体吸收热量25 J,内能增加25 J.因此从A到C整个过程中,根据热力学第一定律有ΔU=W+Q,代入数值得W=11 J.
2.　如图所示,竖直放置、导热性能良好的U形玻璃管截面均匀,左端开口、右端封闭,左、右管内用长度分别为h1=5 cm、h2=10 cm的水银柱封闭两段理想气体a、b.气体a的长度La=15 cm,气体b的长度Lb=20 cm,最初环境温度T1=300 K时,两水银柱下表面齐平.现缓慢升高环境温度,直至两段水银柱的上表面齐平.已知大气压强为75 cmHg,右侧水银柱未进入U形玻璃管的水平部分,两段气体均可视为理想气体.求:
(1)两段水银柱的下表面齐平时气体b的压强;
[答案] 70 cmHg　
[解析] 设大气压强为p0,对气体a,有pa=p0+ρgh1
对气体b,有pb=pa-ρgh2
联立两式,代入数据得pb=70 cmHg
[解析] 升温过程中气体b发生等压变化,则温度升高
体积增大,设右侧水银柱下降x cm,变化前后对比如图所示
对气体a有Va=(La-x+h2-h1-x)S
对气体b,由盖-吕萨克定律得,解得
缓慢升高环境温度过程中气体a也发生等压变化,
由盖-吕萨克定律得
联立解得T2= K=327.3 K
(2)两段水银柱的上表面齐平时环境的温度T2.
[答案] 327.3 K
3.　现代瓷器可采用电热窑炉烧制,电热窑炉不需要燃烧设备,窑内制品不受烟气及灰渣等影响,温度便于实现精确控制.若初始时窑炉内温度为27 ℃,压强为大气压强p0,已知某瓷器的烧制温度约为1227 ℃.
(1)窑炉不排气的情况下,求达到烧制温度时窑炉内的气体压强;
[答案] 5p0　
[解析] 初始压强为p0,温度为T0=(273+27) K
达到烧制温度时,压强为p1,温度为T1=(273+1227) K
根据查理定律有
解得p1=5p0
(2)若窑炉内压强要控制在2.8p0~3p0之间,求达到烧制温度后排出气体质量与初始时窑炉内气体总质量的比值η的范围.
[答案] ≥η≥
[解析] 设初始时气体体积为V0,达到烧制温度且压强为2.8p0时,排出的气体较多
根据理想气体状态方程有
解得V1=V0
排出的气体质量与初始时总质量的比值为η1=
达到烧制温度且压强为3p0时,根据理想气体状态方程有
解得V2=V0
排出的气体质量与初始时总质量的比值为η2=则达到烧制温度后排出气体质量与初始时窑炉内气体总质量的比值的范围为≥η≥
1.[2023·广东卷] 在驻波声场作用下,水中小气泡
周围液体的压强会发生周期性变化,使小气泡周
期性膨胀和收缩，气泡内气体可视为质量不变
的理想气体，其膨胀和收缩过程可简化为如图
所示的图像,气泡内气体先从压强为 、体
积为、温度为的状态 等温膨胀到体积为
、压强为的状态.然后从状态 绝热收缩
到体积为、压强为、温度为的状态, 状态到状态 过程中外界
对气体做功为.已知、、和 .求:
(1) 的表达式;
[答案]
[解析] 从状态到状态 ,气体发生等温变化,根据玻意定律有
,解得 .
(2) 的表达式；
[答案]
[解析] 从状态到状态，由理想气体状态方程 ,
又 ,解
得 .
(3) 状态到状态 过程，气泡内气体的内能变化.
[答案]
[解析] 状态到状态 为绝热过程,由热力学第一定律
知,气体的内能变化为 .
2.如图所示的装置中,三支内径相等的玻璃管、 和
用细管连通.、两管上端等高,管上端封闭, 管
上端与大气相通,管内装有水银且、 两管内的水
银面等高,管中的活塞可滑动且密封良好.、和
竖直且整个装置平衡,、 管中的空气柱长度均为
,管中的水银柱足够长.现在将 管中的活塞缓
慢向上推,直到管中的水银上升到管口. 管中封闭
的气体可视为理想气体,活塞移动过程中整个装置的温度保持不变.已知大
气压强 ,求:
(1) 管中的水银上升到管口时, 管中气体的压强;
[答案]
[解析] 因为开始时、管中的空气柱长度相等,所以 管中
气体的压强
设管中的水银上升到管口时,管中空气柱的长度为 ,玻璃
管的横截面积为，此时管中气体的压强
由玻意耳定律得
解得,
(2) 整个过程 管中的活塞向上移动的距离.
[答案]
[解析] 管中水银柱上升的高度
管中水银柱上升的高度
、管中增加的水银都来源于管,又三管内径相等,所以
管中活塞上升的距离等于、 管的水银柱上升的高度之和,
所以管活塞向上移动的距离
解得