2024-2025学年北师大版数学八年级上册期末冲刺试卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学八年级上册期末冲刺试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 11:31:31 | ||
图片预览



文档简介
2024-2025学年北师大版数学八年级上册期末冲刺试卷
姓名:___________班级:___________学号:___________
一、单选题
1.在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.使式子有意义的的取值范围是( )
A. B. C. D.
3.下列说法中,正确的是( )
A.的立方根是 B.的立方根是
C.的立方根是 D.没有立方根
4.下列是关于的函数,其中是一次函数的为( )
A. B. C. D.
5.一直角三角形的两直角边长为6和8,则斜边长为( )
A.5 B.13 C.10 D.14
6.已知关于x、y的二元一次方程组的解互为相反数,则k的值是( )
A.0 B.-1 C.1 D.2
7.因疫情原因,学校采取了“停课不停学”的措施老师们可以通过网上直播的方式进行教学,也可以进行网上听课等活动某校上周进行了网上公开课竞赛,数学组组长统计了本组每个老师上周听网上公开课的节数,得到了如下表则下列说法不正确的是( )
听课的节数 2 3 4 5 6
人数 2 2 6 4 1
A.数学组老师共有15人 B.每人听课节数的众数是4
C.每人听课节数的中位数是6 D.每人听课节数的平均数是4
8.某工厂现有105名工人,一名工人每天可生产8个螺杆或26个螺母,2个螺母和1个螺杆为一套,现在要求工人每天生产的螺杆和螺母完整配套没有剩余,若设安排x名工人生产螺杆,y名工人生产螺母,则列出正确的二元一次方程组为( )
A. B.
C. D.
9.实数a,b,c在数轴上的对应点如图,化简的值是( )
A. B.c-b C. D.
10.《郑州市优化生育政策促进人口长期均衡发展实施办法》于2023年9月1日全面启动实施,明确规定对新生儿入户郑州市的一孩、二孩、三孩及以上家庭发放不同金额的育儿补贴,有利于减小新生儿家庭的育儿压力.婴儿车是新生儿家庭必买的单品,如图是某畅销婴儿车的平面示意图,其中,,,那么的度数为( )
A. B. C. D.
11.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头所示方向,每次移动1个单位,依次得到点,…,根据这个规律,点的坐标为( )
A. B. C. D.
12.“激情马拉松·活力好青年”,2023年12月10日,诸暨西施马拉松鸣笛开跑.在比赛过程中,乙选手匀速跑完全程,甲选手后的速度为,甲、乙两选手的部分行程随起跑的时间变化的图象如图所示,下列说法中正确的个数有( )
①起跑后半小时内甲的速度为;②第1小时两人都跑了;
③图中记录的两人所跑路程都为;④图中所示的截止行程点处乙比甲早到.
A.1个 B.2个 C.3个 D.4个
二、填空题
13.的结果是 .
14.写出一个解为的二元一次方程组: .
15.某同学6次引体向上的测试成绩(单位:个)分别为16、18、20、17、16、18,这组数据的中位数是 .
16.已知一个圆的半径为,一矩形的长为,若该圆的面积与矩形的面积相等, 则矩形的宽为 .
17.若点A、B:(﹣2,y1)、(﹣1,y2)都在直线y=kx+b上,且直线y=kx+b和直线y=﹣2x+5平行,则y1 y2(填>,<,=).
18.已知 是方程 (为常数) 的解,则的值为 .
19.《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何,意思是:一根竿子横放,竿比门宽长出四尺;竖放,竿比门高长出二尺,斜放恰好能出去,则竿长是 尺.
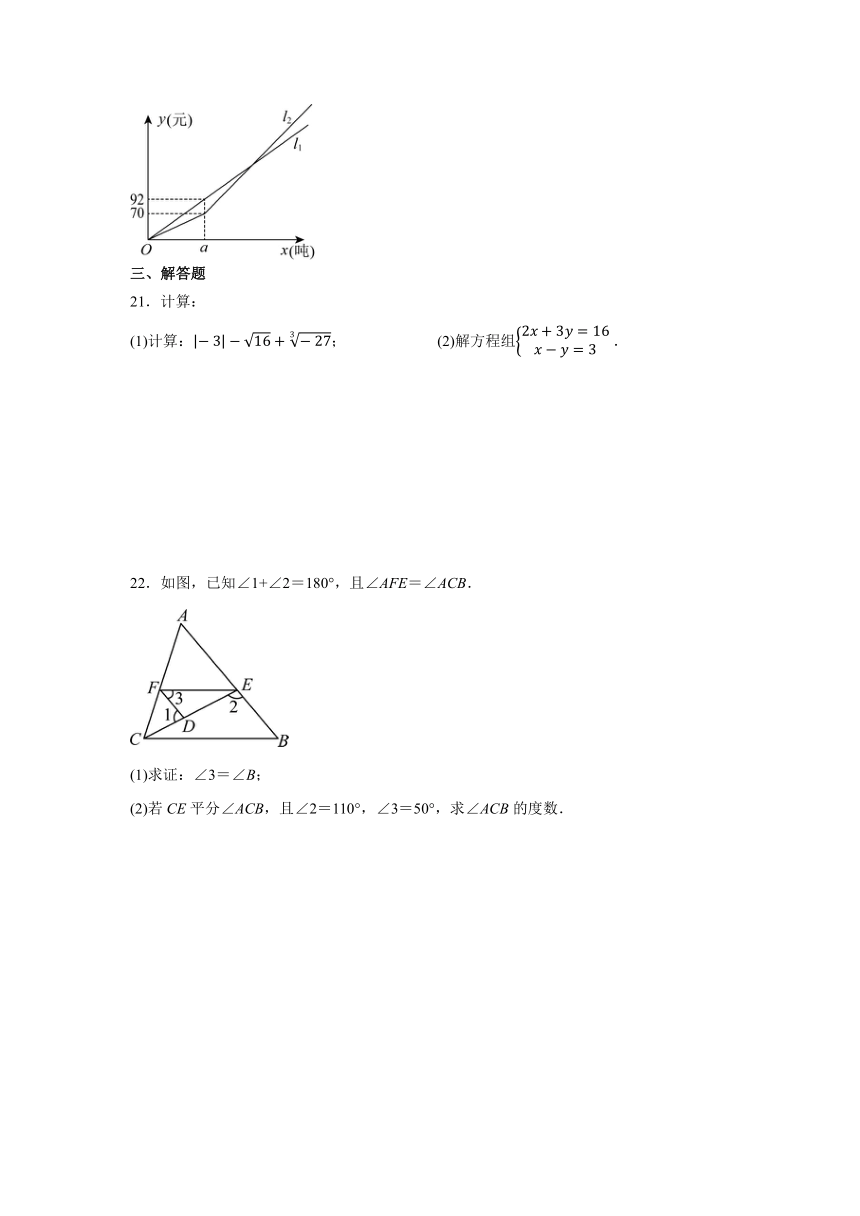
20.某市去年居民用水按照元吨收取费用,为提倡居民节约用水,自今年月日起对居民用水实行阶梯水费,规定:若用水超过吨,超过吨的部分每吨增加元.图中,分别表示去年、今年水费(元)与用水量(吨)之间的关系.实行阶梯水费后,若用水超过吨,则超过吨的部分每吨水费为 元.
三、解答题
21.计算:
(1)计算:; (2)解方程组.
22.如图,已知∠1+∠2=180°,且∠AFE=∠ACB.
(1)求证:∠3=∠B;
(2)若CE平分∠ACB,且∠2=110°,∠3=50°,求∠ACB的度数.
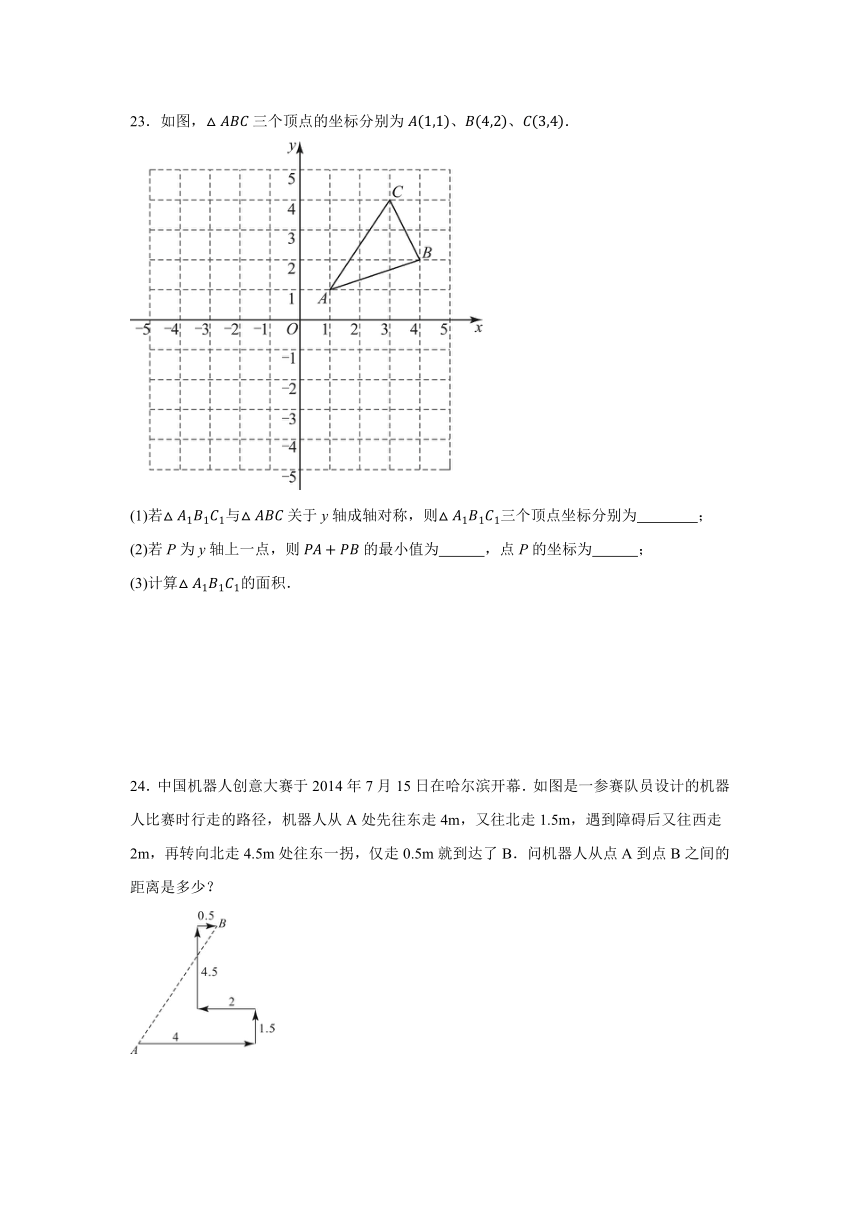
23.如图,三个顶点的坐标分别为、、.
(1)若与关于y轴成轴对称,则三个顶点坐标分别为 ;
(2)若P为y轴上一点,则的最小值为 ,点P的坐标为 ;
(3)计算的面积.
24.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
25.某中学在七、八年级举行了“奥运会运知识竞赛”活动,现从七、八年级各随机抽取50名学生的竞赛成绩,整理如下:(得分用表示,共分成四组::;:;:;:):八年级50名学生成绩数据中,落在组中的成绩分别是:91,94,94,93,92,91,93,94,91,90,94,91,94,92,92.
根据以上信息,解答下列问题:
七、八年级抽取的学生竞赛成绩统计表
班级 平均数 中位数 众数
七年级 91 92 95
八年级 91 96
(1)直接写出上述图表中、的值:__________,___________;
(2)根据以上数据分析,你认为七、八年级哪个年级竞赛成绩较好?请说明理由.
(3)该校八年级共1200人参加了此次竞赛,请估计参加此次竞赛成绩为优秀的八年级学生有多少人?
26.已知用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
27.某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C;甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.
(1)乙步行的速度为 米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙相遇?(请直接写出答案).
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C C B C C B D
题号 11 12
答案 A C
1. D
2. B
3. C
4. C
5. C
6. B
7. C
8. C
9. B
10. D
11.A
12.C
13.
14.答案不唯一,如
15.17.5
16.
17.>
18.
19.10
20.
21.(1)解:
;
(2)
得:,
解得:,
将代入②得:,
解得:,
原方程组的解为.
22.(1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∴,
∴∠3=∠AEF,
∵∠AFE=∠ACB,
∴,
∴∠AEF=∠B,
∴∠B=∠3;
(2)解:∵∠3=∠B,∠3=50°,
∴∠B=50°,
∵∠2+∠B+∠ECB=180°,∠2=110°,
∴∠ECB=20°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=40°.
23.(1)解:作图如下,
由图形知,,,,
(2)如图,
连接交y轴于点P,
∵与关于y轴成轴对称,
,
,
根据两点之间线段最短得到:的长就是的最小值,
∵,,
∴,
设直线的解析式为:,
根据,,
可得:,
解得:,
即直线的解析式为:,
当时,,
∴,
(3)为:
.
24.过点B作BCAD于C,
所以AC=4﹣2+0.5=2.5m,BC=4.5+1.5=6m,
在直角△ABC中,AB为斜边,则m,
答:机器人从点A到点B之间的距离是m.
25.(1)解:八年级C组占比为,
∴八年级D组占比:,
∴.
八年级50名学生成绩数据中,A、B组人数为,
中位数是第25、26个数据(按照成绩从低到高排列),落在C组,
将C组中的成绩重新排列为:90,91,91,91,91,92,92,93,93,93,94,94,94,94,94.
∴中位数;
(2)解:八年级成绩较好,理由如下
从中位数看,八年级的中位数高于七年级的中位数;从众数看,八年级的众数高于七年级的众数.
∴八年级成绩较好;
(3)解:(人).
答:估计参加此次比赛成绩优秀()的八年级学生人数是人
26.(1)解:设每辆A型车、B型车都载满货物一次可以分别运货x吨、y吨,
依题意,得
解得
答:1辆A型车载满货物一次可运3吨,1辆B型车载满货物一次可运4吨
(2)解:由(1),得,
∴.
∵a,b都是正整数,
∴或或
∴有3种租车方案:
方案一:A型车9辆,B型车1辆;
方案二:A型车5辆,B型车4辆;
方案三:A型车1辆,B型车7辆.
(3)解:∵A型车每辆需租金100元/次,B型车每辆需租金120元/次,
∴方案一需租金:(元);
方案二需租金:(元);
方案三需租金:(元).
∵,
∴最省钱的租车方案是方案三:A型车1辆,B型车7辆.
答:租A型车1辆,B型车7辆,最少租车费为940元.
27.(1)解:乙步行的速度为:
(米/分),
(2)设乙乘景区观光车时与之间的函数关系式为 ,
将代入得:
解得:
∴乙乘景区观光车时与之间的函数关系式为;
(3)甲步行的速度为:(米/分),
∴甲步行与之间的函数关系式为
当时,联立两函数关系式成方程组
解得:
∴甲出发分钟与乙第一次相遇;
当时,,解得,
∴甲出发分钟与乙第二次相遇;
当时,,解得:,
∴甲出发分钟与乙第三次相遇;
综上所述,甲出发分钟、分钟或分钟与乙相遇.
姓名:___________班级:___________学号:___________
一、单选题
1.在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.使式子有意义的的取值范围是( )
A. B. C. D.
3.下列说法中,正确的是( )
A.的立方根是 B.的立方根是
C.的立方根是 D.没有立方根
4.下列是关于的函数,其中是一次函数的为( )
A. B. C. D.
5.一直角三角形的两直角边长为6和8,则斜边长为( )
A.5 B.13 C.10 D.14
6.已知关于x、y的二元一次方程组的解互为相反数,则k的值是( )
A.0 B.-1 C.1 D.2
7.因疫情原因,学校采取了“停课不停学”的措施老师们可以通过网上直播的方式进行教学,也可以进行网上听课等活动某校上周进行了网上公开课竞赛,数学组组长统计了本组每个老师上周听网上公开课的节数,得到了如下表则下列说法不正确的是( )
听课的节数 2 3 4 5 6
人数 2 2 6 4 1
A.数学组老师共有15人 B.每人听课节数的众数是4
C.每人听课节数的中位数是6 D.每人听课节数的平均数是4
8.某工厂现有105名工人,一名工人每天可生产8个螺杆或26个螺母,2个螺母和1个螺杆为一套,现在要求工人每天生产的螺杆和螺母完整配套没有剩余,若设安排x名工人生产螺杆,y名工人生产螺母,则列出正确的二元一次方程组为( )
A. B.
C. D.
9.实数a,b,c在数轴上的对应点如图,化简的值是( )
A. B.c-b C. D.
10.《郑州市优化生育政策促进人口长期均衡发展实施办法》于2023年9月1日全面启动实施,明确规定对新生儿入户郑州市的一孩、二孩、三孩及以上家庭发放不同金额的育儿补贴,有利于减小新生儿家庭的育儿压力.婴儿车是新生儿家庭必买的单品,如图是某畅销婴儿车的平面示意图,其中,,,那么的度数为( )
A. B. C. D.
11.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头所示方向,每次移动1个单位,依次得到点,…,根据这个规律,点的坐标为( )
A. B. C. D.
12.“激情马拉松·活力好青年”,2023年12月10日,诸暨西施马拉松鸣笛开跑.在比赛过程中,乙选手匀速跑完全程,甲选手后的速度为,甲、乙两选手的部分行程随起跑的时间变化的图象如图所示,下列说法中正确的个数有( )
①起跑后半小时内甲的速度为;②第1小时两人都跑了;
③图中记录的两人所跑路程都为;④图中所示的截止行程点处乙比甲早到.
A.1个 B.2个 C.3个 D.4个
二、填空题
13.的结果是 .
14.写出一个解为的二元一次方程组: .
15.某同学6次引体向上的测试成绩(单位:个)分别为16、18、20、17、16、18,这组数据的中位数是 .
16.已知一个圆的半径为,一矩形的长为,若该圆的面积与矩形的面积相等, 则矩形的宽为 .
17.若点A、B:(﹣2,y1)、(﹣1,y2)都在直线y=kx+b上,且直线y=kx+b和直线y=﹣2x+5平行,则y1 y2(填>,<,=).
18.已知 是方程 (为常数) 的解,则的值为 .
19.《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何,意思是:一根竿子横放,竿比门宽长出四尺;竖放,竿比门高长出二尺,斜放恰好能出去,则竿长是 尺.
20.某市去年居民用水按照元吨收取费用,为提倡居民节约用水,自今年月日起对居民用水实行阶梯水费,规定:若用水超过吨,超过吨的部分每吨增加元.图中,分别表示去年、今年水费(元)与用水量(吨)之间的关系.实行阶梯水费后,若用水超过吨,则超过吨的部分每吨水费为 元.
三、解答题
21.计算:
(1)计算:; (2)解方程组.
22.如图,已知∠1+∠2=180°,且∠AFE=∠ACB.
(1)求证:∠3=∠B;
(2)若CE平分∠ACB,且∠2=110°,∠3=50°,求∠ACB的度数.
23.如图,三个顶点的坐标分别为、、.
(1)若与关于y轴成轴对称,则三个顶点坐标分别为 ;
(2)若P为y轴上一点,则的最小值为 ,点P的坐标为 ;
(3)计算的面积.
24.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
25.某中学在七、八年级举行了“奥运会运知识竞赛”活动,现从七、八年级各随机抽取50名学生的竞赛成绩,整理如下:(得分用表示,共分成四组::;:;:;:):八年级50名学生成绩数据中,落在组中的成绩分别是:91,94,94,93,92,91,93,94,91,90,94,91,94,92,92.
根据以上信息,解答下列问题:
七、八年级抽取的学生竞赛成绩统计表
班级 平均数 中位数 众数
七年级 91 92 95
八年级 91 96
(1)直接写出上述图表中、的值:__________,___________;
(2)根据以上数据分析,你认为七、八年级哪个年级竞赛成绩较好?请说明理由.
(3)该校八年级共1200人参加了此次竞赛,请估计参加此次竞赛成绩为优秀的八年级学生有多少人?
26.已知用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
27.某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C;甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.
(1)乙步行的速度为 米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙相遇?(请直接写出答案).
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C C B C C B D
题号 11 12
答案 A C
1. D
2. B
3. C
4. C
5. C
6. B
7. C
8. C
9. B
10. D
11.A
12.C
13.
14.答案不唯一,如
15.17.5
16.
17.>
18.
19.10
20.
21.(1)解:
;
(2)
得:,
解得:,
将代入②得:,
解得:,
原方程组的解为.
22.(1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∴,
∴∠3=∠AEF,
∵∠AFE=∠ACB,
∴,
∴∠AEF=∠B,
∴∠B=∠3;
(2)解:∵∠3=∠B,∠3=50°,
∴∠B=50°,
∵∠2+∠B+∠ECB=180°,∠2=110°,
∴∠ECB=20°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=40°.
23.(1)解:作图如下,
由图形知,,,,
(2)如图,
连接交y轴于点P,
∵与关于y轴成轴对称,
,
,
根据两点之间线段最短得到:的长就是的最小值,
∵,,
∴,
设直线的解析式为:,
根据,,
可得:,
解得:,
即直线的解析式为:,
当时,,
∴,
(3)为:
.
24.过点B作BCAD于C,
所以AC=4﹣2+0.5=2.5m,BC=4.5+1.5=6m,
在直角△ABC中,AB为斜边,则m,
答:机器人从点A到点B之间的距离是m.
25.(1)解:八年级C组占比为,
∴八年级D组占比:,
∴.
八年级50名学生成绩数据中,A、B组人数为,
中位数是第25、26个数据(按照成绩从低到高排列),落在C组,
将C组中的成绩重新排列为:90,91,91,91,91,92,92,93,93,93,94,94,94,94,94.
∴中位数;
(2)解:八年级成绩较好,理由如下
从中位数看,八年级的中位数高于七年级的中位数;从众数看,八年级的众数高于七年级的众数.
∴八年级成绩较好;
(3)解:(人).
答:估计参加此次比赛成绩优秀()的八年级学生人数是人
26.(1)解:设每辆A型车、B型车都载满货物一次可以分别运货x吨、y吨,
依题意,得
解得
答:1辆A型车载满货物一次可运3吨,1辆B型车载满货物一次可运4吨
(2)解:由(1),得,
∴.
∵a,b都是正整数,
∴或或
∴有3种租车方案:
方案一:A型车9辆,B型车1辆;
方案二:A型车5辆,B型车4辆;
方案三:A型车1辆,B型车7辆.
(3)解:∵A型车每辆需租金100元/次,B型车每辆需租金120元/次,
∴方案一需租金:(元);
方案二需租金:(元);
方案三需租金:(元).
∵,
∴最省钱的租车方案是方案三:A型车1辆,B型车7辆.
答:租A型车1辆,B型车7辆,最少租车费为940元.
27.(1)解:乙步行的速度为:
(米/分),
(2)设乙乘景区观光车时与之间的函数关系式为 ,
将代入得:
解得:
∴乙乘景区观光车时与之间的函数关系式为;
(3)甲步行的速度为:(米/分),
∴甲步行与之间的函数关系式为
当时,联立两函数关系式成方程组
解得:
∴甲出发分钟与乙第一次相遇;
当时,,解得,
∴甲出发分钟与乙第二次相遇;
当时,,解得:,
∴甲出发分钟与乙第三次相遇;
综上所述,甲出发分钟、分钟或分钟与乙相遇.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
