2024-2025学年北师大版数学九年级上册期末冲刺试卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学九年级上册期末冲刺试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 407.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 11:32:44 | ||
图片预览



文档简介
2024-2025学年北师大版数学九年级上册期末冲刺试卷
姓名:___________班级:___________学号:___________
一、单选题
1.如图所示的立体图形,其主视图是( )
A. B. C. D.
2.对于反比例函数,下列结论错误的是( )
A.函数图象分布在第一、三象限
B.函数图象经过点
C.若点在其图象上,那么点也一定在其图象上
D.若点都在函数图象上,且,则
3.如图是超市的两个摇奖转盘,只有当两个转盘指针同时指在偶数上时才能获一等奖,则摇奖人中一等奖的概率是( )
A. B. C. D.
4.如图,与是位似图形,是位似中心,位似比为,若,则的长为( )
A. B. C. D.
5.将x2+6x+4=0进行配方变形,下列正确的是( )
A.(x+3)2=5 B.(x+3)2=9 C.(x+6)2=32 D.(x+6)2=9
6.若关于的一元二次方程有两个不相等的实数根,则的取值范围为( )
A.且 B.且
C. D.
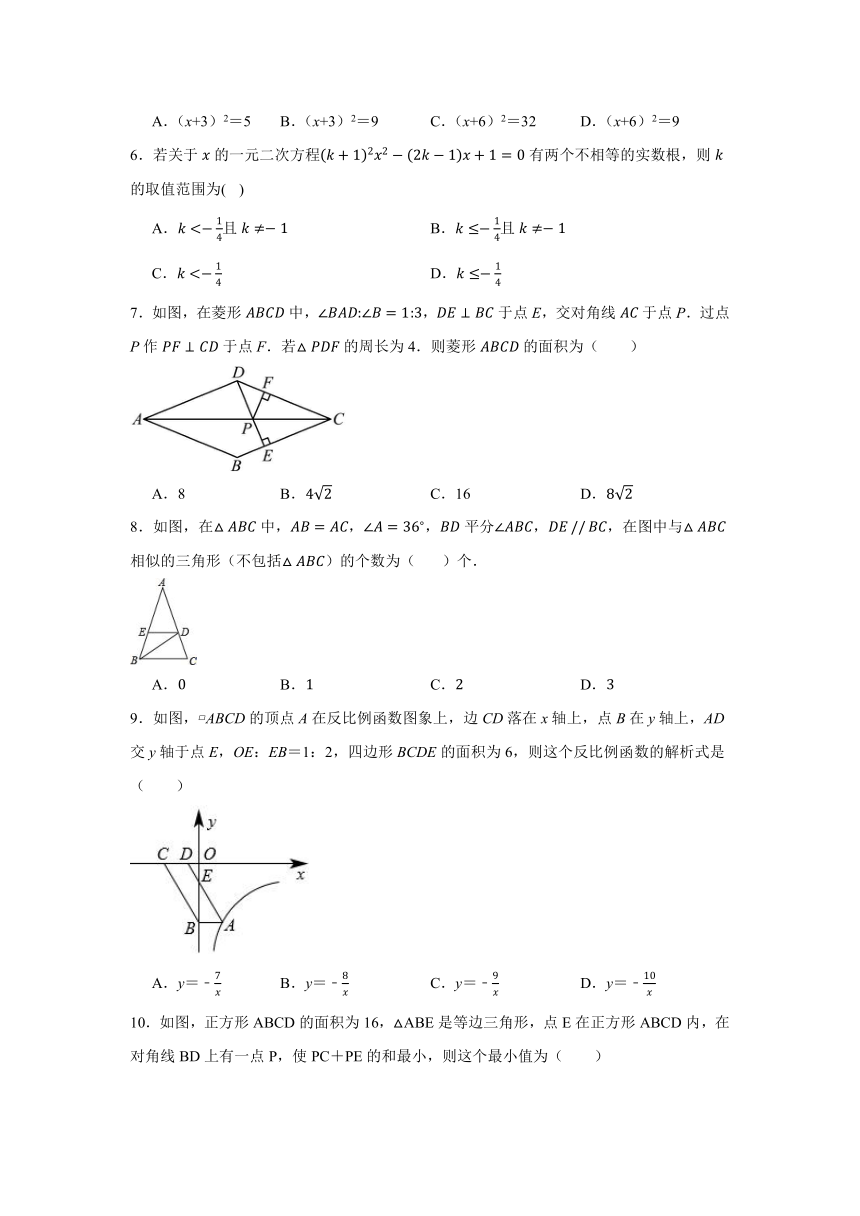
7.如图,在菱形中,,于点E,交对角线于点P.过点P作于点F.若的周长为4.则菱形的面积为( )
A.8 B. C.16 D.
8.如图,在中,,,平分,,在图中与相似的三角形(不包括)的个数为( )个.
A. B. C. D.
9.如图, ABCD的顶点A在反比例函数图象上,边CD落在x轴上,点B在y轴上,AD交y轴于点E,OE:EB=1:2,四边形BCDE的面积为6,则这个反比例函数的解析式是( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
10.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为( )
A.4 B.2 C.2 D.2
二、填空题
11.将方程化成一元二次方程的一般形式为 .
12.已知某几何体的三视图如图所示,根据图中数据求得该几何体的体积为 .
13.如图,在菱形中,对角线、交于点,且,,过A点作垂直,交点,则的值为 .
14.若关于x的一元二次方程的一个实数根是,则m的值为 .
15.如图,点A在反比例函数y的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,的面积为,则k的值为 .
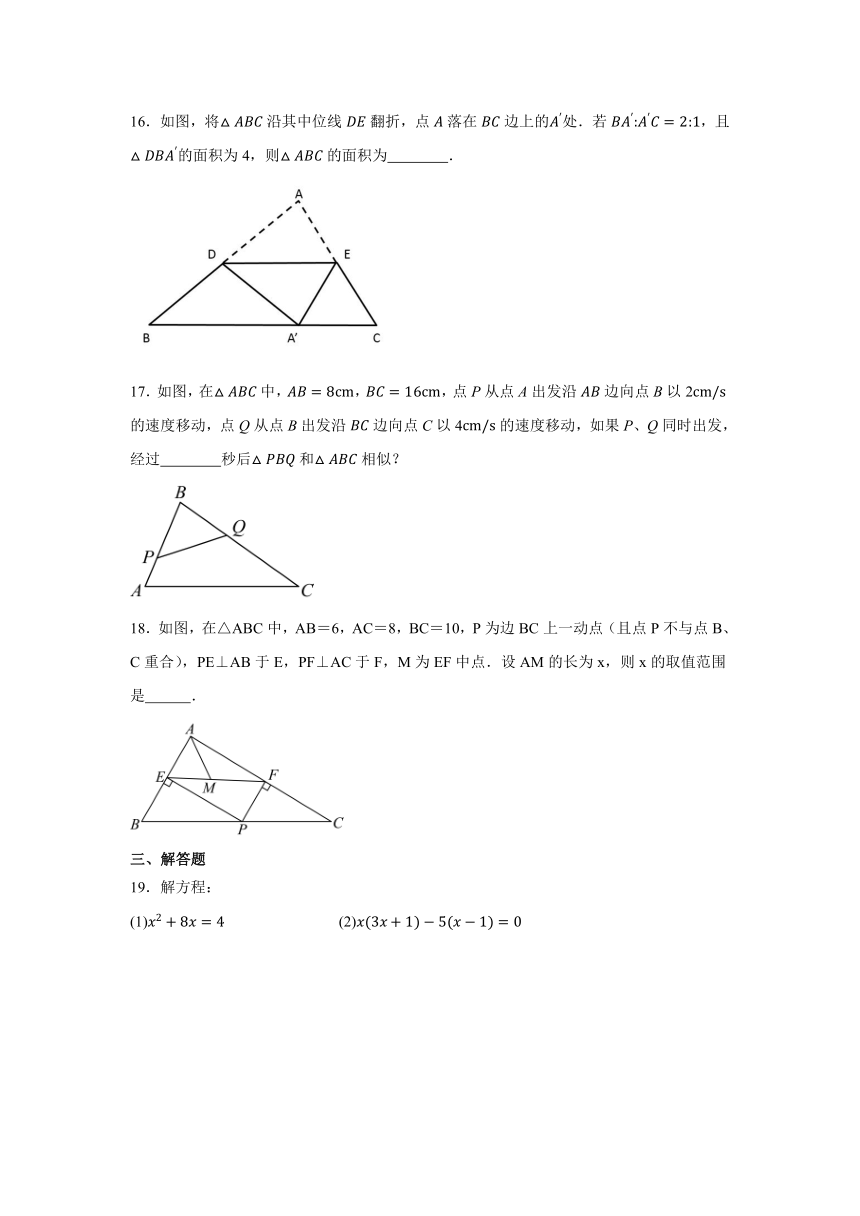
16.如图,将沿其中位线翻折,点落在边上的处.若,且的面积为4,则的面积为 .
17.如图,在中,,,点P从点A出发沿边向点B以2的速度移动,点Q从点B出发沿边向点C以4的速度移动,如果P、Q同时出发,经过 秒后和相似?
18.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是 .
三、解答题
19.解方程:
(1) (2)
20.“石头、剪子、布”是一个广为流传的游戏,规则是:小赵、小张两人都做出“石头”“剪子”“布”3种手势中的1种,其中“石头”赢“剪子”,“剪子”赢“布”,“布”赢“石头”,手势相同不分输赢.假设小赵、小张两人每次都随意并且同时做出3种手势中的1种.
(1)小赵每次做出“石头”手势的概率为________;
(2)用画树状图或列表的方法,求小赵赢的概率.
21.已知关于x的一元二次方程.
(1)求证:此方程有两个不相等的实数根;
(2)设此方程的两个根分别为,,若,求方程的两个根.
22.小明下学途中遇到一棵大树,于是他想利用现有的长度为的小尺测量这棵树的高度.如图,小明笔直站立,把手臂水平向前伸直,将小尺竖直举起,瞄准小尺的两端,,然后不断调整站立的位置,在点处时恰好能看到该大树的顶端和底部.(图中所有点均在同一平面,点,,在同一条直线上.)经测量,小明的手臂长,点到树底端的距离,求大树的高度.
23.如图,直线与双曲线相交于A,B两点,且A,B两点的横坐标分别为1和4.
(1)求,的值;
(2)利用图象,直接写出不等式的解集.
24.销售淡季,某商场积压了一批商品,现欲尽快清仓,决定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.
(1)若要使销售该商品的总利润达到28000元,求x的值;
(2)销售该商品的总利润能否达到30000元 若能,请求出此时的销售单价;若不能,请说明理由.
25.【模型建立】
(1)如图1,在正方形中,,分别是边,上的点,且,探究图中线段,,之间的数量关系.
小明的探究思路如下:延长到点,使,连接,先证明,再证明.
①,,之间的数量关系为________;
②小亮发现这里可以由经过一种图形变换得到,请你写出这种图形变换的过程________.像上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何模型称为半角模型.
【类比探究】
(2)如图2,在四边形中,,与互补,,分别是边,上的点,且,试问线段,,之间具有怎样的数量关系?判断并说明理由.
【模型应用】
(3)如图3,在矩形中,点在边上,,,,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B D A A D C C A
1. B
2. D
3. B
4. D
5. A
6. A
7. D
8. C
9. C
10. A
11.
12..
13.
14.-9
15.
16.12
17.或2
18.2.4≤x<4
19.(1)解:,
配方得:,即,
,
,;
(2)解:,
整理得:,
其中,,,,
,
该方程无解.
20.(1)解:小赵每次做出“石头”手势的概率为;
(2)解:画树状图得:
共有9种等可能的情况数,其中小赵赢的有3种,
则小赵赢的概率是.
21.解:(1)∵△=(4m)2-4×1×(4m2-9)=16m2-16m2+36=36>0,
∴已知关于x的一元二次方程x2-4mx+4m2-9=0一定有两个不相等的实数根;
(2)∵x=2m±3,
∵x1=3 x2,
∴x1+x2=6,
∵x1+x2=4m,
∴4m=6,
∴m=,
∴x=2×±3,
∴x1=6,x2=0.
22.解:.
根据题意,得.点到的距离即,点到的距离即,
∵,
,.
.
.
.
答:大树的高度为.
23.(1)解:根据题意设A,B两点的坐标为,,
∵直线经过A,B两点,
∴,
解得;
(2)解:由图象可知,不等式的解集为或.
24.(1)解:每件商品降价x元后,可售出商品件件,则
解得,
∵尽快清仓,
∴舍去.
答:x的值为15;
(2)
整理得,
,方程没有实数根,所以总利润不能达到30000元.
25.(1)解:①,理由如下:
沿着小明的思路进行证明,
在正方形中,有,,
即有,
,,,
,
,,
,,
,
,
,,
,
,
,,
,结论得证;
②将绕点顺时针旋转即可得到.
理由如下:
在①已经证得,并得到,
,
将绕点顺时针旋转即可得到;
(2),理由如下:
延长至点,使得,连接,如图,
与互补,
,
,
,
,,
,
,,
,
,
,
,
,
,
,,
,
,
,,
,结论得证;
(3)解法一:如图,延长至,使,过作的平行线交的延长线于,延长交于,连接,
四边形是正方形,
,,
,
四边形是平行四边形,
四边形是矩形,
设,则,
,
,
,
,
,
由(1)得:,
在中,由勾股定理得:,
解得:,
,
;
解法二:过点作于点,如图,
,,
在矩形中,,,,
设,则有,
,
在中,,
在中,,
,,
,
,
是等腰直角三角形,
,
,
即:
,,
,
,
,,,
,
,
,
,
结合,解得,
.
姓名:___________班级:___________学号:___________
一、单选题
1.如图所示的立体图形,其主视图是( )
A. B. C. D.
2.对于反比例函数,下列结论错误的是( )
A.函数图象分布在第一、三象限
B.函数图象经过点
C.若点在其图象上,那么点也一定在其图象上
D.若点都在函数图象上,且,则
3.如图是超市的两个摇奖转盘,只有当两个转盘指针同时指在偶数上时才能获一等奖,则摇奖人中一等奖的概率是( )
A. B. C. D.
4.如图,与是位似图形,是位似中心,位似比为,若,则的长为( )
A. B. C. D.
5.将x2+6x+4=0进行配方变形,下列正确的是( )
A.(x+3)2=5 B.(x+3)2=9 C.(x+6)2=32 D.(x+6)2=9
6.若关于的一元二次方程有两个不相等的实数根,则的取值范围为( )
A.且 B.且
C. D.
7.如图,在菱形中,,于点E,交对角线于点P.过点P作于点F.若的周长为4.则菱形的面积为( )
A.8 B. C.16 D.
8.如图,在中,,,平分,,在图中与相似的三角形(不包括)的个数为( )个.
A. B. C. D.
9.如图, ABCD的顶点A在反比例函数图象上,边CD落在x轴上,点B在y轴上,AD交y轴于点E,OE:EB=1:2,四边形BCDE的面积为6,则这个反比例函数的解析式是( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
10.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为( )
A.4 B.2 C.2 D.2
二、填空题
11.将方程化成一元二次方程的一般形式为 .
12.已知某几何体的三视图如图所示,根据图中数据求得该几何体的体积为 .
13.如图,在菱形中,对角线、交于点,且,,过A点作垂直,交点,则的值为 .
14.若关于x的一元二次方程的一个实数根是,则m的值为 .
15.如图,点A在反比例函数y的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,的面积为,则k的值为 .
16.如图,将沿其中位线翻折,点落在边上的处.若,且的面积为4,则的面积为 .
17.如图,在中,,,点P从点A出发沿边向点B以2的速度移动,点Q从点B出发沿边向点C以4的速度移动,如果P、Q同时出发,经过 秒后和相似?
18.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是 .
三、解答题
19.解方程:
(1) (2)
20.“石头、剪子、布”是一个广为流传的游戏,规则是:小赵、小张两人都做出“石头”“剪子”“布”3种手势中的1种,其中“石头”赢“剪子”,“剪子”赢“布”,“布”赢“石头”,手势相同不分输赢.假设小赵、小张两人每次都随意并且同时做出3种手势中的1种.
(1)小赵每次做出“石头”手势的概率为________;
(2)用画树状图或列表的方法,求小赵赢的概率.
21.已知关于x的一元二次方程.
(1)求证:此方程有两个不相等的实数根;
(2)设此方程的两个根分别为,,若,求方程的两个根.
22.小明下学途中遇到一棵大树,于是他想利用现有的长度为的小尺测量这棵树的高度.如图,小明笔直站立,把手臂水平向前伸直,将小尺竖直举起,瞄准小尺的两端,,然后不断调整站立的位置,在点处时恰好能看到该大树的顶端和底部.(图中所有点均在同一平面,点,,在同一条直线上.)经测量,小明的手臂长,点到树底端的距离,求大树的高度.
23.如图,直线与双曲线相交于A,B两点,且A,B两点的横坐标分别为1和4.
(1)求,的值;
(2)利用图象,直接写出不等式的解集.
24.销售淡季,某商场积压了一批商品,现欲尽快清仓,决定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.
(1)若要使销售该商品的总利润达到28000元,求x的值;
(2)销售该商品的总利润能否达到30000元 若能,请求出此时的销售单价;若不能,请说明理由.
25.【模型建立】
(1)如图1,在正方形中,,分别是边,上的点,且,探究图中线段,,之间的数量关系.
小明的探究思路如下:延长到点,使,连接,先证明,再证明.
①,,之间的数量关系为________;
②小亮发现这里可以由经过一种图形变换得到,请你写出这种图形变换的过程________.像上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何模型称为半角模型.
【类比探究】
(2)如图2,在四边形中,,与互补,,分别是边,上的点,且,试问线段,,之间具有怎样的数量关系?判断并说明理由.
【模型应用】
(3)如图3,在矩形中,点在边上,,,,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B D A A D C C A
1. B
2. D
3. B
4. D
5. A
6. A
7. D
8. C
9. C
10. A
11.
12..
13.
14.-9
15.
16.12
17.或2
18.2.4≤x<4
19.(1)解:,
配方得:,即,
,
,;
(2)解:,
整理得:,
其中,,,,
,
该方程无解.
20.(1)解:小赵每次做出“石头”手势的概率为;
(2)解:画树状图得:
共有9种等可能的情况数,其中小赵赢的有3种,
则小赵赢的概率是.
21.解:(1)∵△=(4m)2-4×1×(4m2-9)=16m2-16m2+36=36>0,
∴已知关于x的一元二次方程x2-4mx+4m2-9=0一定有两个不相等的实数根;
(2)∵x=2m±3,
∵x1=3 x2,
∴x1+x2=6,
∵x1+x2=4m,
∴4m=6,
∴m=,
∴x=2×±3,
∴x1=6,x2=0.
22.解:.
根据题意,得.点到的距离即,点到的距离即,
∵,
,.
.
.
.
答:大树的高度为.
23.(1)解:根据题意设A,B两点的坐标为,,
∵直线经过A,B两点,
∴,
解得;
(2)解:由图象可知,不等式的解集为或.
24.(1)解:每件商品降价x元后,可售出商品件件,则
解得,
∵尽快清仓,
∴舍去.
答:x的值为15;
(2)
整理得,
,方程没有实数根,所以总利润不能达到30000元.
25.(1)解:①,理由如下:
沿着小明的思路进行证明,
在正方形中,有,,
即有,
,,,
,
,,
,,
,
,
,,
,
,
,,
,结论得证;
②将绕点顺时针旋转即可得到.
理由如下:
在①已经证得,并得到,
,
将绕点顺时针旋转即可得到;
(2),理由如下:
延长至点,使得,连接,如图,
与互补,
,
,
,
,,
,
,,
,
,
,
,
,
,
,,
,
,
,,
,结论得证;
(3)解法一:如图,延长至,使,过作的平行线交的延长线于,延长交于,连接,
四边形是正方形,
,,
,
四边形是平行四边形,
四边形是矩形,
设,则,
,
,
,
,
,
由(1)得:,
在中,由勾股定理得:,
解得:,
,
;
解法二:过点作于点,如图,
,,
在矩形中,,,,
设,则有,
,
在中,,
在中,,
,,
,
,
是等腰直角三角形,
,
,
即:
,,
,
,
,,,
,
,
,
,
结合,解得,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
