2025高考物理二轮专题复习-增分指导一 数学方法在物理中的应用 课件(共70张PPT)
文档属性
| 名称 | 2025高考物理二轮专题复习-增分指导一 数学方法在物理中的应用 课件(共70张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-01 21:16:34 | ||
图片预览











文档简介
(共70张PPT)
增分指导一 数学方法在物理中的应用
方法1 估算法
方法2 三角函数法
方法3 均值不等式求极值
方法4 二次函数求极值
方法5 数学归纳法、数列的应用
方法6 求导的妙用
应用数学知识处理物理问题的能力具体要求为:
(1)能根据具体的物理问题列出物理量之间的关系,能把有关的物理条件用
数学方程表示出来.
(2)在解决物理问题时,往往需要经过数学推导和求解,或进行数值计算;求得
结果后,有时还要用图像或函数关系把它表示出来;必要时还应对数学运算
的结果做出物理上的结论或解释.
(3)能够运用几何图形、函数图像解决物理问题,要能够对物理规律、状态
和过程在理解的基础上用合适的图像表示出来,会用图像来处理物理问题.
高中物理解题常见的数学思想方法包括估算法、几何法、函数法、比值法、
图解法、极值法、微元法、归纳法、极限分析法、分类讨论法等,经常要
用到的数学知识包括平面几何、函数图像、三角函数、不等式、数列、微
积分初步等.
方法1 估算法
解决此类问题需要了解一些常见的数据,例如:原子直径数量级为
,地球半径约为 ,地球自转周期约为1天(24小时),地球
公转周期约为1年,近地卫星的运行周期约为85分钟,月球绕地球运行周
期约为27天,一个鸡蛋的质量约为,中学生的质量约为 ,课桌的
高度约为,每层楼的高度约为,自行车的速度约为 ,
,地球表面重力加速度约为 ,月球表面重力加速度约为
地球表面的 等.
例1 我国执行火星探测任务的“天问一号”探测器在成功实施三次近火制动
后,进入运行周期约为 的椭圆形停泊轨道,轨道与火星表面的
最近距离约为.已知火星半径约为 ,火星表面处自
由落体的加速度大小约为 ,则“天问一号”的停泊轨道与火星表面
的最远距离约为( )
A. B. C. D.
√
[解析] 已知火星半径,则火星近地卫星的周期为 ,设停泊轨道
的半长轴为,由开普勒第三定律可知,整理得 ,代入数
据得 ,即
,近火点和远火点距离即为长轴,近火点与火星表面
的最近距离约为 ,则远火点与火星表面的最远距离约为
.
技法点拨
对数值计算的处理,第一是得出目标物理量函数关系再计算数值,不要列
一个关系式得出一个中间结果,这样不仅使得计算成本提高,而且容易因
为每一步的四舍五入导致最终的结果出现偏差,把关系式清晰表达出来,
再代入数据,是一种更加科学的计算方式.第二就是要掌握必要的估算技
巧,上述解答过程中,将3.7和4抵消、
而且结果是取在一个区间内,并不需要最终得出精确的数值.
例2 [2024·杭州高级中学模拟] 如图所示是某同学跳远的频闪图,该同学
身高,起跳点为点.图中辅助标线方格横竖长度比为, 取
,则他起跳时的初速度最接近的值是( )
A. B. C. D.
√
[解析] 从图中可知,人的高度约占三格竖直线,所以一格竖直线的长度
约为,则一格水平线的长度约为 ,从
起跳到最高点过程,重心在竖直方向运动了约2格,根据逆向思维有
,,解得, ,水平方向运动了约2
格,则有,解得 ,起跳时的初速度为
,故选D.
方法2 三角函数法
角度1 三角函数求极值
(1) ,当 时, .
(2) ,当时, .
(3)辅助角求极值
三角函数:
,其中 .
当 时,有极大值 .
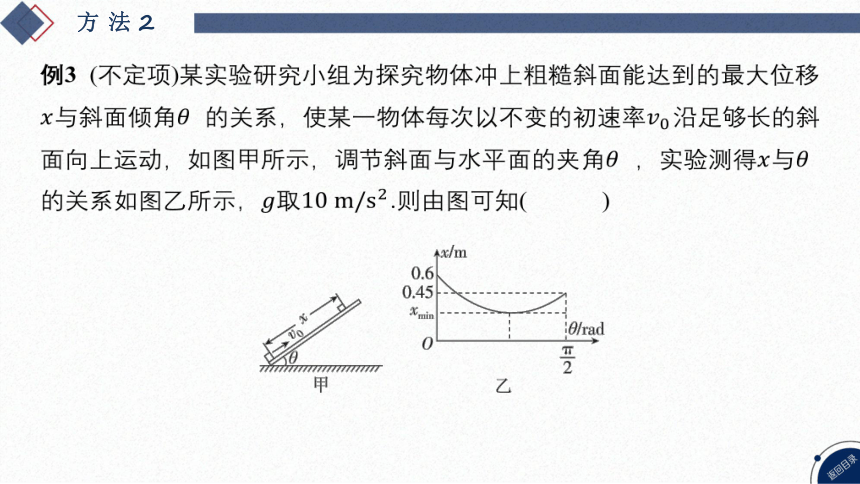
例3 (不定项)某实验研究小组为探究物体冲上粗糙斜面能达到的最大位移
与斜面倾角 的关系,使某一物体每次以不变的初速率 沿足够长的斜
面向上运动,如图甲所示,调节斜面与水平面的夹角 ,实验测得与
的关系如图乙所示,取 .则由图可知( )
A.物体的初速率
B.物体与斜面间的动摩擦因数
C.图乙中
D.取初始位置所在水平面为重力势能参考平面,当 ,物体上滑过
程中动能与重力势能相等时,物体上滑的位移为
√
√
[解析] 由图乙可知,当 时,物体做竖直上抛运动,摩擦力是零,由
竖直上抛运动的速度—位移关系公式可得 ,解得
,A错误;当 时,物体沿水平面做匀
减速直线运动,由动能定理可得 ,解得
,B正确;物体沿斜面向上运动时,由动能定理
可得 ,代入数据整理可得
,C正确;设动能与重力
势能相等时,物体上滑的位移为 ,则有
,代入数据解得
,D错误.
角度2 正、余弦定理的应用
(1)正弦定理
在如图所示的三角形中,各边和所对应角的正弦之比相等,即
.
(2)余弦定理
在如图所示的三角形中,有:
例4 [2024·湖北卷] 如图所示,两拖船、 拉着无
动力货船 一起在静水中沿图中虚线方向匀速前进,
两根水平缆绳与虚线的夹角均保持为 .假设水对
三艘船在水平方向的作用力大小均为 ,方向与船
的运动方向相反,则每艘拖船发动机提供的动力大
小为( )
A. B. C. D.
√
[解析] 对货船受力分析如图甲所示,其中 为绳的拉力,根据正交分解
法可得,对拖船受力分析如图乙所示,其中 为发动机提
供的动力,有 ,根据牛顿第三定律
可知,联立解得 ,故B正确.
例5 一振动片以频率 做简谐运动时,固定在振动片上
的两根细杆同步周期性地触动水面上、 两点,两波源
发出的波在水面上形成稳定的干涉图样. 是水面上的一
点,、、间的距离均为,如图所示.已知除 点外,
A. B. C. D.
在、连线上还有其他振幅极大的点,其中距最近的点到的距离为 .
则该波的波长为( )
√
[解析] 设与点最近的振幅极大点为 ,则
,由余弦定理有
,根据干涉加
强点距离差的关系有 ,则有
,所以波长为 ,选项C正确.
方法3 均值不等式求极值
由均值不等式 可知:
(1)两个正数的积为定值时,若两数相等,和最小;
(2)两个正数的和为定值时,若两数相等,积最大.
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平
面内,一电阻不计,质量为的金属棒 垂直于导轨,并静置
于绝缘固定支架上.边长为的正方形 区域内,存在垂直于
纸面向外的匀强磁场.支架上方的导轨间存在竖直向下的匀强磁
场.两磁场的磁感应强度大小随时间 的变化关系均为
,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为 时,对
施加竖直向上的拉力,恰使其向上做加速度大小为 的匀加
速直线运动,整个运动过程中与两边导轨接触良好.已知
与导轨间的动摩擦因数为 ,重力加速度大小为 . 不计空气阻
力,两磁场互不影响.
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平面内,一电
阻不计,质量为的金属棒 垂直于导轨,并静置于绝缘固定支架上.边
长为的正方形 区域内,存在垂直于纸面向外的匀强磁场.支架上方的
导轨间存在竖直向下的匀强磁场.两磁场的磁感应强度大小随时间 的变
化关系均为,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为时,对 施加竖直
向上的拉力,恰使其向上做加速度大小为 的匀加速直线运动,整个运动
过程中与两边导轨接触良好.已知与导轨间的动摩擦因数为 ,重力
加速度大小为 .不计空气阻力,两磁场互不影响.
(1) 求通过面积的磁通量大小随时间 变化的关系式,以及感应电动
势的大小,并写出 中电流的方向;
[答案] ; ; 从流向
[解析] 通过面积的磁通量大小随时间 变化的关系式为
根据法拉第电磁感应定律得
由楞次定律可知中的电流方向为从流向 .
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平面内,一电
阻不计,质量为的金属棒 垂直于导轨,并静置于绝缘固定支架上.边
长为的正方形 区域内,存在垂直于纸面向外的匀强磁场.支架上方的
导轨间存在竖直向下的匀强磁场.两磁场的磁感应强度大小随时间 的变
化关系均为,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为时,对 施加竖直
向上的拉力,恰使其向上做加速度大小为 的匀加速直线运动,整个运动
过程中与两边导轨接触良好.已知与导轨间的动摩擦因数为 ,重力
加速度大小为 .不计空气阻力,两磁场互不影响.
(2) 求所受安培力的大小随时间 变化的关系式;
[答案]
[解析] 根据左手定则可知 受到的安培力方向垂直于导轨平
面向里,大小为
其中
设金属棒向上运动的位移为,则根据运动学公式有
导轨接入回路的电阻为
由闭合电路欧姆定律得
联立解得所受安培力的大小随时间 变化的关系式为
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平面内,一电
阻不计,质量为的金属棒 垂直于导轨,并静置于绝缘固定支架上.边
长为的正方形 区域内,存在垂直于纸面向外的匀强磁场.支架上方的
导轨间存在竖直向下的匀强磁场.两磁场的磁感应强度大小随时间 的变
化关系均为,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为时,对 施加竖直
向上的拉力,恰使其向上做加速度大小为 的匀加速直线运动,整个运动
过程中与两边导轨接触良好.已知与导轨间的动摩擦因数为 ,重力
加速度大小为 .不计空气阻力,两磁场互不影响.
(3) 经过多长时间,对 所施加的拉力达到最大值?并求此最大值.
[答案] ;
[解析] 由题知时,对 施加竖直向上的拉力,恰使其向
上做加速度大小为的匀加速直线运动,则对 受力分析,由
牛顿第二定律有
其中
联立可得
整理有
根据均值不等式可知,当且仅当 时取
等号, 有
最大值,此时
的最大值为
方法4 二次函数求极值
(1)二次函数:
①当时,有极值(若二次项系数, 有极小值;若
, 有极大值).
②利用一元二次方程判别式求极值.
(2)用判别式 有解可求某量的极值.
例7 [2024·四川成都模拟] 如图所示,一半径为 的光滑绝缘半球面开口
向下,固定在水平面上.整个空间存在磁感应强度为 、方向竖直向下的匀
强磁场.一电荷量为、质量为的小球 在球面上做水平的匀速
圆周运动,圆心为.球心 到该圆周上任一点的连线与竖直方向的夹角为
.若重力加速度为 ,以下说法正确的是( )
A.从上面俯视,小球沿顺时针方向运动
B.球面对小球的弹力大小为
C.小球的速率越大,则小球受到的洛伦兹力越大
D.磁感应强度的大小可能为
√
[解析] 小球受到的洛伦兹力方向水平指向圆心 ,
根据左手定则可知,从上面俯视小球沿逆时针方
向运动,故A错误;小球竖直方向受力平衡,则有
,可得球面对小球的弹力大小为
,故B错误;根据 可知
小球的速率越大,则小球受到的洛伦兹力越大,
故C正确;水平方向根据牛顿第二定律可得
,整
理可得,对于 的一元
二次方程,根据数学知
识可知,需要满足 ,
可得 ,可知
磁感应强度的大小不可能为 ,故D错误.
方法5 数学归纳法、数列的应用
凡涉及数列求解的物理问题都具有过程多、重复性强的特点,但每一个重
复过程均不是与原来完全相同的重复,而是一种变化了的重复.随着物理
过程的重复,某些物理量逐步发生着前后有联系的变化.该类问题求解的
基本思路为:
(1)逐个分析开始的几个物理过程;
(2)利用归纳法从中找出物理量变化的通项公式(这是解题的关键);
(3)最后分析整个物理过程,应用数列特点和规律求解.
无穷数列的求和,一般是无穷递减数列,有相应的公式可用.
等差数列:为公差 .
等比数列:为公比 .
例8 如图所示,水平地面上放有木板
和滑块 ,两者静止在同一直线上,木
板底面光滑, 与地面间的动摩擦因
数为 ,某时刻滑块从左侧以水平初速度滑上木板,已知滑块 与木
板上表面间的动摩擦因数也为 ,滑块、木板的质量均为 ,重力加
速度为 ,
开始时木板与滑块相距 ,木
板足够长,与之间的碰撞均为弹性碰撞,碰撞时间极短,与 发生碰
撞后反弹,之后木板每当运动到与滑块 上次碰撞的位置时,恰好不再
相对 滑动,求:
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为,重力加速度为,开始时木板与滑块 相距
,木板足够长,与 之间的碰撞
均为弹性碰撞,碰撞时间极短,与发生碰撞后反弹,之后木板 每当
运动到与滑块上次碰撞的位置时,恰好不再相对 滑动,求:
(1) 滑上后经多长时间与 发生第1次碰撞;
[答案]
[解析] 假设先与达到共同速度,再与
相碰.设滑上后经时间,木板与滑块
达到共同速度,该过程和 组成的系统
动量守恒,有
解得
设此过程木板的位移为,对 由动能定
理得
解得 ,则假设正确.
此过程对木板 由动量定理有
解得
设再经时间,与 发生第1次碰撞,有
解得
则滑上后到与 发生第1次碰撞经过的
时间为
联立解得 .
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为 ,重力加速
度为,开始时木板与滑块相距 ,
木板足够长,与之间的碰撞均为弹性碰撞,碰撞时间极短,与 发生
碰撞后反弹,之后木板每当运动到与滑块 上次碰撞的位置时,恰好不
再相对 滑动,求:
(2) 滑块 的质量;
[答案]
[解析] 设滑块的质量为,木板与 发生
第1次碰撞后瞬间的速度为,木板 的速
度为,以水平向右为正方向,与 之间
发生弹性碰撞,对、 组成的系统,根据动
量守恒定律和机械能守恒定律,有
根据木板总是在与滑块 上次碰撞的位置恰
好不再与滑块相对滑动,可知从、 碰后
到、再次共速,的位移为0,设、 再
次共速的速度为,该过程时间为 ,由匀
变速直线运动规律有
则
与第1次碰后瞬间到与 相互作用达到共
速过程,、 组成的系统动量守恒,有
联立解得, ,
.
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为,重力加速度为 ,
开始时木板与滑块相距 ,木
板足够长,与之间的碰撞均为弹性碰撞,碰撞时间极短,与 发生碰
撞后反弹,之后木板每当运动到与滑块 上次碰撞的位置时,恰好不再
相对 滑动,求:
(3) 第2次碰撞前,滑块相对木板 滑动的距离;
[答案]
[解析] 设第1次碰撞前相对 滑动的距
离为,对、 组成的系统由能量守
恒定律有
解得
设从第1次碰撞后到第2次碰撞前 相对
滑动的距离为 ,同理有
解得
则第2次碰撞前,滑块相对木板 滑动
的距离 .
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为,重力加速度为,开始时木板与滑块 相
距,木板足够长,与 之间的碰
撞均为弹性碰撞,碰撞时间极短,与发生碰撞后反弹,之后木板 每
当运动到与滑块上次碰撞的位置时,恰好不再相对 滑动,求:
(4) 经次碰撞,滑块 能运动的总位移.
[答案]
[解析] 第1次碰撞后,、 做匀变速运动,
根据牛顿第二定律分别有
解得、的加速度大小,
根据运动学规律有
解得
设回到与第1次碰撞的位置时, 的速度
为
则有
解得,所以第2次碰前 已静止,
由(3)知,此时的速度为
同理,第2次碰后瞬间,、 的速度分别
为,
第3次碰前已静止, 的速度为
第3次碰后瞬间,、 的速度分别为
,
……
依次类推,第次碰后瞬间, 的速度为
设第1次碰后滑块运动的位移为 ,该过
程,对滑块 由动能定理,有
解得
同理,第2次碰后滑块 运动的位移为
第次碰后滑块 运动的位移为
则经次碰撞,滑块 能运动的总位移
根据等比数列求和,可知 .
方法6 求导的妙用
(1)分析物理问题,应用物理规律,将已知量和未知量之间建立一定的函数式;
(2)求导数,代入数据求出物理量;
(3)求物理量最值时,先求导数,再建立导数为零的独立方程,解方程得
出自变量或自变量的表达式,将自变量代入原来的函数式中求出目标量的
最大值或最小值.
例9 [2024·丽水中学模拟] 如图所示,一个带正电的绝缘圆环竖直放置,
圆环半径为,带电荷量为 ,电荷量均匀分布在圆环表面上,将一正试
探电荷 从圆环中心偏右侧一点(图中未画出)的位置由静止释放,试探电
荷只在电场力的作用下沿着中心轴线向右侧运动,则下列说法正确的是
( )
A.试探电荷将向右先加速后减速
B.试探电荷的加速度逐渐减小
C.当试探电荷距离圆环中心为 时,其加速度最大
D.将圆环所带电荷量扩大两倍,则加速度最大的位置
右移
√
[解析] 根据圆环电场分布的对称性可知,圆环中心轴
线上的电场强度均背离圆环中心,沿着中轴线向外,
则可知试探电荷将始终受到向右的电场力,一直做加
速运动,故A错误;如图所示,将圆环上所带电荷进
行无限分割,设每一份的电荷量为,则其在 点的
场强 ,其水平分量
,微元累加并根据对称性可知, 点的合
场强为 ,令
,则其导函数为
,此时 ,
可知当,即试探电荷距离圆环中心为 时,
场强最大,加速度最大,并且这个位置与电荷量无关,
故C正确,B、D错误.
例10 [2024·学军中学模拟] 如图所示,两根平行金属
导轨固定在水平桌面上,每根导轨每米的电阻为
,导轨的端点、 用电阻可以忽
[答案]
略的导线相连,两导轨间的距离 .随时间变化的匀强磁场垂直于
桌面,已知磁感应强度与时间的关系为,比例系数 .
一电阻不计的金属杆可在导轨上无摩擦地滑动,在滑动过程中保持与导轨
垂直,在时刻,金属杆紧靠在、 端,在外力作用下,杆以恒定的
加速度从静止开始向导轨的另一端滑动,求 时金属杆所受的安培
力大小.
[解析] 整个电路中的感应电动势由两部分组成,一部
分是金属杆向左做切割磁感线的运动引起的,称为动
生电动势;另一部分是由于磁感应强度变化所引起的,
称为感生电动势.
设金属杆的加速度为,在时刻 的磁通量
根据法拉第电磁感应定律,电路内产生的感应电动势
为
整个电路的总电阻和总电流分别为
因此,金属杆所受的安培力为
代入题中数据,得
增分指导一 数学方法在物理中的应用
方法1 估算法
方法2 三角函数法
方法3 均值不等式求极值
方法4 二次函数求极值
方法5 数学归纳法、数列的应用
方法6 求导的妙用
应用数学知识处理物理问题的能力具体要求为:
(1)能根据具体的物理问题列出物理量之间的关系,能把有关的物理条件用
数学方程表示出来.
(2)在解决物理问题时,往往需要经过数学推导和求解,或进行数值计算;求得
结果后,有时还要用图像或函数关系把它表示出来;必要时还应对数学运算
的结果做出物理上的结论或解释.
(3)能够运用几何图形、函数图像解决物理问题,要能够对物理规律、状态
和过程在理解的基础上用合适的图像表示出来,会用图像来处理物理问题.
高中物理解题常见的数学思想方法包括估算法、几何法、函数法、比值法、
图解法、极值法、微元法、归纳法、极限分析法、分类讨论法等,经常要
用到的数学知识包括平面几何、函数图像、三角函数、不等式、数列、微
积分初步等.
方法1 估算法
解决此类问题需要了解一些常见的数据,例如:原子直径数量级为
,地球半径约为 ,地球自转周期约为1天(24小时),地球
公转周期约为1年,近地卫星的运行周期约为85分钟,月球绕地球运行周
期约为27天,一个鸡蛋的质量约为,中学生的质量约为 ,课桌的
高度约为,每层楼的高度约为,自行车的速度约为 ,
,地球表面重力加速度约为 ,月球表面重力加速度约为
地球表面的 等.
例1 我国执行火星探测任务的“天问一号”探测器在成功实施三次近火制动
后,进入运行周期约为 的椭圆形停泊轨道,轨道与火星表面的
最近距离约为.已知火星半径约为 ,火星表面处自
由落体的加速度大小约为 ,则“天问一号”的停泊轨道与火星表面
的最远距离约为( )
A. B. C. D.
√
[解析] 已知火星半径,则火星近地卫星的周期为 ,设停泊轨道
的半长轴为,由开普勒第三定律可知,整理得 ,代入数
据得 ,即
,近火点和远火点距离即为长轴,近火点与火星表面
的最近距离约为 ,则远火点与火星表面的最远距离约为
.
技法点拨
对数值计算的处理,第一是得出目标物理量函数关系再计算数值,不要列
一个关系式得出一个中间结果,这样不仅使得计算成本提高,而且容易因
为每一步的四舍五入导致最终的结果出现偏差,把关系式清晰表达出来,
再代入数据,是一种更加科学的计算方式.第二就是要掌握必要的估算技
巧,上述解答过程中,将3.7和4抵消、
而且结果是取在一个区间内,并不需要最终得出精确的数值.
例2 [2024·杭州高级中学模拟] 如图所示是某同学跳远的频闪图,该同学
身高,起跳点为点.图中辅助标线方格横竖长度比为, 取
,则他起跳时的初速度最接近的值是( )
A. B. C. D.
√
[解析] 从图中可知,人的高度约占三格竖直线,所以一格竖直线的长度
约为,则一格水平线的长度约为 ,从
起跳到最高点过程,重心在竖直方向运动了约2格,根据逆向思维有
,,解得, ,水平方向运动了约2
格,则有,解得 ,起跳时的初速度为
,故选D.
方法2 三角函数法
角度1 三角函数求极值
(1) ,当 时, .
(2) ,当时, .
(3)辅助角求极值
三角函数:
,其中 .
当 时,有极大值 .
例3 (不定项)某实验研究小组为探究物体冲上粗糙斜面能达到的最大位移
与斜面倾角 的关系,使某一物体每次以不变的初速率 沿足够长的斜
面向上运动,如图甲所示,调节斜面与水平面的夹角 ,实验测得与
的关系如图乙所示,取 .则由图可知( )
A.物体的初速率
B.物体与斜面间的动摩擦因数
C.图乙中
D.取初始位置所在水平面为重力势能参考平面,当 ,物体上滑过
程中动能与重力势能相等时,物体上滑的位移为
√
√
[解析] 由图乙可知,当 时,物体做竖直上抛运动,摩擦力是零,由
竖直上抛运动的速度—位移关系公式可得 ,解得
,A错误;当 时,物体沿水平面做匀
减速直线运动,由动能定理可得 ,解得
,B正确;物体沿斜面向上运动时,由动能定理
可得 ,代入数据整理可得
,C正确;设动能与重力
势能相等时,物体上滑的位移为 ,则有
,代入数据解得
,D错误.
角度2 正、余弦定理的应用
(1)正弦定理
在如图所示的三角形中,各边和所对应角的正弦之比相等,即
.
(2)余弦定理
在如图所示的三角形中,有:
例4 [2024·湖北卷] 如图所示,两拖船、 拉着无
动力货船 一起在静水中沿图中虚线方向匀速前进,
两根水平缆绳与虚线的夹角均保持为 .假设水对
三艘船在水平方向的作用力大小均为 ,方向与船
的运动方向相反,则每艘拖船发动机提供的动力大
小为( )
A. B. C. D.
√
[解析] 对货船受力分析如图甲所示,其中 为绳的拉力,根据正交分解
法可得,对拖船受力分析如图乙所示,其中 为发动机提
供的动力,有 ,根据牛顿第三定律
可知,联立解得 ,故B正确.
例5 一振动片以频率 做简谐运动时,固定在振动片上
的两根细杆同步周期性地触动水面上、 两点,两波源
发出的波在水面上形成稳定的干涉图样. 是水面上的一
点,、、间的距离均为,如图所示.已知除 点外,
A. B. C. D.
在、连线上还有其他振幅极大的点,其中距最近的点到的距离为 .
则该波的波长为( )
√
[解析] 设与点最近的振幅极大点为 ,则
,由余弦定理有
,根据干涉加
强点距离差的关系有 ,则有
,所以波长为 ,选项C正确.
方法3 均值不等式求极值
由均值不等式 可知:
(1)两个正数的积为定值时,若两数相等,和最小;
(2)两个正数的和为定值时,若两数相等,积最大.
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平
面内,一电阻不计,质量为的金属棒 垂直于导轨,并静置
于绝缘固定支架上.边长为的正方形 区域内,存在垂直于
纸面向外的匀强磁场.支架上方的导轨间存在竖直向下的匀强磁
场.两磁场的磁感应强度大小随时间 的变化关系均为
,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为 时,对
施加竖直向上的拉力,恰使其向上做加速度大小为 的匀加
速直线运动,整个运动过程中与两边导轨接触良好.已知
与导轨间的动摩擦因数为 ,重力加速度大小为 . 不计空气阻
力,两磁场互不影响.
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平面内,一电
阻不计,质量为的金属棒 垂直于导轨,并静置于绝缘固定支架上.边
长为的正方形 区域内,存在垂直于纸面向外的匀强磁场.支架上方的
导轨间存在竖直向下的匀强磁场.两磁场的磁感应强度大小随时间 的变
化关系均为,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为时,对 施加竖直
向上的拉力,恰使其向上做加速度大小为 的匀加速直线运动,整个运动
过程中与两边导轨接触良好.已知与导轨间的动摩擦因数为 ,重力
加速度大小为 .不计空气阻力,两磁场互不影响.
(1) 求通过面积的磁通量大小随时间 变化的关系式,以及感应电动
势的大小,并写出 中电流的方向;
[答案] ; ; 从流向
[解析] 通过面积的磁通量大小随时间 变化的关系式为
根据法拉第电磁感应定律得
由楞次定律可知中的电流方向为从流向 .
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平面内,一电
阻不计,质量为的金属棒 垂直于导轨,并静置于绝缘固定支架上.边
长为的正方形 区域内,存在垂直于纸面向外的匀强磁场.支架上方的
导轨间存在竖直向下的匀强磁场.两磁场的磁感应强度大小随时间 的变
化关系均为,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为时,对 施加竖直
向上的拉力,恰使其向上做加速度大小为 的匀加速直线运动,整个运动
过程中与两边导轨接触良好.已知与导轨间的动摩擦因数为 ,重力
加速度大小为 .不计空气阻力,两磁场互不影响.
(2) 求所受安培力的大小随时间 变化的关系式;
[答案]
[解析] 根据左手定则可知 受到的安培力方向垂直于导轨平
面向里,大小为
其中
设金属棒向上运动的位移为,则根据运动学公式有
导轨接入回路的电阻为
由闭合电路欧姆定律得
联立解得所受安培力的大小随时间 变化的关系式为
例6 [2024·安徽卷] 如图所示,一“ ”形金属导轨固定在竖直平面内,一电
阻不计,质量为的金属棒 垂直于导轨,并静置于绝缘固定支架上.边
长为的正方形 区域内,存在垂直于纸面向外的匀强磁场.支架上方的
导轨间存在竖直向下的匀强磁场.两磁场的磁感应强度大小随时间 的变
化关系均为,为常数 .支架上方的导轨足够长,两边导
轨单位长度的电阻均为,下方导轨的总电阻为时,对 施加竖直
向上的拉力,恰使其向上做加速度大小为 的匀加速直线运动,整个运动
过程中与两边导轨接触良好.已知与导轨间的动摩擦因数为 ,重力
加速度大小为 .不计空气阻力,两磁场互不影响.
(3) 经过多长时间,对 所施加的拉力达到最大值?并求此最大值.
[答案] ;
[解析] 由题知时,对 施加竖直向上的拉力,恰使其向
上做加速度大小为的匀加速直线运动,则对 受力分析,由
牛顿第二定律有
其中
联立可得
整理有
根据均值不等式可知,当且仅当 时取
等号, 有
最大值,此时
的最大值为
方法4 二次函数求极值
(1)二次函数:
①当时,有极值(若二次项系数, 有极小值;若
, 有极大值).
②利用一元二次方程判别式求极值.
(2)用判别式 有解可求某量的极值.
例7 [2024·四川成都模拟] 如图所示,一半径为 的光滑绝缘半球面开口
向下,固定在水平面上.整个空间存在磁感应强度为 、方向竖直向下的匀
强磁场.一电荷量为、质量为的小球 在球面上做水平的匀速
圆周运动,圆心为.球心 到该圆周上任一点的连线与竖直方向的夹角为
.若重力加速度为 ,以下说法正确的是( )
A.从上面俯视,小球沿顺时针方向运动
B.球面对小球的弹力大小为
C.小球的速率越大,则小球受到的洛伦兹力越大
D.磁感应强度的大小可能为
√
[解析] 小球受到的洛伦兹力方向水平指向圆心 ,
根据左手定则可知,从上面俯视小球沿逆时针方
向运动,故A错误;小球竖直方向受力平衡,则有
,可得球面对小球的弹力大小为
,故B错误;根据 可知
小球的速率越大,则小球受到的洛伦兹力越大,
故C正确;水平方向根据牛顿第二定律可得
,整
理可得,对于 的一元
二次方程,根据数学知
识可知,需要满足 ,
可得 ,可知
磁感应强度的大小不可能为 ,故D错误.
方法5 数学归纳法、数列的应用
凡涉及数列求解的物理问题都具有过程多、重复性强的特点,但每一个重
复过程均不是与原来完全相同的重复,而是一种变化了的重复.随着物理
过程的重复,某些物理量逐步发生着前后有联系的变化.该类问题求解的
基本思路为:
(1)逐个分析开始的几个物理过程;
(2)利用归纳法从中找出物理量变化的通项公式(这是解题的关键);
(3)最后分析整个物理过程,应用数列特点和规律求解.
无穷数列的求和,一般是无穷递减数列,有相应的公式可用.
等差数列:为公差 .
等比数列:为公比 .
例8 如图所示,水平地面上放有木板
和滑块 ,两者静止在同一直线上,木
板底面光滑, 与地面间的动摩擦因
数为 ,某时刻滑块从左侧以水平初速度滑上木板,已知滑块 与木
板上表面间的动摩擦因数也为 ,滑块、木板的质量均为 ,重力加
速度为 ,
开始时木板与滑块相距 ,木
板足够长,与之间的碰撞均为弹性碰撞,碰撞时间极短,与 发生碰
撞后反弹,之后木板每当运动到与滑块 上次碰撞的位置时,恰好不再
相对 滑动,求:
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为,重力加速度为,开始时木板与滑块 相距
,木板足够长,与 之间的碰撞
均为弹性碰撞,碰撞时间极短,与发生碰撞后反弹,之后木板 每当
运动到与滑块上次碰撞的位置时,恰好不再相对 滑动,求:
(1) 滑上后经多长时间与 发生第1次碰撞;
[答案]
[解析] 假设先与达到共同速度,再与
相碰.设滑上后经时间,木板与滑块
达到共同速度,该过程和 组成的系统
动量守恒,有
解得
设此过程木板的位移为,对 由动能定
理得
解得 ,则假设正确.
此过程对木板 由动量定理有
解得
设再经时间,与 发生第1次碰撞,有
解得
则滑上后到与 发生第1次碰撞经过的
时间为
联立解得 .
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为 ,重力加速
度为,开始时木板与滑块相距 ,
木板足够长,与之间的碰撞均为弹性碰撞,碰撞时间极短,与 发生
碰撞后反弹,之后木板每当运动到与滑块 上次碰撞的位置时,恰好不
再相对 滑动,求:
(2) 滑块 的质量;
[答案]
[解析] 设滑块的质量为,木板与 发生
第1次碰撞后瞬间的速度为,木板 的速
度为,以水平向右为正方向,与 之间
发生弹性碰撞,对、 组成的系统,根据动
量守恒定律和机械能守恒定律,有
根据木板总是在与滑块 上次碰撞的位置恰
好不再与滑块相对滑动,可知从、 碰后
到、再次共速,的位移为0,设、 再
次共速的速度为,该过程时间为 ,由匀
变速直线运动规律有
则
与第1次碰后瞬间到与 相互作用达到共
速过程,、 组成的系统动量守恒,有
联立解得, ,
.
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为,重力加速度为 ,
开始时木板与滑块相距 ,木
板足够长,与之间的碰撞均为弹性碰撞,碰撞时间极短,与 发生碰
撞后反弹,之后木板每当运动到与滑块 上次碰撞的位置时,恰好不再
相对 滑动,求:
(3) 第2次碰撞前,滑块相对木板 滑动的距离;
[答案]
[解析] 设第1次碰撞前相对 滑动的距
离为,对、 组成的系统由能量守
恒定律有
解得
设从第1次碰撞后到第2次碰撞前 相对
滑动的距离为 ,同理有
解得
则第2次碰撞前,滑块相对木板 滑动
的距离 .
例8 如图所示,水平地面上放有木板和滑块 ,两者静止在同一直线上,
木板底面光滑,与地面间的动摩擦因数为 ,某时刻滑块 从左侧以水
平初速度滑上木板,已知滑块与木板上表面间的动摩擦因数也为 ,
滑块、木板的质量均为,重力加速度为,开始时木板与滑块 相
距,木板足够长,与 之间的碰
撞均为弹性碰撞,碰撞时间极短,与发生碰撞后反弹,之后木板 每
当运动到与滑块上次碰撞的位置时,恰好不再相对 滑动,求:
(4) 经次碰撞,滑块 能运动的总位移.
[答案]
[解析] 第1次碰撞后,、 做匀变速运动,
根据牛顿第二定律分别有
解得、的加速度大小,
根据运动学规律有
解得
设回到与第1次碰撞的位置时, 的速度
为
则有
解得,所以第2次碰前 已静止,
由(3)知,此时的速度为
同理,第2次碰后瞬间,、 的速度分别
为,
第3次碰前已静止, 的速度为
第3次碰后瞬间,、 的速度分别为
,
……
依次类推,第次碰后瞬间, 的速度为
设第1次碰后滑块运动的位移为 ,该过
程,对滑块 由动能定理,有
解得
同理,第2次碰后滑块 运动的位移为
第次碰后滑块 运动的位移为
则经次碰撞,滑块 能运动的总位移
根据等比数列求和,可知 .
方法6 求导的妙用
(1)分析物理问题,应用物理规律,将已知量和未知量之间建立一定的函数式;
(2)求导数,代入数据求出物理量;
(3)求物理量最值时,先求导数,再建立导数为零的独立方程,解方程得
出自变量或自变量的表达式,将自变量代入原来的函数式中求出目标量的
最大值或最小值.
例9 [2024·丽水中学模拟] 如图所示,一个带正电的绝缘圆环竖直放置,
圆环半径为,带电荷量为 ,电荷量均匀分布在圆环表面上,将一正试
探电荷 从圆环中心偏右侧一点(图中未画出)的位置由静止释放,试探电
荷只在电场力的作用下沿着中心轴线向右侧运动,则下列说法正确的是
( )
A.试探电荷将向右先加速后减速
B.试探电荷的加速度逐渐减小
C.当试探电荷距离圆环中心为 时,其加速度最大
D.将圆环所带电荷量扩大两倍,则加速度最大的位置
右移
√
[解析] 根据圆环电场分布的对称性可知,圆环中心轴
线上的电场强度均背离圆环中心,沿着中轴线向外,
则可知试探电荷将始终受到向右的电场力,一直做加
速运动,故A错误;如图所示,将圆环上所带电荷进
行无限分割,设每一份的电荷量为,则其在 点的
场强 ,其水平分量
,微元累加并根据对称性可知, 点的合
场强为 ,令
,则其导函数为
,此时 ,
可知当,即试探电荷距离圆环中心为 时,
场强最大,加速度最大,并且这个位置与电荷量无关,
故C正确,B、D错误.
例10 [2024·学军中学模拟] 如图所示,两根平行金属
导轨固定在水平桌面上,每根导轨每米的电阻为
,导轨的端点、 用电阻可以忽
[答案]
略的导线相连,两导轨间的距离 .随时间变化的匀强磁场垂直于
桌面,已知磁感应强度与时间的关系为,比例系数 .
一电阻不计的金属杆可在导轨上无摩擦地滑动,在滑动过程中保持与导轨
垂直,在时刻,金属杆紧靠在、 端,在外力作用下,杆以恒定的
加速度从静止开始向导轨的另一端滑动,求 时金属杆所受的安培
力大小.
[解析] 整个电路中的感应电动势由两部分组成,一部
分是金属杆向左做切割磁感线的运动引起的,称为动
生电动势;另一部分是由于磁感应强度变化所引起的,
称为感生电动势.
设金属杆的加速度为,在时刻 的磁通量
根据法拉第电磁感应定律,电路内产生的感应电动势
为
整个电路的总电阻和总电流分别为
因此,金属杆所受的安培力为
代入题中数据,得
同课章节目录
