2025浙江高考物理一轮复习-“17~20解答”限时练12(含解析)
文档属性
| 名称 | 2025浙江高考物理一轮复习-“17~20解答”限时练12(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-02 00:00:00 | ||
图片预览


文档简介
2025浙江高考物理一轮复习-“17~20解答”限时练12
17.(8分)[2024·余姚中学模拟] 某同学喝一盒牛奶但未喝完,想测量剩余牛奶的体积.他发现插在牛奶盒里的透明竖直吸管内残留了一小段长度为l的牛奶柱,于是用蜡将接口密封,吸管下端在液面上方,如图所示.他先在室内测得牛奶盒接口处到牛奶柱下端的距离为l1,再将牛奶盒拿到室外一段时间后,测得接口处到牛奶柱下端的距离变为l2.已知室内的热力学温度为T1,室外的热力学温度为T2,大气压恒为p0,吸管横截面积为S,牛奶盒容积为V0,牛奶密度为ρ,重力加速度为g,忽略吸管壁的厚度和牛奶柱的蒸发,整个过程牛奶盒未形变,牛奶未溢出,牛奶盒及吸管内的封闭气体视为理想气体.
(1)求剩余牛奶的体积;
(2)若气体的内能与热力学温度成正比,比例系数为k,求该过程封闭气体吸收的热量.
18.(11分)如图所示,一质量为m=1 kg可看成质点的滑块以初速度v0=2 m/s,从P点与水平方向成θ=37°抛出后,恰能从a点沿ab方向切入粗糙斜面轨道,斜面ab轨道长为xab=10 m,斜面ab与半径R=1.25 m的竖直光滑圆弧轨道相切于b点,O点为圆弧的圆心,c点为圆弧的最低点且位于O点正下方,圆弧圆心角θ=37°.c点靠近水平传送带左侧,传送带cd间距离为L=3.4 m,以v=5 m/s的恒定速度顺时针转动,传送带与光滑圆弧、光滑水平面均保持平滑对接,水平面上有2个位于同一直线上、处于静止状态的相同小球,每个小球质量m0=2 kg.滑块与小球、小球与小球之间发生的都是弹性正碰,滑块与斜面及传送带间的动摩擦因数μ=0.5,重力加速度g取10 m/s2.不计一切空气阻力,求:
(1)滑块从P点抛出落到a点所需要的运动时间t0;
(2)滑块滑到圆弧轨道的最低点c时对轨道的压力大小;
(3)滑块第一次向右通过传送带的过程中,摩擦力对滑块的冲量大小;
(4)2个小球最终获得的总动能.
19.(11分)[2024·绍兴模拟] 某国产品牌的电动汽车配备了基于电容器的制动能量回收系统,它有效的增加了电动汽车的续航里程.其工作原理为踩下驱动踏板时电池给电动机供电,松开驱动踏板或踩下刹车时发电机工作回收能量.为进一步研究,某兴趣小组设计了如图甲所示的模型:右侧为直流发电机模型,在磁极与圆柱形铁芯之间形成辐射状的磁场,导线框的经过处的磁感应强度大小均为B,方向始终与两条边的运动方向垂直,剖面图如图乙所示.导线框的ab、dc边延长段可在两金属半圆A、D内侧自由转动,且接触良好.金属半圆环D左侧接一单刀双掷开关:踩下驱动踏板,开关接通1,电池给导线框供电,导线框相当于电动机,所用电池的电动势为E,内阻为r;松开驱动踏板或踩下刹车,开关自动切换接通2,导线框相当于发电机,给电容器充电,所接电容器的电容为C.导线框与圆柱形铁芯中心轴线重合,ab、dc边长度均为L,两边间距离为d.导线框的ab、dc边质量均为m,其余部分导线质量不计,导线框的总电阻为R.初始时电容器不带电、导线框静止,电路其余部分的电阻不计,两金属半圆环和两磁极间的空隙忽略不计.
(1)求踩下驱动踏板后,导线框刚启动时的电流I和ab边受到的安培力的大小F;
(2)求踩下驱动踏板后,导线框可达到的最大角速度ωm;
(3)求从踩下踏板到导线框角速度最大的过程中导线框上产生的焦耳热;
(4)当导线框达到最大转动速度后松开驱动踏板,在一段时间后导线框将匀速转动,求此时电容器C上的带电荷量q及储存的电场能W.(提示:可根据电容器充电过程中电荷克服电场力做功与电势能转化关系并结合U-q图像求解)
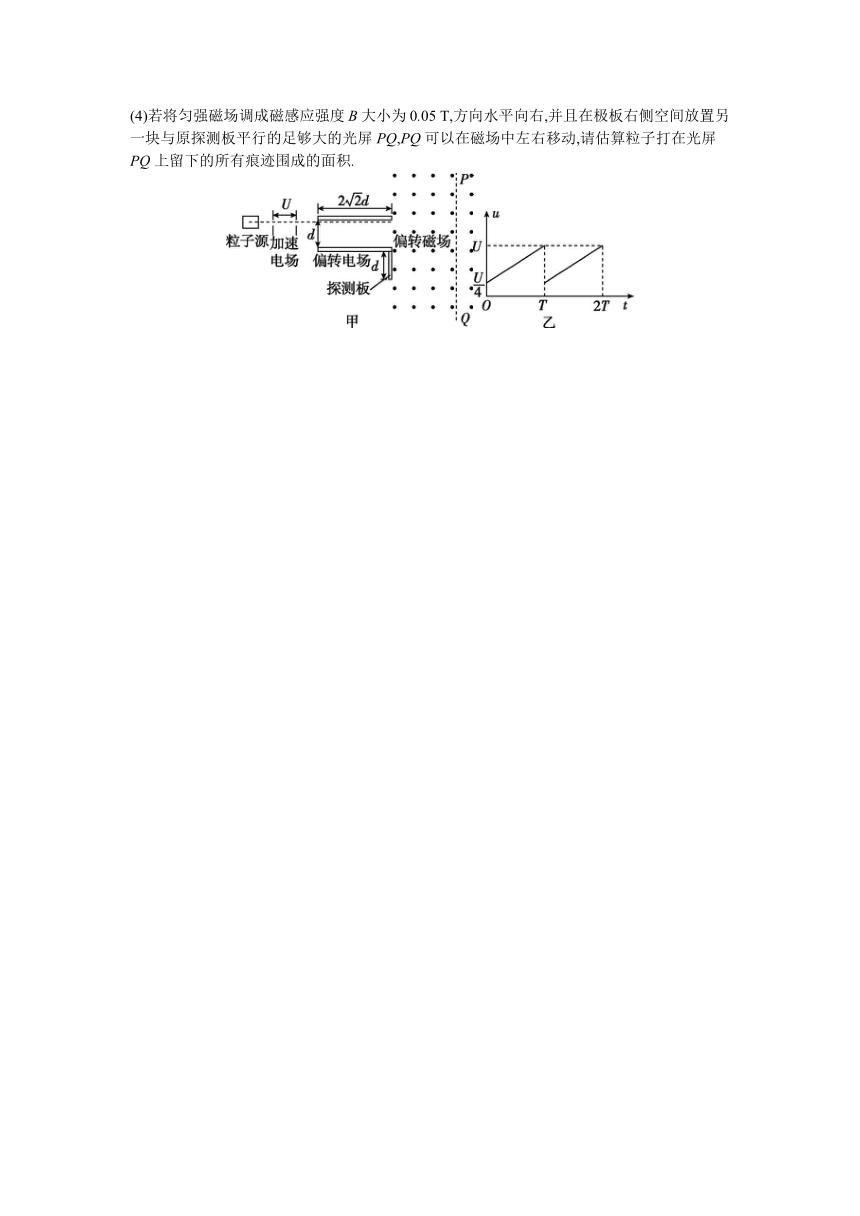
20.(11分)[2024·宁波模拟] 粒子偏转装置是研究高能物理的重要仪器,主要由加速电场,偏转电场和偏转磁场三部分构成.如图甲所示为某科研团队设计的粒子偏转装置示意图,粒子源可以均匀连续的产生质量为m,电荷量为q的带正电粒子,其比荷=1×108 C/kg,初速度可忽略不计.带电粒子经电压U=100 V的加速电场加速后,贴近上板边缘,水平飞入两平行金属板中的偏转电场.两水平金属板间距为d=0.02 m,板长为2d,板间加有图乙所示的周期性变化的电压,其最大电压也为U、最小电压为,周期远大于粒子在偏转电场中运动的时间(忽略粒子穿越偏转电场时电压的变化),下极板右端正下方紧挨金属板竖直放置长度为d的探测板.若带电粒子能由偏转电场飞出,则飞出后立即进入平行板右侧的垂直纸面向外的水平匀强磁场,最后经匀强磁场偏转后打在探测板上;若不能飞出偏转电场,则被金属板吸收并导走.不计带电粒子的重力和粒子间的相互作用力.
(1)求从偏转电场出射的粒子通过偏转电场的时间t;
(2)求一个周期T内,从偏转电场出射的粒子数占粒子源全部发射粒子数的百分比η;
(3)求从偏转电场出射的粒子全部能够到达探测板时,磁感应强度B需要满足的条件;
(4)若将匀强磁场调成磁感应强度B大小为0.05 T,方向水平向右,并且在极板右侧空间放置另一块与原探测板平行的足够大的光屏PQ,PQ可以在磁场中左右移动,请估算粒子打在光屏PQ上留下的所有痕迹围成的面积.
参考答案与详细解析
17.(1)V0- (2)(p0+ρgl)(l2-l1)S+kT2-kT1
[解析] (1)设室内牛奶盒内空气体积V,将牛奶盒拿到室外为等压变化,根据= (1分)
得V= (1分)
剩余牛奶的体积V剩=V0-V=V0- (1分)
(2)牛奶盒在室内时封闭气体的内能U1=kT1
牛奶盒在室外时封闭气体的内能U2=kT2
内能变化量ΔU=U2-U1=kT2-kT1 (2分)
该过程气体对外界做功
W=-(p0+ρgl)(l2-l1)S (1分)
根据ΔU=W+Q (1分)
该过程封闭气体吸收的热量
Q=(p0+ρgl)(l2-l1)S+kT2-kT1 (1分)
18.(1)0.24 s (2)49.2 N
(3)2 N·s (4) J
[解析] (1)滑块从P点抛出时竖直方向的分速度
vy=v0sin θ (1分)
滑块从P点抛出落到a点所需要的运动时间
t0==0.24 s(1分)
(2)根据动能定理有
mgxabsin θ+mgR(1-cos θ)-μmgxabcos θ=m-m (1分)
解得vc=7 m/s
在c点,根据牛顿第二定律可得
FNc-mg=
FNc=49.2 N(1分)
根据牛顿第三定律可得滑块滑到圆弧轨道的最低点c时对轨道的压力大小
FNc'=FNc=49.2 N(1分)
(3)滑块在传送带上的加速度
a=μg=5 m/s2
滑块速度与传送带速度相等的所需的时间
t1==0.4 s
此过程滑块的位移
x1==2.4 m所以滑块在传送带上先匀减速后匀速,匀速阶段滑块与传送带间没有摩擦力,滑块第一次向右通过传送带的过程中,摩擦力对滑块的冲量大小
I=μmgt1=2 N·s(1分)
(4)滑块第一次与小球发生弹性碰撞,根据动量守恒定律和能量守恒定律可得
mv=mv1+m0u1
mv2=m+m0
解得v1=-v,u1=v (2分)
由于小球质量相等均为m0,且发生的都是弹性碰撞,他们之间将进行速度交换,分析可知,物块第一次返回还没到传送带左端速度就减小为零,接下来将再次返回做匀加速运动,直到速度增加到v1,再与小球1发生弹性碰撞.同理可得,第二次碰撞后,物块和小球的速度大小分别为
v2=v1=-v
u2=v× (1分)
则2个小球的总动能为
Ek=m0(+)= J(1分)
19.(1) (2)
(3)
(4)
[解析] (1)由闭合电路欧姆定律,可得I= (1分)
ab边受到的安培力的大小为F=BIL= (1分)
(2)依题意,有I= (1分)
当I=0时,转速达到最大,可得vm=,ωm= (1分)
(3)对导线框ab、dc应用动量定理,可得2BLt=2mvm(1分)
通过电路的电荷量为q=t= (1分)
导线框产生的焦耳热为
Q=Eq-(2m)()= (1分)
(4)导线框从最大速度减至v时稳定,对该过程应用动量定理有
-2BLt=2mv-2mvm(1分)
电路中流过的电荷量为q=t
此时电容器所带电荷量为q=2BLvC
解得q= (1分)
如图作U-q图像,由微元法可知图像下面积等于电容器储存的电能
W=Uq= (1分)
联立,解得W= (1分)
20.(1)4×10-7 s (2)33.3%
(3) T≤B≤ T
(4)×10-4 m2
[解析] (1)在加速电场中,根据动能定理qU=m-0 (1分)
解得进入偏转电场的初速度为v0=×105 m/s
粒子在偏转电场中的运动,如图所示
穿过偏转电场时,水平方向做匀速直线运动,有2d=v0t
解得从偏转电场出射的粒子通过偏转电场的时间为t==4×10-7 s(1分)
(2)粒子恰好从下极板右端飞出时,根据类平抛运动的规律,有
2d=v0t、d=at2、a=
解得U0==50 V(1分)
所以一个周期T内,从偏转电场出射的粒子数占粒子源全部发射粒子数的百分比为η=×100%=33.3%(1分)
(3)设粒子飞入磁场时的速度为v,在磁场中做匀速圆周运动,根据洛伦兹力提供向心力,有qvB=m (1分)
设粒子飞入磁场时,其速度与水平方向的夹角为θ,则有vcos θ=v0
设粒子进入磁场后,y方向偏移的位移为Δy,由几何关系可知Δy=2rcos θ
解得Δy=,与速度v无关 (1分)
设粒子在偏转电场中的最小偏移量为ymin,则有ymin=t2=
若偏转电场出射的粒子全部能够到达探测板,需满足≤Δy≤d
解得≤B≤
因此从偏转电场出射的粒子全部能够到达探测板时,磁感应强度B需要满足的条件为 T≤B≤ T(1分)
(4)由洛伦兹力提供向心力,有qvyB=m
解得r==,tan θ== (1分)
联立代入数据解得r==y (2分)
粒子打在光屏PQ上留下的所有痕迹如图所示
当U1=U,ymin==0.01 m时,有rmin=0.01 m
当U2=U0,ymax=d=0.02 m时,有rmax=0.02 m
所以粒子打在光屏PQ上留下的所有痕迹围成的面积为
S=π+π+(-)=+3×10-4 m2 (1分)
17.(8分)[2024·余姚中学模拟] 某同学喝一盒牛奶但未喝完,想测量剩余牛奶的体积.他发现插在牛奶盒里的透明竖直吸管内残留了一小段长度为l的牛奶柱,于是用蜡将接口密封,吸管下端在液面上方,如图所示.他先在室内测得牛奶盒接口处到牛奶柱下端的距离为l1,再将牛奶盒拿到室外一段时间后,测得接口处到牛奶柱下端的距离变为l2.已知室内的热力学温度为T1,室外的热力学温度为T2,大气压恒为p0,吸管横截面积为S,牛奶盒容积为V0,牛奶密度为ρ,重力加速度为g,忽略吸管壁的厚度和牛奶柱的蒸发,整个过程牛奶盒未形变,牛奶未溢出,牛奶盒及吸管内的封闭气体视为理想气体.
(1)求剩余牛奶的体积;
(2)若气体的内能与热力学温度成正比,比例系数为k,求该过程封闭气体吸收的热量.
18.(11分)如图所示,一质量为m=1 kg可看成质点的滑块以初速度v0=2 m/s,从P点与水平方向成θ=37°抛出后,恰能从a点沿ab方向切入粗糙斜面轨道,斜面ab轨道长为xab=10 m,斜面ab与半径R=1.25 m的竖直光滑圆弧轨道相切于b点,O点为圆弧的圆心,c点为圆弧的最低点且位于O点正下方,圆弧圆心角θ=37°.c点靠近水平传送带左侧,传送带cd间距离为L=3.4 m,以v=5 m/s的恒定速度顺时针转动,传送带与光滑圆弧、光滑水平面均保持平滑对接,水平面上有2个位于同一直线上、处于静止状态的相同小球,每个小球质量m0=2 kg.滑块与小球、小球与小球之间发生的都是弹性正碰,滑块与斜面及传送带间的动摩擦因数μ=0.5,重力加速度g取10 m/s2.不计一切空气阻力,求:
(1)滑块从P点抛出落到a点所需要的运动时间t0;
(2)滑块滑到圆弧轨道的最低点c时对轨道的压力大小;
(3)滑块第一次向右通过传送带的过程中,摩擦力对滑块的冲量大小;
(4)2个小球最终获得的总动能.
19.(11分)[2024·绍兴模拟] 某国产品牌的电动汽车配备了基于电容器的制动能量回收系统,它有效的增加了电动汽车的续航里程.其工作原理为踩下驱动踏板时电池给电动机供电,松开驱动踏板或踩下刹车时发电机工作回收能量.为进一步研究,某兴趣小组设计了如图甲所示的模型:右侧为直流发电机模型,在磁极与圆柱形铁芯之间形成辐射状的磁场,导线框的经过处的磁感应强度大小均为B,方向始终与两条边的运动方向垂直,剖面图如图乙所示.导线框的ab、dc边延长段可在两金属半圆A、D内侧自由转动,且接触良好.金属半圆环D左侧接一单刀双掷开关:踩下驱动踏板,开关接通1,电池给导线框供电,导线框相当于电动机,所用电池的电动势为E,内阻为r;松开驱动踏板或踩下刹车,开关自动切换接通2,导线框相当于发电机,给电容器充电,所接电容器的电容为C.导线框与圆柱形铁芯中心轴线重合,ab、dc边长度均为L,两边间距离为d.导线框的ab、dc边质量均为m,其余部分导线质量不计,导线框的总电阻为R.初始时电容器不带电、导线框静止,电路其余部分的电阻不计,两金属半圆环和两磁极间的空隙忽略不计.
(1)求踩下驱动踏板后,导线框刚启动时的电流I和ab边受到的安培力的大小F;
(2)求踩下驱动踏板后,导线框可达到的最大角速度ωm;
(3)求从踩下踏板到导线框角速度最大的过程中导线框上产生的焦耳热;
(4)当导线框达到最大转动速度后松开驱动踏板,在一段时间后导线框将匀速转动,求此时电容器C上的带电荷量q及储存的电场能W.(提示:可根据电容器充电过程中电荷克服电场力做功与电势能转化关系并结合U-q图像求解)
20.(11分)[2024·宁波模拟] 粒子偏转装置是研究高能物理的重要仪器,主要由加速电场,偏转电场和偏转磁场三部分构成.如图甲所示为某科研团队设计的粒子偏转装置示意图,粒子源可以均匀连续的产生质量为m,电荷量为q的带正电粒子,其比荷=1×108 C/kg,初速度可忽略不计.带电粒子经电压U=100 V的加速电场加速后,贴近上板边缘,水平飞入两平行金属板中的偏转电场.两水平金属板间距为d=0.02 m,板长为2d,板间加有图乙所示的周期性变化的电压,其最大电压也为U、最小电压为,周期远大于粒子在偏转电场中运动的时间(忽略粒子穿越偏转电场时电压的变化),下极板右端正下方紧挨金属板竖直放置长度为d的探测板.若带电粒子能由偏转电场飞出,则飞出后立即进入平行板右侧的垂直纸面向外的水平匀强磁场,最后经匀强磁场偏转后打在探测板上;若不能飞出偏转电场,则被金属板吸收并导走.不计带电粒子的重力和粒子间的相互作用力.
(1)求从偏转电场出射的粒子通过偏转电场的时间t;
(2)求一个周期T内,从偏转电场出射的粒子数占粒子源全部发射粒子数的百分比η;
(3)求从偏转电场出射的粒子全部能够到达探测板时,磁感应强度B需要满足的条件;
(4)若将匀强磁场调成磁感应强度B大小为0.05 T,方向水平向右,并且在极板右侧空间放置另一块与原探测板平行的足够大的光屏PQ,PQ可以在磁场中左右移动,请估算粒子打在光屏PQ上留下的所有痕迹围成的面积.
参考答案与详细解析
17.(1)V0- (2)(p0+ρgl)(l2-l1)S+kT2-kT1
[解析] (1)设室内牛奶盒内空气体积V,将牛奶盒拿到室外为等压变化,根据= (1分)
得V= (1分)
剩余牛奶的体积V剩=V0-V=V0- (1分)
(2)牛奶盒在室内时封闭气体的内能U1=kT1
牛奶盒在室外时封闭气体的内能U2=kT2
内能变化量ΔU=U2-U1=kT2-kT1 (2分)
该过程气体对外界做功
W=-(p0+ρgl)(l2-l1)S (1分)
根据ΔU=W+Q (1分)
该过程封闭气体吸收的热量
Q=(p0+ρgl)(l2-l1)S+kT2-kT1 (1分)
18.(1)0.24 s (2)49.2 N
(3)2 N·s (4) J
[解析] (1)滑块从P点抛出时竖直方向的分速度
vy=v0sin θ (1分)
滑块从P点抛出落到a点所需要的运动时间
t0==0.24 s(1分)
(2)根据动能定理有
mgxabsin θ+mgR(1-cos θ)-μmgxabcos θ=m-m (1分)
解得vc=7 m/s
在c点,根据牛顿第二定律可得
FNc-mg=
FNc=49.2 N(1分)
根据牛顿第三定律可得滑块滑到圆弧轨道的最低点c时对轨道的压力大小
FNc'=FNc=49.2 N(1分)
(3)滑块在传送带上的加速度
a=μg=5 m/s2
滑块速度与传送带速度相等的所需的时间
t1==0.4 s
此过程滑块的位移
x1==2.4 m
I=μmgt1=2 N·s(1分)
(4)滑块第一次与小球发生弹性碰撞,根据动量守恒定律和能量守恒定律可得
mv=mv1+m0u1
mv2=m+m0
解得v1=-v,u1=v (2分)
由于小球质量相等均为m0,且发生的都是弹性碰撞,他们之间将进行速度交换,分析可知,物块第一次返回还没到传送带左端速度就减小为零,接下来将再次返回做匀加速运动,直到速度增加到v1,再与小球1发生弹性碰撞.同理可得,第二次碰撞后,物块和小球的速度大小分别为
v2=v1=-v
u2=v× (1分)
则2个小球的总动能为
Ek=m0(+)= J(1分)
19.(1) (2)
(3)
(4)
[解析] (1)由闭合电路欧姆定律,可得I= (1分)
ab边受到的安培力的大小为F=BIL= (1分)
(2)依题意,有I= (1分)
当I=0时,转速达到最大,可得vm=,ωm= (1分)
(3)对导线框ab、dc应用动量定理,可得2BLt=2mvm(1分)
通过电路的电荷量为q=t= (1分)
导线框产生的焦耳热为
Q=Eq-(2m)()= (1分)
(4)导线框从最大速度减至v时稳定,对该过程应用动量定理有
-2BLt=2mv-2mvm(1分)
电路中流过的电荷量为q=t
此时电容器所带电荷量为q=2BLvC
解得q= (1分)
如图作U-q图像,由微元法可知图像下面积等于电容器储存的电能
W=Uq= (1分)
联立,解得W= (1分)
20.(1)4×10-7 s (2)33.3%
(3) T≤B≤ T
(4)×10-4 m2
[解析] (1)在加速电场中,根据动能定理qU=m-0 (1分)
解得进入偏转电场的初速度为v0=×105 m/s
粒子在偏转电场中的运动,如图所示
穿过偏转电场时,水平方向做匀速直线运动,有2d=v0t
解得从偏转电场出射的粒子通过偏转电场的时间为t==4×10-7 s(1分)
(2)粒子恰好从下极板右端飞出时,根据类平抛运动的规律,有
2d=v0t、d=at2、a=
解得U0==50 V(1分)
所以一个周期T内,从偏转电场出射的粒子数占粒子源全部发射粒子数的百分比为η=×100%=33.3%(1分)
(3)设粒子飞入磁场时的速度为v,在磁场中做匀速圆周运动,根据洛伦兹力提供向心力,有qvB=m (1分)
设粒子飞入磁场时,其速度与水平方向的夹角为θ,则有vcos θ=v0
设粒子进入磁场后,y方向偏移的位移为Δy,由几何关系可知Δy=2rcos θ
解得Δy=,与速度v无关 (1分)
设粒子在偏转电场中的最小偏移量为ymin,则有ymin=t2=
若偏转电场出射的粒子全部能够到达探测板,需满足≤Δy≤d
解得≤B≤
因此从偏转电场出射的粒子全部能够到达探测板时,磁感应强度B需要满足的条件为 T≤B≤ T(1分)
(4)由洛伦兹力提供向心力,有qvyB=m
解得r==,tan θ== (1分)
联立代入数据解得r==y (2分)
粒子打在光屏PQ上留下的所有痕迹如图所示
当U1=U,ymin==0.01 m时,有rmin=0.01 m
当U2=U0,ymax=d=0.02 m时,有rmax=0.02 m
所以粒子打在光屏PQ上留下的所有痕迹围成的面积为
S=π+π+(-)=+3×10-4 m2 (1分)
同课章节目录
